गणित Chapter 5 समांतर श्रेणी
Sponsor Area
NCERT Solution For Class 10 गणित गणित
निम्नलिखित स्थितियों में से किन स्थितियों में संबद्ध संख्याओं की सूचि A.P. है और क्यों?
प्रत्येक किलो मीटर के बाद का टैक्सी का किराया, जबकि प्रथम किलो मीटर के लिए किराया 15 रु. है और प्रत्येक अतिरिक्त किलो मीटर के लिए किराया 8 रु. है।
पहले किमी. का किराया = 15 रु. = a1
दूसरे किमी. का किराया = 15 + 8 = 23 रु. = a2
तीसरे किमी. का किराया = 23 + 8 = 31 रु. = a3
चौथे किमी. का किराया = 31 + 8 = 39 रु. = a4
a2 – a1 = 23 – 15 = 8
a3 – a2 = 31 – 23 = 8
a4 – a3 = 39 – 31 = 8
इस प्रकार बानी संख्यायों की सूचि : 15, 23, 31, ... जो की एक A.P. बनाती है जिसमें प्रत्येक अगला पद उससे पिछले पद में 8 जोड़ने से प्राप्त होता है।
निम्नलिखित स्थितिओं में से किन स्थितियों में संबद्ध संख्याओं की सूचि A.P. है और क्यों?
किसी बेलन में उपस्थित हवा की मात्रा, जबकि वायु निकलने वाला पंप प्रत्येक बार बेलन की शेष हवा का 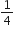 भाग बाहर निकाल देता है।
भाग बाहर निकाल देता है।
माना सिलिंडर में वायु का आयतन = 1l
प्रत्येक बार पंप बची हुई वायु का 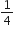 भाग निकाल देता है।
भाग निकाल देता है।
बानी संख्याओं की सूचि है: 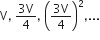 जो कि एक A.P. नहीं है।
जो कि एक A.P. नहीं है।
निम्नलिखित स्थितिओं में से किन स्थितियों में संबद्ध संख्याओं की सूचि A.P. है और क्यों?
प्रत्येक मीटर की खुदाई के बाद, एक कुआँ खोदने में आई लागत, जबकि प्रथम मीटर कुआँ खोदने में आई लागत 150 रु. है और बाद में प्रत्येक मीटर खुदाई की लागत 50 रु. बढ़ती जाती है।
कुआँ खोदने के लिए पहले मीटर का खर्च = 150 रु. = a1
कुआँ खोदने के लिए दूसरे मीटर का खर्च = 150 + 50 = 200 रु. = a2
कुआँ खोदने के लिए तीसरे मीटर का खर्च = 200 + 50 = 250 रु. = a3
कुआँ खोदने के लिए चौथे मीटर का खर्च = 250 + 50 = 300 रु. = a4
सार्व-अन्तर:
a2 – a4 = 200 - 150 = 50 रु.
a3 – a2 = 250 - 200 = 50 रु.
a4 – a3 = 300 - 250 = 50 रु.
अत: बानी संख्यों की सूची: 150, 200, 250, 300, ... जो कि एक A.P. है जिसका प्रथम पद 150 है और सार्व-अन्तर 50 है।
निम्नलिखित स्थितिओं में से किन स्थितियों में संबद्ध संख्याओं की सूचि A.P. है और क्यों?
खाते में प्रत्येक वर्ष का मिश्रधन, जबकि 10000 रु. की राशि 8% वार्षिक की दर से चक्रवृद्धि ब्याज पर जमा की जाती है।
r = 8% वार्षिक
खाते में एक वर्ष बाद राशि = 10000
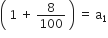
खाते में दो वर्ष बाद राशि = 10000
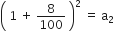
खाते में तीन वर्ष बाद राशि = 10000
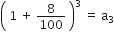
खाते में चार वर्ष बाद राशि = 10000
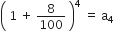
सार्व-अन्तर,
a2 - a1 = 10000
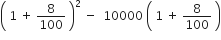
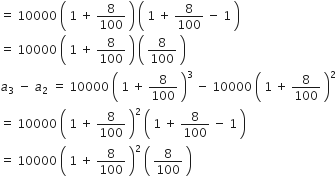
 बराबर नहीं है इसलिए यह A.P. में नहीं है।
बराबर नहीं है इसलिए यह A.P. में नहीं है।दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = 10, d = 10
a = 10, d = 10
पहला पद = a = 10
दूसरा पद = 18 + d = 10+ 10 = 20
तीसरा पद = 20 + d = 20 + 10 = 30
चौथा पद = 30 + d = 30 + 10 = 40
अत: अभीष्ट A.P. है: 10, 20, 30, 40, ...
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = – 2, d = 0
a = –2, d = 0
पहला पद = a = – 2
दूसरा पद = –2 + d = –2 + 0 = –2
तीसरा पद = –2 + d = –2 + 0 = –2
चौथा पद = –2 + d = –2 + 0 = –2
अत: अभीष्ट A.P. है: -2, -2, -2, -2
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = 4, d = – 3
a = 4, d = –3
पहला पद = a = 4
दूसरा पद = 4 + d = 4 + (–3) = 1
तीसरा पद = 1 + d = 1 + (–3) = –2
चौथा पद = –2 + d = –2 + (–3) = –5
अत: अभीष्ट A.P. है: 4, 1, -2, -5
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = – 1, d = 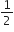
a = – 1, d = 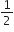
पहला पद = a = -1
दूसरा पद 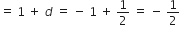
तीसरा पद 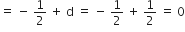
चौथा पद 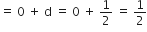
अत: अभीष्ट A.P. है: 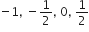
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = – 1.25, d = – 0.25
a = –1.25, d = –0.25
पहला पद = a = –1.25
दूसरा पद = –1.25 + d
= – 1.25 + (–0.25)
= –1.50
तीसरा पद = – 1.50 + d
= – 1.50 + (–0.25)
= – 1.75
चौथा पद = – 1.75 + d
= – 1.75 + (–0.25)
= –2.00
अत: अभीष्ट A.P. है: -1.25, -0.50, -1.75, -2.00, ...
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए:
3, 1, – 1, – 3, ...
3, 1, -1, -3
प्रथम पद, a1 = 3
सार्व अंतर, d = 1 - 3 = -2n
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए:
– 5, – 1, 3, 7, ...
–5, –1, 3, 7, ...
प्रथम पद, a1 = –5
सार्व अंतर d = –1 – (–5) = –1 + 5 = 4
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए: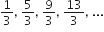
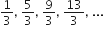
प्रथम पद, a1 = 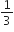
सार्व अंतर d = 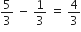
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए:
0.6, 1.7, 2.8, 3.9, ...
0.6, 1.7, 2.8, 3.9, ...
प्रथम पद, a1 = 0.6
सार्व अंतर, d = 1.7 - 0.6 = 1.1
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
2, 4, 8, 16, ...
2, 4, 8, 16, ...
a2 - a1 = 4 - 2 = 2
a3 - a2 = 8 - 4 = 4
a4 - a3 = 16 - 8 = 8
a2 - a1 ![]() a3 - a2
a3 - a2
दी गई संख्याओं की सूची एक A.P. नहीं हैं।
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।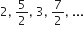
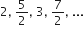
a2 - a1 =
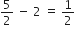
a3 - a2 =
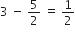
a4 - a3 =
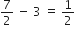
सार्व अंतर, d =
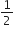
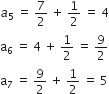
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
– 1.2, – 3.2, – 5.2, – 7.2, ...
–1.2, –3.2, –5.2, –7.2
a2 – a1 = –3.2 – (–1.2)
= –3.2 + 1.2
= –2.0
a3 – a2 = –5.2 – (–3.2)
= –5.2 + 3.2
= –2.0
a4 – a3
= –7.2 – (–5.2)
= –7.2 + 5.2
= –2.0
सार्व अंतर, d = – 2.0
अगले तीन पद:
a5 = – 7.2 + (–2.0) = –9.2
a6 = –9.2 + (–2.0) = –11.2
a7 = –11.2 + (–2.0) = –13.2
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
–10, –6, –2, 2, ...
–10, –6, –2, 2, ...
a2 – a1 = – 6 – (–10)
= –6 + 10 = 4
a3 – a2 = –2 – (–6)
= –2 + 6 = 4
a4 – a3 = 2 – (–2)
= 2 + 2 = 4
सार्व अंतर, d = 4
अगले तीन पद:
a5 = 2 + 4 = 6
a6 = 6 + 4= 10
a7 = 10 + 4 = 14
Sponsor Area
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।

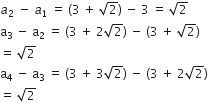

अगले तीन पद:
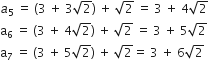
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
0.2, 0.22, 0.222, 0.2222, ...
0.2, 0.22, 0.222, 0.2222, ...
a2 – a1 = 0.22 – 0.2 = 0.02
a3 – a2 = 0.222 – 0.22 = 0.002
a2 – a1 ≠ a3 – a2
दी गई संख्याओं की सूची एक A.P. नहीं हैं।
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
0, – 4, – 8, –12, ...
0, –4, –8, –12, ...
a2 – a1 = –4 – 0 = –4
a3 – a2 = – 8 – (–4)
= – 8 + 4 = –4
a4 – a3 = –12 – (–8) = –12 + 8 = –4
सार्व अंतर, d = –4
अगले तीन पद:
a5 = – 12 + (–4) = –12 – 4 = –16
a6 = – 16 + (–4) = –16 – 4 = –20
a7 = – 20 + (–4) = –20 – 4 = –24
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।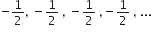
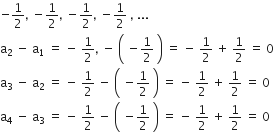
सार्व अंतर, d = 0
अगले तीन पद:
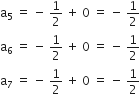
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
1, 3, 9, 27, ...
1, 3, 9, 27, ...
a2 – a1 = 3 – 1 = 2
a3 – a2 = 9 – 3 = 6
a2 – a1 ≠ a3 – a2
दी गई संख्याओं की सूची एक A.P. नहीं हैं।
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
a, 2a, 3a, 4a, ...
a, 2a, 3a, 4a, ...
a2 – a1 = 2a – a = a
a3 – a2 = 3a – 2a = a
a4 – a3 = 4a – 3a = a
सार्व अंतर, d = a
अगले तीन पद:
a5 = 4a + a = 5a
a6 = 5a + a = 6a
a7 = 6a + a = 7a
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
a, a2, a3, a4, ...
a, a2, a3, a4, ...
a2 – a1 = a2 – a = a(a – 1)
a3 – a2 = a3 – a2 = a2 (a – 1)
a2 – a1 ≠ a3 – a2
दी गई संख्याओं की सूची एक A.P. नहीं हैं।
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।

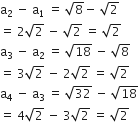
सार्व अंतर, d =
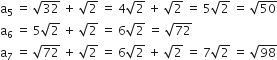
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
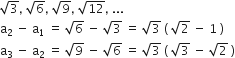
a2 – a1 ≠ a3 – a2
दी गई संख्याओं की सूची एक A.P. नहीं हैं।
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
12, 32, 52, 72, ...
a2 – a1 = 32 – 12 = 9 – 1 = 8
a3 – a2 = 52 – 32 = 25 – 9 = 16
a2 – a1 ≠ a3 – a2
दी गई संख्याओं की सूची एक A.P. नहीं हैं।
निम्नलिखित में से कौन-कौन A.P. हैं? यदि कोई A.P. है, तो इसका सार्व अंतर ज्ञात कीजिए और इनके तीन और पद लिखिए।
12, 52, 72, 73, ...
12, 52, 72, 73, ...
a2 - a1 = 52 – 12 = (5 – 1) (5 + 1)
= (4) (6) = 24
a3 – a2 = 72 – 52 = (7 – 5) (7 + 5)
= (2) (12) = 24
a4 – a3 = 73 – 72 = 73 – 49 = 24
सार्व अंतर, d = 24
अगले तीन पद:
a5 = 73 + 24 = 97
a6 = 97 + 24 = 121
a7 = 121 + 24 = 145
निम्नलिखित सारणी में, रिक्त स्थानों को भरिए, जहाँ A.P. का प्रथम पद a, सर्व अंतर d और nवाँ पद है:
| a | b | c | d | |
| (i) | 7 | 3 | 8 | ... |
| (ii) | -18 | ... | 10 | 0 |
| (iii) | ... | -3 | 10 | -5 |
| (iv) | -18.9 | 2.5 | ... | 3.6 |
| (v) | 3.5 | 0 | 105 | ... |
an = a + (n - 1)d
⇒ an = 7 + (8 - 1)3
⇒ an = 7 + 21
⇒ an = 28
(ii) an = a + (n - 1)d
⇒ 0 = -18 + (10 - 1)d
⇒ 18 = 9d
⇒ 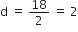
(iii) an = a + (n - 1)d
⇒ -5 = a + (18 - 1)(-3)
⇒ -5 = a - 51
⇒ a = 51 - 5
⇒ a = 46
(iv) an = a + (n - 1)d
⇒ 3.6 = -18.9 + (n - 1)(2.5)
⇒ 3.6 + 18.9 = (n - 1)(2.5)
⇒ 22.5 = (n - 1)(2.5)
⇒ 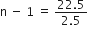
⇒ n - 1 = 9
⇒ n = 9 + 1
⇒ n = 10
(v) an = a + (n - 1)d
⇒ an = 3.5 + (105 - 1)0
⇒ an = 3.5
निम्नलिखित में सही उत्तर चुनिए और औचित्य दीजिए:
A.P. 10, 7, 4, ... का 30वाँ पद है:
-
97
-
77
-
-77
-
-87
C.
-77
A. P. 10, 7, 4, ...
a = 10
d = 7 - 10 = -3
n = 30
an = a + (n - 1) d
a30 = 10 + (30 - 1) (-3)![]() a30 = 10 - 87
a30 = 10 - 87![]() a30 = -77
a30 = -77
तो सही उत्तर है (C) = - 77
निम्नलिखित में सही उत्तर चुनिए और उसका औचित्य दीजिए।
A.P. 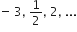 का 11वाँ पद है:
का 11वाँ पद है:
-
28
-
22
-
-38
-
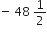
B.
22
A. P. 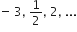
यहाँ, a = - 3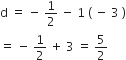
n = 11
an = a + (n - 1) d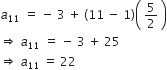
सही उत्तर है = (B) 22
निम्नलिखित समांतर श्रेढियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए:
A.P. का माना सार्व अंतर = d
तीसरा पद = 2 + d + d= 2 + 2d
प्रश्नानुसार,
2 + 2d = 26 2d = 26 - 2
2d = 26 - 2 2d = 24
2d = 24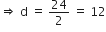
तो, दूसरा पद = 2 + d = 2 + 12 = 14
निम्नलिखित समांतर श्रेढियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए:
माना A.P. का प्रथम पद a है और सार्व अंतर d है।
दूसरा पद = 13
⇒ a + (2 – 1) d = 13
⇒ a + d = 13 ...(i)
चौथा पद = 3
⇒ a+ (4 – 1)d = 3
⇒ a + 3d = 3 ...(ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर
2d = -10
d = -5
तो, a = 18
तो,
तीसरा पद = a + (3 – 1)d
= a + 2d
= 18 + 2 ( – 5 )
= 18 – 10 = 8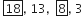
निम्नलिखित समांतर श्रेढियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए:
a = 5
चौथा पद =
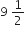
 5 + (4 - 1) d =
5 + (4 - 1) d = 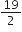
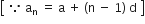
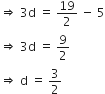
इसलिए,
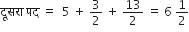
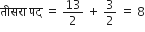
निम्नलिखित समांतर श्रेढियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए:
माना A.P. का सार्व अंतर = d
a = - 4
6वाँ पद = 6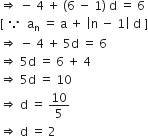
इसलिए,
दूसरा पद = - 4 + 2 = - 2
तीसरा पद = - 2 + 2 = 0
चौथा पद = 0 + 2 = 2
पाँचवाँ = 2 + 2 = 4
निम्नलिखित समांतर श्रेढियों में, रिक्त खानों (boxes) के पदों को ज्ञात कीजिए:
माना A.P. का प्रथम पद a है और सार्व अंतर d है।
दूसरा पद = 38
⇒ a + (2 – 1)d = 38
[ ∴ an = a + (n – 1) d ]
⇒ a + d = 38 ...(i)
⇒ 6वाँ पद = – 22
⇒ a + (6 – 1 )d = – 22
⇒ a + 5d = – 22 ...(ii)
समीकरण (i) और (ii) को हल करने पर
a = 53 d = – 15
इसलिए,
तीसरा पद = 53 + (3 – 1 (– 5))
[ ∵ an = a + (n – 1) d ] = 53 – 30 = 23
चौथा पद = 53 + (4 – 1) (– 15)
[ ∵ an = a + (n – 1) d ] = 8
पाँचवाँ पद = 53 + (5 – 1) (– 15)
[ ∵ = a + (n – 1) d ] = – 7
A.p. : 3, 8, 13, 18, ... का कौन सा पद 78 है?
A. P. : 3, 8, 13, 18, ...
यहाँ, a = 3
d = 8 - 3 = 5
nवाँ पद = 78
तब, an = a + (n - 1)d 78 = 3 + (n - 1) (5)
78 = 3 + (n - 1) (5)
⇒ 5(n - 1) = 78 - 3
⇒ 5 (n - 1) = 75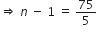
⇒ n - 1 = 15
⇒ n = 15 + 1
⇒ n = 16
अत: A.P. का 16वाँ पद 78 है।
निम्नलिखित समांतर श्रेढियों में से प्रत्येक में कितने पद हैं?
7, 13, 19, ... , 205
7, 13, 19, ... , 205
यहाँ, a = 7
d = 13 - 7 = 6
an = 205
माना पदों की संख्या = n
तब, an = 205![]() a + ( n - 1) d = 205
a + ( n - 1) d = 205![]() 7 + ( n - 1)6 = 205
7 + ( n - 1)6 = 205![]() 6(n - 1) = 205 - 7
6(n - 1) = 205 - 7![]() 6(n - 1) = 198
6(n - 1) = 198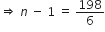
![]() n - 1 = 33
n - 1 = 33![]() n = 33 + 1
n = 33 + 1![]() n = 34
n = 34
अत: दी हुई A.P. में 34 पद हैं।
निम्नलिखित समांतर श्रेढियों में से प्रत्येक में कितने पद हैं?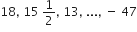
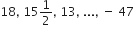
यहाँ, a= 18
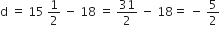
माना पदों की संख्या = n
तब, an = - 47
![<pre>uncaught exception: <b>mkdir(): Permission denied (errno: 2) in /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php at line #56mkdir(): Permission denied</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php line 56<br />#0 [internal function]: _hx_error_handler(2, 'mkdir(): Permis...', '/home/config_ad...', 56, Array)
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/util/sys/Store.class.php(56): mkdir('/home/config_ad...', 493)
#2 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/FolderTreeStorageAndCache.class.php(110): com_wiris_util_sys_Store->mkdirs()
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/RenderImpl.class.php(231): com_wiris_plugin_impl_FolderTreeStorageAndCache->codeDigest('mml=<math xmlns...')
#4 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(59): com_wiris_plugin_impl_RenderImpl->computeDigest(NULL, Array)
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#6 {main}</pre>](/application/zrc/images/qvar/MAEN10042593-3.png) a + (n - 1)d = - 47
a + (n - 1)d = - 47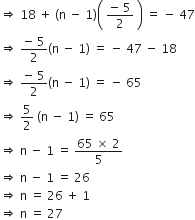
अत: दी हुई A.P. में 27 पद हैं।
Sponsor Area
क्या A.P. 11, 8, 5, 2, ... का एक पद - 150 है? क्यों?
11, 8, 5, 2, ...
a2 – a1 = 8 – 11 = – 3
a3 – a2 = 5 – 8 = – 3
a4 – a3 = 2 – 5 = – 3
an + 1 - an समान हैं, इसलिए दी हुई श्रेढ़ी A.P. है।
अब, a1 = 11
d = - 3
मान (- 150) दी हुई A.P. का nवाँ पद है।
तब, an = - 150![]() a + (n - 1)d = - 150
a + (n - 1)d = - 150![]() 11 + (n - 1) (- 3) = - 150
11 + (n - 1) (- 3) = - 150![]() - 3(n - 1 ) = - 150 - 11
- 3(n - 1 ) = - 150 - 11![]() - 3(n - 1) = -161
- 3(n - 1) = -161![]() - 3(n - 1) = - 161
- 3(n - 1) = - 161![]() 3(n - 1) = 161
3(n - 1) = 161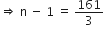
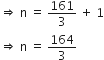
परन्तु n एक धन पूर्णांक होना चाहिए। इसलिए, हमारी कल्पना गलत है, अत: (- 150) दी गई A.P. का एक पद नहीं है।
उस A.P. का 31वाँ पद ज्ञात कीजिए, जिसका 11वाँ पद 38 है और 16वाँ पद 73 है।
यहाँ, a11 = 38, a16 = 38
a11 = a + 10d = 38 ... (i)
a16 = a + 15d = 73 ... (ii)
समीकरण (ii) में से समीकरण (i) घटाने पर
5d = 35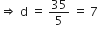
d का मान समीकरण (i) में रखने पर
a + 10 x 7 = 38
a = 38 - 70 = - 32
an = a + (n - 1)d
a31 = a + (31 - 1)d
a31 = - 32 + 30 x 7
a31 = - 32 + 210
a31 = 178
एक A.P. में 50 पद हैं, जिसका तीसरा पद 12 है और अंतिम पद 106 है। इसका 29वाँ पद ज्ञात कीजिए।
a3 = 12
an = 106, n = 50
a3 = a + 2d = 12 ... (i)
an = a + (n - 1)d = 106
⇒ a + (50 - 1)d = 106
⇒ a + 49d = 106 ... (ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर
47d = 106 - 12 = 94
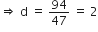
d का मान समीकरण (i) में रखने पर
a + 2 x 2 = 12
⇒ a = 12 - 4 = 8
a29 = a + (29 - 1)d
a29 = 8 + 28 x 2
a29 = 8 + 56 = 64
यदि किसी A.P. के तीसरे और नौवें पद क्रमश: 4 और - 8 हैं तो इसका कौन-सा पद शून्य होगा?
यहाँ, a3 = 4
a9 = - 8
माना nवाँ पद शून्य है
a3 = a + 2d = 4 ... (i)
a9 = a + 8d = - 8 ... (ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर
6d = - 8 - 4 = - 12
⇒ d = 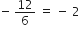
d का मान समीकरण (i) में रखने पर
a + 2 x ( -2 ) = 4
⇒ a1 = 4 + 4 = 8
an = a1 + (n - 1)d
⇒ 0 = 8 + (n - 1) x ( -2 )
⇒ 2 x (n - 1) = 8
⇒ n - 1 = 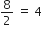
⇒ n = 4 + 1 = 5
अत: दी गई A.P. का 5वाँ पद शून्य है।
किसी A.P. का 17वाँ पद उसके 10वें पद से 7 अधिक है। इसका सार्व अंतर ज्ञात कीजिए।
a17 = a + 16d
a10 = a + 9d
प्रश्नानुसार,
a17 – a10 = 7
⇒ (a + 16d) – (a + 9d) = 7
⇒ a + 16d – a – 9d = 7
⇒ 7d = 7
⇒ d = 1
अत: सार्व अंतर d = 1 है।
A.P. : 3, 15, 27, 39, ... का कौन-सा पद उसके 54वें पद से साधिक होगा?
A.P. : 3, 15,27,39 ...
यहाँ, a1 = 3, a2 = 15
a3 = 27, a4 = 39
d = a2 – a1 = 15 – 3 = 12
a54 = a (54 – 1)d
= 3 + 53 x 12
= 3 + 636 = 639
माना इसका nवाँ पद 54वें पद से 132 अधिक है,
an = a + (n - 1)d
a54 + 132 = a + (n - 1)d![]() 639 + 132 = 3 + (n - 1) x 12
639 + 132 = 3 + (n - 1) x 12![]() 771 - 3 = 12(n - 1)
771 - 3 = 12(n - 1)![]() 768 = 12(n - 1)
768 = 12(n - 1)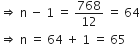
दो समांतर श्रेढियों का सार्व अंतर समान है। इनके 100वें पदों का अंतर 100 है, तो उनके 1000वें पदों का अंतर क्या होगा?
माना सार्व अंतर = d
पहली श्रेढ़ी का प्रथम पद = a
दूसरी श्रेढ़ी का प्रथम पद = b
तब, पहली श्रेढ़ी का 100वाँ पद = a + 99d
दूसरी श्रेढ़ी का 100वाँ पद = b + 99d
उनके वें पदों में अंतर = 100 [ दिया है ]
⇒ (a + 99d) – (b + 99d) = 100
⇒ a – b = 100 ...(i)
पहली श्रेढ़ी का a1000 = a + 999d
दूसरी श्रेढ़ी का a1000 = b + 999d
अत: उनके 1000वें पदों का अंतर = (a + 999d) (b + 999d) = a – b
= 100 [ (i) द्वारा ]
तीन अंकों वाली कितनी संख्याएँ 7 से विभाज्य हैं?
105, 112, 119, ..., 994
यहाँ, a = 105
d = 112 - 105 = 7
an = 994
an = a + (n -1)d

अत: 128, 3 अंकीय संख्याएँ 7 से विभाज्य है।
10 और 250 के बीच में 4 के कितने गुणज हैं?
10 और 250 के बीच 4 के गुणज हैं: 12, 16, 20, ..., 248
यहाँ, a = 12
d = 16 - 12 = 4
an = 248
an = a + (n - 1)d
⇒ 248 = 12 + (n - 1) x 4
⇒ 248 - 12 = (n - 1) x 4
⇒ 236 = (n - 1) x 4
⇒ n - 1 = 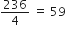
⇒ n = 59 + 1 = 60
अत: 4 के 60 गुणज 10 और 250 के बीच स्थित हैं।
n के किस मान के लिए, दोनों समांतर श्रेढियों 63, 65, 67, ... और 3, 10, 17, ... के nवें पद बराबर होंगे?
दी गई A.P. 63, 65, 67, ... और 3, 10, 17, ... हैं
यहाँ, a1 = 63, a2 = 65, a3 = 67
और b1 = 3, b2 = 10, b3 = 17
माना d1 और d2 क्रमश: दोनों A.P. के सार्व अंतर हैं
तब,
d1 = 65 – 63 = 67 – 65 = 2
d2 = 10 – 3 = 17 – 10 = 7
अब, पहली A.P. का nवाँ पद = a1 + (n – 1)d1
दूसरी A.P. का nवाँ पद = b1 + (n – 1 )d2
∵ दोनों A.P. के nवें पद समान हैं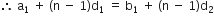
![]() 63 + (n - 1) x 2 = 3 + (n - 1) x 7
63 + (n - 1) x 2 = 3 + (n - 1) x 7![]() 63 + 2n -2 = 3 + 7n - 7
63 + 2n -2 = 3 + 7n - 7![]() 2n + 61 = 7n - 4
2n + 61 = 7n - 4![]() 7n - 2n = 61 + 4
7n - 2n = 61 + 4![]() 5n = 65
5n = 65![]()
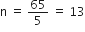
अत: n का अभीष्ट मान = 13
A.P. : 3, 8, 13, ..., 253 में अंतिम पद से 20वाँ पद ज्ञात कीजिए।
3, 8, 13, ..., 253
यहाँ, a = 3
d = 5
l = 253
n = 20
l – (n – 1)d द्वारा आखरी पद से वाँ पद होगा
= 253 – (20 – 1)5
= 253 – (19 x 5)
= 253 – 95 = 158
किसी A.P. के चौथे और 8वें पदों का योग 24 है तथा छठे और 10वें पदों का योग 44 है। इस A.P. के प्रथम तीन पद ज्ञात कीजिए।
a4 + a8 = 24
⇒ a + (4 – 1)d + a + (8 – 1)d = 24
⇒ a + 3d + a + 7d = 24
⇒ 2a + 10d = 24
⇒ a + 5d = 12 ...(i)
a6 + a10 = 44
⇒ a + (6 – 1)d + a + (10 – 1)d = 44
⇒ a + 5d + a + 9d = 44
2a + 14d = 44
⇒ a + 7d = 22 ...(ii)
समीकरण (ii) में से समीकरण (i) को घटाने पर
(a + 7d) – (a + 5d) = 22 – 12
⇒ a + 7d – a – 5d = 10
⇒ 2d = 10
⇒ d = 5
d का मान समीकरण (i) में रखने पर
a1 + 5 x 5 = 12
a1 = 12 - 25 = - 13
a2 = - 13 + 5 = - 8
a3 = - 8 + 5 = - 3
सुब्बा राव ने 1995 में 5000 रु के मासिक वेतन पद पर कार्य आरम्भ किया और प्रत्येक वर्ष 200 रु की वेतन वृद्धि प्राप्त की। किस वर्ष उसका वेतन 7000 रु हो गया?
5000, 5200, 5400, 5600, ...
यहाँ, a = 5000, d = 200, an = 7000
an = a + (n – 1) d
⇒ 7000 = 5000 + (n – 1) 200
⇒ 7000 = 5000 + 200n – 200
⇒ 7000 = 4800 + 200n
⇒ 200n = 2200
⇒ n = 11
11 वर्ष बाद अर्थात 2006 में उसकी आय 7000 रु हो जाएगी।
रामकली ने किसी वर्ष के प्रथम सप्ताह में 5 रु की बचत की और फिर अपनी साप्ताहिक बचत 1.75 रु बढ़ाती गई। यदि nवें सप्ताह में, उसकी साप्ताहिक बचत 20.75 रु हो जाती है, तो n ज्ञात कीजिए।
5, 6.75, 8.50, 10.25, ..., 20.75
यहाँ, a = 5, d = 1.75, an = 20.75
an = a + (n - 1) d![]() 20.75 = 5 + (n - 1) (1.75)
20.75 = 5 + (n - 1) (1.75)![]() 20.72 = 5 + 1.75 n - 1.75
20.72 = 5 + 1.75 n - 1.75![]() 20.75 = 1.75 n + 3.25
20.75 = 1.75 n + 3.25![]() 1.75n = 17.5
1.75n = 17.5![]()
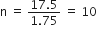
n = 10
अत: 10वें सप्ताह में उसकी बचत 20.75 रु होगी।
निम्नलिखित समांतर श्रेढियों का योग ज्ञात कीजिए:
2, 7, 12, ... 10 पदों तक
यहाँ, a = 2
d = 7 – 2 = 12 – 7 = 5
n = 10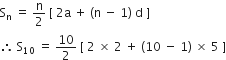
= 5 x [4 + 9 x 5]
= 5 x [4 + 45]
= 5 x 49 = 245
अत: दी गई A.P. के प्रथम पदों का योगफल = 245
निम्नलिखित समांतर श्रेढियों का योग ज्ञात कीजिए:
– 37, – 33, – 29, ... 12 पदों तक
यहाँ, a = – 31
d = – 33 – (– 37)
= – 33 + 37 = 4
n = 12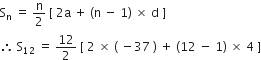
= 6 [ - 74 + 11 x 4 ]
= 6 x [ - 74 + 44 ]
= 6 x ( - 30 ) = - 180
अत: दी गई A.P. के प्रथम 12 पदों का योगफल = – 180
निम्नलिखित समांतर श्रेढियों का योग ज्ञात कीजिए:
0.6, 1.7, 2.8, ... 100 पदों तक
यहाँ, a = 0.6
d = 1.7 – 0.6 = 1.1, n = 100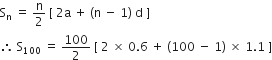
= 50 x [ 2 x 0.6 + (100 - 1) x 1.1 ]
= 50 x [ 1.2 + 108.9 ]
= 50 x 110.1 = 5505.0
अत: दी गई A.P. के प्रथम 100 पदों का योगफल = 5505
निम्नलिखित समांतर श्रेढियों का योग ज्ञात कीजिए: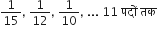
यहाँ, 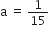
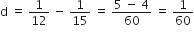
n =11
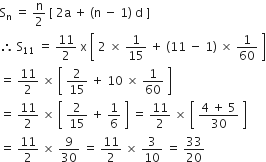
अत: दी गई A.P. के प्रथम 11 पदों का योगफल = 
नीचे दिए हुए योगफलों को ज्ञात कीजिए:
34 + 32 + 30 + . . . + 10
a = 34, d = – 2, an = 10 = l
an = a + (n – 1)
⇒ 10 = 34 + (n – 1) (–2)
⇒ 10 = 34 –2n + 2
⇒ 10 = 36 – 2n
⇒ –26 = –2n ⇒ n = 13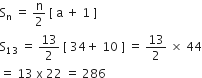
नीचे दिए हुए योगफलों को ज्ञात कीजिए:
–5 + (–8) + (–11) + . . . + (–230)
a = - 5, d = - 3, an = - 230 = l
an = a + (n - 1)d
⇒ - 230 = - 5 + (n - 1) ( -3 )
⇒ - 230 = - 5 - 3n + 3
⇒ - 230 = - 2 - 3n
⇒ - 228 = - 3n
⇒ n = 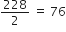
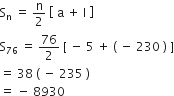
एक A.P. में,
a = 5, d = 3 और an = 50 दिया है। n और Sn ज्ञात कीजिए।
यहाँ, a = 5, d = 3, an = 50
an = a + (n – 1 )d
⇒ 50 = 5 + (n – 1) x 3
⇒ 50 – 5 = 3 x (n – 1)
⇒ 45 = 3 x (n – 1)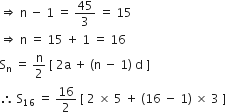
= 8 x [ 10 + 15 x 3]
= 8 x 10 + 45
= 8 x 55 = 440
n = 16
Sn = S16 = 440
एक A.P. में,
a = 7 और a13 = 35 दिया है। d और S13 ज्ञात कीजिए।
यहाँ, a = 7, a13 =35
an = a + (n - 1)d![]() a13 = 7 + (13 - 1)d
a13 = 7 + (13 - 1)d![]() 35 = 7 + 12d
35 = 7 + 12d![]() 35 - 7 = 12d
35 - 7 = 12d![]() 12d = 28
12d = 28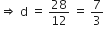
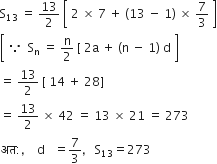
एक A.P. में,
a12 = 37 और d = 3 दिया है। a और S12 ज्ञात कीजिए।
यहाँ, a12 = 37, d= 3
an = a + (n - 1)d![]() a12 = a + (12 - 1) x 3
a12 = a + (12 - 1) x 3![]() 37 = a + 11 x 3
37 = a + 11 x 3![]() a = 37 - 33 = 4
a = 37 - 33 = 4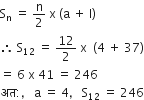
एक A.P. में,
a3 = 15 और S10 = 125 दिया है। d और a10 ज्ञात कीजिए।
यहाँ, a3 = 15
S10 = 125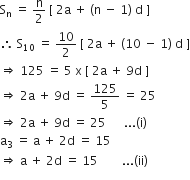
समीकरण (i) और (ii) को हल करने पर
5d = - 5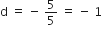
d का मान समीकरण (ii) में रखने पर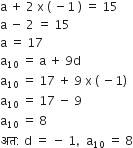
एक A.P. में,
a = 2, d = 8 और Sn = 90 दिया है। n और an ज्ञात कीजिए।
यहाँ, a = 2, d = 8, Sn = 90
Sn =  [ 2 x 2 + (n - 1) d ]
[ 2 x 2 + (n - 1) d ]![]() 180 = n [ 2 x 2 (n - 1) x 8 ]
180 = n [ 2 x 2 (n - 1) x 8 ]![]() 180 = n ( 8n - 4 )
180 = n ( 8n - 4 )![]() 180 = 8n2 - 4n
180 = 8n2 - 4n![]() 8n2 - 4n - 180 = 0
8n2 - 4n - 180 = 0![]() 2n2 - n - 45 = 0
2n2 - n - 45 = 0![]() 2n ( n - 5 ) ( 2n + 9 ) = 0
2n ( n - 5 ) ( 2n + 9 ) = 0![]() n - 5 = 0, 2n + 9 = 0
n - 5 = 0, 2n + 9 = 0![]() n = 5, n =
n = 5, n = 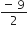
परन्तु पदों की संख्या ऋणात्मक नहीं हो सकती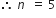
a5 = a+ 4d
= 2 + 4 + 8
अत:, n = 5, an = 34
एक A.P. में,
a = 8, an = 62 और Sn = 90 दिया है। n और d ज्ञात कीजिए।
यहाँ, a = 8
an = 62
Sn = 210
an = a + (n - 1)d![]() 62 - 8 = (n - 1)d
62 - 8 = (n - 1)d![]() 54 = (n -d)d ...(i)
54 = (n -d)d ...(i)
Sn = 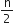 [ 2a - (n - 1) d ]
[ 2a - (n - 1) d ]![]() 210 =
210 = 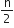 [ 2 x 8 + (n - 1) d ]
[ 2 x 8 + (n - 1) d ]![]() 420 = n [ 16 +(n - 1) d ] ...(ii)
420 = n [ 16 +(n - 1) d ] ...(ii)
समीकरण (i) और (ii) से
420 = n [ 16 + 54 ]![]() 420 = 70n
420 = 70n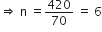
n का मान समीकरण (i) में रखने पर
54 = (6 - 1) x d![]() 5d = 54
5d = 54![]() d =
d = 
अत:, n = 6, d = 
एक A.P. में,
an = 4, d = 2 और Sn = - 14 दिया है। n और a ज्ञात कीजिए।
यहाँ, an = 4, d = 2
Sn = – 14
an = a + (n - 1)d
⇒ 4 = a + (n - 1) x 2
⇒ 4 = a + 2n - 2
⇒ a + 2n = 6 ![]() a = 6 - 2 n ... (i)
a = 6 - 2 n ... (i)
Sn = 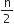 [ 2a + ( n - 1 ) d ]
[ 2a + ( n - 1 ) d ]
⇒ - 14 = 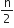 [ 2a + ( n - 1 ) x 2 ]
[ 2a + ( n - 1 ) x 2 ]
⇒ - 28 = n [ 2a + 2 ( n - 1 ) ]
⇒ - 28 = 2n [ a + ( n - 1 ) ]
⇒ - 14 = n [ a + ( n - 1 ) ] ... (ii)
a का नाम समीकरण (ii) में रखने पर
– 14 = n [ 6 – 2n + n – 1 ]
⇒ – 14 = n [ 5 – n ]
⇒ – 14 = 5n – n2
⇒ n2 – 5n – 14 = 0
⇒ (n – 7) (n + 2) = 0
⇒ n – 7 = 0, n + 2 = 0
⇒ n = 7, n = – 2
परन्तु n ऋणात्मक नहीं हो सकता। ∴ n = 7
n का समीकरण (i) में रखने पर
a + 2 x 7 = 6
⇒ a = 6 – 14 = – 8
यहाँ, n = 7, a = – 8
एक A.P. में,
a = 3, n = 8 और S = 192 दिया है। d ज्ञात कीजिए।
यहाँ, a = 3, n = 8
S = 192 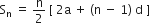
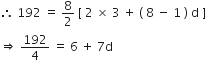
![]() 6 +7d = 48
6 +7d = 48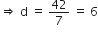
अत:, d = 6
एक A.P. में,
l = 28, S = 144 और कुल 9 पद हैं। a ज्ञात कीजिए।
यहाँ, l = 28, S = 144
n = 9
l = a + (n – 1)d
28 = a + (9 – 1)d
⇒ 28 = a + 8d ...(i)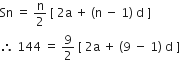
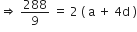
![]() 32 = 2( a + 4d )
32 = 2( a + 4d )![]() a + 4d = 16 ... (ii)
a + 4d = 16 ... (ii)
समीकरण (i) और (ii) को हल करने पर,
a = 32 - 28 = 4
अत:, a = 4
636 योग प्राप्त करने के लिए, A.P. : 9, 17, 25, ... के कितने पद लेने चाहिए?
a = 9
d = 17 - 9 = 8
Sn = 636
Sn = 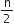 [ 2a + (n - 1) d ]
[ 2a + (n - 1) d ]
⇒ 636 = 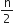 [ 2 x 9 + (n - 1) x 8 ]
[ 2 x 9 + (n - 1) x 8 ]
= 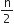 [ 18 + 8 (n - 1) ]
[ 18 + 8 (n - 1) ]
= n [ 5 + 4n - 4 ]
= n [ 5 + 4n ] = 5n + 4n2
⇒ 4n2 + 5n - 636 = 0
द्विघात सूत्र का प्रयोग करने पर,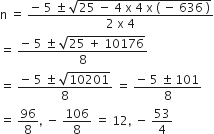
परन्तु पदों की संख्या ऋणात्मक नहीं हो सकती
n = 12
अत: पदों की संख्या 12 है।
किसी A.P. का प्रथम पद 5, अंतिम पद 45 और यौग 400 है। पदों की संख्या और सार्व अंतर ज्ञात कीजिए।
यहाँ, a = 5, l = 45, S = 400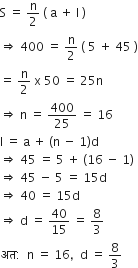
किसी A.P. के प्रथम और अंतिम पद क्रमश: 17 और 350 हैं। यदि सार्व अंतर 9 है, तो इसमें कितने पद हैं और उनका योग क्या है?
यहाँ, a = 17, l = 350, d = 9
l = a + (n - 1)d![]() 350 = 17 + (n - 1) x 9
350 = 17 + (n - 1) x 9![]() 350 - 17 = 9 x (n - 1)
350 - 17 = 9 x (n - 1)![]() 333 = 9 x (n - 1)
333 = 9 x (n - 1)![]() n - 1 =
n - 1 = 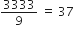
⇒ n = 37 + 1 = 38
अत:, A.P. में 28 पद हैं।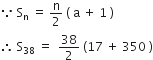
= 19 x 367 = 6973
उस A.P. के प्रथम 51 पदों का योग ज्ञात कीजिए, जिसके दूसरे और तीसरे पद क्रमश: 14 और 18 हैं।
यहाँ, n = 51, a2 = 14, a3 = 18
d = a3 – a2 = 18 – 14 = 4, a2 = a + d
⇒ 14 = a + 4
⇒ a = 14 – 4 = 10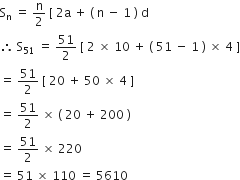
यदि किसी के प्रथम 7 पदों का योग 49 है और प्रथम 17 पदों का योग 289 है, तो इसके प्रथम n पदों का योग ज्ञात कीजिए।
यहाँ, S7 = 49
S17 = 289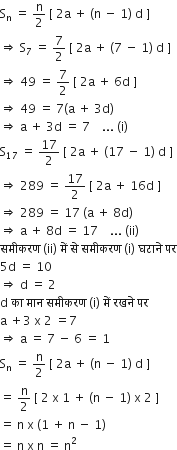
दर्शाइए कि a1, a2, ..., an, ... से एक A.P. बनती है, यदि an नीचे दिए अनुसार परिभाषित है:
an = 3 + 4n
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
an = 3 + 4n ... (i)
a1 = 3 + 4(1) = 3 + 4 = 7
a2 = 3 + 4 (2) = 3 + 8 = 11
a3 = 3 + 4(3) = 3 + 12 = 15
7, 11, 15, ...
यहाँ, a = 7, d = 4, n = 15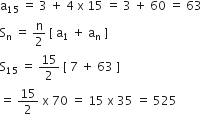
अत: दी गई के प्रथम 15 पदों का योगफल = 525
दर्शाइए कि a1, a2, ..., an, ... से एक A.P. बनती है, यदि an नीचे दिए अनुसार परिभाषित है:
an = 9 - 5n
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
an = 9 – 5n
a1 = 9 – 5(1) = 9 – 5 = 4
a2 = 9 – 5 (2) = 9 – 10 = –1
and a3 = 9 – 5(3) = 9 – 15 = –6
4, –1,–6, –11, ...
यहाँ, a = 4, d = – 5, n = 15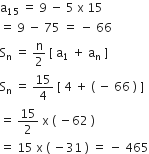
यदि किसी A.P. के प्रथम n पदों का योग 4n - n2 है, तो इसका प्रथम पद ( अर्थात S1 ) क्या है? प्रथम दो पदों का योग क्या है? दूसरा पद क्या है? इसी प्रकार तीसरे, 10वें और nवें पद ज्ञात कीजिए।
पहले n पदों का योग = 4n – n2
⇒ Sn = 4n – n2
जब, n = 1,
S1 = 4(1) – (1)2 = 4 – 1 = 3
⇒ d1 = 3
पहला पद =
n = 2
S2 = 4(2) – (2)2
= 8 – 4 = 4
दूसरा पद = S2 – S1 = 4 – 3 = 1
n = 3
S3 = 4(3) – (3)2
= 12 – 9 = 3
तीसरा पद = S3 – S2 = 3 – 4 = – 1
n = 9, 10
S9= 4(9) – (9)2
= 36 – 81 = – 45
S10 = 4(10) – (10)2
= 40 – 100 = – 60
∴ 10वाँ पद = S10 – S9
= – 60 – (– 45)
= – 60 + 45 = – 15
Sn – 1 = 4(n – 1) – (n – 1)2
= (4n – 4) – (n2 + 1 – 2n)
= 4n – 4 – n2 – 1 + 2n
= 6n – n2 – 5
∴ nवाँ पद = Sn – Sn – 1
= (4n – n2) – (6n – n2 – 5)
= 4n – n2 – 6n + n2 + 5
= 5 –2n
ऐसे प्रथम 40 धन पूर्णांकों का योग ज्ञात कीजिए जो 6 से विभाज्य हैं।
6 से विभाज्य धन पूर्णांक 6. 12, 18, 24, ... जो कि एक A.P. बनाते हैं।
यहाँ, a = 6, d = 6, n = 40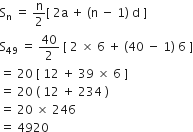
Sponsor Area
8 के प्रथम 15 गुणजों का योग ज्ञात कीजिए।
8 के गुणज हैं: 8, 16, 24, 32, ... जो की एक A.P. बनाते है।
यहाँ, a = 8, d = 16 – 8 = 8, n = 15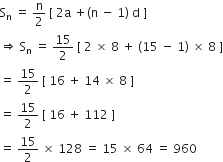
8 के प्रथम 15 गुणजों का योग = 960
0 और 50 के बीच की विषम संख्याओं का योग ज्ञात कीजिए।
0 और 50 के बीच की विषम संख्याएँ
1, 3, 5, 7, ... जो की एक A.P. बनाते हैं।
यहाँ, a = 1, d = 3 – 1 = 2, an = 49
an = a + (n - 1)d
⇒ 49 = 1 + (n - 1) x 2
⇒ 49 - 1 = 2 x (n - 1)
⇒ 48 = 2 x (n - 1 )
⇒ n - 1 = 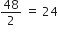
⇒ n = 24 + 1 = 25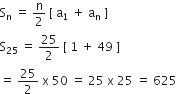
निर्माण कार्य से संबंधित किसी ठेके में, एक निश्चित तिथि के बाद कार्य को विलंब से पूरा करने के लिए, जुर्माना लगाने का प्रावधान इस प्रकार है: पहले दिन के लिए 200 रु, दूसरे दिन के लिए 250 रु, तीसरे दिन के लिए 300 रु इत्यादि, अर्थात प्रत्येक उत्तरोत्तर दिन का जुर्माना अपने से ठीक दिन के जुर्माने से 50 रु अधिक है। एक ठेकेदार को जुर्माने के रूप में कितनी राशि अदा करनी पड़ेगी, यदि वह इस कार्य में 30 दिन का विलंब कर देता है?
यहाँ, a1 = 200, a2 = 250
a3 = 300, d = 50, n = 30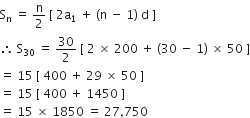
किसी स्कूल के विद्यार्थियों को उनके समग्र शैक्षिक प्रदर्शन के लिए 7 नकद पुरस्कार देने के लिए 700 रु की राशि राखी गई है। यदि प्रत्येक पुरस्कार अपने से ठीक पहले पुरस्कार से 20 रु कम है, तो प्रत्येक पुरस्कार का मान ज्ञात कीजिए।
सार्व अंतर = (a – 20) – a = – 20, n = 7, Sn = 700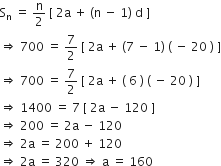
पहला इनाम = 160 रु
दूसरा इनाम = 160 - 20 = 140 रु
तीसरा इनाम = 140 - 20 = 120 रु
चौथा इनाम = 120 - 20 = 100 रु
पाँचवाँ इनाम = 100 - 20 = 80 रु
छठा इनाम = 80 - 20 = 60 रु
सातवाँ इनाम = 60 - 20 = 40 रु
एक स्कुल के विद्यार्थियों ने वायु प्रदूषण कम करने के लिए स्कूल के अंदर और बाहर पेड़ लगने के बारे में सोचा। यह निर्णय लिया गया कि प्रत्येक कक्षा का प्रत्येक अनुभाग अपनी कक्षा की संख्या के बराबर पेड़ लगाएगा। उदारणार्थ, कक्षा I का एक अनुभाग 1 पेड़ लगाएगा, कक्षा II का एक अनुभाग 2 पेड़ लगाएगा, कक्षा III का एक अनुभाग 3 पेड़ लगाएगा, इत्यादि और ऐसा कक्षा XII के लिए चलता रहेगा। प्रत्येक कक्षा के तीन अनुभाग हैं। इस स्कूल के विद्यार्थियों द्वारा लगाए गए कुल पेड़ों की संख्या कितनी होगी?
पहली कक्षा के तीन सैक्शन वृक्ष लगाएंगें = 1 x 3 = 3
दूसरी कक्षा के तीन सैक्शन वृक्ष लगाएंगें = 2 x 3 = 6
तीसरी कक्षा के तीन सैक्शन वृक्ष लगाएंगें = 3 x 3 = 9 ...
12वीं कक्षा के तीन सैक्शन वृक्ष लगाएंगें = 12 x 3 = 36
A .P. : 3, 6, 9, ..., 36
यहाँ, a = 3
d = 6 - 3 = 3
an = 36
an = a +(n -1) d![]() 36 = 3 + (n - 1)d
36 = 3 + (n - 1)d![]() 36 = 3 + (n - 1) x 3
36 = 3 + (n - 1) x 3![]() 36 - 3 = 3 x (n - 1)
36 - 3 = 3 x (n - 1)![]() 33 = 3 x (n - 1)
33 = 3 x (n - 1)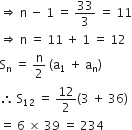
अत: विद्यार्थियों द्वारा लगाए गए कुल वृक्ष = 234
केंद्र A से प्रारंभ हुए, बारी-बारी से केंद्रों A और B को लेते हुए, त्रिज्याओं 0.5 cm, 1.0 cm, 1.5 cm, 2.0 cm, ... वाले उत्तराखर अर्द्धवृत्तों को खींचकर एक सर्पिल बनाया गया है, जैसाकि आकृति में दर्शाया गया है। तेरह क्रमागत अर्द्धवृत्तों से बने इस सर्पिल की कुल लंबाई क्या है? (  लीजिए )
लीजिए )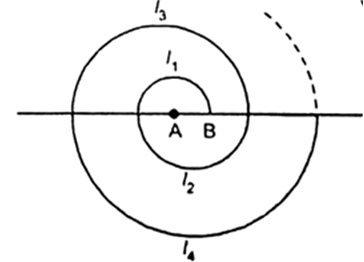
[ संकेत: क्रमश: केंद्रों A, B, A, B, ... वाले अर्द्धवृत्तों की लंबाइयाँ l1, l2, l3, l4 हैं। ]
हम जानते हैं कि
अर्द्धवृत की लंबाई = πr
l1 = π x 0.5 cm
l2 = π x 1.0 cm
l3 = π x 1.5 cm
l4 = π x 2.0 cm इसी तरह
मान चक्राकार स्पिरिंग की कुल लंबाई l है जो कि तेरह अर्द्धवृत्तों से बना है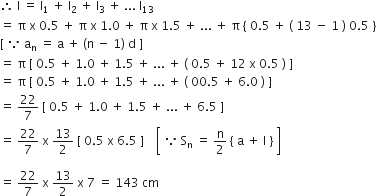
अत: वृत्ताकार स्पिरिंग की कुल लंबाई जो कि तेरह अर्द्धवृत्तों से बना है = 143 cm
200 लठ्ठों को ढेरी के रूप में इस प्रकार रखा जाता है: सबसे नीचे वाली पंक्ति में 20 लठ्ठे, उससे अगली पंक्ति में 19 लठ्ठे उससे अगली पंक्ति में 18 लठ्ठे, इत्यादि ( आकृति में दर्शाए अनुसार )। ये 200 लठ्ठे कितनी पंक्तियों में रखे गए हैं तथा सबसे ऊपरी पंक्ति में कितने लठ्ठे हैं?

सबसे नीचे की पंक्ति में = 20 लठ्ठे
अगली पनकी में = 19 लठ्ठे
उससे अगली पंक्ति में = 18 लठ्ठे
और इसी प्रकार आगे,
अत: 20, 19, 18, ... एक A.P. बनाते हैं।
यहाँ पर a1 = 20, d = 19 – 20 = (– 1)
Sn = 200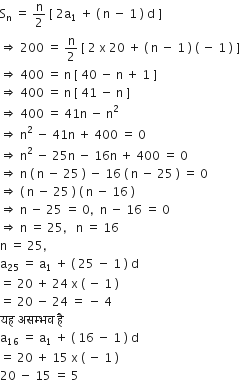
अत: अभीष्ट पंक्तियों की संख्या 16 हैं और सबसे ऊपर वाली पंक्ति में 5 लठ्ठे हैं।
एक आलू दौड़ ( Potato Race ) में, प्रारंभिक स्थ पर एक बाल्टी रखी गई है, जो पहले आलू से 5 m की दूरी पर है तथा अन्य आलुओं को एक सीधी रेखा में परस्पर 3 m की दूरियों पर रखा गया है। इस रेखा पर 10 आलू रखे गए हैं ( आकृति में देखिए )
प्रत्येक प्रतियोगी बाल्टी से चलना प्रारंभ करती है, निकटतम आलू को उठाती है, उसे लेकर वापस आकर दौड़कर बाल्टी में डालती है, दूसरा आलू उठाने के लिए वापस दौड़ती है, उसे उठाकर वापस बाल्टी में डालती है, और वह ऐसा तब तक करती है, जब तक सभी आलू बाल्टी में न आ जाएँ। इसमें प्रतियोगी को कुल कितनी दूरी दौड़नी पड़ेगी?
[ संकेत: पहले और दसूरे आलुओं को उठाकर बाल्टी में डालने तक दौड़ी गई दूरी = 2 x 5 + 2 x ( 5 + 3 ) है। ]
पहले आलू को उठाने और टोकरी में डालने में तय की गई दूरी = 2 x 5 m
दूसरे आलू को उठाने और टोकरी में डालने में तय की गई दूरी = 2 x (5 + 3) m
तीसरे आलू को उठाने और टोकरी में डालने में तय की गई दूरी = 2 x (5 + 6) m
खिलाडी द्वारा दौड़ क्र तय की गई दूरी = 2 x 5 + 2 x (5 + 3) + 2 x (5 + 6) + ... 10 पदों तक
= 10 + 16 + 22 + .... जो कि एक A.P. है
यहाँ, a = 10, d = 16 – 10 = 6, n = 10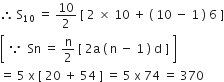
अत: खिलाडी द्वारा दौड़ कर कुल तय की गई दूरी = 370 m
Tips: -
[Hint : To pick up the first potato and the second potato, the total distance (in metres) run by a competitor is 2 × 5 + 2 × (5 + 3)]
A.P. : 12, 117, 113, ... का कौन-सा पद सबसे पहला ऋणात्मक पद होगा?
[ संकेत: an < 0 के लिए n ज्ञात कीजिए। ]
A .P. is 121, 117, 113, ... यहाँ, a = 121
d = 117 – 121 = –4
माना nवाँ पद ऋणात्मक पर है अर्थात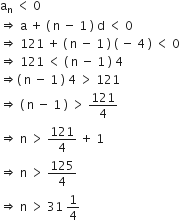
अत: दी गई A.P. का 32वाँ पद पहला ऋणात्मक पद है।
किसी के तीसरे और सातवें पदों का योग 6 है और उसका गुणनफल 8 है। इस के प्रथम 16 पदों का योग ज्ञात कीजिए।
माना एक A.P. का प्रथम पद a1 तथा सार्व अंतर d है, तब,
प्रश्नानुसार,
a3 = a1 + 2d
a7 = a1 + 6d
a3 + a7 = a1 2d + a1 + 6d
= 2a1 8d = 6 ... (i)
a3 x a7 = ( a1 + 2d ) x ( a1 + 6d )
= a12 + 8a1d + 12d2 = 8 ... (ii)
a1 + 4d = 3
a1 = 3 - 4d ... (iii)
a1 का मान (ii) में रखने पर, हम प्राप्त करते हैं
(3 - 4d)2 + 8 (3 - 4d) d + 12d2 = 8
⇒ 9 - 24d + 16d2 + 24d - 32d2 + 12d2 = 8
⇒ -4d2 + 1 = 0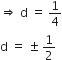
d का मान (iii) में रखने पर, हम प्राप्त करते हैं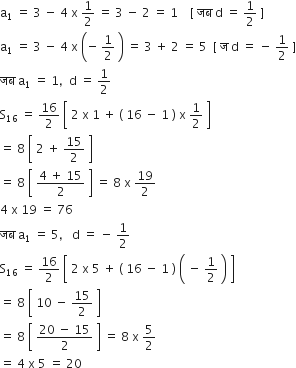
अत: a16 = 20 या 76 है।
एक सीढ़ी के क्रमागत डंडे परस्पर 25 cm दूरी पर है ( आकृति में दर्शाए अनुसार )। डंडों की लंबाई एक समान रूप से घटती जाती है तथा सबसे निचले डंडे की लंबाई 45 cm और सबसे ऊपर वाले डंडे की लंबाई 25 cm है। यदि ऊपरी और निचले डंडे के बीच की दूरी 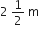 है, तो डंडों को बनाने के लिए लकड़ी की कितनी लंबाई की आवश्यकता होगी?
है, तो डंडों को बनाने के लिए लकड़ी की कितनी लंबाई की आवश्यकता होगी?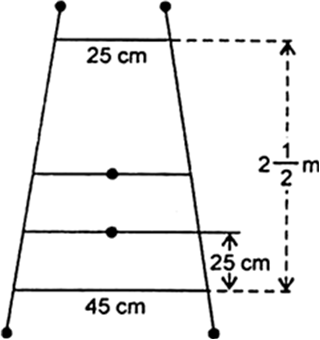
डंडों की संख्या = 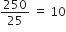
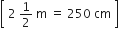
यहाँ, a1 = 45, an = 25, n = 10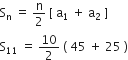
= 5 x 70 = 350 cm
अत: डंडों के लिए अभीष्ट लकड़ी की लंबाई = 350 cm
एक पंक्ति के मकानों को क्रमागत रुप से संख्या 1 से 49 तक अंकित किया गया है। दर्शाइए कि x का एक ऐसा मान है कि x से अंकित मकान से पहले के मकानों कि संख्याओं का योग उसके बाद वाले मकानों की संख्याओं के योग बराबर है। x का मान ज्ञात कीजिए।
[ संकेत: Sx - 1 = S49 - Sx है ]
माना मकानों के नंबर है: 1, 2, 3, ... 49 जो कि एक A.P. में हैं।
यहाँ, a = 1, d = 2 – 1 = 1
प्रश्नानुसार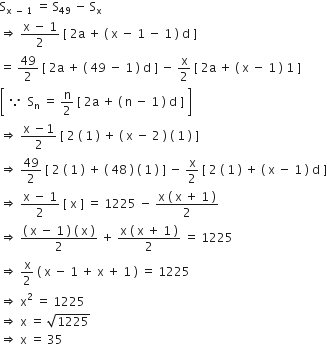
एक फुटबॉल के मैदान में एक छोटा चबूतरा है जिसमें 15 सीढियाँ बानी हुई है। इन सीढ़ियों में से प्रत्येक की लंबाई 50 m है और वह ठोस कंक्रीट की बनी है। प्रत्येक सीढ़ी में 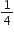 m की चौड़ाई है और
m की चौड़ाई है और 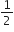 m का फैलाव ( चौड़ाई ) है। ( आकृति में दर्शाए अनुसार )। इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
m का फैलाव ( चौड़ाई ) है। ( आकृति में दर्शाए अनुसार )। इस चबूतरे को बनाने में लगी कंक्रीट का कुल आयतन परिकलित कीजिए।
[ संकेत: पहली सीढ़ी को बनाने में लगी कंक्रीट का आयतन = 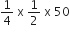 m3 है।
m3 है।
पहली सीढ़ी बनवाने में लगे कंक्रीट का आयतन = 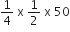 m3
m3
दूसरी सीढ़ी बनवाने में लगे कंक्रीट का आयतन = 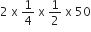 m3
m3
दूसरी सीढ़ी बनवाने में लगे कंक्रीट का आयतन = 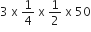 m3
m3
15वीं सीढ़ी बनवाने में लगे कंक्रीट का कुल आयतन = 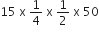 m3
m3
अत: टैरस को बनवाने में लगे कंक्रीट का कुल आयतन =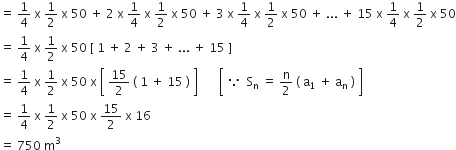
उस A.P. के प्रथम 22 पदों का योग ज्ञात कीजिए, जिसमें d = 7 है और 22वाँ पद 149 है।
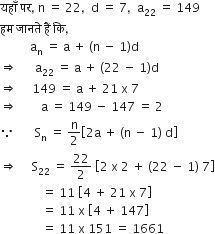
अत: प्रथम 22 पदों का योगफल = 1661
समान्तर श्रेढ़ी 18, 16, 14, ....... के कितने पद लिए जाएँ कि उनका योग शून्य हो?
प्रथम पद, a = 18
सार्व अंतर, d = 16 - 18 = -2
sn = 0 ........ दिया है,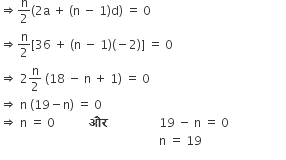
परन्तु n शून्य नहीं हो सकता है।
इसलिये, शब्दों की संख्या, n = 19
यदि एक समान्तर श्रेढ़ी के प्रथम 7 पदों का योग 49 तथा प्रथम 17 पदों का योग 289 है, तो समान्तर श्रेढ़ी के प्रथम n पदों का योग ज्ञात कीजिए।

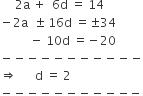
समीकरण (i) में d का मान रखने पर,
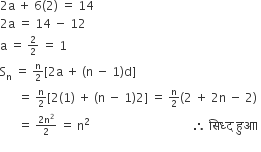
यदि किसी समान्तर श्रेणी का mवां पद  तथा nवां पद
तथा nवां पद 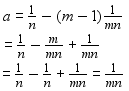 है, तो इसके प्रथम mn पदों का योग ज्ञात कीजिए।
है, तो इसके प्रथम mn पदों का योग ज्ञात कीजिए।
माना a और b दो संख्याएँ हैं जो पहली संख्या AP के समान हैं,
तब,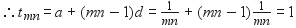
d = 1 mn समीकरण। ..(1) में डालते हैं, जो हमारे पास है,
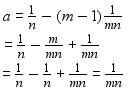
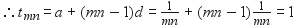
यदि एक समांतर श्रेढ़ी का सार्व-अंतर (d) =-4 तथा सातवाँ पद (a) = 4 है, तो श्रेढ़ी का प्रथम पद ज्ञात कीजिए।
सातवाँ पद a7 = 4
a + 6d = 4
हमें पता है की
an = a + (n-1) d
सार्व-अंतर (d) = -4
a + (-24) = 4
a = 4 + 24 = 28
इसलिए श्रेढ़ी का प्रथम पद 28 है।
3 के पहले 8 गुणज का योग ज्ञात कीजिये
3 के पहले 8 गुणक हैं
3, 6, 9, 12, 15, 18, 21, 24
उपरोक्त अनुक्रम एक A.P. है।
a = 3, d = 3 और l = 24
Mock Test Series
Sponsor Area
Sponsor Area






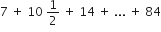
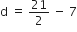


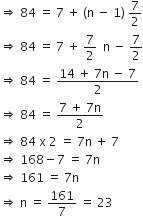
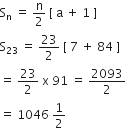
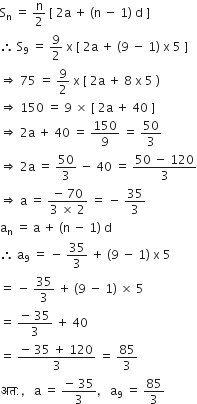
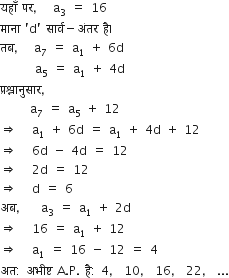
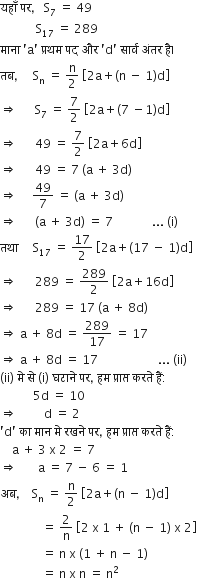
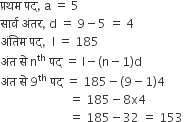



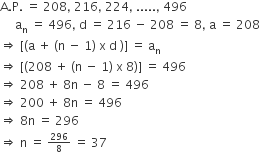
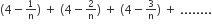 के n पदों का योग ज्ञात करें।
के n पदों का योग ज्ञात करें। 