दर्शाइए कि a1, a2, ..., an, ... से एक A.P. बनती है, यदि an नीचे दिए अनुसार परिभाषित है:
an = 3 + 4n
साथ ही, प्रत्येक स्थिति में, प्रथम 15 पदों का योग ज्ञात कीजिए।
an = 3 + 4n ... (i)
a1 = 3 + 4(1) = 3 + 4 = 7
a2 = 3 + 4 (2) = 3 + 8 = 11
a3 = 3 + 4(3) = 3 + 12 = 15
7, 11, 15, ...
यहाँ, a = 7, d = 4, n = 15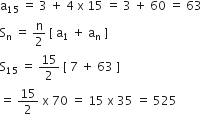
अत: दी गई के प्रथम 15 पदों का योगफल = 525
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = 10, d = 10
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = – 2, d = 0
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = 4, d = – 3
दी हुई A.P. के प्रथम चार पद लिखिए, जबकि प्रथम पद a और सार्व अन्तर d निम्नलिखित है:
a = – 1.25, d = – 0.25
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए:
3, 1, – 1, – 3, ...
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए:
– 5, – 1, 3, 7, ...
निम्नलिखित में से प्रत्येक A.P. के लिए प्रथम पद तथा सार्व अंतर लिखिए:
0.6, 1.7, 2.8, 3.9, ...
Mock Test Series
