Question
एक A.P. में,
an = 4, d = 2 और Sn = - 14 दिया है। n और a ज्ञात कीजिए।
Solution
यहाँ, an = 4, d = 2
Sn = – 14
an = a + (n - 1)d
⇒ 4 = a + (n - 1) x 2
⇒ 4 = a + 2n - 2
⇒ a + 2n = 6 
a = 6 - 2 n ... (i)
Sn =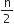 
[ 2a + ( n - 1 ) d ]
⇒ - 14 =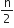 
[ 2a + ( n - 1 ) x 2 ]
⇒ - 28 = n [ 2a + 2 ( n - 1 ) ]
⇒ - 28 = 2n [ a + ( n - 1 ) ]
⇒ - 14 = n [ a + ( n - 1 ) ] ... (ii)
a का नाम समीकरण (ii) में रखने पर
– 14 = n [ 6 – 2n + n – 1 ]
⇒ – 14 = n [ 5 – n ]
⇒ – 14 = 5n – n2
⇒ n2 – 5n – 14 = 0
⇒ (n – 7) (n + 2) = 0
⇒ n – 7 = 0, n + 2 = 0
⇒ n = 7, n = – 2
परन्तु n ऋणात्मक नहीं हो सकता। ∴ n = 7
n का समीकरण (i) में रखने पर
a + 2 x 7 = 6
⇒ a = 6 – 14 = – 8
यहाँ, n = 7, a = – 8
