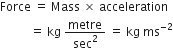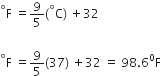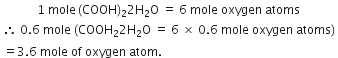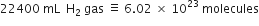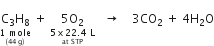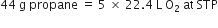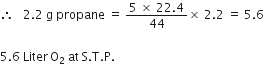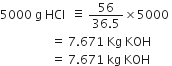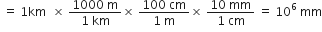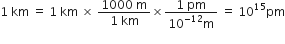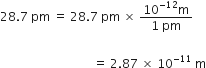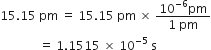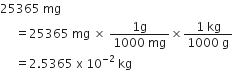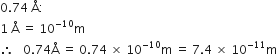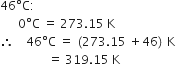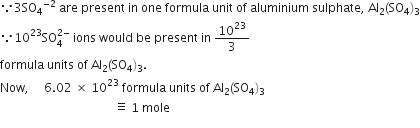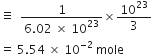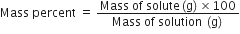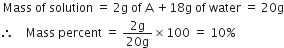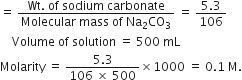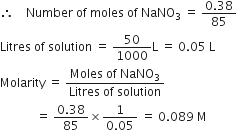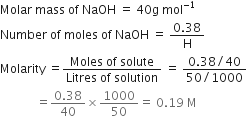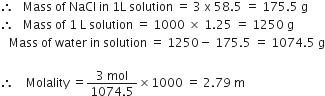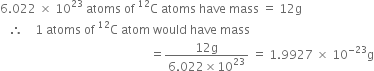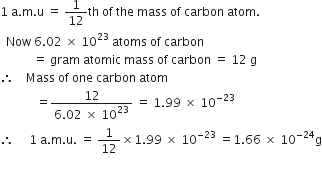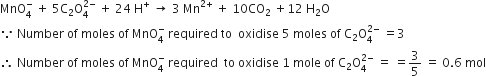Chemistry Part I Chapter 1 Some Basic Concepts Of Chemistry
Sponsor Area
NCERT Solution For Class 11 Physical+education Chemistry Part I
Define the term significant figures.
Significant figures are meaningful digits which are known with certainty.
What is the result of (5.472 - 1.12) to the appropriate number of signficant figures?
The actual difference is 4.352. The reported difference should be only upto two decimal places after rounding
What is the relation between temperature in Kelvin (K) and temperature on centigrade scale?
Temp. on Kelvin (K) = Temp. on centrigrade scale (T°C) + 273.
The popular unit of pressure is atmosphere, how is it related to pascal?
1 atmosphere pressure = 101·324 k Pa
What are SI units of the following:
(i) Density
(ii) Molarity
(iii) Energy
(iv) Temperature ?
(i) kg m-3
(ii) mol m-3
(iii) kg m2 s-2
(iv) Kelvin
Out of 5.00 g and 5.0 g which one is more accurate and why?
Under what conditions air is considered as a heterogenous mixture?
What is gun powder?
It is a mixture of sulfur, charcoal and potassium nitrate(salt peter). The sulgur and charcoal act as fuels, and the saltpeter is an oxidizer.
Sponsor Area
Name the scientist who proposed the law of multiple proportions.
Is there any exception to the law of constant composition?
In case of isotopic compounds, the law does not hold good; for example, 233UF6 and 238UF6·
Why is Gay Lussac's law of combining volumes not obeyed if any rectant or product is not a gas?
If any reactant or product is a liquid, the volume occupied by a liquid is extremely small and hence the law is not obeyed.
Oxides of carbon illustrate which law of chemical combination?
Law of multiple proportions.
Name three elements which make up more than 90 percent of the human body.
Oxygen is about 60 - 70%,
carbon just below 20% and
hydrogen about 10%
These three element make up more than 90 percent of the human body.
If water samples are taken from sea, rivers, clouds, lakes or snow, they will be found to contain hydrogen and oxygen in the appropriate ratio of 1 : 8. This illustrates which law of chemical combination?
What is atomicity of an element?
Why atomic masses are the average values?
What is the relation between molecular weight and vapour density?
Relation between molecular weight and vapour density is,
Molecular weight = 2 x vapour density.
What is the relation between gram molecular weight and volume of a gas?
22.4 litre of a gas at NTP weighs equal or its gram molecular weight.
What is SI unit of mole?
The mole is a base unit of the International System of Units (SI). Unit of mole is mol.
What is G.M.V.?
What is gram atom?
It is the quantity in grams which is numerically equal to the atomic mass of an element on a.m.u. scale.
What is a.m.u.?
One atomic mass unit is defined as a mass exactly equal to one twelfth the mass of one carbon - 12 atom.
1 amu = 1.66056×10–24 g
How many moles of helium gas occupy 22.4 litres at 0°C and 1 atmosphere?
One mole of helium at 0°C and 1 atmosphere occupies 22·4 litres.
The cost of table sugar (C12H22O11) is Rs 6 per kg. What is its cost per mole?
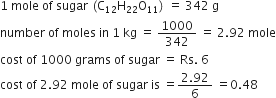
The cost per mole is 0.48 Rs.
Sponsor Area
27 g of Al will react completely with, how many grams of oxygen?
The balanced equation for the given reaction is:
4 Al+ 3 O2 --------> 2Al2O3
Atomic mass of Al = 27g
Atomic mass of O2 = 2 × 16 = 32g
Mole ratio of aluminium and oxygen can be given as:
Al : O2
4 : 3
1 : 3/4
Mass of O2 required = 3/4 × 32 =24g
The vapour density of a gas A is four times that of B. If the molecular mass of B is M what is the molecular mass of A?
According to the relationship:
Mass=2 x Vapour density
we have give mass of B is M, thus Vapour density of B is,
V.D.=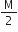
also, given A is four times that of B, then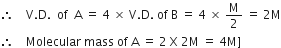
How are empricial and molecular formulae related to each other?
Molecular formula = n (Empricial formula)
where 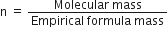
In a certain compound, the percentage of an element (At. mass 12) is 92.3. What is its mole ratio?
We have given,
mass of element =12g
Thus, mole ratio is
92.3/12 =7.69
Two elements A (At. wt. 75) and B (At. wt. 16) combine to give a compound having 75·8%A. Calculate the relative number of atoms present in B.
As, we have given the relative number of A =75.8%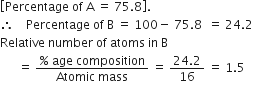
Hence, the relative number of B = 1.5%
A substance has empirical formula CH2O, its vapour density is 30. What is its molecular formula?
Empricial formula mass of CH2O
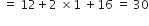
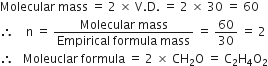
What is stoichiometry?
The word ‘stoichiometry’ is derived from two Greek words - stoicheion (meaning element) and metron (meaning measure). Stoichiometry, thus, deals with the calculation of masses (sometimes volumes also) of the reactants and the products involved in a chemical reaction.
From where the word stoichometry has been derived?
The word ‘stoichiometry’ is derived from two Greek words - stoicheion (meaning element) and metron (meaning measure).
What do you understand by limiting reactant?
When in reaction, one rectant is in excess over the other. The reactant which is present in the lesser amount gets consumed after sometimes and after no further reaction takes place whatever be the amount of the other reactant present. Hence, the reactant which gets consumed, limits the amount of product formed and, therefore, called the liminting reagent.
Define molality (m).

What do you mean by significant figures?
Or
What do you know about significant figures? What are the rules for determing the number of significant figures?
Significant figures. The total number of digits (including the last one, though its value is doubtful) in the number used to express the physical quantity is called the number of significant figures. For example, the reading 24 · 84 cm having three certain digits (2, 4 and 8) and one doubtful digit (4) has four significant figures.
Rules for determining the number of significant figures:
1. Except zero, all the digits 1, 2, 3, 4, 5, 6, 7, 8 and 9 are significant. For example,
4·25 has three significant figures.
71·435 has five significant figures.
2. All digits are significant including zeros if zero appears in between non-zero digits, e.g.,
4·02 has three significant figures.
4·005 has four significant figures.
6·0042 has five significant figures.
3. Zeros to the left of the first non-zero digit in a number are not significant, they merely indicate the positions of the decimal point. e.g.,
0·428 has three significant figures.
0·054 has two significant figures.
0·0006 has one significant figure.
4. Zeros to the right of the decimal point are significant. e.g.,
42·0 has three significant figures.
42·00 has four significant figures.
42·000 has five significant figures.
5. In exponential notation, the numerical portion gives the number of significant figures. e.g.,
1·58 × 10–1 has three significant figures.
4·243 × 105 has four significant figures.
3·24 × 107 has three significant figures.
What do you understand by ‘rounding off’?
The rules for rounding off the non significant figures in the measurements are as under:
1. If the digit following the last digit to be retained is less than 5, the last digit is left unchanged. For example,
4·22 is rounded off to 4·2
4·14 is rounded off to 4·1
4·34 is rounded off to 4·3
2. If the last digit happens to be five (as in 4·335), then a digit before five is checked whether it is odd or even.
If it is odd, then it is increased by one. e.g.
4·335 is rounded off to 4·34
15·275 is rounded off to 15·28
If the digit before five is even, then it is retained as such. e.g.,
14·145 is rounded off to 14·14
6·225 is rounded off to 6·22
0·085 is rounded off to 0·08
3. If the last digit is greater than 5, the last-digit to be retained is increased by one. e.g.,
2·26 is rounded off to 2·3
4·68 is rounded off to 4·7
16·59 is rounded off to 16·6
State the number of significant figures in each of the following numbers:
2·653 × 104
State the number of significant figures in each of the following numbers:
0.00368
State the number of significant figures in each of the following numbers:
653
State the number of significant figures in each of the following numbers:
0.368
0.368 has three significant figures because zeros to the left of the first non-zero digit are not significant.
State the number of significant figures in the following number:
0.0300
How many significant figures are present in the following?
0.0025
How many significant figures are present in the following?
208
How many significant figures are present in the following?
5005
How many significant figures are present in the following?
126,000
How many significant figures are present in the following?
500.0
How many significant figures are present in the following?
2.0034
Express the following numbers to four significant figures:
5.607892
5·608
Express the following numbers to four significant figures:
32.392800
32·39
Express the following numbers to four significant figures:
1·78986 × 103
1·790 × 103
Sponsor Area
Express the following numbers to four significant figures:
0·007837
What are the rules for determining the number of significant figures in answers involving:
(i) addition or subtraction
(ii) multiplication or division
(iii) calculations involving a number of steps?
(i) Addition or subtraction. While carrying out addition or subtraction of a number of terms, the result should be reported to the same number of decimal places as that of the term with the least number of decimal places.
(a) Addition of number. Ex. 3·5 g of NaCl and 4·23 g of KCI were dissolved in 25·001 g of water. What is the properly reported mass of solution?
Sol. +3·5 (this is the term with the least number of decimal place)
+ 4.23
+ 25.001
_______
Actual sum = 32.731 g
The respected sum should be only one decimal place after rounding off.
∴ Correct mass of the solution = 32·7 g
(b) Subtraction of number. Ex. Express the result of the following observations to the appropriate number of significant figures: 12·87 – 0·0107.
Sol. 12·87 (this is the term with the least number of decimal place)
-0.0107
________
Actual difference = 12.8693
The reported difference should be only upto two decimal places after rounding off.
∴ Reported difference = 12·87
(ii) Multiplication or division. While carrying out multiplication or division, the number of significant figures in the final result should not exceed the number of significant figures in the least precise factor.
(a) Multiplication of number
Ex. Complete the result of the following calculation to the appropriate number of significant figures:
87·4 × 0·00457
Sol. 87·4 × 0·00457 = 0·399418
As the number of significant figures in the least precise factor is three, therefore the reported result after rounding off is 0·399.
(b) Division of number.
Ex. Express the result of the following calculation to the appropriate number of significant figures:
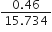
Sol. 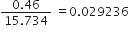
As the number of significant figures in the least precise factor is two (viz 0·46), therefore the reported result after rounding off is 0·029 (containing only two significant figures).
(iii) Calculations involing a number of steps: If a calculation involves a number of steps, the result should contain the same number of significant figures as that of the least precise number involved other than the exact numbers.
Compute the following keeping in view the proper number of significant figures: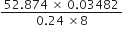
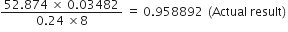
Leaving the exact number 8, the least precise term has two significant figures. Therefore, the reported result after rounding off is 0·96 (containing only two significant figures).
Express the result of the following calculations to the appropriate number of siginficant figures: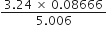
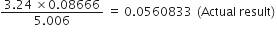
As the number of significant-figures in the least precise factor is three (viz 3.24), therefore, the reported result after rounding off is 0·0561 (containing only three significant figures).
Express the result of the following calculations to the appropriate number of siginficant figures: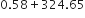
0·58 + 325·65 = 324·23 (Actual result)
While carrying out addition of a number of terms, the result should be reported to the same number of decimal places as that of the term with the least number of decimal places. In the present case, both the given numbers have two decimal places, therefore, the reported sum should be only two decimal places after rounding off.
∴ Correct sum = 325·23
Express the result of the following calculations to the appropriate number of siginficant figures:
943 × 0·00345 + 101
= 3·25335 + 101
= 3·25 + 101 (Applying the rule of product)
= 104·25
= 104 (Applying the rule of addition)
How many significant figures should be present in the answer of the following calculations?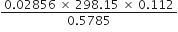
How many significant figures should be present in the answer of the following calculations?
How many significant figures should be present in the answer of the following calculations?![]()
The population of India according to 1981 census figure was 68.4 crores. Express it in scientific notation.
Calculate the area of a rectangle whose length is 6.00 m and breadth 5.2 m. Express the result to a proper number of significant figures.
Area of rectangle = Length × Breadth = 6·00 m × 5·2 m = 31·200 m2
As the number of significant figures in the least precise factor is two, therefore, the correct answer is 31m2.
What do you know about the most scientific system of units?
Seven basic SI Units.
|
Quantity |
Unit |
Symbol |
|
Length |
metre |
m |
|
Mass |
kilogram |
kg |
|
Time |
second |
s |
|
Electric current |
ampere |
A |
|
Thermodynamic,Temperature |
kelvin |
K |
|
Amount of substance |
mole |
mol |
|
Luminous intensity |
Candela |
|
What is the S.I. unit of mass? How is it defined?
Match the following prefixes with their multiples:
| A. micro | (i) 106 |
| B. deca | (ii) 109 |
| C. mega | (iii) 10–6 |
| D. giga | (iv) 10–15 |
| E. femto | (v) 10 |
A. micro | (i) 10–6 |
B. deca | (ii) 10 |
C. mega | (iii) 106 |
D. giga | (iv) 109
|
E. femto | (v) 10–15 |
A train covers a distance of 144 kilometers in two hours. What is the speed of the train in m/s.
Distance covered = 144 kilometers
= 144 x 1000 m
Time taken = 2 hours = 2 x 60 x 60 second
What do you mean by Dimensional Analysis (Derived units)?
From the seven basic or fundamental units, the units of some other physical quantities such as area, volume, pressure, force, speed, velocity etc. can be derived. These are called derived units. Derived unit of a physical quantity is also called dimensional formula of that quantity. For example, the unit of area can be derived as: Area = Length × Breadth If length = 6 m and breadth = 5m, then Area = 6m × 5m = 30m2
Unit for area is m2
Some common derived units are listed below:
Derived Units
|
Physical Quantity |
Units |
Symbol for Unit |
Definition in S.I. Basic Units |
|
Area |
square metre |
m2 |
m2 |
|
Volume |
cubic metre |
m3 |
m3 |
|
Density |
kilogram per cubic |
kg/m3 or kg m–3 |
|
|
Speed |
metre per second |
m/s or ms–1 |
|
|
Acceleration |
metre per second |
||
|
Force |
newton |
N |
kg ms–2 |
|
Pressure |
pascal |
Pa |
kg m–1s–1 or Nm–2 |
|
Energy |
joule |
J |
kg m2 s–2 |
|
Frequency |
hertz |
Hz |
s–1 |
|
Electric charge |
coulomb |
C |
A Sec = amp second |
|
Electric resistance |
ohm |
Ω |
m2 kg s–3 A–2 |
|
Electric potentialdifference |
volt |
V |
kg m2 s–3 A–1 or JA–1 S–1 |
If the speed of light is 3·0 × 108 ms–1, calculate the distance covered by light in 2.00 ns.
Distance covered = Speed x Time
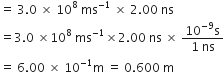
Pressure is determined as force per unit area of the surface. The SI unit of pressure, pascal is as shown below:
1 Pa = 1N m–2
If mass of air at sea level is 1034 g cm–2, calculate the pressure in pascal.
But weight = mg
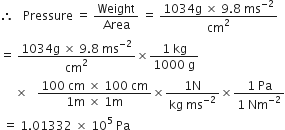
Express each of the following in SI units:
93 million miles (this is the distance between the earth and the sun)
93 million miles:
1 mile = 1.60 kilometre = 1.60 x 103 m
93 million miles = 93 x 106 miles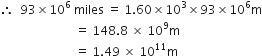
Express each of the following in SI units:
5 feet 2 inches (the average height of an Indian female).
5 feet 2 inches:
5 feet 2 inches = 62 inches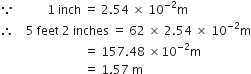
Express each of the following in SI units:
100 miles per hour (the typical speed of Rajdhani Express).
1 mile = 1.60 kilometre = 1.60 x 103 m
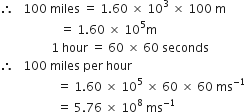
Express each of the following in SI units:
150 pounds (average weight of an Indian male).
150 pounds:
1 pound = 454 x 10-3 kg
150 pounds = 454 x 10-3 x 150 kg = 68.1 kg
Define matter. Briefly describe the physical classification (three different stages) of matter.
Matter. Matter is defined as anything which occupies space and has mass. On the basis of physical state, it has been classified as solids, liquids and gases.
(i) Solids are rigid substances which have definite shape and possess definite volume. For example, table, book, silver, wood etc.
(ii) Liquids are those mobile substances which have no definite shape but possess definite volume. They take up the shape of the vessel in which they are put. For example, milk, water, oil, mercury etc.
(iii) Gases are those mobile substances which have no fixed shape or volume. Gases flow to assume the shape of the container. For example, nitrogen, hydrogen, carbondioxide etc.
Describe briefly the chemical classification of matter.
Or
Define the terms element, compound and mixture.
According to chemical classification, matter can be classified into two types:
(i) Pure substances
(ii) Mixtures
(i) Pure substances: A pure substance is made up of one type of substance. It can be further classified into two types:
(a) Elements
(b) Compounds
(a) Elements. An element is defined as pure substance that contains only one kind of atoms. An element has definite physical and chemical properties. For example, hydrogen, phosphorus, iodine and sulphur are all elements. There are 105 elements known at present.
(b) Compounds. A compound is a pure substance containing two or more than two elements combined together in some definite proportion by weight and which can be decomposed into its constituent elements by chemical means. For example, water is a compound formed by the combination of elements hydrogen and oxygen in a fixed proportion, 1 : 8 by weight. Water can also be decomposed into hydrogen and oxygen by passing electricity through it.
(ii) Mixtures. A mixture is made up of two or more than two substances in varying amounts and can be separated into constituents by some suitable physical means. Mixtures are of two types:
(a) Homogenous mixtures
(b) Heterogenous mixtures.
(a) Homogenous mixtures: Homogenous mixtures are the mixtures which have same composition throughout. For example, air is a homogenous mixture of a number of gases like oxygen, nitrogen, CO2 etc. Similarly alloys are homogenous mixtures of metals.
(b) Heterogenous mixtures: Heterogenous mixtures are the mixtures which have different compositions in different parts. For example, a mixture of sand and sugar and a mixutre of sulphur and sand etc.
Give the points of difference between mixture and compound.
|
Mixture 1. The components of a mixture may be present in any ratio. |
Compound 1. The components of a compound are always present in a fixed ratio by mass. |
|
2. Mixture may be homogeneous or heterogeneous in nature. |
2. Compounds are always homogeneous. |
|
3. The components of a mixture can be easily separated by simple physical or chemical means. |
3. The constituents (elements) of the compound cannot be separated either by physical or mechanical means. They can, however, be separated using heat or light (chemical means). |
|
4. Components of the mixture can be easily seen with naked eye or with magnifying glass. |
4. Components of the compound can in no case be seen with naked eye or with a magnified lense. |
|
5. The properties of a mixture are midway between those of its constituents. |
5. The properties of a compound are entirely different from those of its constituents. |
Define the terms:
(i) Metals (ii) Non-metals (iii) Metalloids.
(i) Metals. Metals are generally solids and possess characteristics such as bright lustre, hardness and ability to conduct electricity and heat. These are generally malleable and ductile. For example, copper, iron, gold, silver etc.
(ii) Non-metals. These elements are generally non-lustrous, brittle and poor conductors of heat and electricity. For example, carbon, hydrogen, oxygen etc.
(iii) Metalloids. Metalloids are elements which show properties common to both metals and non-metals. For example, arsenic, antimony, bismuth etc.
Classify the following as pure substances or mixtures: air, milk, graphite, diamond, gasoline, tap water, distilled water, oxygen, one rupee coin, 22 carat gold, steel, iron, sodium chloride, iodized table salt.
Pure substances: Graphite, Diamond, Distilled water, Oxygen, Iron, Sodium chloride,22 carat gold.
Mixtures : Air, Milk, Gasoline, Tap water, One rupee coin, Steel, Iodised table salt.
Separate the following substances into elements and compounds: Graphite, Diamond, Distilled water, Oxygen, Iron, Sodium chloride, Blue vitriol.
Elements: Graphite, Diamond, Oxygen, Iron.
Compounds: Distilled water, Sodium chloride, Blue vitriol.
How will you separate the following mixtures?
(i) Oil and water
(ii) Iron-filings and saw dust.
(iii) Glass powder and sugar.
(i) Oil and water. As oil and water are usually immiscible with each other and form two separate layers, these layers can be separated with the help of separating funnel.
(ii) Iron-filings and saw dust. This mixutre can be separated by rolling a magnet into the mixture. Iron filings are attracted towards the magnet and stick to it leaving the saw dust behind.
(iii) Glass powder and sugar. The mixture is shaken with water in a beaker. Sugar dissolves in water whereas glass powder does not. The solution is filtered. Glass is left behind as residue while sugar solution is collected as filtrate. From the filtrate, sugar may be obtained by evaporation of water or by crystallisation process.
Define the law of conservation of mass. How will you verify this law?

Verification. This law can be verified with the help of Landolt’s experiment. Landolt took the solutions of sodium chloride and silver nitrate separately in two limbs of Landolt’s tube. The tube was weighed and sealed. After weighing, the two solutions were mixed thoroughly by shaking the tube. As a result, silver nitrate reacted with sodium chloride to from a white precipitate of silver chloride.
After the reaction, the tube was again weighed and weight was found to be the same as it was before the chemical reaction. This confirms the truthfulness of the law.
When 4·2g of NaHCO3 (sodium hydrogen carbonate) is added to a solution of CH3COOH (acetic acid) weighing 10·0g, it is observed that 2·2g of CO2 is released into atmosphere. The residue is found to weigh 12·0g. Show that these observations are in agreement with the law of conservation of mass.
The reaction is 
Total mass of the reactants
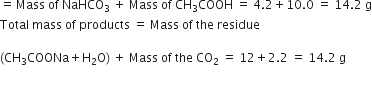
Thus, total mass of reactants (14.2) g
= Total mass of products (14.2) g
This illustrates the law of conservation of mass.
If 6.3g of NaHCO3 are added to 15.0 g of CH3COOH solution, the residue is found to weigh 18.0g. What is the mass of CO2 released in the reaction?
The reaction is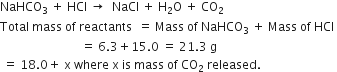
According to the law of conservation of mass:
Total mass of reactants = Total mass of products
21.3 = 18.0 + x
or x = 21.3 - 18.0 = 3.3 g
State the law of constant composition or Definite proportion. Explain with suitable examples.
Law of constant composition (Louis Proust, 1799) states that a pure chemical compound, regardless of its source, is always made up of the same elements, combined together in a fixed proportion by weight.
For example, carbon dioxide can be obtained by a number of methods:
(i) by burning coal or candle
(ii) by respiration
(iii) by heating limestone (CaCO3)
(iv) by the action of dilute hydrochloric acid on marble pieces.
It has been observed that each sample of carbon dioxide contains carbon and oxygen elements in the ratio of 3:8 by weight.
In an experiment 4.68 g iron oxide on reduction with hydrogen yields 3.86 g of iron. In another experiment 3.88 g of iron oxide gives 3.2 g of iron on reduction with hydrogen. Prove that the above data illustrates the law of constant proportions.
Mass of iron oxide = Mass of iron oxide - Mass of iron = (4.68 - 3.86) = 0.82 g
Ratio of oxygen and iron = 0.82 : 3.86 = 1:4.707
In the second experiment:
The mass of iron oxide = 3.88 g
The mass of iron after reduction = 3.20 g
Mass of iron oxide = Mass of iron oxide - Mass of iron = (3.88-3.20) = 0.68g
Ratio of oxygen and iron=0.68:3.20 =1:4.706
Thus, the data illustrates the law of consant proportions as in both the experiments the ratio of oxygen and iron is the same.
Sponsor Area
Weight of copper oxide obtained by treating 2.16 g of metallic copper with nitric acid and subsequent ignition was 2·7g. In another experiment, 1 · 15 g of copper oxide on reduction yielded 0·92g of copper. Show that the result illustrates the law of definite proportion.
Weight of copper = 2.16 g
Weight of copper oxide obtained on ignition = 2.70 g
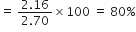

In the second experiment.
Weight of copper oxide = 1.15 g


Thus, the data illustrates the law of definite porportion as in both the experiments the percentage of copper and oxygen are same.
If law of constant composition is true, what weights of calcium, carbon and oxygen are present in 1.5 g fo calcium carbonate? Given that a sample of calcium carbonate from another sample contains the following percentage composition:
Ca = 40.0%; C = 12.0%; O= 48.0%
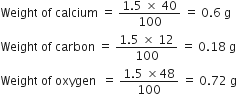
State and explain the law of multiple proportions.
Law of multiple proportions (John Dalton 1804) states that when two elements combine to form two or more compounds, the weight of one of the elements which combines with a fixed weight of the other, bears a simple whole number ratio. For example, hydrogen and oxygen combine to form two compounds H2O (water) and H2O2(hydrogen peroxide). In water, Hydrogen 2 parts and oxygen 16 parts In hydrogen peroxide hydrogen 2 parts and oxygen 32 parts.
The weights of oxygen which combine with same weight of hydrogen in these two compounds bear a simple ratio 1 : 2. Nitrogen forms five stable oxides:
N2O Nitrogen 28 parts Oxygen 16 parts
N2O2 Nitrogen 28 parts Oxygen 32 parts
N2O3 Nitrogen 28 parts Oxygen 48 parts
N2O4 Nitrogen 28 parts Oxygen 64 parts
N2O5 Nitrogen 28 parts Oxygen 80 parts
The weight of oxygen which combines with same weight of nitrogen in the five compounds bear a ratio 16 : 32 : 48 : 64 : 80 : or 1 : 2 : 3 : 4 : 5.
The following data were obtained when dinitrogen and dioxygen react together to form different compounds:
Mass of dinitrogen Mass of dioxygen
(i) 14g 16g
(ii) 14g 32g
(iii) 28g 32g
(iv) 28g 80g
which law of chemical combination is obeyed by the above experimental data? Give its statement?
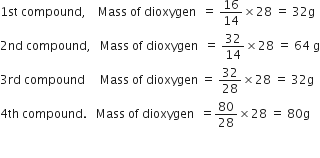 These are in the ratio of 32 : 64 : 32 : 80 i.e. 1:2:1:5 which is simple whole number ratio. Hence the given data obeys the law of multiple proportions. For definition refer to the answer of question 40.
These are in the ratio of 32 : 64 : 32 : 80 i.e. 1:2:1:5 which is simple whole number ratio. Hence the given data obeys the law of multiple proportions. For definition refer to the answer of question 40.Carbon and oxygen are known to form two compounds. The carbon content in one of these is 42·9% while in the other it is 27·3%. Show that this data is in agreement with the law of multiple proportions.
Weight percent of carbon = 42.9
Weight percent of oxygen = 100 - 42.9 = 57.1
In second compound:
Weight percent of carbon = 27.3
Weight percent of oxygen = 100 - 27.3 = 72.7
Now in first compound:
57.1 parts by weight of oxygen combine with 42.9 parts by weigh of carbon
 1 part by weight of oxygen will combine with
1 part by weight of oxygen will combine with
Now in second compound:
72.7 parts by weight of oxygen combine with 27.3 parts by weight of carbon
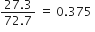 parts of carbon.
parts of carbon.The weights of carbon which combine with same weights of oxygen in two compounds bear a ratio 0·751 : 0·375 or 2 : 1. This is a simple ratio. Hence, the data illustrates the law of multiple proportion.
Define the law of reciprocal proportion. Explain with suitable examples.
The law of reciprocal proportion (Richtev 1792) states that if two elements A and B combine separately with another element C, then the ratio of respective weights of A and B which combine with a fixed weight of C is the same or simple multiple of the weights in which A and B combine with each other. For example, sodium and chlorine combine with hydrogen to form compounds NaH and HCl respectively.
In NaH:
23 g sodium combines with 1 g hydrogen.
In HCl:
35·5 g chloride combines with 1 g hydrogen.
The ratio of masses of sodium and chlorine which combine with a fixed mass of hydrogen (1 g) is 23 : 35·5
Now sodium and chlorine also combine to form NaCl.
In NaCl:
23g sodium combines with 35·5 chlorine in the ratio 23 : 35·5
This is the same ratio which combines with one part of hydrogen in NaH and HCl.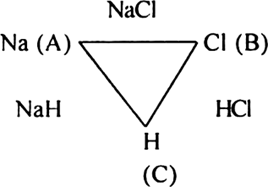
Show that the law of reciprocal proportions is proved by the following results:
1·4g of the element A is known to combine with 1·6g of element B, while 0·5g of another element C combines with 3·5g of the element A and 2·857g of the element C combines with 22·857g of element B.
(i) In AB compound:
1.4 g of A combines with 1.6g of B![]() 1 g of A combines with
1 g of A combines with 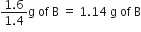
(ii) For AC compound:
3.5 g of A combines with 0.5g of C
1g of A combines with 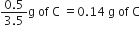
Ratio of masses of B (in AB) and C(in AC) that combines with the fixed mass of A(1 g) is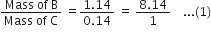
(iii) In BC compound:
Ratio of masses of B and C, when they combine to form BC is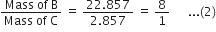
Since the two ratios (1) and (2) between the masses of B and C are same, hence the law of reciprocal proportion is proved.
State Gay Lussac’s law of combining volumes. Illustrate with suitable examples.
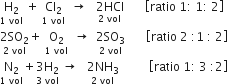
The volume ratio in the above examples is a simple whole number ratio.
Two volumes of hydrogen combine with one volume of oxygen to produce two volumes of steam. Show that this illustrates Gay Lussac’s law.
Given that 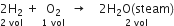
The ratio in the volumes of gases are 2:1:2 (simple ratio). Hence, it illustrates the Gay-Lussac's law.
Give various postulates of Dalton's atomic theory.
The main postulates of Dalton’s atomic theory (Dalton 1808) are:
1. Matter is made up of very small indivisible particles called atoms.
2. Atoms of the same element are identical in all respects.
3. Atoms of different elements differ in properties and mass.
4. Atoms combine in a simple but fixed ratio to form compound atoms (now called molecules).
5. Atom is the smallest particle which can take part in a chemical reaction.
6. Atom can neither be created nor destroyed during a chemical reaction.
7. Atoms of two elements may combine in different ratios to form more than one compound.
What are the limitations of Dalton's atomic theory?
Limitations of Dalton's atomic theory:
1) It could not make any distinction between an ultimate particle of an element and that of a compound both of which are loosely called atoms, the former known as simple atoms and the latter known as compound atoms.
2. It could not explain Berzelius hypothesis.
3. It could not explain the Gay Lussac’s law of combining volumes.
4. It could not explain as to why the atoms of different elements combine to form compound atoms.
5. It failed to explain the cause of chemical combination.
6. It failed to give the idea of isotopes and isobars.
How Dalton's atomic theory was modified on the basis of modern reseraches? or Give various postulates of modern atomic theory.
On the basis of new experimental facts, Dalton’s atomic theory has been modified as:
1. Atom is no longer indivisible. Atom is composed of still smaller particles which are called electrons, protons and neutrons.
2. Atoms of same element may not have same atomic mass. For example, some atoms of chlorine have atomic mass 35 amu while others have atomic mass 37 amu. Such atoms of same element having different atomic masses are called isotopes.
3. Atoms of different elements may have same atomic masses. For example, atomic mass of calcium and argon atoms are 40 amu. Such atoms of different elements having same atomic mass are called isobars.
4. There are no compound atoms but these are called molecules. Atom is the smallest particle that takes part in a chemical reaction.
5. The ratio in which atoms of different elements combine may not be simple e.g. in a molecule of sugar (C12H22O11), the ratio of C,H and O atoms is 12 : 22 : 11 which is not simple.
6. Atoms of one element can be transmuted into atoms of other elements (Discovery of artificial transmutation).
7. Atom is no longer considered indestructible. In nuclear reaction, during the conversion of atoms of one substance into the atoms of other substance, some of the mass is lost and converted into energy according to the relation E = mc2 (Einstein equation) where E = energy, m = mass and c is the, velocity of light (3×108 ms–1). Hence, in nuclear reaction atoms get destroyed and their mass changes into energy.
What do you understand by atom and molecule?
Molecule: Molecule is the smallest particle of a substance (element or compound) which is capable of independent existence. The molecules are formed by the combination of two or more atoms. In case the atoms happen to be the same, the molecules are called homoatomic molecules (e.g. O2, N2, H2 etc.). In case atoms happen to be different, the molecules are known as heteroatomic molecules (e.g. NH3, CO2, SO2 etc.).
What is the difference between molecule of an element and molecule of a compound?
Molecule of an element: Molecule of an element contains two or more atoms of the same element. For example, a molecule of hydrogen consists of two atoms of hydrogen. Such molecules are called diatomic molecules. A molecule of ozone (O3) contains three atoms of oxygen. The molecules of noble gases such as helium, neon, argon, krypton and xenon are regarded as mono atomic molecules. This is because each molecule of these gases contains only one atom.
Molecule of a compound: Molecule of a compound contains two or more atoms of the different elements. For example, a molecule of water (H2O) contains two atoms of hydrogen and one atom of oxygen. Molecules of some of the natural products are quite complex and contain a very large number of atoms. For example a molecule of cane sugar (C12H22O11) contains 45 atoms.
Define Avogadro’s law. Taking a suitable example, prove that it is not in contradiction with Dalton’s atomic theory.
Avogadro’s law states that ‘equal volumes of all gases under similiar conditions of temperature and pressure contain equal number of molecules.’
On applying Avogadro’s law to the reaction between hydrogen and oxygen to form water vapours, we have,
Hydrogen + Oxygen  Water vapours
Water vapours
2 volumes 1 volume 2 volumes(experimental)
2n molecules n molecules 2n molecules
(Avogadro's hypothesis)
2 moleucles + 1 molecule  2 molecules
2 molecules
1 molecule + 1/2 molecule  1 molecule
1 molecule
This means that one molecule of water is made of 1 molecule of hydrogen and 1/2 molecule of oxygen (i.e. one atom of oxygen). Since the molecules can be subdivided, the result is not in conflict with Dalton’s atomic theory.
Explain breifly the present state of Atomic-Molecular theory of matter.
It can be summarized as follows:
1. Matter is made up of extremely small particles called molecules which may have independent existence. Molecules themselves are composed of two or more atoms. However, molecules of noble gases are composed of one atom only.
2. Molecules of a particular substance are identical in all respects such as mass, size, shape and other properties.
3. Molecules of different substances have different masses, sizes, shapes and other properties.
4. Molecular mass of a substance is the sum of the atomic masses of the constituent atoms.
5. During a chemical reaction, the molecules of the reacting substances first break into atoms and then recombine to form new molecules of the products.
6. The number of atoms present in one molecule of an element is known as atomicity of the element.
Define the following:
Precision and accuracy
Define the following:
Unit factor
1 min = 60 s
1 = Conversion factor =

Define the following:
Average atomic mean.
Average atomic mass : The average atomic mass is defined as “the average relative mass of an atom of an element as compared to the mass of carbon atom (C-12) taken as 12 amu.’ For example, in naturally occurring neon isotopes and their relative abundance are as follows :
|
Isotope |
Fractional abundance |
|
20Ne |
0·9051 |
|
21Ne |
0·0027 |
|
22Ne |
0·0922 |
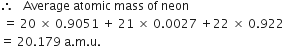
What do you understand by:
(i) Atomic Mass?
(ii) Gram atomic mass(gram-atom)?
 It is therefore, called relative atomic mass.
It is therefore, called relative atomic mass. Thus, Relative atomic mass

The term average is used in the definition because atoms of the same element may have different atomic masses (isotopes) and hence an average value is taken. For example, there are two isotopes of chlorine having atomic masses 35 and 37 respectively. These isotopes occur in chlorine in the ratio 3:1, thus, Average atomic mass of chlorine
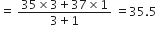
(ii) Gram atomic mass(gram-atom). It is the quantity of an element whose mass in grams is numerically equal to its atomic mass on amu scale. In other words, atomic mass of an element in grams is called gram atomic mass. It is also called gram atom. For example,
Atomic mass of hydrogen (1 gram atom of hydrogen) = 1·008 g
Atomic mass of oxygen (1 gram atom of oxygen) = 16 g
Atomic mass of sodium (1 gram atom of sodium) = 23 g
Number of gram atoms and mass in grams of an element are related by the following relation:
No. of gram-atoms = 
Calculate the atomic mass(average) of chlorine using the following data:
| %Natural Abundance | Molar mass | |
| 35Cl | 75·77 | 34·9689 |
| 37Cl | 24·23 | 36·9659 |
Molar mass = 34.9689
Fractional abundance of 37Cl = 0.2423
Molar mass = 36.9659
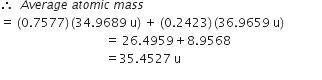
Use the data given in the following table to calculate the molar mass of naturally occurring argon isotopes:
Isotope Isotopic molar mass Abundance
36Ar 35·96755 g mol–1 0·337%
38Ar 37·96272 g mol–1 0·063%
40Ar 39·9624 g mol–1 99.600%
Molar mass of Ar = 35.96755 x 0.00337 + 37.96272 x 0.0063 + 39.9624 x 0.99600
[0.121 +0.024+39.802] = 39.948 g mol-1
What do you mean by Atomic mass unit?
Atomic mass unit. The quantity ![]() of an atom of carbon (C12) is known as atomic mass unit. The atomic mass unit equals to 1·6603 × 10–27 kg.
of an atom of carbon (C12) is known as atomic mass unit. The atomic mass unit equals to 1·6603 × 10–27 kg.
Calculate the volume at STP occupied by:
(i) 16 g of oxygen
(ii) 2·5 moles of CO2
(iii) 1 × 1021 molecules of oxygen.
Gram molecular mass of oxygen = 32 g
Now 32 g oxygen at STP occupies volume = 22.4 litres
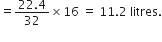
(ii) 2.5 moles of CO2
1 mole of carbondioxide at STP occupies = 22.4 litres
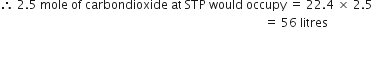
(iii)


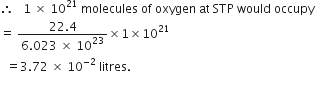
If 1021 molecules are removed from 200 mg of CO2, then how many moles of CO2 are left?
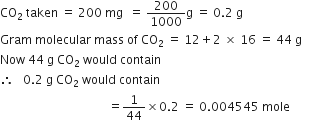
Since
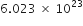 molecules are present in 1 mole of CO2
molecules are present in 1 mole of CO2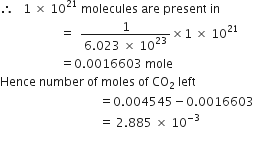
What is the name of the element whose mass of one atom is 4×10–23. Given Avogadro’s number as 6×1023.
One atom of an element weighs
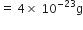
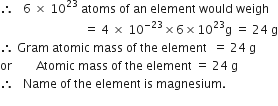
Explain the terms empirical and molecular formulae of a compound. How are these related to each other?
Empirical formula: The empirical formula is the formula of a compound which gives the simple whole number ratio of the atoms of various elements present in one molecule of the compound. For example, empirical formula of benzene is CH, which indicates that atomic ratio of C : H in benzene is 1 : 1.
Molecular formula: The formula which represents the actual number of atoms of various elements present in the molecule of a substance is known as molecular formula.
For example, the molecular formula of benzene is C6H6 which shows that in one molecule of benzene there are actually six carbon atoms and six hydrogen atoms.
Relation between empirical and molecular formulae:
Molecular formula is a whole number multiple of empirical formula and the two are related as:
Molecular formula = n × (Empirical formula) where n is an integer 1, 2, 3 .... and is given by
How will you calculate the empirical formula mass?
What is the percentage of carbon, hydrogen and oxygen in ethanol?
Molar mass of ethanol (C2H5OH)
= 2(12.01) +6(1.008) +16.00 = 46.068g
Mass percentage of carbon
=
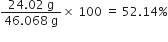
Mass percentage of hydrogen
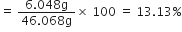
Mass percentage of oxygen
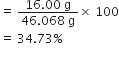
Calculate the mass percentage of different elements present in sodium sulphate (Na2SO4).
Molecular mass of sodium =23
Molecular mass of sulphur =32
Molecular mass of oxygen =16
Thus,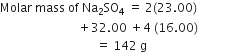
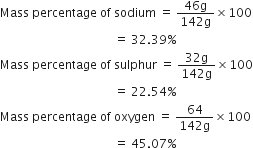
Fe2(SO4)3 is the empirical formula of a crystalline compound of iron. It is used in water and sewage treatment for the removal of suspended impurities. Calculate the mass percentage of iron, sulphur and oxygen in the compound.
Molecular mass of 
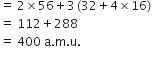
Percentage of iron

Percentage of sulphur
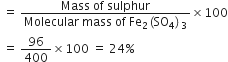
Percentage of oxygen
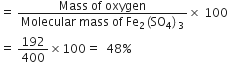
What is the empirical formula of the compounds having molecular formula as:
(i) C6H6
(ii) C6H12
(iii) H2O2
(iv) H2O
(v) Na2CO3
(vi) B2H6
(vii) N2O6
(i) C6H6: The empirical formula is CH.
(ii) C6H12: The empirical formula is CH2.
(iii) H2O2: The empirical formula is HO2.
(iv) H2O: The empirical formula is H2O.
(v) Na2CO3: The empirical formula is Na2CO3
(vi) B2H6: The empirical formula is BH3.
(vii) N2O6: The empirical formula is NO3.
Determine the empirical formula of an oxide of iron which has 69·9% iron and 30.1% dioxygen by mass.
|
Element |
Percentage |
Atomic Mass |
Atomic ration |
Simplest ratio |
Simplest whole number ratio |
|
Iron (Fe) |
69.9 |
55.85 |
69.9/55.85=1.25 |
1.25/1.25 =1 |
2 |
|
Oxygen (O) |
30.1 |
16.00 |
30.1/16.00=1.88 |
1.88/1.25=1.5 |
3 |
Empirical formula Fe2O3
Silicon (Si = 28) forms a compound with chlorine (Cl = 35·5) in which 5·6g of silicon is combined with 21·3g of chlorine. Calculate the empirical formula of the compound.
(i) To calculate the percentage of silicon and chlorine:
Weight of silicon = 5.6 g
Weight of chlorine = 21.3 g![]()
(ii) To calculate the empirical formula:
| Element | % | atomic no. | atomic ratio | simplest ratio | simple whole ratio |
| Silicon | 20.8 | 28 | 20.8/28=0.74 | 0.74/0.74=1 | 1 |
| Chlorine | 79.2 | 35.5 | 79.2/35.5=2.23 | 2.23/0.74=3 | 3 |
Therefore empirical formula is SiCl3.
2.38 g of uranium was heated strongly in a current of air. The resulting oxide weighed 2806 g. Determine the empirical formula of the oxide. (At. mass of U = 238, O = 16).

(ii) To calculate the empirical formula of the oxide:

Four grams of copper chloride on analysis was found to contain 1·890 g of copper (Cu) and 2·110 g of chlorine (Cl). What is the empirical formula of copper chloride?

(ii) To calculate the empirical formula of the compound.

The atomic mass of metal M is 56. Calculate the empirical formula of its oxide containing 70% of M.
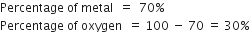
(ii) To calculate the empirical formula of oxide:

A chemical compound is found to have the following composition: C = 19·5%, Fe = 15·2%, N = 22·8%, K = 41·5%. Calculate the empirical formula of the compound. What will be the molecular formula if the molecular mass of the compound is 368? Name the compound also.
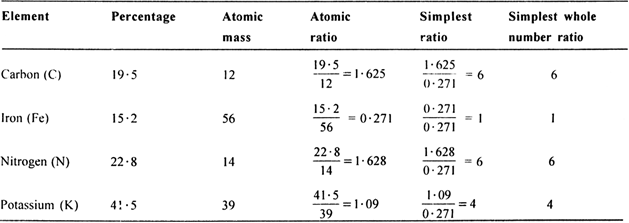
Empirical formula of the compound

(ii) To calculate the molecular formula of the compound:
Empirical formual mass = 6 x 12 + 56 +6 x 14 + 4 x 39
= 72+56+84+156
=368 (given)
Molecular mass = 368
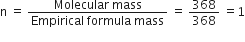
Hence molecular formula is

Name of compound is Potassium ferrocyanide.
A compound on analysis, is found to have the following composition:
(i) Sodium = 14·31%, (ii) Sulphur = 9·97
(iii) Oxygen = 69·50% (iv) Hydrogen = 6·22%.
Calculate the molecular formula of the compound assuming that whole of hydrogen in the compound is present as water of crystallisation. Molecular weight of the compound is 322.

(ii) To calculate the molecular formula of the compound.
Empirical formula mass of,
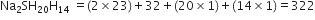
Molecular mass = 322 [given]
Hence,

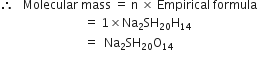
Whole of the hydtogen is present in the form of water. Thus, 10 water molecules are present in the molecule.
So molecular formula of the compound is Na2SO410H2O.
A sample of hydrazine consists of 87·42% N and 12·58% H by mass. The molecular mass of hydrazine is 32·0 g mol–1. Calculate its molecular formula.
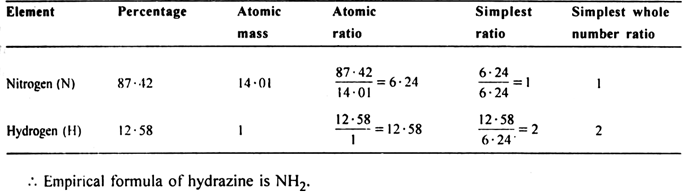
(ii) To calculate the molecular formula:
Empirical formula mass
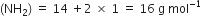
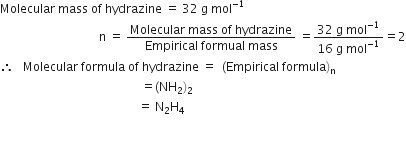
Naphthalene (moth balls) contains 93·71% carbon and 6·29% hydrogen. If its molar mass is 128 g mol–1, calculate its molecular formula.

(ii) To calculate the molecular formula:
Empirical formual mass
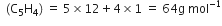
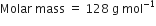 [given]
[given]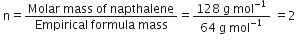

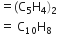
A welding fuel gas contains carbon and hydrogen only. Burning a small space of it in oxygen gives 3.38 g carbon dioxide, 0·690g of water and no other products. A volume of 10·0L (measured at STP) of this welding gas is found to weigh 11·6g. Calculate: (i) empirical formula (ii) molar mass of the gas and (iii) molecular formula.
i.1mole(44g) of CO2 contains 12g of carbon.
3.38 g of CO2 will contain carbon = (12g/44g) x3.38g =0.9217g
18g of water contains 2g of hydrogen
Therefore 0.690g of water will contain hydrogen=2g/18gx 0.690 =0.0767 g
Since carbon and hydrogen are the only constituents of the compounds, the total mass of the compounds is:
=0.9217+0.767
=0.9984g
Thus,
Percent of C in the compound = (0.9217/.9984) x100 =92.32%
Percent of H in the compound =(0.0767/0.9984) x100=7.68%
Moles of carbon in the compound =92.32/12.00 =7.69
Moles of hydrogen in the compound= 7.68/1=7.68
Since, ration of carbon to hydrogen in the compound=7.69:7.68=1:1
Hence, the empirical formula of the gas is CH.
ii) Given,
Weight of 10.0L of the gas (at S.T.P)=11.6 g
Therefore, weight of 22.4L of gas at STP =(11.6/10.0L) x22.4L
=25.984g
Hence, the molar mass of the gas is 26.0 g.
iii) Empirical formula mass of CH =12+1 =13g
n= molar mass of gas/empirical formula mass of gas
n=26/13
n=2
Therefore, molecular formula of gas= (CH)n
=C2H2
Butyric acid contains only C, H and O, 4.24mg sample of butyric acid is completely burnt. It gives 8.45mg of carbon dioxide and 3.46mg of water. What is the mass percentage of each element in butyric acid?

Percentage of H.
Percentage of O.
If the elemental composition of butyric acid is found to be 54.2%C, 9.2%H and 36.6%O, determine the empirical formula.

The molecular mass of butryic acid was determined by experiment to be 88 amu. what is the molecular formula?
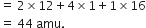
Molecular mass = 88 amu [given]
Hence,

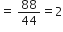
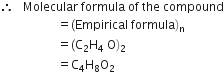
What is a chemical equation? What are the essentials of a chemical equation?
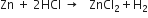 .
.Essentials of a chemical equation.A chemical equation must satisfy the following conditions:
(i) It should represent a true chemical change i.e. the change represented by the chemical equation should be practically possible.
For example, the equation

is not a true chemical equation since copper does not react with sulphuric acid to produce copper sulphate and hydrogen.
(ii) It should be arithmetically balanced.
Atoms of each element on both the sides of the arrow

is an arithmetically balanced equation.
(iii) It should be molecular. If any elementary gas takes part in a chemical equation it must be expressed in the molecular form e.g.
What are the implications of a chemical equation?
Or
What informations are conveyed by a chemical equation?
A chemical equation gives a lot of information viz.,
1. It tells the names of the reactants and products.
2. It tells the relative number of molecules of reactants and products.
3. It tells the relative number of moles of reactants and the products.
4. It tells the relative weights of reactants and the products.
5. It tells the relative volumes of reacting gases and those of products formed in case of gaseous reactants. For example, the chemical equation.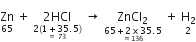
conveys the following information:
1. Zinc reacts with hydrochloric acid to produce zinc chloride and hydrogen.
2. One atom of zinc reacts with two molecules of hydrogen chloride to produce one molecule of zinc chloride and one molecule of hydrogen.
3. One mole of zinc reacts with two moles of hydrogen chloride to produce one mole of zinc chloride and one mole of hydrogen.
4. 65 gram of zinc reacts with 73 gram of hydrochloric acid to give 136 gram of zinc chloride and 2 gram of hydrogen.
5. 22·4 litres of hydrogen is produced at S.T.P. when one mole of zinc reacts with 2 moles of hydrogen chloride.
What are the limitations or drawbacks of a chemical equation?
A chemical equation does not give any information regarding:
1. The physical states of the reactants and the products, whether these are solids, liquids, gases or in the form of solution.
2. In case of solution, their concentration i.e. whether concentrated or dilute.
3. The time taken for the completion of the reaction.
4. Whether any heat is absorbed or given out during the chemical change.
5. The speed of a chemical reaction, whether it is slow or fast.
6. The conditions of temperature, pressure or catalyst etc. at which the reaction takes place.
How can we make a chemical equation more informative?
Or
How can we remove the drawbacks or limitations of a chemical equation?
The drawbacks of a chemical equation can be partially removed or we can make a chemical equation more informative as follows:
1. By specifying the physical states of the reactants and products in a chemical equation by putting the letter (s) for solid, (l) for liquid and (g) for gaseous state after the formula of the substance. The word (aq), which means aqueous solution, is used when the substance is in the form of solution, For example, reaction between sodium and water to form sodium hydroxide solution and hydrogen gas may be written as:
2. The concentrations of the reactants used in the form of solution can be shown by the word dil. for dilute and conc. for concentrated e.g.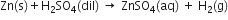
3. By using a down arrow  for the compound precipitated and an upward arrow
for the compound precipitated and an upward arrow  for a gas evolved. For example,
for a gas evolved. For example,
(i) Evolution of hydrogen gas.
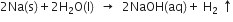
(ii) Precipitation of AgCl.

4. By mentioning the condition of reaction such as heat (), pressure, catalyst on the arrow head.
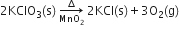
5. In case of exothermic reactions, the sign "+ heat" is written along with the products.
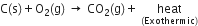
In case of enodthermic reactions, the sign "-heat" is written along with products. 
Explain the following terms with examples:
1. Skeleton equation
2. Balanced equation
3. Thermochemical equation.
For example, consider the reaction of cupric oxide with ammonia to produce copper, nitrogen and water. The skeleton equation is

2. Balanced equation. It is a chemical equation representing a true chemical change in which the number of atoms of various elements on both the sides of the arrow
 For example, balanced equation representing the reaction between cupric oxide and ammonia is
For example, balanced equation representing the reaction between cupric oxide and ammonia is
3. Thermochemical equation. A chemical equation which includes the heat changes taking place during the reaction is called thermochemical equation.
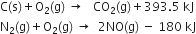
What do you mean by 'balancing a chemical equation'? On what principle the balancing of a chemical equation is based?
For example,

How are chemical equations balanced? discuss any two.
The methods generally used for balancing equations are:
1. The hit and trial method
2. Partial equation method
3. Oxidation number change method
4. Ion- electron method.
1. The hit and trial method: This method is used to balance simple equations. This method involves the following steps:
(i) Write the symbols and formulae of the reactants and products in the form of skeleton equation.
(ii) Select the element which occurs at the minimum number of places on the two sides. Make number of its atoms equal on both the sides of the equation by multiplying the formula by a suitable number.
(iii) The element which occurs at maximum number of places should be balanced last of all.
(iv) Balance the atoms of elementary gases last of all.
(v) When all the atoms are balanced, make the equation molecular by multiplying the equation by a suitable number.
2. Partial equation method: This method is used for balancing complicated equations. This method involves the following steps:
(i) Split the chemical equation into two or more stages.
(ii) Write simple equation for different stages and balance by hit and trial method. These equations are called partial equations.
(iii) All the step-wise equations (partial equations) are added to get the balanced equation.
Balance the following equations:![]()

P occurs at maximum places and should be balanced last of all.
(i) To balance O atom, multiply H3PO4 by 4 and H3PO4 by 3.

(ii) P and H atoms are automatically balanced.
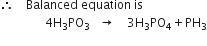
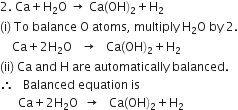
Translate the following equations into the language of chemistry and balance by hit and trial method:
Magnesium nitride + Water  Magnesium hydroxide + Ammonia
Magnesium hydroxide + Ammonia

(ii) To equalise the number of Mg atoms, multiply the molecule Mg(OH)2 by 3.

(iii) To balance the nitrogen atoms, multiply the molecule NH3 by 2.

(iv) To equalise the number of H and O atoms on both the sides of the above equation, multiply HO by 6.
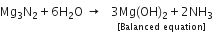
Balance the following skeleton equation by hit and trial method:![]()
(ii) To equalise the number of atoms of Fe and O on both side, multiply Fe by 3 and the molecule H2O by 4.
(iii) To equalise hydrogen atom, multiply H atom by 8 on L.H.S.

(iv) Making the equation molecular to get the balanced equation,
Balance the following skeleton equation by hit and trial method:![]()
(ii) To balance Fe atoms, multiply Fe(OH)3 by 2.
(iii) To balance S atoms, multiply (NH4)2SO4 by 3.
(iv) To balance N atoms, multiply NH3 by 6.
(v) To balance H and O atoms, multiplyng H2O by 6, we get.
This is the balanced equation.
Balance the following skeleton equation:
(i) Skeleton equation is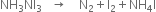
(ii) Change the equation into atomic form.![]()
(iii) To balance H atoms, multiply NH3NI3 by 4 and NH4I by 3.![]()
(iv) To balance I atoms, multiply I by 9 on the R.H.S.![]()
(V) To balance N atoms, multiply N by 5 on the R.H.S.![<pre>uncaught exception: <b>Http Error #404</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php line 61<br />#0 [internal function]: com_wiris_plugin_impl_HttpImpl_0(Object(com_wiris_plugin_impl_HttpImpl), NULL, 'http://www.wiri...', 'Http Error #404')
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('com_wiris_plugi...', Array)
#2 [internal function]: _hx_lambda->execute('Http Error #404')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(532): call_user_func_array(Array, Array)
#4 [internal function]: haxe_Http_5(true, Object(com_wiris_plugin_impl_HttpImpl), Object(com_wiris_plugin_impl_HttpImpl), Array, Object(haxe_io_BytesOutput), true, 'Http Error #404')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('haxe_Http_5', Array)
#6 [internal function]: _hx_lambda->execute('Http Error #404')
#7 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(27): call_user_func_array(Array, Array)
#8 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(444): com_wiris_plugin_impl_HttpImpl->onError('Http Error #404')
#9 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(458): haxe_Http->customRequest(true, Object(haxe_io_BytesOutput), NULL, NULL)
#10 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(40): haxe_Http->request(true)
#11 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(80): com_wiris_plugin_impl_HttpImpl->request(true)
#12 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#13 {main}</pre>](/application/zrc/images/qvar/CHEN11084578-5.png)
(vi) Change the elementary gases into molecular form, by multiplying the equation by 2![]()
Balance the following skeleton equation:
(i) Skeleton equation is
(ii) Change the equation into atomic form.![]()
(iii) To balance the number of oxygen atoms on both sides, multiply H2O by 4.![]()
(iv) To balance hydrogen atoms on both sides, multiply the molecules of HCl by 8.![]()
(v) To balance chlorine atoms on both sides, multiply the chlorine atom on the R.H.S. by 5.![]()
(vi) Change the elementary gases into molecular form, by multiplying the equation by 2.![]()
This is a balanced equation.
Balance the given skeletion equation ![]() by partial equation method.
by partial equation method.
It involves the following steps:
(i) Nitric acid decomposes to liberate nascent oxygen.![]() ...(1)
...(1)
(ii) Nascent oxygen reacts with phosphorus to form phosphorus pentoxide.![]() ...(2)
...(2)
(iii) ![]() dissolves in water to form phosphoric acid.
dissolves in water to form phosphoric acid.![]() ...(3)
...(3)
Balancing the partial equations by hit and trial methods,
![]()
![]() ...(5)
...(5)
![]() ...
...
(6)
Multiplying the partial equations (4) and (6) by 10 and 2 respectively and adding all the three equations, we have,
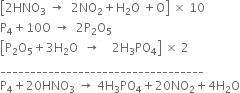
Balance the following equation by partial equation method:![]()
(i) Reaction between
(ii)
Multiplying (2) by 5 and adding the equations,
Balance the following equation by partial equation method:![]()
(i) Nitric acid decomposes to liberate nascent oxygen.
(ii) Nascent oxygen reacts with copper to form cupric oxide.
(iii) Cupric oxide combines with nitric acid to form cupric nitrate.
Adding all the partial equation (1), (2) and (3), we get the balanced equation as
Balance the given skeletion equation ![]() by partial equation method.
by partial equation method.
It involves the following steps:
(i) Reaction between KMnO4 and H2SO4 to liberate nascent oxygen. ...(1)
...(1)
(ii) Oxalic acid is oxidised to CO2 and water by the nascent oxygen.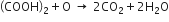 ...(2)
...(2)
Multiplying equation (2) by 5 and adding partial equations,
Balance the given skeleton equation by partial equation method:

It involves the following steps:
(i) Chlorine reacts with water to form hydrochloric acid and hypochlorous acid.
![]() ...(1)
...(1)
(ii) Hydrochloric acid then reacts with sodium hydroxide to give sodium chloride and water.![]() ...(2)
...(2)
(iii) Hypochlorous acid reacts with sodium hydroxide to give sodium hypochlorite and water.![]() ...(3)
...(3)
(iv) Sodium hypochlorite decomposes to give sodium chlorate.![]()
Multiply the partial equations (1), (2) and (3) by 3 and add all the four equations.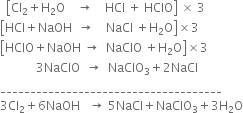
Balance the following equations by partial equation methods:
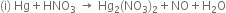
![<pre>uncaught exception: <b>Http Error #404</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php line 61<br />#0 [internal function]: com_wiris_plugin_impl_HttpImpl_0(Object(com_wiris_plugin_impl_HttpImpl), NULL, 'http://www.wiri...', 'Http Error #404')
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('com_wiris_plugi...', Array)
#2 [internal function]: _hx_lambda->execute('Http Error #404')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(532): call_user_func_array(Array, Array)
#4 [internal function]: haxe_Http_5(true, Object(com_wiris_plugin_impl_HttpImpl), Object(com_wiris_plugin_impl_HttpImpl), Array, Object(haxe_io_BytesOutput), true, 'Http Error #404')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('haxe_Http_5', Array)
#6 [internal function]: _hx_lambda->execute('Http Error #404')
#7 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(27): call_user_func_array(Array, Array)
#8 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(444): com_wiris_plugin_impl_HttpImpl->onError('Http Error #404')
#9 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(458): haxe_Http->customRequest(true, Object(haxe_io_BytesOutput), NULL, NULL)
#10 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(40): haxe_Http->request(true)
#11 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(80): com_wiris_plugin_impl_HttpImpl->request(true)
#12 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#13 {main}</pre>](/application/zrc/images/qvar/CHEN11084597-1.png)
...(1)
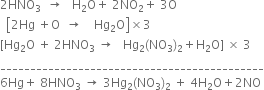
(ii)
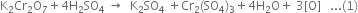
Multiplying equation (2) by 3 and add the two equations
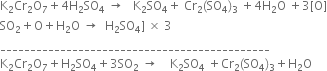
Balance the following equations:![]()
Multiplying equation (1) by 16 and add the two equations.
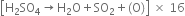
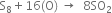
---------------------------------------------
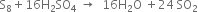
Balance the following equations:![]()
Multiplying equaton (1) by 5 and adding these three equations.

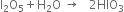
______________________________
Balance the following equations:
Multiplying equation (1) by 4 and adding the three equations.
How many types of problems are based on chemical equations?
The problems based on chemical equations are of three types:
1. Involving mass-mass relationship.
2. Involving mass-volume relationship.
3. Involving volume-volume relationship.
In order to solve the problems based on chemical equations, keep the following points in mind:
1. Write down the balanced chemical equation.
2. Write down the moles or gram atomic or gram molecular masses of the substances whose quantities are given or have to be found out. In case, there are two or more atoms or molecule of a substance, multiply the gram atomic or gram molecular mass or moles by the number of atoms or molecules.
3. If the volume of a gas is involved in the equation, write down 22·4 litres at S.T.P. below the formula in place of gram molecular mass.
4. Write down the actual quantities of the substances given. For the substances where weights/volumes have to be calculated, just write the sign of interrogation (?) for that.
5. Calculate the result by unitary method.
How many grams of barium sulphate are obtained when 26 g of barium chloride reacts with enough sulphuric acid? (Atomic mass of Ba = 137).
BaCl2 + H2SO4
1 mole 1 mole
137 + (2 x 35.5) 137 + 32 + (4 x 16)
208 g 233 g
26 g ?
Stoichiometry indicates that 208 g BaCl2 gives 233 g BaSO4
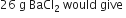
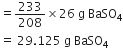
How many litres of oxygen at S.T.P. will be required to burn completely 2.2 g of propane?
C3H8 + 5O2
1 mole 5 x 22.4L
44 g at STP
Stoichiometry indicates that
1 mole (44 g) propane
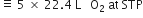
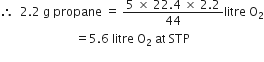
Calculate the amount of KClO3 needed to supply sufficient oxygen for burning 112L CO gas at S.T.P.
The balanced chemical equations repersenting the reactions are:
![]()
2CO + O2 ![]() 2CO2
2CO2
2 moles
(2 x 22.4L at STP)
Stoichiometry indicates that,![]()
or 2 x 22.4 L CO at S.T.P.
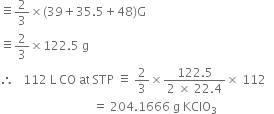
How many moles of oxygen can be obtained by the decomposition of 1 mole of potassium chlorate in the following reaction:
How many moles of reactants are needed for obtaining 1 mole of oxygen?
2KClO3(s)
2 moles 3 moles
Stoichiometry indicates that:
2 moles KClO3 on decomposition give
= 3 moles of oxygen
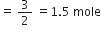
Again 3 moles of oxygen are produced from 2 moles of KClO3.
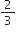 moles of KClO3 = 0.66 mol
moles of KClO3 = 0.66 molGastric juice contains 3g HCl per litre. If a person produces 2.5 L of gastric juice per day, how many antacid tablets each containing 400 mg of Al(OH)3 are needed to neutralise all the HCl produced in one day?
Al(OH)3 + 3HCl
27+3(16+1) 3 x 36.5
=78(g) =109.5
Mass of HCl produced per day = 3 x 2.5 = 7.5 g
Stoichimetry indicates that 109.5 g HCl is neutralised by 78 g Al(OH)3
7.5 g HCl is neutralised by
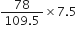
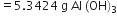
Now 400 mg or

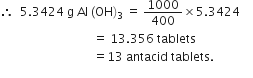
Calculate the quantity of lime required to soften 60000 litres of well water containing 16.2 g of calcium carbonate per hundred litre.
Ca(HCO3)2 + Ca(OH)2
(40+2+24+96) (40+32+2)
= 162 g = 74 g
16.2 g ?
(i) To calculate the weight of calcium bicarbonate present.
Weight of calcium bicarbonate present in 100 litres of well water = 16.2 g, Now 100 L well water contains
= 16.2 g Ca(HCO3)2
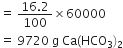
(ii) To calculate the quantity of lime required. Stoichiometry indicates that 162 g Ca(HCO3)2 requires 74 g Ca(OH)2
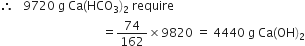
KBr (potassium bromide) contains 32·9% by weight of potassium. If 6·40 g of bromine reacts with 3·60 g of potassium, calculate the number of moles of potassium which combines with bromine to form KBr.
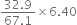
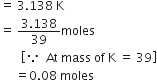
Thus, Br will be limiting reactant and K left unreacted
= (3.60 - 3.13) g
= 0.462 g
Decomposition of NaHCO3 takes place at 270°C. In a sample containing Na2CO3 and NaHCO3, the heating at 270°C results in the loss of 10% by weight. What is the percentage composition of the sample?
2NaCHO3
2x(23+1+12+48) 2+16 12 + 2 x16
= 168 g = 18 g = 44 g
Stoichiometry indicates that loss of 62 g of mass takes place from 168 g of NaHCO3. So loss of 10 g of mass takes place from
Thus the percentage of
and percentage of Na2CO3 in the sample
= 100 - 27.1 = 72.9%
How much potassium chlorate should be heated to produce 2.24 L of oxygen at NTP?
2KClO3
2 moles 3 moles
2(39+35.5+48) 3 x 22.4 L
= 245 g (at NTP)
Stoichiometry indicates that
3 x 22.4L oxygen is produced from 245g KClO3
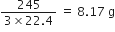
If ten volumes of dihydrogen gas react with five volumes of dioxygen gas, how many volumes of water vapour could be produced?

2 volumes of H2 react with 1 volume of O2 to produce 2 volumes of water vapours.
∴ 10 volumes of H2 react with 5 volumes of O2 to produce 10 volumes of water vapours.
What volume of oxygen at STP is required to affect complete combustion of 200 cm3 of acetylene and what would be the volume of carbondioxide formed?
(i) To calculate the volume of O2 at STP required to effect complete combustion of 200 cm3 of acetylene:
According to Gay Lussac’s law of gaseous volumes,
2 volumes C2H2 will require O2 for complete combustion = 5 vol
= 500 cm3 at STP
Thus volume of O2 required = 500 cm3 at S.T.P.
(ii) To calculate the volume of CO2 produced at S.T.P
According to Gay Lussac’s law of gaseous volumes.
2 volumes of C2H2 produce CO2 = 4 vol
What do you mean by limiting reagent?
suppose 2 moles of H2 are reacted with 2 moles of O2 to form water. According to the above balanced chemical equation. 2 moles of H2 require 1 mole of O2 for complete reaction. Therefore, there should be 4 moles of H2 to react with 2 moles of O2 but H2present is only 2 moles. Hence, H2 is a limiting reagent which will get used up earlier when only 1 mole of O2 would react leaving behind 1 mole of unreacted oxygen.
Calculate the amount of carbon dioxide that could be produced when
(i) 1 mole of carbon is burnt in air.
(ii) 1 mole of carbon is burnt in 16g of dioxygen.
(iii) 2 moles of carbon are burnt in 16g of dioxygen.
C(s) + O2 (g)
1 mol 1 mol 1 mol
(12g) (32 g) (44 g)
(i) Since in air, the combustion is complete, therefore when 1 mole of carbon is burnt, the amount of CO2 formed is 44g.
(ii) Since 16g of dioxygen is available, therefore it can combine only with 0.5 mole of carbon. Thus, dioxygen is the limiting reactant and O2 produced is 22g.
(iii) Here again, dioxygen is the limiting reactant. 16g of O2 can combine with 0.5 mole of carbon. Thus CO2 produced is 22g.
96g of SO2 reacts with 29·0g of O2 to yield SO3. Which is the limiting reactant?
2SO2 + O2
2 mol 1 mol 2 mol
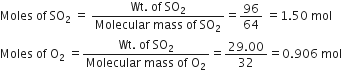
Stoichiometry indicates that 2 mol SO2 required O2 = 1 mol
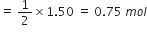
But moles of O2 actually present = 0·906 mol Therefore, O2 is in excess and SO2 is the limiting reactant.
In a reaction![]()
Identify the limiting reagent, if any, in the following reaction mixtures.
(i) 300 atoms of A + 200 molecules of B
(ii) 2 mol A + 3 mol B
(iii) 100 atoms of A + 100 molecules of B
(iv) 5 mol A + 2-5 mol B
(v) 2·5 mol A + 5 mol B
According to the given reaction:
(i) 1 atom of A will react with molecules of B2 = 1
300 atoms of A will react with molecules of B2 = 300
But molecules of B2 actually available = 200
∴ B2 is the limiting reactant.
(ii) 1 mol of A reacts with 1 mol of B
∴ 2 mol of A will react with 2 mol of B.
Hence A is the limiting reactant.
(iii) 100 atoms of A will react with 100 molecules of B. Hence there are no limiting reactants.
(iv) 2·5 mol of B will react with 2·5 mol of A. Hence B is the limiting reagent.
(v) 2·5 mol of A will react with 2·5 mol of B.
Hence A is the limiting reagent.
Chlorine is prepared in the laboratory by treating manganese dioxide (MnO2) with aqueous hydrochloric acid according to the reaction![]()
How many grams of HCl react with 5.0 g of manganese dioxide?
1 mol [55+2 x16=87 g] MnO2 reacts completely with 4 mol [4x 36.5=146g] of HCl
Therefore,
5.0 g of MnO2 will react with
=(146/87) x5.0g of HCl
=8.4 g of HCl
Hence, 8.4g of HCl will react completely with 5.0g of manganese dioxide.
Calcium carbonate reacts with aqueous HCl to give CaCl2 and CO2 according to the reaction,

What mass of CaCO3 is required to react completely with 25 mL of 0·75M HCl?
= 0.75 x 36.5
= 27.375 g
= 0.684 g
The reaction is
CaCO3(s) + 2HCl(aq)
1 mol 2 mol
40+12+48 2 x 36.5
= 100 g = 73 g
? 0.684 g
Now 73 g of HCl are required to react with 100g of CaCO3
Zinc and hydrochloric acid react according to the reaction:![]()
If 0.30 mol Zn are added to hydrochloric acid containing 0.52 mol HCl, how many moles of H2 are produced?
Stoichiometry shows that
2 mol of HCl need 1 mol Zn
But moles of Zn acutally present = 0.52 mol.
Therefore, Zn is in excess and HCl is the limiting reagent.
Now 2 mol HCl forms H2 = 1 mol
Dinitrogen and dihydrogen react with each other to produce ammonia according to the following chemical equation:
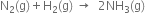
(i) Calculate the mass of ammonia produced if 2·00 × 103 g dinitrogen reacts with 1·00×103 g of dihydrogen.
(ii) Will any of the two reactants remain un reacted?
(iii) If yes, which one and what would be its mass?
Thus, N2 in the limiting reagent while H2 is the excess reagent
2 mol of N2 i.e. 28g of N2 produce NH3
= 2 mol = 2 x 17 = 34g
NH3 =
(ii) H2 will remain unreacted.
(iii) Mass of H2 that remains unreacted = 1000 - 428.6 = 571.4 g.
Define mass percent or weight percent.
It is the amount of solute in grams present in 100g of the solution. Mathematically,
Mass percent = 
Define normality and molarity.

Molarity (M). It is defined as the number of moles of solute dissolved per litre of the solution.

Define molality and mole fraction.

Mole fraction. Mole fraction may be defined as the ratio of the number of moles of one component to the total number of moles of all the components present in the solution.
For a binary solution made up of components A and B,
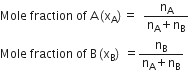
Sum of the mole fractions
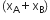

Calculate the molarity of NaOH in the solution prepared by dissolving its 4g in enough water to form 250mL of the solution.

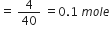
Volume of solution = 250 mL
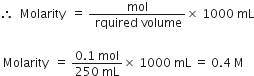
Calculate the normality of a solution containing 0.5 g NaOH in 250 mL of solution.
Gram equivalent is given as =
Gram equivalent of NaOH = 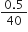
Volume of solution = 250 mL
Normality is given as =
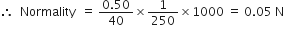
How many moles of NaOH are contained in 27mL of 0.15 M NaOH?
1000mL of NaOH contains 0.15 moles![]() 27 mL of NaOH contains
27 mL of NaOH contains 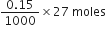
= 0.004 moles
What is the concentration of sugar (C12H22O22) in mol L–1 if its 20g are dissolved in enough water to make a final volume up to 2L?
Molar mass of sugar 
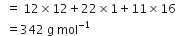
Number of moles of sugar = 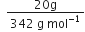
= 0.0585 mol![]() Molar concentration (molarity)
Molar concentration (molarity)

How are 0.50 mol Na2CO3 and 0·50 M Na2CO3 different?
Molar mass of Na2CO3 = 2 x 23 + 12 + 3 x 16 = 106 g
0.50 mol Na2CO3 means 0.50 x 106g = 53g
0.50M Na2CO3 means 0.50 mol i.e. 0.50 x 106g, i.e. 53 g of Na2CO3 are present in 1 litre of the solution.
Calculate the mass of sodium acetate (CH3COONa) required to make 500 mL of 0·375 molar aqueous solution. Molar mass of sodium acetate is 82·0245g mol–1.
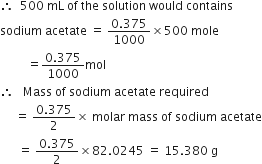
In a reaction vessel 0.184 g of NaOH is required to be added for completing the reaction. How many millilitre of 0.150 M NaOH solution should be added for this requirement?
Molar mass of NaOH = 40 g mol-1![]() 1000 mL of NaOH solution contains 0.150 mol = 0.150 x 40 = 6 g
1000 mL of NaOH solution contains 0.150 mol = 0.150 x 40 = 6 g
It means that 6g sodium hydroxide is present in 1000 mL
![]() 0.184 g sodium hydroxide would be present in
0.184 g sodium hydroxide would be present in
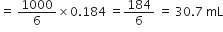
Commercially available concentrated hydrochloric acid contains 38% HCl by mass.
(i) What is the molarity of the solution (density of solution = 1·19g cm-3)?
(ii) What volume of concentrated HCl is required to make 1·0L of 0·10 M HCl?
Volume of solution
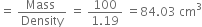
Moles of HCl =
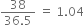
Molarity =

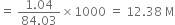
(ii) By applying normality equation,
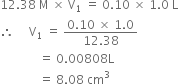
What volume of 9M HCl and 4 MHCl should be mixed to get 1L of 5M HCl solution?
Applying molarity equation, we have,

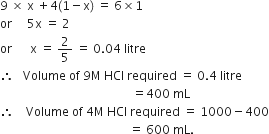
If the density of methanol is 0·793 kg L–1, what is its volume needed for making 2·5L of its 0·25 M solution?
Molar mass of methanol (CH3OH)
= 12 + 4 x 1 + 16 = 32g mol-1
= 0.032 kg mol-1![]() Molarity of the given solution
Molarity of the given solution
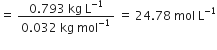
Applying the molarity equation,
(Given solution) 

or 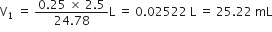
Calculate the molarity of a solution of ethanol in water in which the mole fraction of ethanol is 0.040.(assume the density of water to be one).
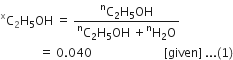
Our aim is to find the number of moles of ethanol in 1L of the solution which is nearly = 1L of water.
Number of moles in 1L of water
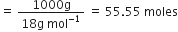
Substituting the values of
 in eq. (1) we have
in eq. (1) we have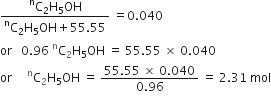
Hence molarity of the solution = 2.31 M
Calculate the concentration of nitric acid in moles per litre in a sample which has a density, 1.41 g mL–1 and the mass per cent of nitric acid in it being 69%.
We have given,
Mass percent of nitric acid in the sample =69%
Thus, 100g of nitric acid contains 69g of nitric acid by mass.
Molar mass of nitric acid contains 69g of nitric acid by mass.
Molar mass of nitric acid (HNO3)
=[1+14+3(16)]
=1+14+48
=63g mol-1
Therefore, number of moles in 69g of HNO3
= 69g/63g mol-1
=1.095 mol
Volume of 100g of nitric acid solution =
=Mass of solution/density of solution
= 100/1.41g ML-1
=70.92mL =70.92 x10-3L
Concentration of nitric acid
=1.095mole/70.92 mol L-1
Thus,
Concentration of nitric acid =15.44 mol/L
Determine the molecular formula of an oxide of iron in which the mass per cent of iron and oxygen are 69.9 and 30.1 respectively.
We have given,
Mass percent of iron (Fe) =69.9%
Mass percent of oxygen (O)=30.1%
Number of moles of iron present in the oxide =69.90/55.85 =1.25
Number of moles of oxygen present in the oxide=30.1/16.0
=1.88
Ratio of iron to oxygen in the oxide,
1.25:1.88
=1:1.5
=2:3
Therefore the empirical formula of the oxide is Fe2O3.
Empirical formula mass of Fe2O3= [2(55.85) +3(16)]g
Molar mass of Fe2O3=159.69g
Thus, n= Molar mass/Empirical Formula mass =159.69/159.7g
=0.999 = 1(approx.)
Molecular formula of a compound is obtained by multiplying the empirical formula with n. Thus, the empirical formula of the given oxide is Fe2O3 and n is 1.
Hence, the molecular formula of the oxide is Fe2O3.
A sample of drinking water was found to be severely contaminated with chloroform, CHCl3, supposed to be carcinogenic in nature. The level of contamination was 15 ppm (by mass).
(i) Express this is percent by mass.
(ii) Determine the molality of chloroform in the water sample.
i) 1ppm is equivalent to 1 part out of 1 million (106) parts.
Therefore, mass percent of 15 ppm chloroform in water
= (15/106) x100 =1.5 x 10-3 %
ii) 100 g of the sample contains 1.5 x 10-3 g of CHCl3.
1000 g of the sample contains 1.5 x 10-2 g of CHCl3
Thus, Molality of chloroform in water
= 1.5 x 10-2 g/Molar mass of CHCl3
Molar mass of CHCl3 =12+1+3(35.5)
=119.5 g mol-1
Therefore, molality of chloroform in water =0.0125 x 10-2 m
=1.25 x 10-4 m
Calculate the mass of nitrogen supplied to the soil by 5Kg of urea [CO(NH2)2]?
The formula for urea is.
The molar mass for urea is 14x 2+1x 4+12+16= 60 g/mole.
In this 60 g of urea, nitrogen has a mass of 28 g.
So by simple proportion in 5 kg of urea,
nitrogen has a mass =
Calculate the molar mass of the following:
H2O
Molecular mass of H2O = Mass of oxygen + Mass of hydrogen.
mass of hydrogen =1.008 amu
mass of oxygen =16.000 amu
2(1.008 amu) + 16.000 amu = 18.016 amu
Calculate the molar mass of the following:
CO2
Molecular mass of CO2 = Mass of carbon +Mass of oxygen.
Mass of carbon =12.01
Mass of oxygen=16.00
12.01 amu +2 x (16.00 amu) = 44.01 amu.
Calculate the molar mass of the following:
CH4
Molar mass of CH4 = Mass of carbon +mass of hydrogen.
Mass of carbon =12.01
Mass of hydrogen =1.008
12.01 amu + 4x(1.008 amu) = 16.042 amu
Calculate the molecular mass of glucose (C6H12O6) molecule.
Molecular mass of glucose (C6H12O6) =Mass of carbon +mass of hydrogen +mass of oxygen
Mass of carbon =12.011amu
Mass of oxygen=16.00 amu
Mass of hydrogen=1.008 amu
= 6(12.011 amu) +12 (1.008 amu) + 6(16.00 amu)
= 72.066 amu + 12.096 amu + 96.00 amu
= 180.162 amu
Calculate the gram molecular mass of sugar (C12H22O11).
Mass of carbon =12g
Mass of oxygen=16g
Mass of hydrogen= 1g
Molecular mass of sugar (C12H22O11)
= 12 x (At. mass of carbon) + 22 x (At. mass of hydrogen) + 11 x (At. mass of oxygen)
= 12 x 12 + 22 x 1 +11 x 16 = 342 amu![]() Gram molecular mass of C12H22O11 = 342 g
Gram molecular mass of C12H22O11 = 342 g
How much copper can be obtained from 100 g of copper sulphate (CuSO4)?
1 mole of CuSO4 contains 1 g atom of Cu.
Now molar mass of CuSO4 = 63.5 + 32 + 4 x 16 =159.5 g mol-1
Cu that can be obtained from 159.5 g of CuSO4 = 63.5 g![]() Cu that can be obtained from 100 g of CuSO4
Cu that can be obtained from 100 g of CuSO4
= ![]() = 39.81 g
= 39.81 g
Explain the term 'mole'?
The unit of amount of substance is mole which contains 6 · 023 × 1023 entities. These entities may be atoms, molecules, ions, electrons or any other entity. This number 6·023 × 1023 is called Avogadro’s number and is symbolised as N.
A mole is defined as the amount of any substance which contains Avogadro’s number (6·023 × 1023) of particles (atoms, molecules or formula units) of that substance and has a mass equal to gram atomic mass, gram molecular mass or gram formula mass as the case may be e.g.,
1 mole of oxygen atom
= 6.023 x 1023 atoms = 16 g
1 mole of oxygen molecules
= 6.023 x 1023 molecules = 32 g
1 mole of water molecules
= 6.023 x 1023 molecules = 18 g
1 mole of sodium chloride
= 6.023 x 1023 formula units
= 58.5 g
1 mole of electrons = 6.023 x 1023 electrons
Mole in terms of volume: In the case of gases, it has been found that the volume occupied by one mole of any gas at STP (0°C and 1-atmosphere pressure) is 22·4 litres. The volume occupied by 1 mole of gas at STP is known as gram molecular volume (G.M.V.) or molar volume.
1 mole of gas = 22.4 litres of gas at STP
For example,
1 mole of H2 = 22.4 litres of H2 at STP
1 mole of O2 = 22.4 litres of O2 at STP
Thus,
1 mole = 6.023 x 1023 particles (i.e. atoms, molecules, formula units, ions, etc.)
= Gram atomic mass (gram atoms),
gram molecular mass (gram molecules), gram formula mass, etc.
= 22.4 litres at STP in case of gases.
What is the utility of mole concept?

2. To calculate the mass of one molecule of the substance.

3. To calculate the number of atoms and the number of molecules in a given mass of the element.
The Number of atoms in a given mass of the element.
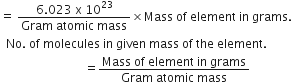
4. To calculate the number of molecules and the number of moles in a given mass of the substance.
No. of molecules in a given mass of a substance
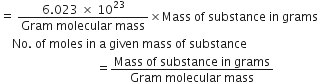
5. To calculate the volume occupied at S.T.P. by a given mass of a gas.
Volume occupied at S.T.P. by given mass of a gas

6. To calculate the number of molecules present in a given volume of a gas at S.T.P.
No. of molecules contained in given volume of gas at S.T.P.

7. To calculate the number of atoms and molecules in the given number of moles of a substance.
No. of atoms in a given number of moles of element
= 6 · 023 × 1023 × No. of moles of element No. of molecules in a given number of moles of substance
= 6·023 × 1023 × No. of moles of substance
Calculate the mass of:
(i) an atom of sodium
(ii) in a single molecule of water.
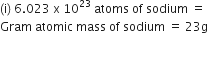
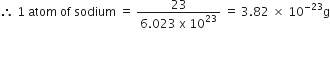
(ii) Gram molecular mass of H2O = 18 g
Now 6.023 x 1023 molecules of water have mass = 18 g.
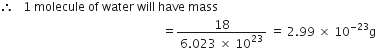
In three moles of ethane (C2H6), calculate the following:
Number of moles of carbon atoms.
In three moles of ethane (C2H6), calculate the following:
Number of moles of hydrogen atoms.
 3 mole of C2H6 would contain 6 x 3 i.e. 18 moles of H atoms.
3 mole of C2H6 would contain 6 x 3 i.e. 18 moles of H atoms. In three moles of ethane (C2H6), calculate the following:
Number of molecules of ethane.
How many sulphur atoms are present in each of the following quantities
(i) 4.5 mole of S
(ii) 6 mole of S8 ?
(i) 1 mole of S = 6.023 x 1023 atoms of sulphur
4.5 mole of S = 4.5 x 6.023 x 1023 atoms of sulphur
= 2.71 x 1024 atoms of sulphur
(ii) 1 mole of S8 = 6.023 x 1023 molecules of S8
= 8 x 6.023 x 1023 atoms of sulphur![]() 6 mole of S8 = 6 x 8 x 6.023 x 1023 atoms of sulphur
6 mole of S8 = 6 x 8 x 6.023 x 1023 atoms of sulphur
= 2.89 x 1025 atoms of sulphur
How many atoms and molecules of phosphorus are present in 62 g of phosphorus (P4)?
Molecular formula of phosphorus = P4
Gram molecular mass of phosphorus (P4)
= 4 x 31 = 124 g
124 g of phosphorus contains 6.023 x 1023 molecules of phosphorus
![]() 62 g of phosphorus would contain
62 g of phosphorus would contain

Calculate the number of molecules present:
(i) in one drop of water having mass of 0.05 g
(ii) in 34.20 gram of cane sugar (C12H22O11).
(i) 1 mole of H2O = 18 g
= 6.023 x 1023 molecules
Mass of 1 drop of water = 0.05 g
Now 18 g of H2O contains 6.023 x 1023 molecules
![]() 0.05 g of
0.05 g of ![]() would contain
would contain
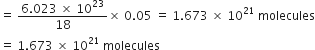
(ii) Molecular mass of ![]()
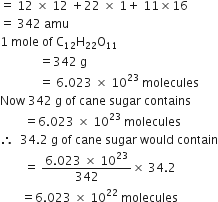
Calculate the number of atoms of each kind in 5·3 g of Na2CO3.
Formula mass of Na2CO3
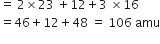
Gram formula mass of Na2CO3 = 106 g
Now 106 g of Na2CO3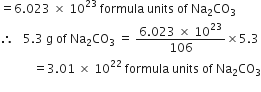
Now one formula unit of Na2CO3 contains 2 atoms of sodium, 1 atom of carbon and 3 atoms of oxygen.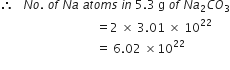
No of carbon atoms in 5.3 g of ![]()

No. of oxygen atoms in 5.3 g of ![]()
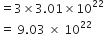
What is the number of molecules of CO2 present that contains 8g of O2?
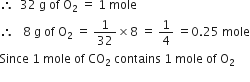

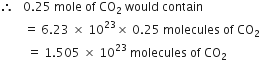
What weight of Ca will contain the same number of atoms as are present in 3.2g of sulphur?
Atomic mass of sulphur = 32 amu
Gram atomic mass of sulphur = 32 g
1 mole of sulphur contains = 6.023 x 1023 atoms
Now 32 g of sulphur contains
= 6.023 x 1023 atoms
3.2 g of sulphur would contain
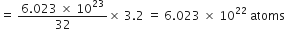
Gram atomic mass of calcium = 40 g
1 mole of calcium = 40 g
= 6.023 x 1023 atoms
Now 6.023 x 1023 atoms of calcium have mass = 40 g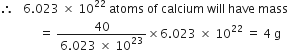
0.01 mole of a compound weighs 1 g. Calculate the molecular mass of the compound.
0.01 mole of a compound high = 1 g
1 mole of a compound would weigh
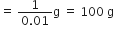

Calculate the number of atoms in each of the following;
(i) 52 moles of Ar
(ii) 52 u of He
(iii) 52 g of He.
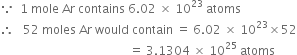
(ii) 52u of He.
Atomic mass of He = 4u
i.e. 4u of He = 1 atom He
(iii) 52 g of He.
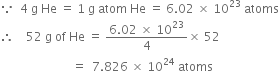
Which one of the following will have largest number of atoms?
- 1g Au (s)
- 1g Na (s)
- 1g Li (s)
- 1 g of Cl2(g)
C.
1g Li (s)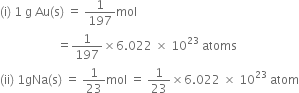
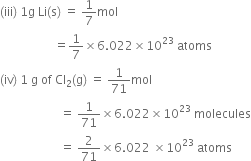
Hence 1 g Li(s) has the largest number of atoms
The cost of table salt (NaCl) is Rs 8 per kg. Calculate its cost per mole.
= 23 + 35.5 = 58.5 g mol-1
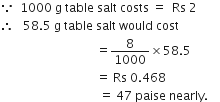
The molecular formula of a commercial resin used for exchanging ions in water softening is C8H7SO3Na ( mol. wt = 206). What would be the maximum uptake of Ca2+ ions by the resin when expressed in mole per gram resin?
-
1/103
-
1/206
-
2/309
-
1/412
D.
1/412
We know the molecular weight of C8H7SO3Na
= 12x8+1x7+32+16x3+23 = 206
we have to find mole per gram of resin
therefore,
1 g of C8H7SO3Na has number of mole
=1/206 mol
Taking the reaction,
C8H7SO3Na + Ca2+ → (C6H7SO3)2Ca + 2Na+
therefore, 2 moles of C8H7SO3Na combines with 1 mol of Ca2+
Thus, 1 mole of C8H7SO3Na will combine with 0.5 mol of Ca2+
Hence, 1/206 mole of C8H7SO3Na will combine with,
0.5 x (1/206)mol of Ca2+ = 1/412 mol Ca2+
In Carius method of estimation of halogens, 250 mg of an organic compound gave 141 mg of AgBr. The percentage of bromine in the compound is: (at. Mass Ag = 108; Br = 80)
-
24
-
36
-
48
-
60
A.
24
Weight of Organic compound = 250 mg
Weight of AgBr = 141 mg
therefore, According to the formula of % of bromine by Carius method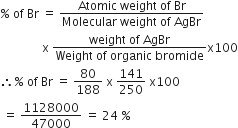
A gaseous hydrocarbon gives upon combustion 0.72 g of water and 3.08 g of CO2.The empirical formula of the hydrocarbon is
-
C2H4
-
C3H4
-
C6H5
-
C7H8
D.
C7H8
18 g H2O contains 2gH
therefore, 0.72 g H2O contains 0.08 g H
44 g CO2 contains 12 g C
therefore, 3.08 g CO2 contains 0.84 g C
∴ C:H = 0.84/12: 0.08/1
+ 0.07 : 0.08 = 7:8
∴Empirical formula = C7H8
Experimentally it was found that a metal oxide has formula M0.98O. Metal M, is present as M2+ and M3+ in its oxide. The fraction of the metal which exists as M3+ would be:
-
7.01%
-
4.08%
-
6.05%
-
5.08%
B.
4.08%
Metal oxide = M0.98O
If ‘x’ ions of M are in +3 state, then
3x + (0.98 – x) × 2 = 2
x = 0.04
So the percentage of metal in +3 state would be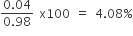
The most abundant element by mass in the body of a healthy human adult are :
Oxygen (61.4%) ; Carbon (22.9%), Hydrogen(10.0%) ; and Nitrogen (2.6%). The weight which a 75 kg person would gain if all 1H atoms are replaced by 2H atoms is
-
15 kg
-
37.5 Kg
-
7.5 Kg
-
40 Kg
C.
7.5 Kg
Mass in the body of a healthy human adult has :-
Oxygen = 61.4%, Carbon = 22.9%,
Hydrogen = 10.0% and Nitrogen = 2.6%
Total weight of person = 75 kg
Mass due to 1H is =
(10/100)x 75 = 7.5kg
1H atoms are replaced by 2H atoms.
So mass gain by person =7.5 kg
The ratio of mass percent of C and H of an organic compound (CXHYOZ) is 6: 1. If one molecule of the above compound (CXHYOZ) contains half as much oxygen as required to burn one molecule of compound CXHY completely to CO2 and H2O. The empirical formula of compound CXHYOZ is
C2H4O3
C3H6O3
C2H4O
C3H4O2
A.
C2H4O3
The ratio of mass % of C and H in CxHyOz is 6: 1.
Therefore,
The ratio of mole % of C and H in CxHyOz will be 1: 2.
Therefore x : y = 1 : 2, which is possible in options 1, 2 and 3.
Now oxygen required to burn CxHy
Now z is half of the oxygen atoms required to burn CxHy
Now putting values of x and y from the given options:
Option (1), x = 2, y = 4
In the Kjeldahl's method for estimation of nitrogen present in a soil sample, ammonia evolved from 0.75 g of sample neutralised 10 mL of 1 M H2SO4.The percentage of nitrogen in the soil is
-
37.33
-
45.33
-
35.33
-
43.33
B.
45.33
In Kjeldahl's method, percentage of N is given by
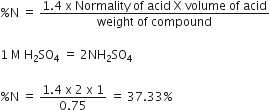
How many grams of the concentrated nitric solution should be used to prepare 250 mL o 2.0M HNO3 ? The concentrated acid is 70% HNO3.
-
45.0 g conc. HNO3
-
90.0 g conc. HNO3
-
70.0 g conc. HNO3
-
54.0 g conc. HNO3
A.
45.0 g conc. HNO3
Given, molarity of solution = 2
Volume of solution = 250 mL = 250/1000 = 1/4 L
Molar mass of
HNO3 = 1+14+3 x 16 = 63 g mol-1
therefore, Molarity
= 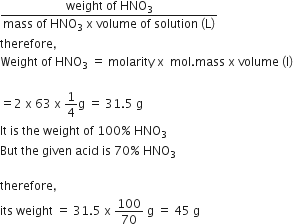
Mole fraction of the solute in a 1.00 molal aqueous solution is
-
0.0177
-
0.0344
-
1.7700
-
0.1770
A.
0.0177
1.00 molal aqueous solution = 1.0 mole in 1000 g water nsolute = 1; Wsolvent = 1000g
nsolvent = 1000/18 = 55.56
Xsolute = 1/ 1+ 55.56 = 0.0177
Which one of the following statements is not true?
-
Concentration of DO below 6 ppm is good for the growth of fish
-
Clean water would have a BOD value of less than 5 ppm
-
Oxides of sulphur, nitrogen and carbon are the most widespread air pollutant
-
pH of drinking water should be between 5.5 - 9.5
A.
Concentration of DO below 6 ppm is good for the growth of fish
The growth of fish is inhibited if the concentration of DO is below 6 ppm.
If Avogadro number NA, changed from 6.022 x 1023 mol-1 this would change
-
the definition of mass in units of grams
-
the mass of one mole of carbon
-
the ratio of chemical species to each other in the balanced equation
-
the ratio of elements to each other in a compound
B.
the mass of one mole of carbon
If Avogadro number NA, is changed from 6.022 x 1023 mol-1 to 6.022 x 1020 mol-1 this would change the mass of one mole of carbon.
therefore,
1 mole of carbon has mass = 12 g
or 6.022 x 1023 atoms of carbon have mass = 12 g
therefore, 6.022 x 1020 atoms of carbon have mass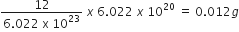
20.0 g of a magnesium carbonate sample decomposes on heating to give carbon dioxide and 8.0 g magnesium oxide. What will be the percentage purity of magnesium carbonate in the sample? (Atomic weight of Mg =24)
-
75
-
96
-
60
-
84
D.
84
In the given problem we have a practical yield of MgO. For calculation of percentage yield of MgO. we need a therortical yield of MgO. For this, we shall use mole concept.
MgCO3(s) → MgO (s) + CO2(g) .. (i)
What is the mass of precipitate formed when 50 mL of 16.9% solution of AgNO3 is mixed with 50 mL of 5.8% NaCl solution?
(Ag = 107.8, N = 14, O = 16, Na = 23, Cl = 35.5)
-
28 g
-
3.5 g
-
7 g
-
14 g
C.
7 g
For the calculation of the mass of AgCl precipitate, we find the mass of AgNO3 and NaCl in equal volume with the help of mole concept. 16.9% solution of AgNO3 means 16.9 g AgNO3 is present in 100 mL solution.
therefore, 8.45 g AgNO3 will present in 50 mL solution similarly,
5.8 g NaCl is present in 100 ml solution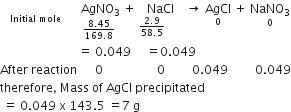
The number of water molecules is maximum in
-
18 molecules of water
-
1.8 g of water
-
18 g of water
-
18 moles of water
D.
18 moles of water
Mole is the biggest unit to measure the number of molecules/atom/ions.
therefore,
1 mole of water contains molecules = 6.02 x 1023
therefore, 18 moles of water contain molecules
= 18 x 6.02 x 1023 molecules
Now, 1 mole of water = 18 g of water
= 6.02 x1023
and 1.8 g of water contains = 6.02 x 1022 molecules.
Which has the maximum number of molecules among the following?
-
44 g CO2
-
48 g O3
-
8 g H2
-
64 g SO2
A.
44 g CO2
44 g CO2 = 1 mol CO2 = NA molecules of CO2
48 g O3 = 1 mol O3 = NA molecules of O3
8 g H2 = 4 mol H2 = 4 x NA molecules of H2
64 g SO2 = 1 mol SO2 = NA molecules of SO2
The number of atoms in 0.1 moles of a triatomic gas is (NA = 6.02 x 1023 mol-1)
-
6.026 x 1022
-
1.806 x 1023
-
3.600 x 1023
-
1.800 x 1022
B.
1.806 x 1023
Number of atoms = number of moles x NA x atomicity
= 0.1 x 6.02 x 1023 x 3
= 1.806 x 1023 atoms
10 g of hydrogen and 64 of oxygen were filled in a steel vessel and exploded. Amount of water produced in this reaction will be
-
2 mol
-
3 mol
-
4 mol
-
1 mol
C.
4 mol
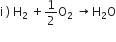
Amount of water produced is decided by limited reactant (ie, the reactant which is used in small amount)
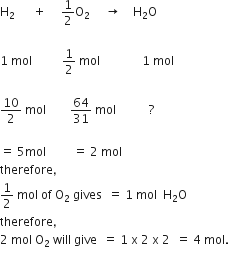
An Organic compound contains carbon, hydrogen and oxygen. Its elemental analysis gave C, 38.71% and H, 9.67%. The empirical formula of the compound would be
-
CH3O
-
CH2O
-
CHO
-
CH4O
A.
CH3O
| Element | % | At. wt | Relative no. of atoms | Simplest ratio of atoms |
| C | 38.71 | 12 | 3.23 | 3.23/3.23 = 1 |
| H | 9.67 | 1 | 9.67 | 9.67/3.23 = 3 |
| O | 51.62 | 16 | 3.23 | 3.23/3.23 |
Hence empirical formula is CH3O.
How many moles of lead (II) chloride will be formed from a reaction between 6.5 g of PbO and 3.2 g of HCl?
-
0.044
-
0.333
-
0.011
-
0.029
D.
0.029
The reagent which is present in smaller quantity is called the limiting reagent and the moles of product depends on it and number of moles
=
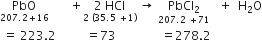
Here, 1 mole of PbO reacts with 2 moles of HCl, thus PbO is the limiting reagent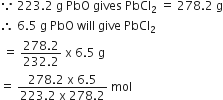
0.029 mol
An element, X has the following isotopic composition;
200X: 90%
199X : 8.0%
202X ; 2.0 %
The weighted average atomic mass of the naturally -occurring element X is closet to:
-
200 amu
-
201 amu
-
202 amu
-
199 amu
A.
200 amu
Weight of 200X = 0.90 x 200 = 180.00 amu
Weight of 199X = 8.08 x 199 = 15.92 amu
Weight 0f 202X = 0.02 x 202 = 4.04 amu
Total weight = 199.06 = 200 amu
Mock Test Series
Sponsor Area
Sponsor Area