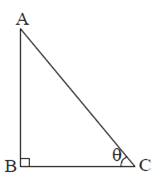
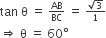गणित Chapter 6 त्रिभुज
Sponsor Area
NCERT Solution For Class 10 गणित गणित
निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ (ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।
समरूप: वर्ग, वृत्त, समबाहु त्रिभुज।
विषमरूप: आयत, अन्य त्रिभुज।
बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:
नहीं है। क्योंकि कोणों का माप समान नहीं है।
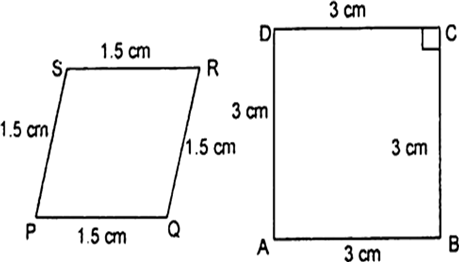
आकृत (i) और (ii) में,  है। (i) में EC और (ii) में AD ज्ञात कीजिए:
है। (i) में EC और (ii) में AD ज्ञात कीजिए:
 [ दिया है ]
[ दिया है ]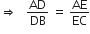
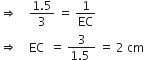
(ii) ∆ABC में,
 [ दिया है ]
[ दिया है ]

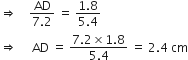
किसी  की भुजाओं PQ और PR पर क्रमश: बिंदु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
की भुजाओं PQ और PR पर क्रमश: बिंदु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या EF || QR है:
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm और FR = 2.4 cm
(ii) PE = 4 cm, QE = 4.5 cm. PF = 8 cm और RF = 9 cm
(iii) PQ = 1.28 cm. PR = 2.56 cm, PE = 0.18 cm और PF = 0.36 cm
किसी की भुजाओं PQ और PR पर क्रमश: बिंदु E और F स्थित हैं। निम्नलिखित में से प्रत्येक स्थिति के लिए, बताइए कि क्या है:औरऔरऔर
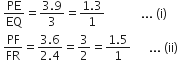
समीकरण (i) और (ii) से, हम प्राप्त करते हैं
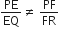
नहीं, क्योंकि
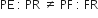
(ii) हम प्राप्त करते हैं,
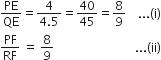
समीकरण (i) और (ii) से, हम प्राप्त करते हैं
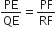
 हाँ, क्योंकि PQ:PR=PE:PF
हाँ, क्योंकि PQ:PR=PE:PF(iii) हम प्राप्त करते हैं,
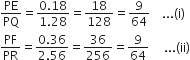
समीकरण (i) और (ii) से, हम प्राप्त करते हैं
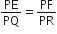
 हाँ, क्योंकि PQ:PR=PE:PF
हाँ, क्योंकि PQ:PR=PE:PF
आकृति में यदि LM||CB और LN||CD हो तो सिद्ध कीजिए कि 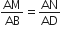 है।
है।
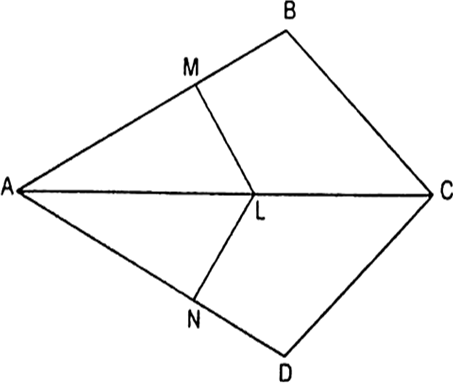
LM||CB

∆ADC में,
LN||CD


समीकरण (i) और (ii) से
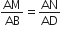 यह सिद्ध हुआ
यह सिद्ध हुआ
आकृति में DE||AC और DF||AE है। सिद्ध कीजिए कि 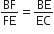 है।
है।
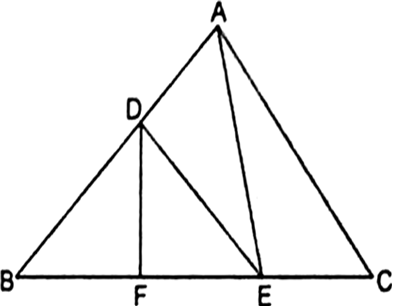
सिद्ध करना है:
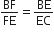
∆ABE में,
DF||AE

∆ABC में,
DE||AC

समीकरण (i) और (ii) की तुलना करने पर, हमें प्राप्त होता है:
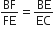 यह सिद्ध हुआ
यह सिद्ध हुआ
आकृति में DE||OQ और DF||OR है। दर्शाइए कि EF||QR है।
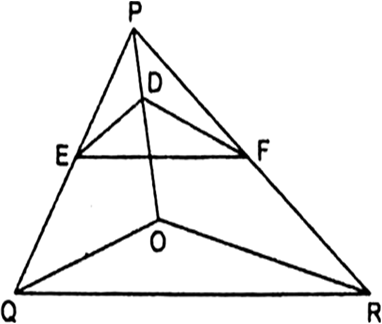
DE||OQ
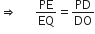 ...(i)
...(i)∆POR में,
DF||OR
 ...(ii)
...(ii)समीकरण और की तुलना करने पर, हम प्राप्त करते हैं
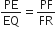
∴ EF||QR यह सिद्ध हुआ
आकृति में क्रमश: OP, OQ और OR पर स्थित बिंदु A, B और C इस प्रकार हैं कि AB||PQ और AC||BC है। दर्शाइए कि BC||QR है।
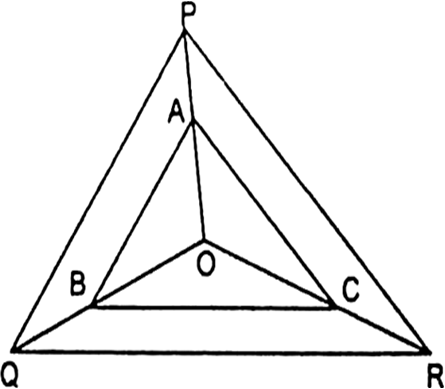
AB||PQ
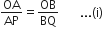
∆OPR में,
AC||PR

समीकरण (i) और (ii) की तुलना करने पर, हमें प्राप्त होता है

BC||QR
प्रमेय 6.1 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की एक भुजा के मध्य-बिंदु से होकर दूसरी भुजा के समांतर खींची गई रेखा तीसरी भुजा को समद्विभाजित करती है। (याद कीजिए कि आप इसे कक्षा IX में सिद्ध कर चुके हैं।)
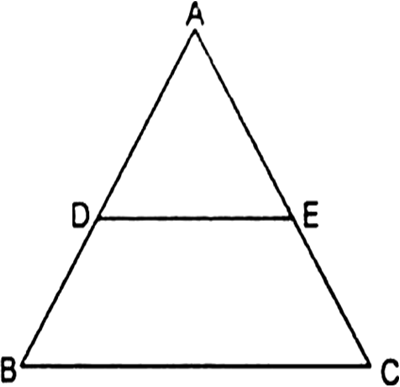
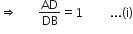
∆ABC में,
DE||BC

समीकरण (i) और (ii) की तुलना करने पर, हमें प्राप्त होता है


प्रमेय 6.2 का प्रयोग करते हुए सिद्ध कीजिए कि एक त्रिभुज की किन्हीं दो भुजाओं के मध्य-बिंदुओं को मिलाने वाली रेखा तीसरी भुजा के समांतर होती है। (याद कीजिए कि आप कक्षा IX में ऐसा कर चुके हैं।)
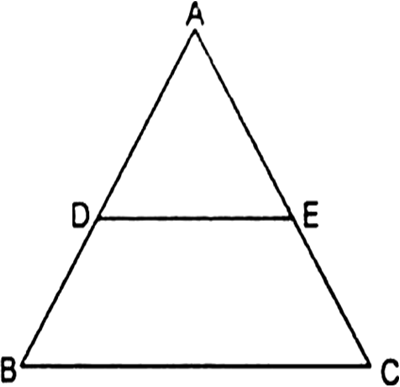
AD = DB
 ...(i)
...(i)AE = EC
 ...(ii)
...(ii)समीकरण (i) और (ii) की तुलना करने पर, हमें प्राप्त होता है
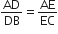
DE||BC
ABCD एक समलंब है जिसमें AB||DC है तथा इसके विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। दर्शाइए कि  है।
है।
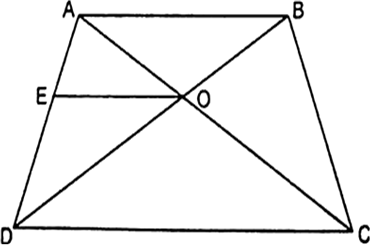

रचना: EO||DC||AB बनाइए
∆ADC में,
EO||DC
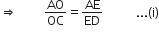
∆ADB में,
EO||DC
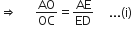
EO||AB
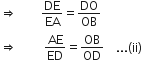
समीकरण (i) और (ii) की तुलना करने पर, हमें प्राप्त होता है

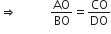
एक चतुर्भुज ABCD के विकर्ण परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि  है। दर्शाइए कि ABCD एक समलंब है।
है। दर्शाइए कि ABCD एक समलंब है।
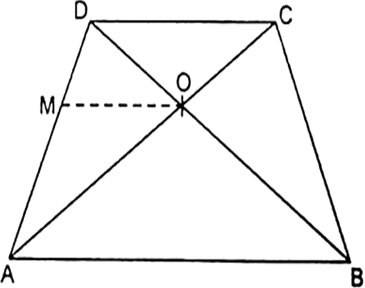
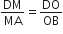
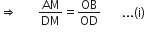
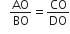
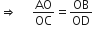 ...(ii)
...(ii)समीकरण (i) और (ii) की तुलना करने पर, हमें प्राप्त होता है
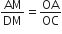
OM||DC
OM||AB
⇒ AB||DC
अत: ABCD एक समलंब है।
बताइए कि आकृति में दिए त्रिभुजों के युग्मों में से कौन-कौन से युग्म समरूप हैं। उस समरूपता कसौटी को लिखिए जिसका प्रयोग आपने उत्तर देने में किया है तथा साथ ही समरूप त्रिभुजों को सांकेतिक रूप में व्यक्त कीजिए।
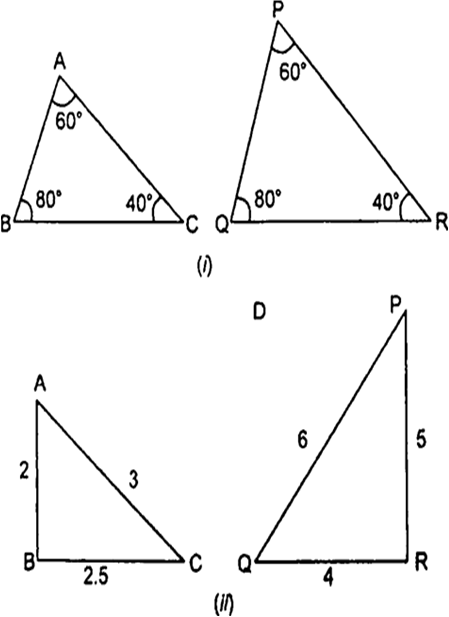
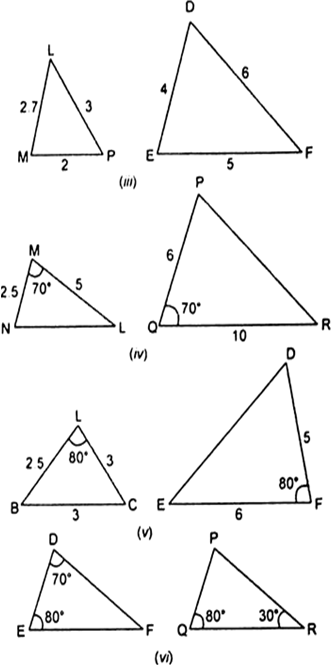
(i) ∆ABC और ∆PQR में,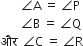
∆ABC ~ ∆PQR
(ii) ∆ABC और ∆QRP में,
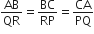
∴ 
(iii) समरूप नहीं है।
(iv) ∆MNL और ∆QPR में,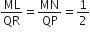
और 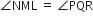
∴ ∆MNL ~ ∆QPR
समरूप नहीं है।
(v) समरूप नहीं है।
(vi) ∆DEF और ∆PQR में,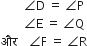
∴ ∆DEF ~ ∆PQR
Sponsor Area
आकृति में ∆ODC~∆OBA, 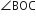 = 125° और
= 125° और  = 70° है।
= 70° है।  ज्ञात कीजिए।
ज्ञात कीजिए।
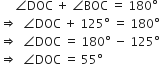
∆DOC में,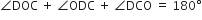
[त्रिभुज के तीनों कोणों का योग]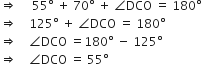
∵ ∆ODC ~ ∆OBA [ दिया है ]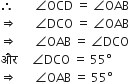
आकृति में, 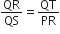 तथा
तथा  है। दर्शाइए कि ∆PQS ~ ∆TQR है।
है। दर्शाइए कि ∆PQS ~ ∆TQR है।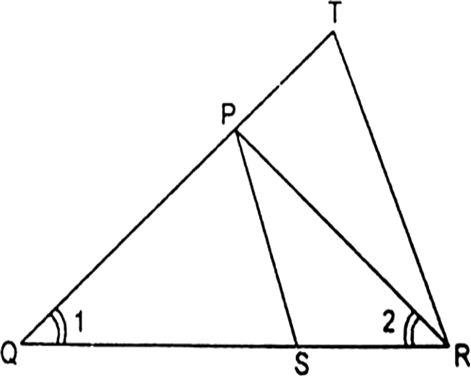
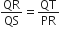
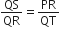 ...(i)
...(i) [ दिया है ]
[ दिया है ]⇒ PR = PQ ...(ii)
अब, ∆PQS और ∆TQR में,
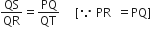
और
 [ उभयनिष्ट ]
[ उभयनिष्ट ]∆PQS ~ ∆TQR
∆PQR की भुजाओ PR और QR पर क्रमश: बिंदु S और T इस प्रकार स्थित है की 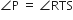 है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
है। दर्शाइए कि ∆RPQ ~ ∆RTS है।
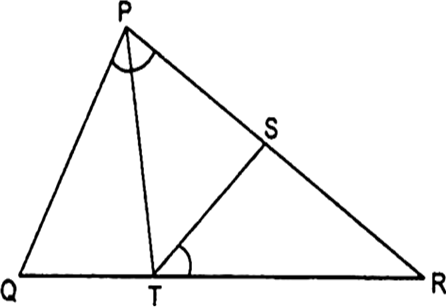
∆RPQ और ∆RTS में,
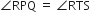 [ दिया है ]
[ दिया है ]
और  [ उभयनिष्ट ]
[ उभयनिष्ट ]
∆RPQ ~ ∆RTS
आकृति में,  के शीर्षलंब AD और CE परस्पर बिंदु P पर पटिच्छेद करते हैं। दर्शाइए कि:
के शीर्षलंब AD और CE परस्पर बिंदु P पर पटिच्छेद करते हैं। दर्शाइए कि:
(i) ∆AEP ~ ∆CDP
(ii) ∆ABD ~ ∆CBE
(iii) ∆AEP ~ ∆ADB
(iv) ∆PDC ~ ∆BEC
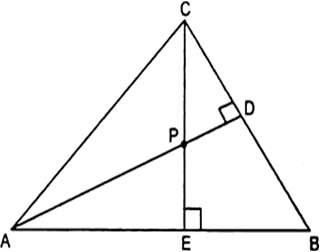
AD और CD की भुजाएँ एक दूसरे को P पर प्रतिच्छेद करती हैं।
(i) ∆AEP और ∆CDP में, [ दिया है ]
[ दिया है ]
और 
∆AEP ~ ∆CDP
(ii) ∆ABD और ∆CBE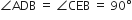 [ दिया है ]
[ दिया है ]
और  [ उभयनिष्ट ]
[ उभयनिष्ट ]
∆ABD ~ ∆CBE
(iii) ∆AEP और ∆ADB [ दिया है ]
[ दिया है ]
और  [ उभयनिष्ट ]
[ उभयनिष्ट ]
∆AEP ~ ∆ADB
(iv) ∆PDC और ∆BEC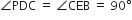 [ दिया है ]
[ दिया है ]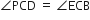 [ उभयनिष्ट ]
[ उभयनिष्ट ]
∆PDC ~ ∆BEC
समांतर चतुर्भुज ABCD की बढ़ाई गई भुजा AD पर स्थित E एक बिंदु है तथा BE भुजा CD को F पर प्रतिच्छेद करती है। दर्शाइए कि ∆ABE ~ ∆CFB है।
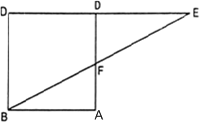
∆ABE और ∆CFB में,
 [ एकान्तर कोण ]
[ एकान्तर कोण ]और
 [ सम्मुख कोण ]
[ सम्मुख कोण ]∆ABE ~ ∆CFB
आकृति में, ABC और AMP दो समकोण त्रिभुज हैं, जिनके कोण B और M समकोण हैं। सिद्ध कीजिए कि:
(i) 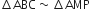
(ii) 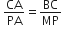

दिया है: ∆ABC और ∆AMP समकोण त्रिभुज हैं।
(i) ∆ABC और ∆AMP में,
 [ दिया है ]
[ दिया है ]
और  [ उभयनिष्ट ]
[ उभयनिष्ट ]
∆ABC ~ ∆AMP
(ii)
∵ ∆ABC ~ ∆AMP
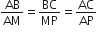

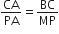
CD और GH क्रमश:  के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमश: ΔABC और ΔFEG कि भुजाओं AB और FE पर स्थित हैं। यदि ΔABC~ΔFEG है, तो दर्शाइए कि:
के ऐसे समद्विभाजक हैं कि बिंदु D और H क्रमश: ΔABC और ΔFEG कि भुजाओं AB और FE पर स्थित हैं। यदि ΔABC~ΔFEG है, तो दर्शाइए कि:
(i) 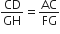
(ii) 
(iii) 
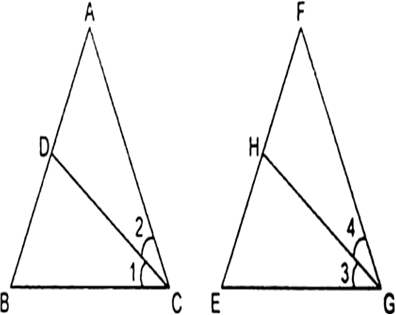
(i)
 ...(i)
...(i)

और


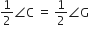

 ...(ii)
...(ii)ΔACD और ΔFGH में,

∆ACD ~ ∆FGH अथवा ∆DCA ~ ∆HGF
(ii)


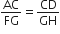
(iii) ∆DCB और ∆HGE में,

[∵ ∆ABC ~ ∆FEG]
∆DCB ~ ∆HGF
आकृति में, AB=AC वाले, एक समद्विबाहु त्रिभुज ABC कि बढ़ाई गई भुजा CB पर स्थित E एक बिंदु है। यदि  है तो सिद्ध कीजिए कि ΔABD~ΔECF है।
है तो सिद्ध कीजिए कि ΔABD~ΔECF है।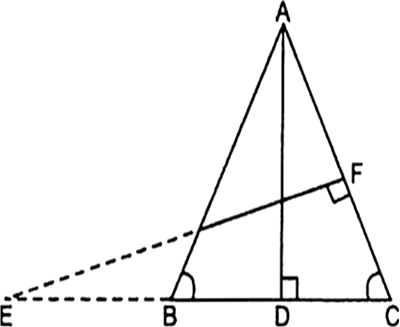
∆ABD और ∆ECF में,
∆ABD = ∆ECF 
और 
∆ABD ~ ∆ECF
एक त्रिभुज ABC की भुजाएँ AB और BC तथा मध्यिका AD एक अन्य त्रिभुज PQR की क्रमश: भुजाओं PQ और QR तथा मध्यिका PM के समानुपाती हैं। दर्शाइए कि ∆ABC~∆PQR है।
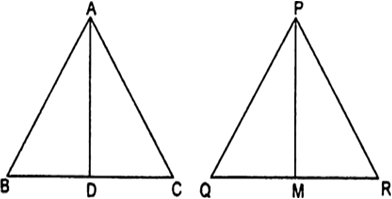


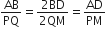


∆ABD~∆PQM
⇒ ∠B = ∠Q
∆ABC और ∆PQR में,
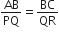
और

∆ABC~∆PQR
एक त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि  है। दर्शाइए कि CA2=CB.CD है।
है। दर्शाइए कि CA2=CB.CD है।
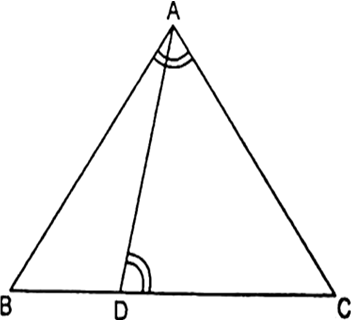
∆DAC और ∆ABC में,
 [दिया है]
[दिया है] [उभयनिष्ट]
[उभयनिष्ट]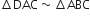

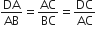

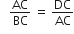


एक त्रिभुज ABC की भुजाएँ AB और AC तथा मध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा मध्यिका PM के क्रमश: समानुपाती हैं।दर्शाइए कि ∆ABC~∆PQR है।
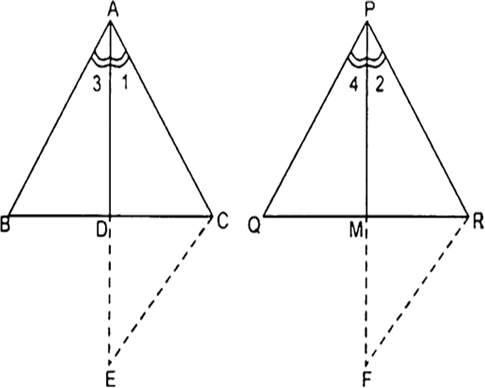
∆ABD और ∆CDE में,
AD = DE
और BD = DC [AD समद्विभाजक है]



इसी तरह, 


दिया है कि,

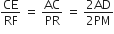
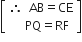




 ...(i)
...(i)
इसी प्रकार,
 ...(ii)
...(ii)
समीकरण (i) और (ii) को जोड़ने पर

∆ABC और ∆PQR में,
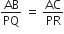
और 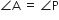
अत: सिद्ध होता है कि ∆ABC ~ ∆PQR
लंबाई 6 m वाले एक ऊर्ध्वाधर स्तंभ की भूमि पर छाया की लंबाई 4 m यही, जबकि उसी समय एक मीनार की छाया की लंबाई 28 m है। मीनार की ऊँचाई ज्ञात कीजिए।
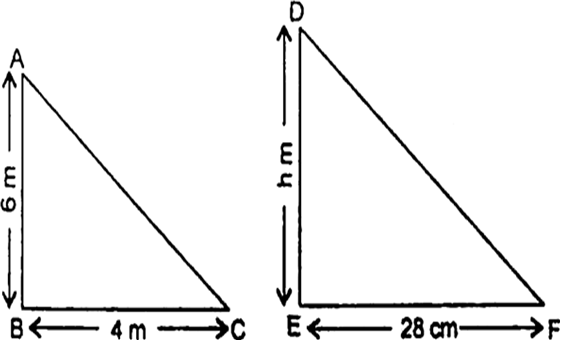

Δ ABC तथा ΔPQR में,
 (प्रत्येक 90o)
(प्रत्येक 90o) (सूर्य का उन्नयन कोण समान है)
(सूर्य का उन्नयन कोण समान है) ΔABC ~ ΔPQR
ΔABC ~ ΔPQR
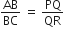

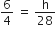

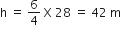
AD और PM त्रिभुजों ABC और PQR की क्रमश: मध्यिकाएँ हैं, जबकि ∆ABC ~ ∆PQR है। सिद्ध कीजिए कि 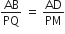 है।
है।
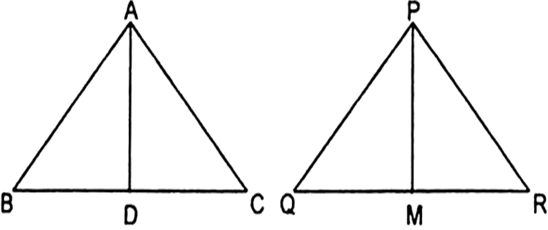 .
.दिए है,


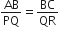

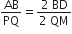

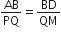 [∵ AD और PM माध्यिकाएँ हैं]
[∵ AD और PM माध्यिकाएँ हैं]∆ABD और ∆PQM में, हमें प्राप्त होता है
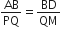
और
 [∵ ∆ABC ~ ∆PQR]
[∵ ∆ABC ~ ∆PQR]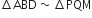

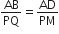
मान लीजिए ∆ABC~∆DEF है और इनके क्षेत्रफल क्रमश: 64cm2 और 121cm2 हैं। यदि EF=15.4cm2 हो, तो BC ज्ञात कीजिए।


अत: 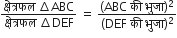
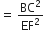

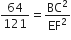

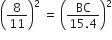

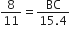

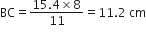
अत:, BC = 11.2 cm
एक समलंब ABCD जिसमें AB||DC है, के विकर्ण परस्पर बिंदु O पर प्रतिच्छेद करते हैं। यदि AB = 2CD हो तो त्रिभुजों AOB और COD के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
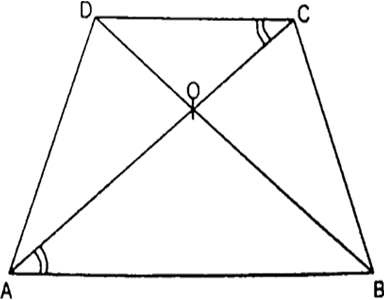
∆AOB और ∆COD में,
 [एकांतर कोण]
[एकांतर कोण]और
 [सम्मुख कोण]
[सम्मुख कोण]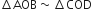

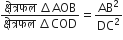
परन्तु AB = 2DC
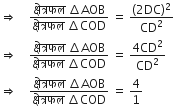
आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि 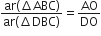 है।
है।
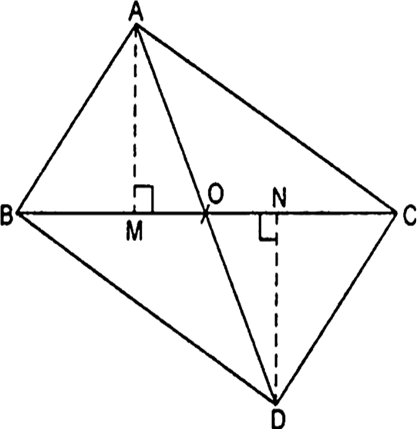
A तथा D से BC पर लंब AM और DN खींचो।
∆AMO और ∆DNO में,

[शीर्षाभिमुख कोण]
∆AMO ~ ∆DNO
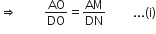
अब,
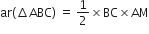
और
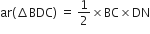
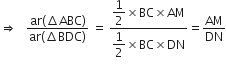
परन्तु

अत: यह सिद्ध होता है कि

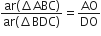
यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।
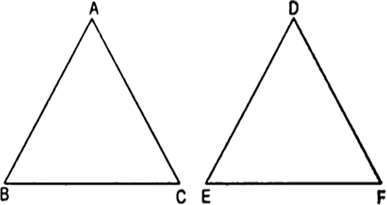


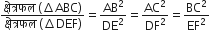
परन्तु


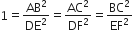



और




और

∆ABC और ∆DEF में,
AB = DE
AC = DF
और BC = EF

एक त्रिभुज ABC की भुजाओं AB, BC और CA के मध्य-बिंदु क्रमश: D, E और F हैं। ∆DEF और ∆ABC के क्षेत्रफलों का अनुपात ज्ञात कीजिए।
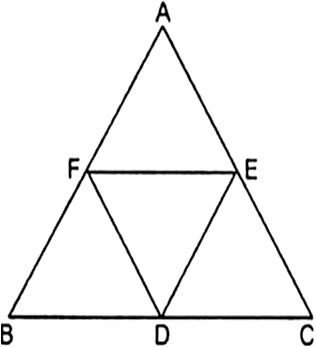
D, E तथा F; BC, AC तथा AB के मध्य बिंदु हैं, अत: DE||AB या EF||BC तथा FD||AC
ज्ञात करना है =

और
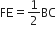


और
 [BDEF एक समचतुर्भुज है]
[BDEF एक समचतुर्भुज है]इसी प्रकार ∆DEF और ∆ABC में,
 [समचतुर्भुज के विपरीत कोण]
[समचतुर्भुज के विपरीत कोण]और



अत:,
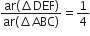
सिद्ध कीजिए कि दो समरूप त्रिभुजों के क्षेत्रफलों का अनुपात इनकी संगत माध्यिकाओं के अनुपात का वर्ग होता है।
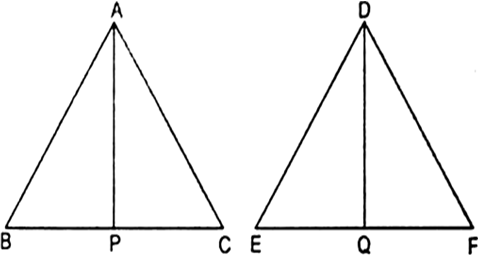
∵


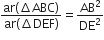 ...(i)
...(i)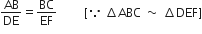

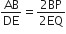



और

Therefore, by using SAS similar condition
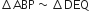
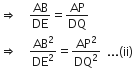
समीकरण (i) और (ii) की तुलना करने पर
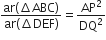
सिद्ध कीजिए कि एक वर्ग की किसी भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल उसी वर्ग के एक विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
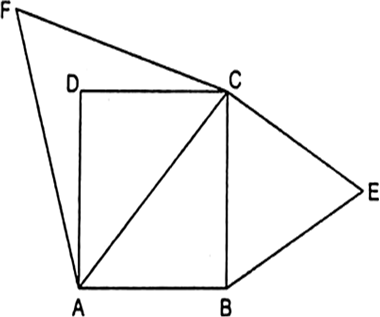
∵ ∆BCE और ∆ACF समबाहु त्रिभुज हैं।

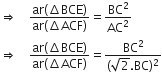
[वर्ग के विकर्ण =
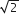 x भुजा]
x भुजा]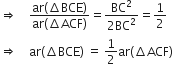
Sponsor Area
ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बंदु है। त्रिभुजों ABC और BDE के क्षेत्रफलों का अनुपात है:
-
2:1
-
1:2
-
4:1
-
1:4
2:1
1:2
4:1
1:4
∆ABC और ∆BDE दोनों समबाहु त्रिभुज हैं।
∴ ∆ABC ~ ∆BDE
∴ 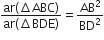

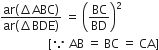
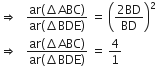
अत: C(4:1) सही उत्तर है
दो समरूप त्रिभुजों कि भुजाएँ के अनुपात में हैं। इन त्रिभुजों के क्षेत्रफलों का अनुपात है:
-
2:3
-
4:9
-
81:16
-
16:81
त्रिभुजों के क्षेत्रफलों का अनुपात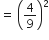
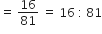
कुछ त्रिभुजों की भुजाएँ नीचे दी गई हैं। नर्धारित कीजिए कि इनमें से कौन-कौन से त्रिभुज समकोण त्रिभुज हैं। इस स्थिति में कर्ण की लंबाई भी लिखिए।
(i) 7 cm, 24 cm, 25 cm (ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm (iv) 13 cm, 12 cm, 5 cm
(i) 7 cm, 24 cm, 25 cm
72 = 49
242 = 576
और 252 = 625
हम देखते हैं कि
72 + 242 = 252
∴ दी गई त्रिभुज एक समकोण त्रिभुज है।
विकर्ण कि लंबाई = 25 cm
(ii) 3 cm, 8 cm, 6 cm
32 = 9
82 = 64
62 = 36
∵ 32 + 62 ≠ 82
∴ दी गई त्रिभुज एक समकोण त्रिभुज नहीं है।
(iii) 50 cm, 80 cm, 100 cm
502 = 2500
802 = 6400
1002 = 10000
∵ 502 + 802 ≠ 1002
∴ दी गई त्रिभुज एक समकोण त्रिभुज नहीं है।
(iv) 13 cm, 12 cm, 5 cm
132 = 169
122 = 144
52 = 25
∵ 52 + 122 ≠ 132
∴ दी गई त्रिभुज एक समकोण त्रिभुज है।
विकर्ण कि लंबाई = 13 cm
PQR एक समकोण त्रिभुज है जिसका कोण P समकोण है तथा QR पर बिंदु M इस प्रकार स्थित है कि PM⊥QR है। दर्शाइए कि PM2 = QM.MR है।
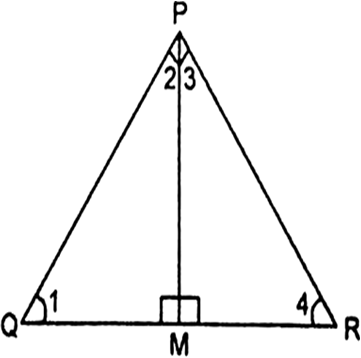
ΔPQR में,
∵
 [दिया है]
[दिया है]⇒
 ...(i)
...(i)∵
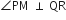
इसलिए,
 ...(ii)
...(ii)समीकरण (i) और (ii) की तुलना करने पर

इस प्रकार,

∆PRM और ∆QPM में,

और

इसलिए,


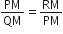


आकृत में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा  है। दर्शाइए कि
है। दर्शाइए कि
(i) AB2 = BC.BD
(ii) AC2 = BC.DC
(iii) AD2 = BD.CD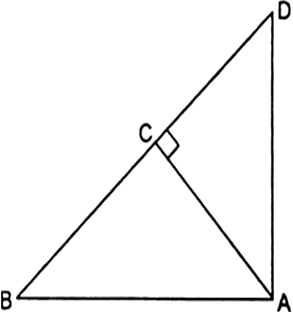
(i) ∆BAC और ∆BDA में,
 ...(i)
...(i)
समकोण ∆ABC में,
 ...(ii)
...(ii)
समकोण ∆ABD में,
 ...(iii)
...(iii)
समीकरण और की तुलना करने पर

और,  [दोनों कोण 90o हैं]
[दोनों कोण 90o हैं]
∴ ∆BAC ~ ∆BDA
∴ 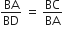
⇒ BA2 = BC.BD
⇒ AB2 = BC.BD
(ii) समकोण ∆ACB और ∆DCA में,


∴ ∆ACB ~ ∆DCA
∴ 
⇒ AC2 = BC.DC
(iii) समकोण ∆ADB और ∆CDA में,

 (उभयनिष्ट)
(उभयनिष्ट)
∴ ∆ADB ~ ∆CDA
∴ 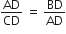
⇒ AD2 = BD.CD
ABC एक समद्विबाहु त्रिभुज है जिसका कोण C समकोण है। सिद्ध कीजिए कि AB2=2AC2 है।
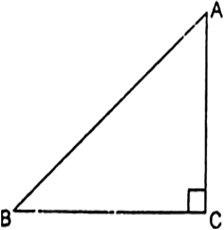
∴ AB2 = AC2 + BC2
⇒ AB2 = AC2 + AC2
[∵ BC = AC]
⇒ AB2 = 2 AC2
ABC एक समद्विबाहु त्रिभुज है जिसमें AC=BC है। यदि AB2=2AC2 है, तो सिद्ध कीजिए कि ABC एक समकोण त्रिभुज है।
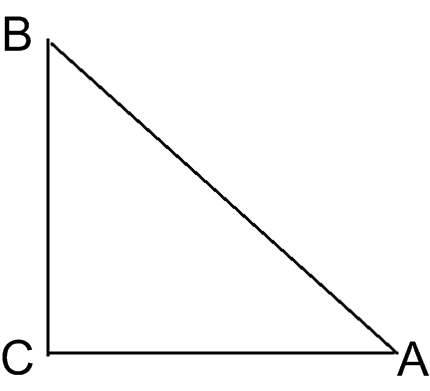
⇒ AB2 = AC2 + AC2
⇒ AB2 = AC2 + BC2
[∵ AC = BC]
⇒ ∆ABC एक समकोण त्रिभुज है और और कोण C समकोण है।
एक समबाहु त्रिभुज ABC की भुजा 2a है। उसके प्रत्येक शीर्षलंब की लंबाई ज्ञात कीजिए।
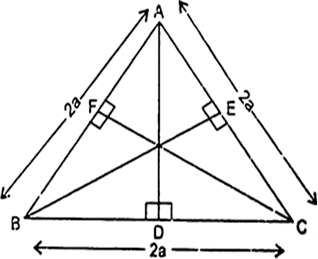
समकोण ΔADB और ΔADC में,
विकर्ण AB = विकर्ण AC [दिया है]
AD = AD [उभयनिष्ट भुजा]

∴ BD = CD
=
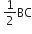
[∵ जहाँ BC का मध्य बिंदु D है]

समकोण ΔADB में,
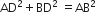
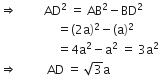
इस प्रकार,

और

सिद्ध कीजिए कि एक समचतुर्भुज की भुजाओं के वर्गों का योग विकर्णों के वर्गों के योग के बराबर होता है।
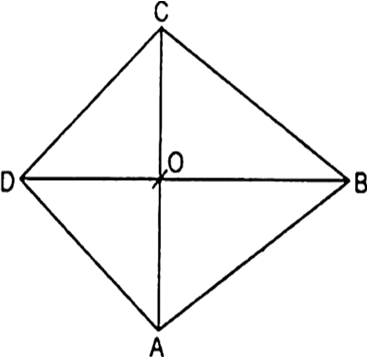
माना ABCD एक समचतुर्भुज है जिसके विकर्ण AC तथा BD एक-दूसरे को O पर प्रतिच्छेद करते हैं।
हम जानते हैं कि समचतुर्भुज की भुजाएँ बराबर होती हैं तथा विकर्ण एक-दूसरे पर लंबवत होते हैं तथा एक-दूसरे को समद्विभाजित करते हैं।
समकोण ∆AOB में,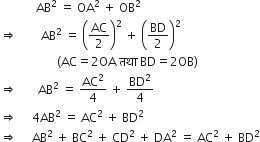
आकृति में ΔABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD⊥BC, OE⊥AC और OF⊥AB है। दर्शाइए कि
(i) OA2 + OB2 + OC2 - OD2 - OE2 - OF2 = AF2 + BD2 + CE2,
(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2
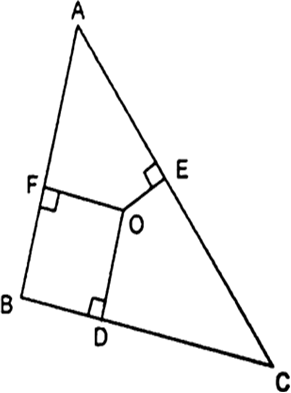
(i) समकोण ΔOFA में,
OA2 = AF2 + OF2 ...(i)
समकोण ΔOBD में,
OB2 = OD2 + BD2 ...(ii)
समकोण ΔOEC में,
OC2 = OE2 + CE2 ...(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर, हमें प्राप्त होता है:
OA2 + OB2 + OC2 = AF2 + OF2 + OD2 + BD2 + OE2 + CE2
⇒ OA2 + OB2 + OC2 = AF2 + BD2 + CE2 + OD2 + OF2 + OE2
⇒ AF2 + BD2 + CE2 = OA2 + OB2 + OC2 - OD2 - OF2 - OE2
(ii) AF2 + BD2 + CE2 = (OA2 - OE2) + (OB2 - OF2) + (OC2 - OD2)
= AE2 + CD2 + BF2
अत:, AF2 + BD2 + CE2 = AE2 + CD2 + BF2
10m लंबी एक सीढ़ी एक दीवार पर टिकाने पर भूमि से 8m की ऊँचाई पर स्थित एक खिड़की तक पहुँचती है। दीवार के आधार से सीढ़ी के निचले सिरे की दूरी ज्ञात कीजिए।
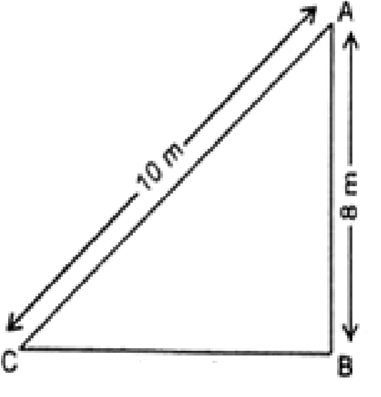
माना सीढ़ी है तथा A खिड़की है। AC = 10 m
समकोण ΔABC में,,
AC2 = AB2 + BC2
⇒ BC2 = AC2 - AB2
= BC2 = (10)2 - (8)2
= BC2 = 100 - 64 = 36
⇒ BC = 6 m
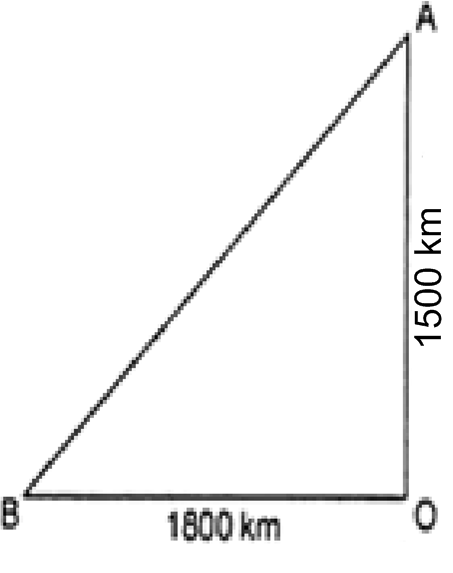
एक हवाई जहाज एक हवाई अड्डे से उत्तर की ओर 1000 km/h की चाल से उड़ता है। इसी समय एक अन्य जाहज उसी हवाई अड्डे से पश्चिम की ओर 1200 km/h की चाल से उड़ता है। 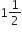 घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
घंटे के बाद दोनों हवाई जहाजों के बीच की दूरी कितनी होगी?
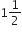 घंटे बाद उत्तर दिशा में चली दूरी
घंटे बाद उत्तर दिशा में चली दूरी 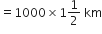
=
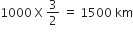
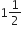 घंटे बाद पश्चिम दिशा में चली दूरी =
घंटे बाद पश्चिम दिशा में चली दूरी = 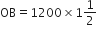
=
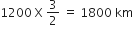
समकोण ΔAOB में,




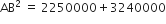

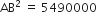



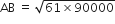


दो खंभे जिनकी ऊँचाईयाँ 6m और 11m हैं तथा ये समतल भूमि पर खड़े हैं। यदि इनके ऊपरी सिरों के बीच की दूरी 12m है तो इनके ऊपरी सिरों के बीच की दूरी ज्ञात कीजिए।

DC⊥BE खींचो, DE को मिलाओ
ABCD एक आयत है और BC और AD विपरीत भुजाएँ हैं।
∴ BC = AD
[∵ आयत की विपरीत भुजाएँ समान होती हैं] = 6 m
इस प्रकार, DC = AB = 12 cm
अब, CE = BE - BC
= 11 m - 6 m = 5 m
दुबारा, समकोण ΔDCE में,
DE2 = DC2 + CE2
= (12)2 + (5)2
= 144 + 25 = 169

एक त्रिभुज ABC जिसका कोण C समकोण है, की भुजाओं CA और CB पर क्रमश: बिंदु D और E स्थित हैं। सिद्ध कीजिए कि AE2 + BD2 = AB2 + DE2 है।
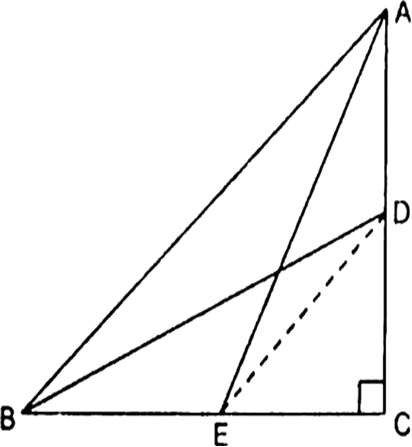
∆ACE में,
AE2 = AC2 + CE2 ...(i)
∆BCD में,
BD2 = CD2 + BC2 ...(ii)
समीकरण (i) और (ii) को जोड़ने पर
AE2 + BD2 = (AC2 + BC2) + (CE2 + CD2)
⇒ AE2 + BD2 = AB2 + DE2
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है। सिद्ध कीजिए कि 2AB2=2AC2+BC2 है।
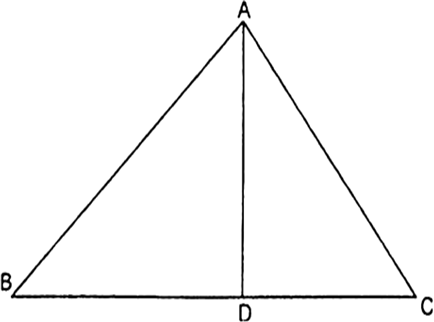
∵ DB = 3CD [दिया है]
अब, BC = CD + DB BC = CD+ 3CD
BC = CD+ 3CD BC = 4CD
BC = 4CD
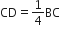
समकोण ΔADB में,
AB2 = AD2 + DB2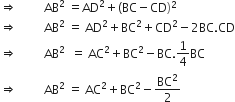
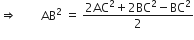

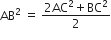

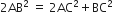
किसी समबाहु त्रिभुज ABC कि भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि  है। सिद्ध कीजिए कि 9AD2=7AB2 है।
है। सिद्ध कीजिए कि 9AD2=7AB2 है।
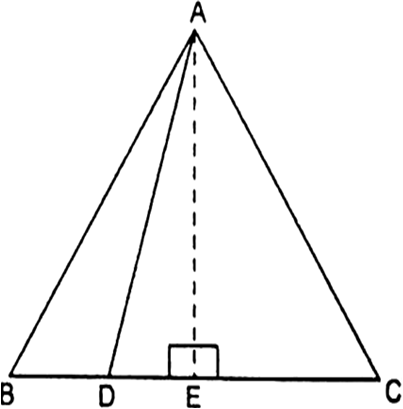
AE = AE [उभयनिष्ट]

और AB = AC

 BE = CE
BE = CE
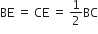
समकोण ΔADE में


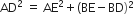





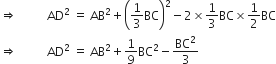




और AB = BC = CA




किसी समबाहु त्रिभुज में, सिद्ध कीजिए कि उसकी एक भुजा के वर्ग का तिगुना उसके एक शीर्षलंब के वर्ग के चार गुने के बराबर होता है।
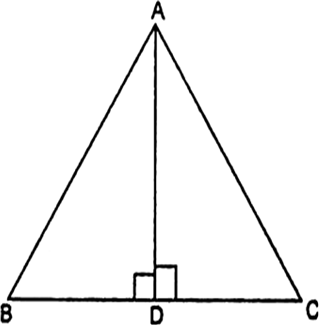
AB = AC [समबाहु ∆ है]
 [उभयनिष्ट]
[उभयनिष्ट]और


 BD = DC
BD = DC
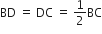
समकोण ∆ABD में,


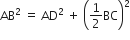

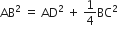

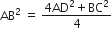

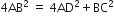

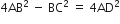

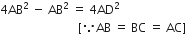


सही उत्तर चुनकर उसका औचित्य दीजिए: ∆ABC में  और BC=6cm है। कोण B है:
और BC=6cm है। कोण B है:
-
120o
-
60o
-
90o
-
45o
120o
60o
90o
45o
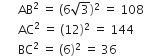
अब, 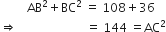
∴ ∆ABC B पर एक समकोण त्रिभुज है।
अत: सही उत्तर (c) = 90o है।
आकृति में PS कोण QPR का समद्विभाजक है। सिद्ध कीजिए कि 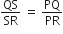 है।
है।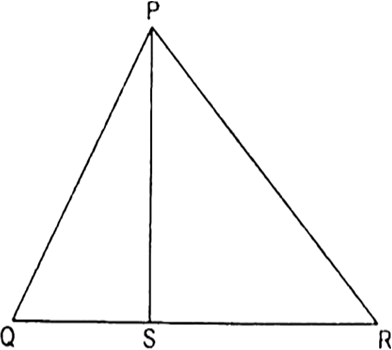
∴
 [एकांतर कोण]
[एकांतर कोण]
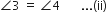 [सम्मुख कोण]
[सम्मुख कोण]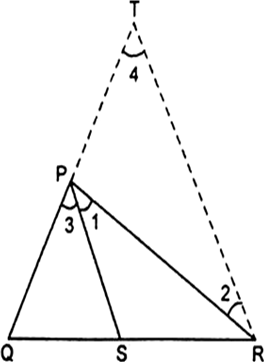
परन्तु  [दिया है]
[दिया है]
∴  [समीकरण (i) और (ii) से]
[समीकरण (i) और (ii) से]
∴ PT = PR ...(iii)
अब ∆ORT में,
PS = RT
∴ 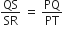

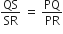
आकृति में D त्रिभुज ABC के कर्ण AC पर स्थित एक बिंदु है जबकि BD⊥AC तथा DM⊥BC और DN⊥AB है। सिद्ध कीजिए कि
(i) DM2 = DN.MC
(ii) DN2 = DM.AN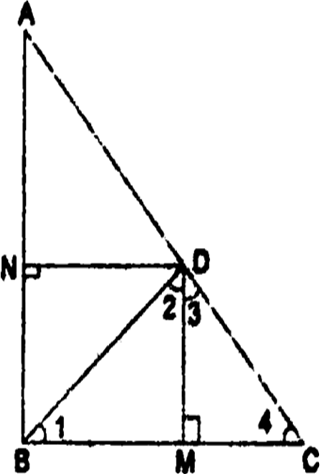
(i) ∆CDM~∆DBM 
(ii) ∆ADN~∆DBN 

आकृति में ABC एक त्रिभुज है जिसमें है  तथा AD⊥CB है। सिद्ध कीजिए कि AC2=AB2+BC2+2BC.BD है।
तथा AD⊥CB है। सिद्ध कीजिए कि AC2=AB2+BC2+2BC.BD है।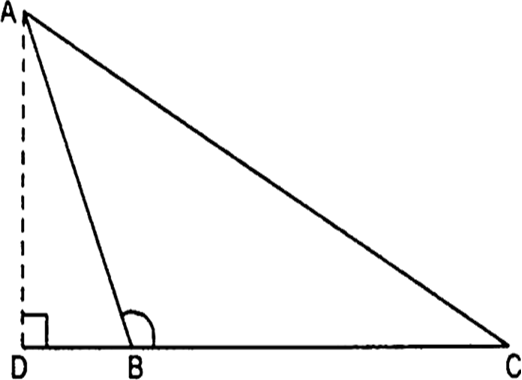
समकोण ΔADB में,
AB2 = AD2 + BD2 ...(i)
समकोण ∆ADC में,
AC2 = AD2 + DC2
⇒ AC2 = AD2 + (BD + BC)2
⇒ AC2 = AD2 + BD2 + BC2 + 2BD.BC
⇒ AC2 = AB2 + BC2 + 2BC.BD [समीकरण (i) से]
आकृति में ABC एक त्रिभुज है जिसमें  है तथा AD⊥BC है। सिद्ध कीजिए कि AC2=AB2+BC2-2BC.BD है।
है तथा AD⊥BC है। सिद्ध कीजिए कि AC2=AB2+BC2-2BC.BD है।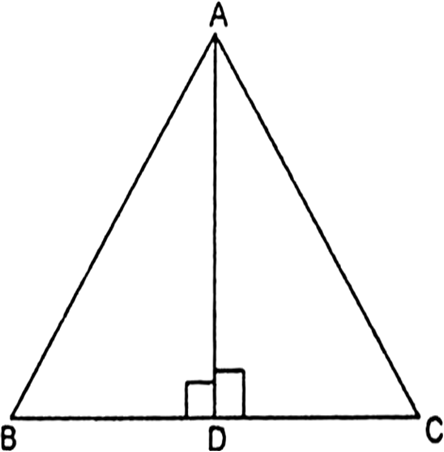
समकोण ∆ABD में,
AB2 = AD2 + BD2 ...(i)
समकोण ∆ADC में,
AC2 = AD2 + DC2
⇒ AC2 = AD2 + (BC - BD)2
⇒ AC2 = AD2 + BC2 - 2BC.BD + BD2
⇒ AC2 = (AD2 + BD2) + BC2 - 2BC.BD
⇒ AC2 = AB2 + BC2 - 2BC.BD [समीकरण (i) से]
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM⊥BC है। सिद्ध कीजिए कि
(i) 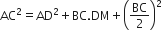
(ii) 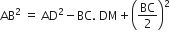
(iii) 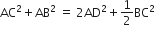

AC2 = AM2 + MC2
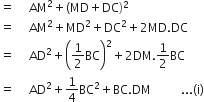
(ii) समकोण ΔABM में,
AB2 = AM2 + BM2
= AM2 + (BD - MD)2
= AM2 + BD2 + MD2 - 2BD.MD
= (AM2 + MD2) + BD2 - 2BD.MD
=

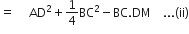
(iii) समीकरण (i) और (ii) को जोड़ने पर
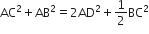
सिद्ध कीजिए कि एक समांतर चतुर्भुज के विकर्णों के वर्गों का योग उसकी भुजाओं के वर्गों के योग के बराबर होता है।
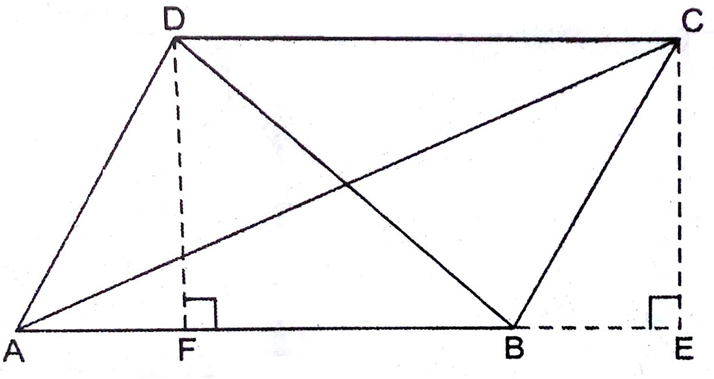
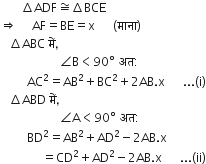
समीकरण (i) और (ii) से,
AC2+BD2=AB2+BC2+CD2+AD2
आकृति में एक वृत्त की दो जिवाएँ AB और CD परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆APC~∆DPB
(ii) AP.PB=CP.DP
 (शीर्षाभिमुख कोण)
(शीर्षाभिमुख कोण) (एक ही वृत्तखंड के कोण)
(एक ही वृत्तखंड के कोण)∴ ∆APC ~ ∆DPB
(ii) अत:
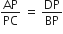 (संगत भुजाओं का अनुपात)
(संगत भुजाओं का अनुपात)
आकृति में एक वृत्त की दो जिवाएँ AB और CD बढ़ाने पर परस्पर बिंदु P पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि
(i) ∆PAC~∆PDB (ii) PA.PB=PC.PD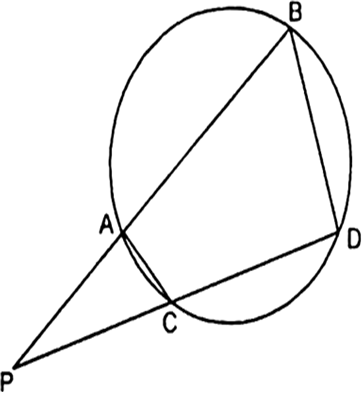
(i)  ...(i)
...(i)
और  ...(ii)
...(ii)
समीकरण (i) और (ii) से
∆PAC ~ ∆PDB
(ii) ∆PAC ~ ∆PDB [ऊपर सिद्ध किया है]
∴ 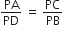 [∵ समरूप त्रिभुजों की संगत भुजाओं का अनुपात]
[∵ समरूप त्रिभुजों की संगत भुजाओं का अनुपात]
⇒ PA.PB ~ PC.PD
आकृति में त्रिभुज ABC की भुजा BC पर एक बिंदु D इस प्रकार स्थित है कि 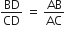 है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।
है। सिद्ध कीजिए कि AD, कोण BAC का समद्विभाजक है।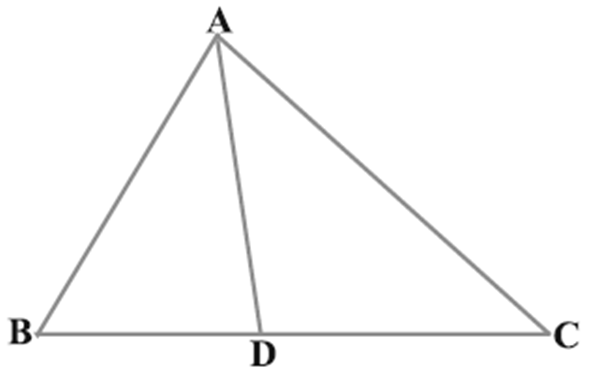
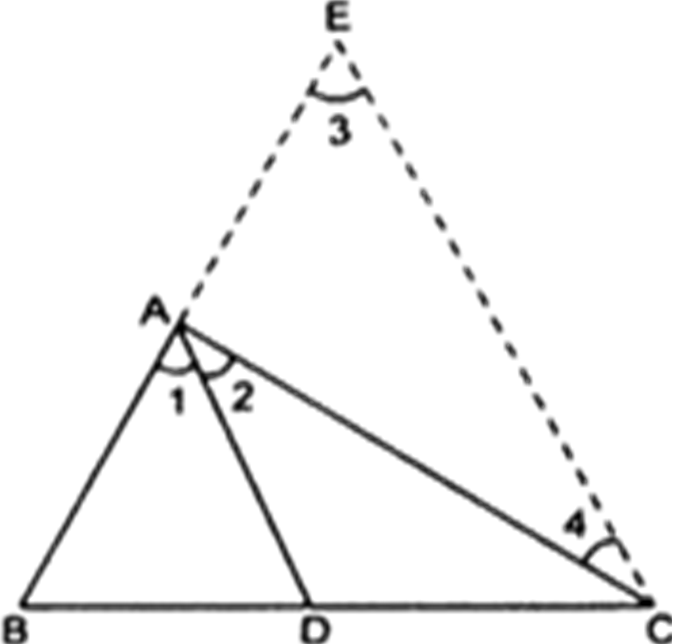
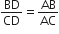 [दिया है]
[दिया है]
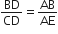
[∵ AC = AE]
∴ ∆BCE में,
AD||CE
 ...(i)
...(i)और
 ...(ii)
...(ii)∵ AC = AE
∴ ...(iii)
...(iii)अर्थात 
अत: 
अत: AD, कोण BAC का समद्विभाजक है।
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकली हुई है? यदि वह डोरी को 5cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाज़िमा की काँटे से क्षैतिज दूरी कितनी होगी?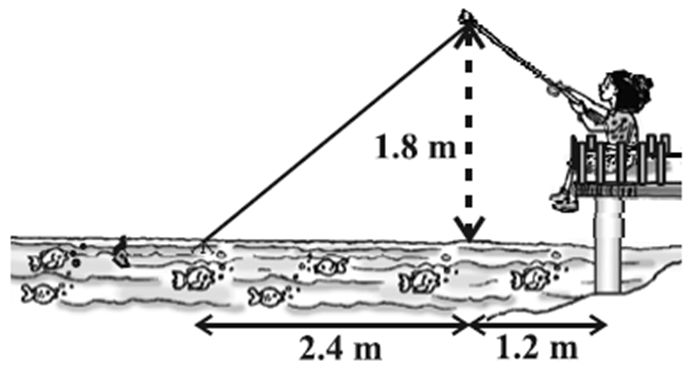
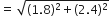
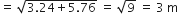
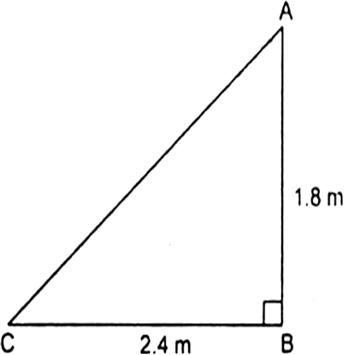
अत: जो डोरी बाहर है उसकी लंबाई = 3m
अब,
12 सेकंड में 5cm/s की दर से खींची गई डोरी की लंबाई
= 5×12 = 60cm = 0.6cm
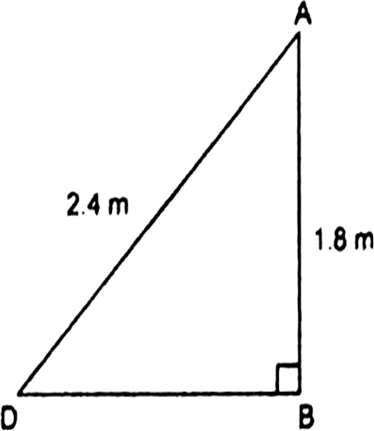
∴ शेष बची डोरी की लंबाई
= 3.0 - 0.6 = 2.4 m
अब,

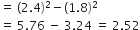

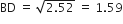 (लगभग)
(लगभग)अत: 12 सेकंड बाद नाज़िमा की काँटे क्षैतिज दूरी = (1.59 + 1.2)m
= 2.79 m (लगभग)
आकृति 2 में, एक ABC के अंतर्गत एक वृत्त बना है जो त्रिभुज की भुजाओं AB, BC तथा CA को क्रमशः बिंदुओं D, E तथा F पर स्पर्श करता है। यदि AB, BC तथा CA की लंबाइयाँ क्रमशः 12 सेमी, 8 सेमी तथा 10 सेमी हैं, तो AD, BE तथा CF की लंबाइयाँ ज्ञात कीजिए।
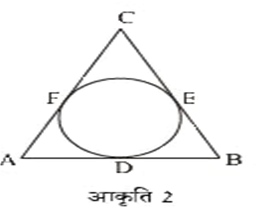
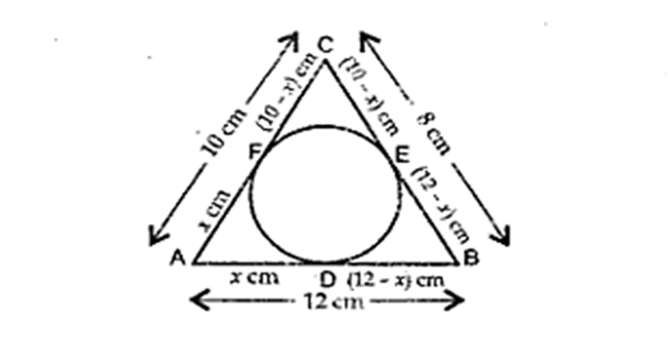
जैसा कि हम जानते हैं,
AF = AD, CF = CE, BD = BE
माना AD =AF = x cm,
तब, DB = AB - AD = (12 - x) cm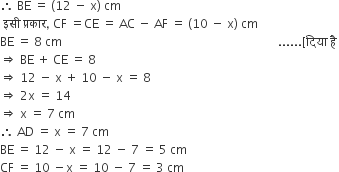
दर्शाइए कि  जहॉं
जहॉं  तथा
तथा  जहॉं
जहॉं  है, समरूप त्रिभुज हैं।
है, समरूप त्रिभुज हैं।
ABC में, ऊर्ध्वाधर के निर्देशांक A(-2, 0), B(2, 0), C(0, 2) हैं।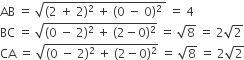
Δ PQR में, ऊर्ध्वाधर के निर्देशांक P(-4, 0), Q(4, 0), R(0, 4) हैं।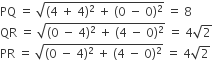
अब, ABC और ΔPQR के समान होने के लिए, संबंधित पक्ष आनुपातिक होना चाहिए।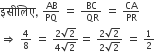
इस प्रकार, Δ ABC, ΔPQR के समान है।
सिद्ध कीजिए कि किसी वर्ग की एक भुजा पर बनाए गए समबाहु त्रिभुज का क्षेत्रफल, इसके विकर्ण पर बनाए गए समबाहु त्रिभुज के क्षेत्रफल का आधा होता है।
दिया गया: ABCD वर्ग, विकर्ण BD △ BCE जिसे आधार BC △ BDF पर वर्णित किया गया है जिसे आधार BD दोनों में वर्णित किया गया है △ BCE और △ BDF समतुल्य
सिद्ध करना:
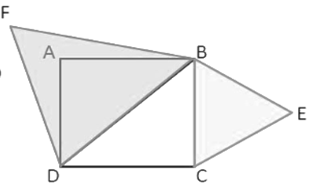
प्रमाण:
△ BCE और △ BDF दोनों समकक्ष
△ BCE और △ BDF में
(SSS समानता से)
△ FBD ~ △ BCE
हम जानते हैं कि समान त्रिकोणों में, त्रिकोण के क्षेत्र का अनुपात संबंधित पक्षों के वर्ग के अनुपात के बराबर है
DB ( ) वर्ग ABCD का विकर्ण है अत,
यदि दो समरूप त्रिभुजों के क्षेत्रफल समान हों, तो सिद्ध कीजिए कि वह त्रिभुजें सर्वांगसम होती हैं।
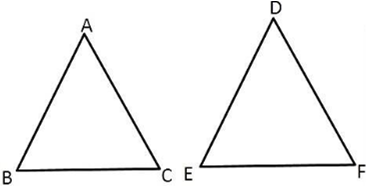
माना ΔABC और ΔDEF दोनों त्रिभुज समरूप है,
ΔABC ~ ΔDEF
माना ΔABC और ΔDEF दोनों त्रिभुज का क्षेत्रफल सामान है, क्षेत्रफल ΔABC = क्षेत्रफल ΔDEF
सिद्ध: त्रिभुजें सर्वांगसम ΔABC ≅ ΔDEF
जैसा दिया हुआ है की ΔABC और ΔDEF दोनों त्रिभुज समरूप है
इसलिए,क्षेत्रफल का अनुपात इसके संबंधित पक्ष के अनुपात के वर्ग के बराबर है
इसी तरह, हम पाते हैं
DE = AB
DF = AC
चूंकि, ΔABC और ΔDEF में
EF =BC
AB = DE
AC = DF
इसलिए SSS सर्वांगसम से
ΔABC ≅ ΔDEF
एक समबाहु त्रिभुज ABC में भुजा BC पर एक बिंदु D इस प्रकार है कि BD = 1/3BC है । सिद्ध कीजिए कि । 9(AD)2 = 7(AB)2
माना हर एक पक्ष △ABC का 'a' है
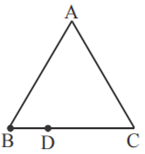
∴ BD = a/3
सिद्ध करना :9 (AD)2 = 7 (AB)2
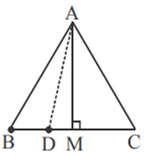
सिद्ध कीजिए की, एक समकोण त्रिभुज में कर्ण का वर्ग शेष दो भुजा के वर्गों के योग के बराबर होता है।
माना ABC एक समकोण त्रिभुज है जिसमें ∠B = 90°
सिद्ध करना:कर्ण2 = लंबाई2 + आधार2
AC2 = AB2 +BC2
अब B से एक लम्ब बनाइए जो BD ⊥ AC
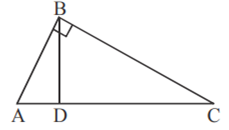
अब त्रिभुज ADB और ABC में,
△ADB ~ △ ABC
Mock Test Series
Sponsor Area
Sponsor Area






 है।
है।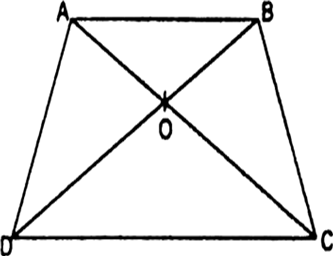
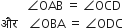
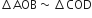


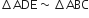 है।
है।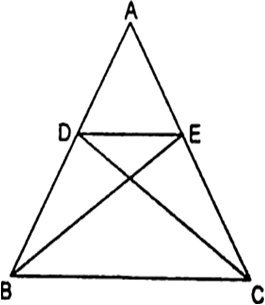



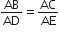
 [ उभयनिष्ट ]
[ उभयनिष्ट ]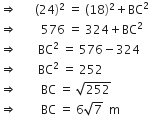
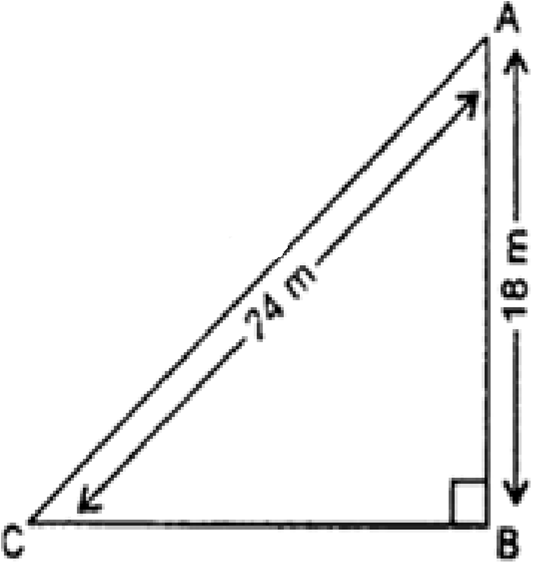
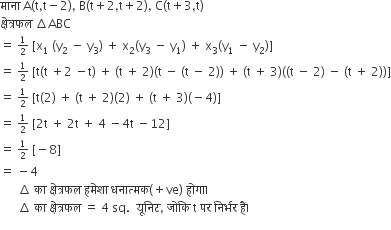
 है। सूर्य का उन्नयन कोण क्या है?
है। सूर्य का उन्नयन कोण क्या है?