एक त्रिभुज ABC की भुजाएँ AB और AC तथा मध्यिका AD एक अन्य त्रिभुज की भुजाओं PQ और PR तथा मध्यिका PM के क्रमश: समानुपाती हैं।दर्शाइए कि ∆ABC~∆PQR है।

Solution

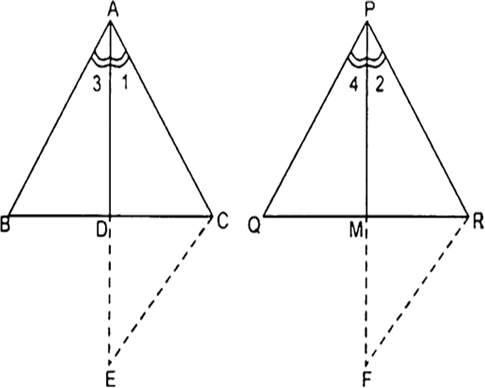
∆ABD और ∆CDE में,
AD = DE
$angle ADB space equals space angle CDE$
और BD = DC    [AD समद्विभाजक है]
   $increment ABD approximately equal to increment CDE$
$rightwards double arrow$ $AB equals CE$
इसी तरह,   $increment PQM space equals space increment RMF$
$rightwards double arrow$    $PQ equals RF$
दिया है कि,
$AB over PQ equals AC over PR equals AD over PM$
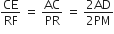
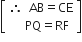
$rightwards double arrow$ $CE over RF space equals space AC over PR space equals space fraction numerator 2 AD over denominator 2 PM end fraction$    $open square brackets table row cell therefore space space AB equals CE end cell row cell space space space space PQ equals RF end cell end table close square brackets$
$rightwards double arrow$ $CE over RF space equals space AC over PR space equals space AE over PF$
$increment ACE space approximately equal to space increment PRF$
$rightwards double arrow$ $angle 1 space equals space angle 2$ ...(i)
इसी प्रकार,
   $space angle 3 space equals space angle 4$ ...(ii)
समीकरण (i) और (ii) को जोड़ने पर
   $angle 1 space plus space angle 3 space equals space angle 2 space plus space angle 4 angle straight A space equals space angle straight P$
∆ABC और ∆PQR में,
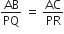
$AB over PQ space equals space AC over PR$
और 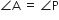$angle straight A space equals space angle straight P$
अत: सिद्ध होता है कि ∆ABC ~ ∆PQR