आकृति में ΔABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD⊥BC, OE⊥AC और OF⊥AB है। दर्शाइए कि
(i) OA² + OB² + OC² - OD² - OE² - OF² = AF² + BD² + CE^2,(ii) AF² + BD² + CE² = AE² + CD² + BF²

Solution

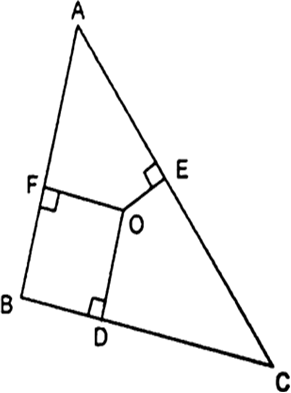
(i) समकोण ΔOFA में,
OA² = AF² + OF² ...(i)
समकोण ΔOBD में,
OB² = OD² + BD² ...(ii)
समकोण ΔOEC में,
OC² = OE² + CE² ...(iii)
समीकरण (i), (ii) और (iii) को जोड़ने पर, हमें प्राप्त होता है:
OA² + OB² + OC² = AF² + OF² + OD² + BD² + OE² + CE²⇒ OA² + OB² + OC² = AF² + BD² + CE² + OD² + OF² + OE²⇒ AF² + BD² + CE² = OA² + OB² + OC² - OD² - OF² - OE²
(ii) AF² + BD² + CE² = (OA² - OE²) + (OB² - OF²) + (OC² - OD²)
= AE² + CD² + BF²अत:, AF² + BD² + CE² = AE² + CD² + BF²

Some More Questions From त्रिभुज Chapter

For Daily Free Study Material Join wiredfaculty

त्रिभुज

Some More Questions From त्रिभुज Chapter

सभी वृत्त ______ होते हैं। (सर्वांगसम, समरूप)

सभी वर्ग ______ होते हैं। (समरूप, सर्वांगसम)

सभी ______ त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)

निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ (ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।

बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

त्रिभुज

आकृति में ΔABC के अभ्यंतर में स्थित कोई बिंदु O है तथा OD⊥BC, OE⊥AC और OF⊥AB है। दर्शाइए कि(i) OA2 + OB2 + OC2 - OD2 - OE2 - OF2 = AF2 + BD2 + CE2,(ii) AF2 + BD2 + CE2 = AE2 + CD2 + BF2

Some More Questions From त्रिभुज Chapter

सभी वृत्त ______ होते हैं। (सर्वांगसम, समरूप)

सभी वर्ग ______ होते हैं। (समरूप, सर्वांगसम)

सभी ______ त्रिभुज समरूप होते हैं। (समद्विबाहु, समबाहु)

निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:(i) समरूप आकृतियाँ (ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।

बताइए कि निम्नलिखित चतुर्भुज समरूप हैं या नहीं:

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

निम्नलिखित युग्मों के दो भिन्न-भिन्न उदाहरण दीजिए:
(i) समरूप आकृतियाँ (ii) ऐसी आकृतियाँ जो समरूप नहीं हैं।