Question
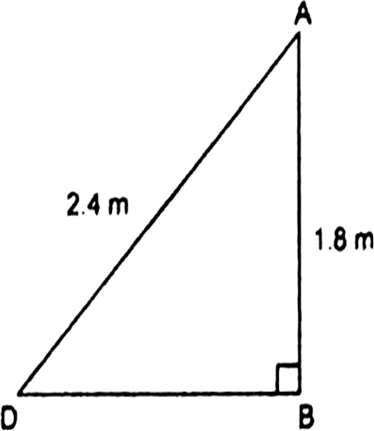
नाज़िमा एक नदी की धारा में मछलियाँ पकड़ रही है। उसकी मछली पकड़ने वाली छड़ का सिरा पानी की सतह से 1.8 m ऊपर है तथा डोरी के निचले सिरे से लगा काँटा पानी के सतह पर इस प्रकार स्थित है कि उसकी नाज़िमा से दूरी 3.6 m है और छड़ के सिरे के ठीक नीचे पानी के सतह पर स्थित बिंदु से उसकी दूरी 2.4 m है। यह मानते हुए कि उसकी डोरी (उसकी छड़ के सिरे से काँटे तक) तनी हुई है, उसने कितनी डोरी बाहर निकली हुई है? यदि वह डोरी को 5cm/s की दर से अंदर खींचे, तो 12 सेकंड के बाद नाज़िमा की काँटे से क्षैतिज दूरी कितनी होगी?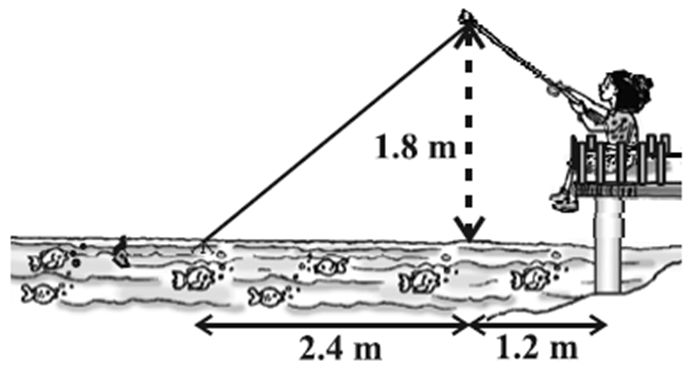
Solution
जो डोरी बाहर है उसकी लंबाई 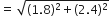
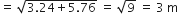
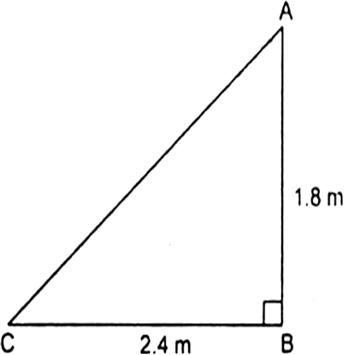
अत: जो डोरी बाहर है उसकी लंबाई = 3m
अब,
12 सेकंड में 5cm/s की दर से खींची गई डोरी की लंबाई
= 5×12 = 60cm = 0.6cm
∴ शेष बची डोरी की लंबाई
= 3.0 - 0.6 = 2.4 m
अब,

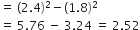

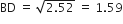 (लगभग)
(लगभग)
अत: 12 सेकंड बाद नाज़िमा की काँटे क्षैतिज दूरी = (1.59 + 1.2)m
= 2.79 m (लगभग)
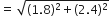
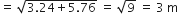

अत: जो डोरी बाहर है उसकी लंबाई = 3m
अब,
12 सेकंड में 5cm/s की दर से खींची गई डोरी की लंबाई
= 5×12 = 60cm = 0.6cm

∴ शेष बची डोरी की लंबाई
= 3.0 - 0.6 = 2.4 m
अब,

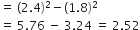

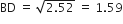 (लगभग)
(लगभग)अत: 12 सेकंड बाद नाज़िमा की काँटे क्षैतिज दूरी = (1.59 + 1.2)m
= 2.79 m (लगभग)



