+91-8076753736[email protected]
logo
logo
-->

त्रिभुज

Question
CBSEHHIMAH10010107
Wired Faculty App

यदि दो समरूप त्रिभुजों के क्षेत्रफल बराबर हों तो सिद्ध कीजिए कि वे त्रिभुज सर्वांगसम होते हैं।

Solution

       increment ABC tilde increment DEF
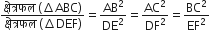
rightwards double arrow   fraction numerator क ् ष े त ् रफल space left parenthesis increment ABC right parenthesis over denominator क ् ष े त ् रफल space left parenthesis increment DEF right parenthesis end fraction equals AB squared over DE squared equals AC squared over DF squared equals BC squared over EF squared
परन्तु   क ् ष े त ् रफल space left parenthesis increment ABC right parenthesis space equals space क ् ष े त ् रफल space left parenthesis increment DEF right parenthesis
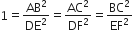
rightwards double arrow  1 equals AB squared over DE squared equals AC squared over DF squared equals BC squared over EF squared
rightwards double arrow        AB squared space equals space DE squared
            AC squared space equals space DF squared
और        BC squared space equals space EF squared
rightwards double arrow          AB space equals space DE
             AC space equals space DF
और         BC space equals space EF
∆ABC और ∆DEF में,
             AB = DE
             AC = DF
और         BC = EF

         increment ABC approximately equal to increment DEF

Some More Questions From त्रिभुज Chapter

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation