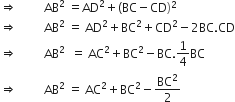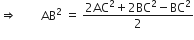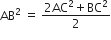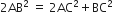Question

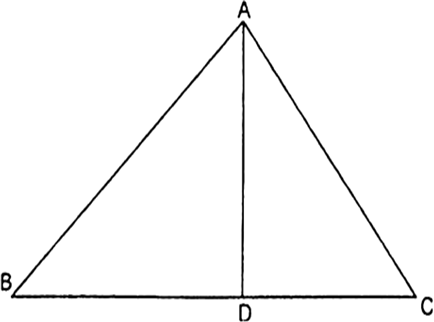
किसी त्रिभुज ABC के शीर्ष A से BC पर डाला गया लम्ब BC को बिंदु D पर इस प्रकार प्रतिच्छेद करता है कि DB = 3CD है। सिद्ध कीजिए कि 2AB²=2AC²+BC² है।

Solution

∵ DB = 3CD [दिया है]
अब, BC = CD + DB
$rightwards double arrow$ BC = CD+ 3CD
$rightwards double arrow$ BC = 4CD
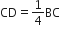
$rightwards double arrow$ $CD equals 1 fourth BC$
समकोण ΔADB में,
AB² = AD² + DB²
$rightwards double arrow space space space space space space space space space AB squared space equals AD squared plus left parenthesis BC minus CD right parenthesis squared rightwards double arrow space space space space space space space space space AB squared space equals space AD squared plus BC squared plus CD squared minus 2 BC. CD rightwards double arrow space space space space space space space space space AB squared space space equals space AC squared plus BC squared minus BC.1 fourth BC rightwards double arrow space space space space space space space space space AB squared space equals space AC squared plus BC squared minus BC squared over 2$
$rightwards double arrow space space space space space space space space AB squared space equals space fraction numerator 2 AC squared plus 2 BC squared minus BC squared over denominator 2 end fraction$
$rightwards double arrow$ $AB squared space equals space fraction numerator 2 AC squared plus BC squared over denominator 2 end fraction$
$rightwards double arrow$ $2 AB squared space equals space 2 AC squared plus BC squared$

For Daily Free Study Material Join wiredfaculty

त्रिभुज

Some More Questions From त्रिभुज Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction