Question
यदि दो समरूप त्रिभुजों के क्षेत्रफल समान हों, तो सिद्ध कीजिए कि वह त्रिभुजें सर्वांगसम होती हैं।
Solution
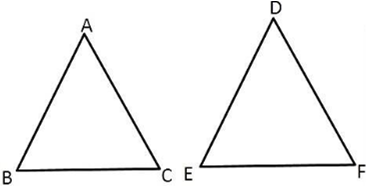
माना ΔABC और ΔDEF दोनों त्रिभुज समरूप है,
ΔABC ~ ΔDEF
माना ΔABC और ΔDEF दोनों त्रिभुज का क्षेत्रफल सामान है, क्षेत्रफल ΔABC = क्षेत्रफल ΔDEF
सिद्ध: त्रिभुजें सर्वांगसम ΔABC ≅ ΔDEF
जैसा दिया हुआ है की ΔABC और ΔDEF दोनों त्रिभुज समरूप है
इसलिए,क्षेत्रफल का अनुपात इसके संबंधित पक्ष के अनुपात के वर्ग के बराबर है
इसी तरह, हम पाते हैं
DE = AB
DF = AC
चूंकि, ΔABC और ΔDEF में
EF =BC
AB = DE
AC = DF
इसलिए SSS सर्वांगसम से
ΔABC ≅ ΔDEF