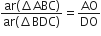Question
आकृति में एक ही आधार BC पर दो त्रिभुज ABC और DBC बने हुए हैं। यदि AD, BC को O पर प्रतिच्छेद करे, तो दर्शाइए कि 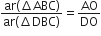 है।
है।
Solution
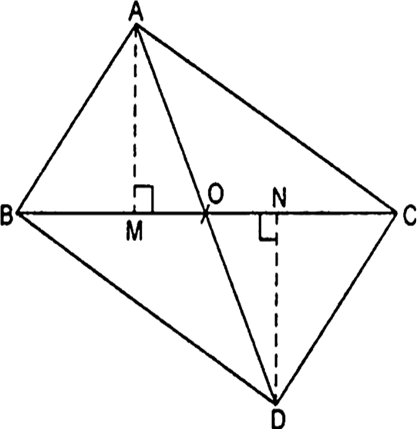
A तथा D से BC पर लंब AM और DN खींचो।
∆AMO और ∆DNO में,

[शीर्षाभिमुख कोण]
∆AMO ~ ∆DNO
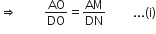
अब,
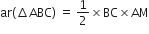
और
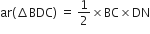
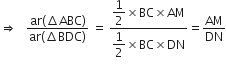
परन्तु

अत: यह सिद्ध होता है कि