Question
आकृत में ABD एक समकोण त्रिभुज है जिसका कोण A समकोण है तथा 
है। दर्शाइए कि
(i) AB2 = BC.BD
(ii) AC2 = BC.DC
(iii) AD2 = BD.CD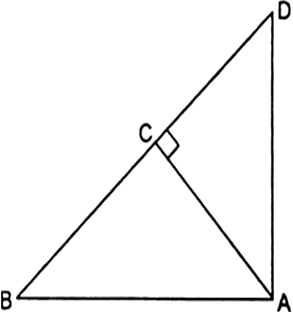
Solution
(i) ∆BAC और ∆BDA में,
...(i)
समकोण ∆ABC में,
...(ii)
समकोण ∆ABD में,
...(iii)
समीकरण और की तुलना करने पर
और, 
[दोनों कोण 90o हैं]
∴ ∆BAC ~ ∆BDA
∴ 
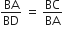
⇒ BA2 = BC.BD
⇒ AB2 = BC.BD
(ii) समकोण ∆ACB और ∆DCA में,
∴ ∆ACB ~ ∆DCA
∴ 
⇒ AC2 = BC.DC
(iii) समकोण ∆ADB और ∆CDA में,
(उभयनिष्ट)
∴ ∆ADB ~ ∆CDA
∴ 
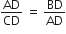
⇒ AD2 = BD.CD
