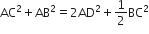Question
आकृति में AD त्रिभुज ABC की एक माध्यिका है तथा AM⊥BC है। सिद्ध कीजिए कि
(i) 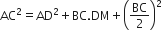
(ii) 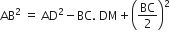
(iii) 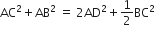

Solution
(i) समकोण ΔACM में,
AC2 = AM2 + MC2
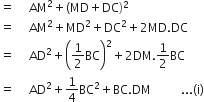
(ii) समकोण ΔABM में,
AB2 = AM2 + BM2
= AM2 + (BD - MD)2
= AM2 + BD2 + MD2 - 2BD.MD
= (AM2 + MD2) + BD2 - 2BD.MD
=
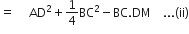
(iii) समीकरण (i) और (ii) को जोड़ने पर
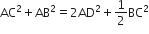
AC2 = AM2 + MC2
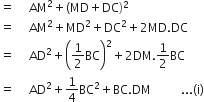
(ii) समकोण ΔABM में,
AB2 = AM2 + BM2
= AM2 + (BD - MD)2
= AM2 + BD2 + MD2 - 2BD.MD
= (AM2 + MD2) + BD2 - 2BD.MD
=

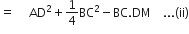
(iii) समीकरण (i) और (ii) को जोड़ने पर