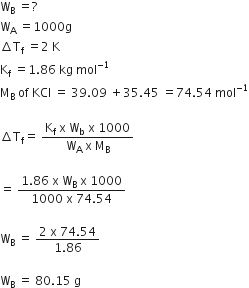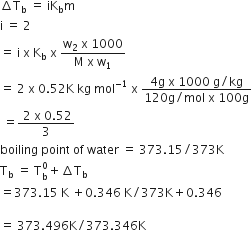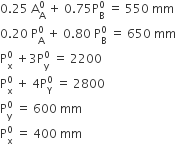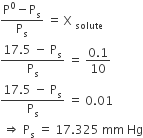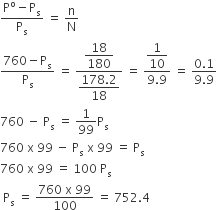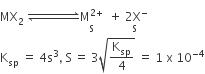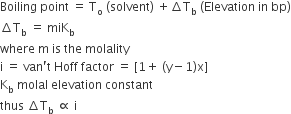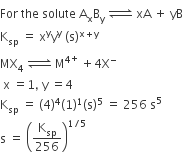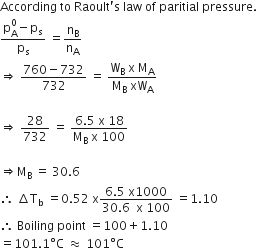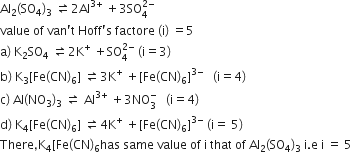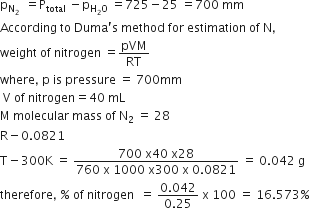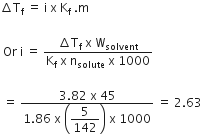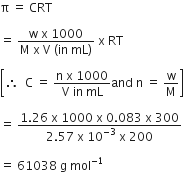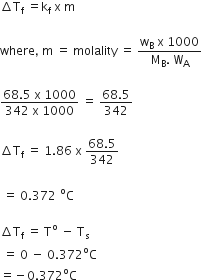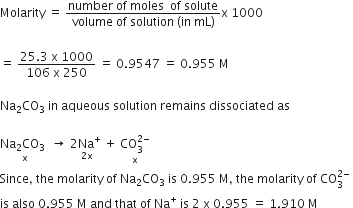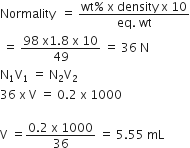Chemistry I Chapter 2 Solutions
Sponsor Area
NCERT Solution For Class 12 Business+studies Chemistry I
Calculate the mass percentage of benzene (C6H6) and carbon tetrachloride (CCl4) if 22 g of benzene is dissolved in 122 g of carbon tetrachloride.
Mass% of carbon tetrachloride = 100 - 15.28
= 84.72%
Calculate the mole fraction of benzene in solution containing 30% by mass in carbon tetrachloride.
Let the total mass of the solution be 100g and mass of benzene be 30 g
therefore mass of tetrachloride= (100-30)g = 70g
Molar mass of benzene,
Calculate the molarity of each of the following solution (a) 30 g of Co(NO3)2.6H2O in 4.3 L solution (b) 30 mL of 0.5 MH2SO4 diluted to 500 mL.
solution;
Molarity (M) is defined as number of moles of solute dissolved in one litre (or one cubic decimetre) of solution.
(a) Mol. mass of
Moles of
Volume of solution = 4.3 L
Molarity,
(b) Number of moles present in 1000 ml of 0.5M H2SO4= 0.5 mol
therefore number of moles present in 30ml of 0.5M H2SO4=mol =0.015mol
therefore molarity =0.015/0.5L
thus molarity is 0.03M
Calculate the mass of urea (NH2CONH2) required in making 2.5 kg 0.25 of molal aqueous solution.
Molality (m) is defined as the number of moles of the solute per kilogram (kg) of the solvent and is expressed as:
Mol. mass of urea
= 14 + 2 + 12 + 16 + 14 + 2
=
Molality (m) =
or Moles of solute
= 0.25 x 0.25 = 0.625
Mass of urea
= Moles of solute x Molar mass
= 0.625 x 60 = 37.5 g
Calculate (a) molality (b) molarity and (c) mole fraction of KI if the density of 20% (mass/mass) aqueous KI is 1.202 g mL-1.
Therefore, Moles of KI in solution

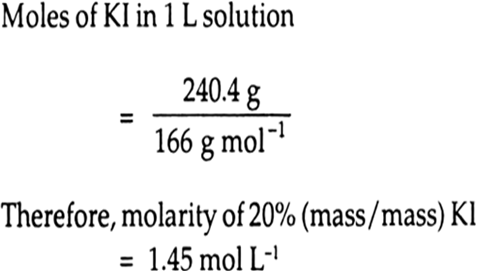
moles of KI = 20/166 =0.12mol
moles of water =80/18 =4.44mol
therefore, mole fraction of KI
=
H2S, a toxic gas with rotten egg like smell, is used for the qualitative analysis. If the solubility of H2S in water at S.T.P. is 0.195 m, calculate Henry's law constant.
It is given that the solubility of H2S in water at STP is 0.195m, i.e., 0.195 mol of H2S is dissolved in1000 g of water.
=
At STP pressure (P) = 0.987bar
According to henry's law p = kH x
Henry’s law constant for CO2 in water is 1.67 x 108 Pa at 298 K. Calculate the quantity of CO2 in 500 mL of soda water when packed under 2.5 atm CO2 pressure at 298 K.
Solution :
given that,
pressure of CO2=2.5atm
1 atm = 1.01325x 105 pa so that
pressure of CO2 = 2.5x1.01325x105pa
= 2.533125 x 105 pa
KH = 1.67 x 108 pa
ACcording to henry's law p= KH*X
or X=P/KH
= 2.533125 x 105/1.67x 108
= 1.52 x 10-3
But we have 500ML odf soda water so that
Volume of water = 500mL
Density of water =1g/ml
mass = volume x density
500 mL of water = 500g of water
molar mass f water (H2O) = 18g mol-1
number of moles =
Vapour pressure of pure water at 298 K is 23.8 mm. 50 g of urea (NH2CONH2) is dissolved in 850 g of water. Calculate the vapour pressure of water for this solution and its relative lowering.
Vapoure pressure of pure water (solvent) at 298 K, p0 = 23.8 mm
Vapour pressure of solution, p = ?
Mass of solvent ,W = 850 g
Mass of solute,M = 50 g
Mol. mass of water (H2O), M = 18 g mol–1
Mol.mass of urea NH2 CO NH2
= 14 + 2 + 12 + 16 + 14 + 2
= 60 g mol–1
According to Raoult's law,
Hence, 23.78 mm Hg. Ans.
Boiling point of water at 750 mm Hg 99.630C. How much sucrose is to be added to 500g of water such that it boils at 1000C.
here, elevation of boiling point = (100+273)-(99.63+273) = 0.37K
mass of water, w1 = 500g
Boiling point of water at 750 mm Hg = 99.630C
or
or
hence , 121.67 g of sucrose is to obtained.
Calculate the mass of ascorbic acid (Vitamin C, C6H8O6) to be dissolved in 75 g of acetic acid to lower its melting point by 1.5 0C. Kf= 3.9 k kg mol–1.
Solution:
Mass of acetic acid W1= 75g
Molar mass of
lowering of melting point ,
Hence, 5.08 g of ascorbic acid is needed to be dissolved.
Calculate the osmotic pressure in pascals exerted by a solution prepared by dissolving 1.0 g of polymer of molar mass 185,000 in 450 mL at 370C.
we have given that
Volume of water, V= 450ml=0.450L
Temperature, T = (37+273)K = 310K
Suppose a solid solution is formed between two substances, one whose particles are very large and the other whose particles are very small. What kind of solid solution is this likely to be?
Amongst the following compunds identify which are insoluble, partially soluble and highly soluble in water?
(i) phenol (ii) toluene (iii) formic acid (iv) ethylene glycol (v) chloroform, (vi) pentanol.
Insoluble: toluene, chloroform.
Partially soluble: phenol, pentanol.
Highly soluble: formic acid, ethylene glycol.
Two liquids A and B boils at 1450C and 1900C respectively. Which of them has a higher vapour pressure at 800C ?
Liquid A has lower boiling point, So it is being more volatile and has high vapour pressure at 800 C
Because vapour pressure has an inverse relation ith boiling point.
Define ‘mole fraction’ of a substance in a solution.
Mole fraction: Commonly used symbol for mole fraction is x and subscript used on the right hand side of x denotes the component.
It is defined as:
Mole fraction of a component =
For example, in a binary mixture, if the number of moles of A and B are nA and nB respectively, the mole fraction of A will be
x =
What is expected value of Van’t Hoff factor for K3 [Fe(CN)6] in dilute solution?
The dissociative equation for K3[Fe(CN6)] can be written as:
therefore , number of particles after dissiociation = 4
so van't hoff factor =4/1 = 4
Sponsor Area
State the formula relating pressure of a gas with its mole fraction in a liquid solution in contact with it.
The most commonly used form of Henry’s law states that “the partial pressure of the gas
in vapour phase (p) is proportional to the mole fraction of the gas (x) in the solution”
Pgas = Mole fraction gas of gas x KH, where KH is Henry law constant
⇒ p = KH.x where ‘x’ is mole fraction.
What would be the value of Van’t Hoff factor for a dilute solution of K2SO4 in water?
Why is the elivation in boiling point of water different in the following solution?
(i) 0.1 molar NaCl solution.
(ii) 0.1 molar sugar solution.
The elevation in boiling point depend on the dissociation of particle in solution.
0.1 M NaCl will dissociate into Na+ and CI– whereas 0.1 M sugar solution will not dissociate. The number of particles are more in NaCl, the elevation in boiling point is higher.
Why does the molality of solution remains unchanged with rise in temperature?
Molality: Molality (m) is defined as the number of moles of the solute per kilogram (kg) of the solvent and is expressed as:
Molality (m) =
molality are independent of temperature, whereas molarity is a function of temperature. This is because volume depends on temperature
and the mass does not.
10 mL of liquid A was mixed with 10 mL of liquid B. The volume of the resulting solution was found to be 19.9 mL. What do you conclude?
Define Henry's law about solubility of a gas in a liquid.
Henry’s law states that “the partial pressure of the gas in vapour phase (p) is proportional to the mole fraction of the gas (x) in the solution” and is expressed as: p = KHx
where KH henry's constant
A and B liquids on mixing produced a warm solution. Which type of deviation is there and why?
The process is exothermic, it means that there is + ve deviation because force of attraction between A-B is more than A-A or B-B.
Why does sugar dissolve in water?
sugar dissolves in water because when a sucrose molecule breaks from the sugar crystal, it is immediately surrounded by water molecules. The sucrose has hydroxyl groups that have a slight negative charge.
The positive charge of the oxygen found in the water molecule binds with the sugar. As the hydration shell forms around the sucrose molecule, the molecule is shielded from other sugar molecules so the sugar crystal does not reform.
Why sugar does not dissolve in Benzene?
sugar does not dissovle in the bezene beacuse of their polar nature.
like dissovle like.
benzene is non polar in nature and gulcose is polar in nature .
What temperature change is expected during the mixing of two liquids whose solution shows a negative deviation from Raoult’s law?
When is value of Van’t Hoff factor more than one?
van't hoff factor depend on the dissociation in case of dissociation, the Van’t Hoff’s factor is more than 1 because the observed molecular mass has a lesser value than the normal molecular mass.
It is in case of strong electrolyte.
Why does the boiling point of a solution exhibit negative deviation from the ideal behaviour?
The boiling point of a solution exhibit negtive deviation from the behaviour Because there is an increase in vapour pressure of the solution. So less energy is not required to equalise the vapour pressure to that of atmospheric pressure.
What is Van’t Hoff factor i of the compound AlCl3?
Van't hoff factor is an integer based on the number of particles that substance will dissociate into .
AlCl3 dissociate into 4 . thus van't hoff factor of i =4
Define Van’t Hoff factor ‘i’?
van’t Hoff factor, to account for the extent of dissociation or association. This factor i is defined as:
For association ‘i’ is less than unity and for dissociation ‘i’ is greater than unity.
Define an ideal solution.
Answer:
The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is
also zero, i.e.,
ΔmixH = 0, ΔmixV = 0
Differentiate between molarity and Molality?
Molarity: Molarity (M) is defined as number of moles of solute dissolved in one litre (or one cubic decimetre) of solution,
express unit in L-1
Molality: Molality (m) is defined as the number of moles of the solute per kilogram (kg) of the solvent and is expressed as:
Express unit in Kg-1
molality are independent of temperature, whereas molarity is a function of temperature. This is because volume depends on temperature and mass does not.
What is the Van’t Hoff factor of a compound which undergoes tetramerisation in an organic solvent?
The van't hoff factor is an integer based on the number of particles that substance will dissociate into.
A compound undergoes tetramerisation have
Van’t Hoff factor, i = 4.
State Raoult’s law for dilute solutions?
The relative lowering of vapour pressure is equal to the mole fraction of solute in solution.
Define Molality in terms of elevation in boiling point?
For dilutesolutions the elevation of boiling point (ΔTb) is directly proportional to the molal concentration of the solute in a solution. Thus
ΔTb ∝ m
or ΔTb = Kbm
Here m (molality) is the number of moles of solute dissolved in 1 kg of solvent and the constant of proportionality, Kb is called Boiling Point
Elevation Constant or Molal Elevation Constant . The unit of Kb is K kg mol-1.
What are azetropes? Give an example.
An azeotrope is a mixture of two or more liquid whose proportions cannot be altered by simple distillation.
For example, H2O (4.13%) + C2H5OH (95.87%) mixture boils at a constant temperature of 78.150C.
What is the sum of the mole fraction of all the components in a three component system?
Some of the mole fractions of all the components is unity.
x1 + x2 + x3 = 1.
Sponsor Area
What is meant by vapour pressure? What is effect of temperature on it?
It can be defined as the pressure exerted by vapour over the liquid surface is called vapour presure.
vapour pressure is directly proportional to temperature.
What do you understand by ‘colligative’ property?
Colligative properties are those properties of solution that depend on the number of solute dissolved in solution. But not the identites of the solute.
Colligative properties have been used to determine the molar mass of solutes.
Why is vapour pressure of solution of glucose in water is lower than that of water?
The vapour pressure of pure solvent decrease when a non- volatile solute is added to the solvent this is because on adding the solute, a fewer number of water molecules are present at the surface which can evaporate as some of the surface area is occupied by non- volatile solute molecules thereby decreasing the vapour pressure of the solution thus the vapour pressure of the solution of the glucose in water lower than that of water.
What are isotonic solutions? How do they differ from hypotonic and Hypertonic solutions?
Answer:
A hypotonic solution in which it contain more solute than solvent.example a lot of salt (solute)
dissovled in water (solvent)
isotonic solution in which solute and solvent are equally distrubuted for example a cell normally wants to remain in an isotonic solution where concentration of liquid inside it is equal to the concentration of the liquid outside of it.
hypertonic solution in which contains more solvent than solute.
What is the relationship between the eubllioscopic constant and the elevation in boiling point of the solution?
the elevation of boiling point (ΔTb) is directly proportional to the molal concentration of
the solute in a solution. Thus
ΔTb ∝ m
or ΔTb = Kbm
Here m (molality) is the number of moles of solute dissolved in 1 kg
of solvent and the constant of proportionality, Kb is called Boiling Point
Elevation Constant or Molal Elevation Constant (Ebullioscopic
Constant). The unit of Kb is K kg mol-1.
How is the alcohol and water are miscible in all proportions?
It is because of the polar nature of both compounds . Due to having same polarity they combine to form H- bond with water.
Why do gases nearly always tend to be less soluble in liquids as the temperature is raised?
Gas in liquid it generate a small quantity of heat so we can say that dissolution of gas in a liquid is a exothermic reaction.
How is osmotic pressure related to the concentration (or number of moles) of a solute in solution?
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:
Π = C R T
Here Π is the osmotic pressure and R is the
gas constant.
Π = (n2 /V) R T
Here V is volume of a solution in litres containing n2 moles of solute.
If w2 grams of solute, of molar mass, M2 is present in the solution, then n2 = w2 / M2 and we can write
Thus, knowing the quantities w2, T, Π and V we can calculate the
molar mass of the solute.
What is the effect of temperature on solubility of salt in water?
Temperature does effect the solubility of any solid solute in a solution,like in the case of salt in water.the effect of temperature depends on the nature of reaction.if the reaction is an endothermic reaction,then the increase in temperature has a positive effect and the solubility increases.if it is an exothermic process,then the increase in the temperature would not favour the solubity of the solute.
For Salt + Water Solution ΔH = + ve or for endothermic dissolution of salt, the solubility increases with temperature. Where as for exothermic dissolution. Salt + Water → Solution. ΔH = – ve > the solubility decreases with temperature.
What happens to vapour pressure of solution if table sugar or table salt is added to water?
Define Raoult’s law?
Raoult’s law states that "for a solution of volatile liquids the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
p1 ∝ x1
and p1 = x1
where is vapour pressure in the pure state
Why is the osmotic pressure measurement preferred for determining molecular mass of proteins?
Therefore, to determine the molecular mass of proteins, osmotic pressure is preferred.
Why does the boiling point of a solvent increase by the presence of a solute in it?
A liquid boils when its vapour pressure is equal to the atmospheric pressure. When a nonvolatile solute is added to a solvent, its vapour pressure gets lowered. Therefore, higher temperature will be required to attain the same vapour pressure. Therefore, the solution of a nonvolatile solute will boil at higher temperature than the solvent.
A deci-molar solution of K4 [Fe(CN)6] is 50% dissociated at 300 K. Calculate the osmotic pressure of solution (R = 0.082)/L atm K–1)?
The given complex is ionsiable and it dissociates as follow
(1-a) 4a a
Where a is the degree of dissociation of a complex.
intial moles of complex =1
moles after dissociation of the complex = 1-a + 4a+a = 1+4a
Pobserve/ Pnormal= (1+4a)/1
Dissociation takes place only 50% a= 0.50
P/2.462 = 1+(4 x 0.50)
p/2.462 = 1+2
p/2.462=3
p= 2.462x 3
p=7.386 atm
Why is osmotic pressure considered a colligative property?
colligative property depend on the number of solute particles irrespective of their nature relative to the total number of particles present in the solution.
Osmotic pressure depends upon the number of particles of solute, i.e., molarity of solute. Therefore, it is considered as colligative property.
Why is an increase in temperature observed on mixing chloroform with acetone?
When chloroform is added to acetone there are new forces of attraction due to hydrogen bonding between acetone and chloroform.
ΔHmix is negtive because energy is released due to increase in the attractive forces, therefore dissolution is the exothermic process . hence temperature is increases.

What are the units of molal elevation constant?
the units of elevation constant is K kg mol–1.
The observed boiling point of mixture of two volatile liquids is more than that calculated. What type of deviation is noticed?
when boiling point of mixture of two volatile liquid is more than Negative deviation shown.
Why is CaCl2 used to remove snow on roads?
CaCl2 used to remove snow on the road because
Addition of CaCl2 lowers the freezing point of water.
Why is freezing point depressed when a non-volatile solute is added?
When non-volatile solute is added to solvent, the vapour pressure of solution becomes less and at a lower temperature, the vapour pressure of solution and solvent in a solid state will become equal, i.e., freezing point is lowered.
Why is boiling point elevated when a non-volatile solute is added?
When non-volatile solute is added, the vapour pressure of solution is less. Therefore, it is to be heated at higher temperature so that it boils, i.e., boiling point is raised.
The osmotic pressure of polymers (Macro-molecules) are determined by osmotic pressure and not by other colligative properties. Explain.
The osomatic pressure of polymer are determined by osmotic pressure because osmotic pressure is measured at room temperature whereas macro-molecules undergo change in structure at high temperature.
What happens when blood cells are placed in pure water?
When blood cells are placed in pure water than
Due to osmosis, water molecules move into the blood cells through the cell walls. As a result the blood cells swell and may even burst.
What are the factors on which the vapour pressure of a liquid depends?
Answer:
The vapour pressure of a liquid depend on following factor.
(i) Temperature.
(ii) Type of solute in solution (i.e., whether the solute is volatile or non-volatile.
State the conditions under which the Raoult’s law holds good.
The Raoult's law holds good on the following condition:
(i) the two volatile components of the solution form an ideal solution.
(ii) the solution containing non-volatile solute is very dilute.
What are the different types of azetropes? Give one example of each.
Answer:
There are two types of azetropes:
(i) Minimum boiling azetropes →Ethanol + water.
(ii) Maximum boiling azetropes →Chloroform + acetone.
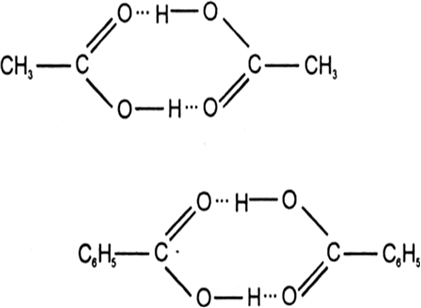
Give an example of a compound in which hydrogen bonding results in the formation of a dimer.
Acetic acid and benzoic acid exist as dimer due to hydrogen bonding when dissolved in an organic solvent.
State any two characteristics of an ideal solution.
Answer:
The two characteristics of ideal solution is:
(i) An ideal solution follows Raoult’s law and the components can be separated by fractional distillation.
(ii) ΔHmix = 0,
ΔVmix = 0,
A-A, B-B and A-B interactions of same length.
What are the value ΔH, ΔV and Ptotal for a solution showing negative deviation from identity? Give one example.
Answer:
A solution showing negtive deviation:
ΔH = –ve,
ΔV = – ve, Ptotal < P0A XA + P0B XB
Example: Solution of chloroform and acetone.
If the membrane used in determination of osmotic pressure is slight leaking, how will it influence the measured value of osmotic pressure?
Solvent will diffuse into solution and concentration of solute will decrease. Therefore, measured value of osmotic pressure will be lower.
Why do doctors advice gargles of saline water in case of soring of throat?
Doctor advice gargle by saline water in case of sore throat. Relief is observed in sore throat by saline water due to osmosis process
Saline water is hypertonic solution. Therefore, fluids causing irritation in throat comes out with saline water.
A person suffering from high blood pressure should take less common salt in the food. Why?
Common salt (contains Na+ and CI–) dissociates into ions in the blood and increases the osmotic pressure of blood. Therefore, it increases the blood pressure which is harmful.
What type of deviation (+ ve or – ve) is expected of a solution obtained by adding conc. H2SO4 to water?
Adding conc. H2SO4 to water Heat is liberated in the process of dissolution, ΔH < 0. The solution formed will show negative deviation from Raoult’s law, A-B attractions > A-A and B-B attractions.
Which process is used in large scale desalination of sea water?
In the large scale desalination of sea water
Reverse Osmosis process is used.
Which of the following has higher vapour pressure at same temperature: CH3OH (b. p. 640.50C) and C2H5OH (b.p. 78.30C)?
Vapour pressure is related with the molecular weight, lower the molecular weight higher the vapour pressure. since CH3OH has less molecular weight as compare to C2H5OH thus CH3OH has higher vapour pressure than C2H5OH at the same temperature.
Why is the freezing point depressed when a non-volatile solute is dissolved in a liquid solvent?
When a non- volatile solute is dissolved in a liquid solvent freezing point depressed Because of decrease in vapour pressure.
Which of the two has higher osmotic pressure: 1 M glucose solution or 1 M NaCl solution at the same temperature?
1 M NaCl solution has higher osmotic pressure (almost double as NaCl dissociated in two ions).
When a liquid A is mixed with liquid B, the resulting solution is found to be cooler. What do you conclude about the nature of the solution?
The solution shows a positive deviation. Absorption of heat takes place. A-B interactions are weaker than A-A and B-B interactions.
Sponsor Area
What will happen to the value of colligative property of a solution if the weight of solute dissolved is doubled and weight of solvent taken is halved?
The colligative property increase as we increase the concentration of solute.
The value of colligative property will be four times because the concentration will become four times.
50 mL of a liquid A when mixed with 50 mL of liquid B, the resulting volume is 100.5 ml. What do you think about nature of solution?
The solution will show a positive deviation from Raoult’s law. Increase in volume means A-B attractions are weaker than A-A and B-B attractions.
Mention two biological phenomena regulated by osmosis in plants and animals.
Answer:
(i) Plants absorb water from the soil through their roots due to osmosis.
(ii) In animals, water moves into different parts of body due to osmosis.
What happens if pressure greater than osmotic pressure is applied on the solution separated by a semi-permeable membrane from the solvent?
On applying greater pressure than osmotic pressure the reverse phenomenon takes place.
10 mL of a liquid A was mixed with 10 mL of liquid B. The volume of resulting solution was found to be 19.9 mL. What do you conclude?
It shows that solution is non ideal showing – ve deviation in which force of attraction increases, volume decreases.
Ethanol is an organic compound, yet it is freely miscible with water. Why?
Ethanol is a polar oragnic compound thus it form hydrogen bond with water.

In cold countries, ethylene glycol is added to water radiators of cars during winter. Why?
This causes lowering in freezing point of water and therefore water does not freeze in radiators.
What is a semi-permeable membrane?
A membrane is a thin layer that may or may not allow particles to pass through it. Permeable is defined as a membrane that can be crossed by particles, ions, or water.
Semi permeable means, It is a membrane which permits the solvent molecules but not solute molecules to pass through it from a dilute solution to concentrated solution. Example: A film of gelatinous precipitate of cupric ferrocyanide, Cu[Fe(CN)6].
Define the term solution. How many types of solutions are formed? Write briefly about each type with an example.
Answer:
A solution is a homogenous mixture of two or more than two substances whose composition can change within a certain limits. A solution of two substances is called binary solution.
In solution, the component that present in small amount is known as solute and the component present in larger amount known as solvent.
Nine kinds of solution are possible.
(i) Gas in gas. When one gas is mixed with another gas, it is called solution of gas in gas. Example : Air is a mixture of nitrogen and oxygen.
(ii) Liquid in gas. When liquid is mixed with large amount of gas, it is called liquid in gas solution. Example: Moisture (water in air).
(iii) Solid in gas. When small amount of solid particles are dispersed in gas, it is called solution of solid in gas. Example: Smoke.
(iv) Gas in liquid. When gas is dissolved in liquid, it is called gas in liquid solution. Examples: CO2 gas dissolved in water, oxygen dissolved in water.
(v) Liquid in liquid. When a liquid is miscible with another liquid, it forms solution of liquid in liquid. Examples. Ethanol dissolved in water, methanol dissolved in water.
(vi) Solid in liquid. When solid is dissolved in water, the solution is called solid in liquid. Examples: Cane sugar dissolved in water, sodium chloride dissolved in water.
(vii) Gas in solid. When gas is present, the solution is called gas in solid. Example: H2 gas in palladium.
(viii) Liquid in solid. When liquid is present in solid, the homogeneous mixture is called solution of liquid in solid. Example: Amalgam of mercury with sodium.
(ix) Solid in solid. When solid is dissolved in another solid, the homogeneous mixture is called solution of solid in solid. Examples: Alloys are solid in solid solution, copper dissolved in gold.
Define the following terms:
Mole fraction
mole fraction can be defined as :
Mole fraction of a component =
for example
Mole fraction. The ratio of the moles of a component A to the total moles of the solution is called the mole fraction of A. It is denoted by symbol x. For a binary solution of components A and B Mole fraction of A = xA
Mole fraction of B = xB
Define the following terms:
Molality
Molality. The moles of the solute dissolved in one kilogram of the solvent is called the molality of the solution.
Moality = m =
∵
Define the following terms:
Molarity
Molarity: The concentration expressed as the moles of solute per litre of solution is the molarity. It is denoted by M.
A solution of one molar concentration is represented by 1 M, a two molar solution by 2 M and a one tenth molar solar solution is represented by 0.1 M.
Define the following terms:
Mass percentage.
Mass percentage: It is the amount of solute in grams dissolved per 100 g of solution, e.g., 5% solution sodium carbonate mass 5 g of solid sodium carbonate is present in 100 g of solution.
What role does the molecular interaction play in solution of alcohol and water?
Answer:
In both the components, water (A component) and alcohol (B component), the molecules are hydrogen bonded, i.e., A-A as well as B-B interactions are mainly H-bonds forces. When these two components are mixed to form the solution, due to molecular collisions A-A and B-B interactions are broken down and new interactions of the type A-B are formed. A-B interactions are also mainly H-bonds i.e., the molecules of one liquid will tend to break the hydrogen bonds in the molecules of other liquid and vice-versa. A-B interactions formed will be weaker than A-A and B-B types of of interactions as the alcohol and water solution show positive deviation and it will lead to increase in volume (ΔVmix is + ve).
Why do gases always tend to be less soluble in liquids as the temperature is raised?
Answer:
According to le Chatelier's principle when we increase the temperature in a exothermic reaction , the reaction will move to back ward direction that means solution will dissociate and will give gas .Hence with the rise of temperature gas will less soluble.
For most of gases like N2, O2, He etc. the value of Henry's constant, KH increases with temperature and as a result of this solubility of gases decreases with increase of temperature. We know, at given temperature.
Partial pressure of gas in solution = KH x mole fraction of gas in sol. KH depends on the nature of gas. For example, KH value of O2 at 293 K is 34.86 while at 393 K it is 46.82 kilo bar.
State Henry’s law and mention some important applications.
Answer:
Henry’s law states that the solubility of a gas in a liquid is directly proportional to pressure of the gas; temperature constant.
Mathematically, P = KH x
where
x=mole fraction of gas in solution
P is partial pressure of gas,
KH is Henry's constant.
Applications:
(1) Henry's law finds various applications in industry and enables us to explain and understand some biological phenomena. The some of important applications are : CO2 solubility in soft drinks, beverages, soda water etc. is increased by applying high pressure and bottles are sealed under high pressure.
(2) For deep divers, oxygen diluted with less soluble He gas is used as breathing gas and it minimises the painful effects due to higher solubility of N2 gas in blood.
(3) In lungs, where oxygen is present in air with high partial pressure, haemoglobin combines with O2 to form oxyhaemoglobin. In tissues where partial pressure of O2 is low, oxyhaemoglobin releases the oxygen for utilisation in cellular activities.
What is meant by positive and negative deviations from Raoult’s law and how is the sign of Δmix H related to positive and negative deviations Raoult’s law?
Answer:
According to Raoult's law, the partial vapour pressure of each component in any solution is directly proportional to its mole fraction.
The solution which obeys Raoult's law over enitre range is known as ideal solution.
The solution which do not obeys Raoult's law is known as non- ideal solution.
Non-ideal solution have vapour pressure either higher or lower is predicted by raoult's law
If the vapour pressure is higher then solution is said to exhibit positive deviation, And if the vapour pressure is lower than the solution than it said to be negtive deviation.
Positive Deviation from Raoult’s law. In those non-ideal solutions, when partial pressure of component ‘A’ in the mixture of ‘A’ and ‘B’ is found to be more than that calculated from Raoult’s law. Similarly, the partial vapour pressure of component ‘B’ can be higher than calculated from Raoult’s law.
This type of deviation from ideal behaviour is called positive deviation from Raoult’s law,
e.g., water and ethanol, chloroform and water, ethanol and CCl4, methanol and chloroform, benzene and methanol, acetic acid and toluene, acetone and ethanol, methanol and H2O.
For positive deviation ΔHmixing > 0. (+ ve)
Negative Deviation from Raoult’s law. When the partial vapour pressure of component ‘A’ is found to be less than calculated from Raoult’s law on adding the second component ‘B’. When A is added to B, the partial vapour pressure of solution is less than that of ideal solution of same composition. Boiling point of such a solution is relatively higher than the boiling point of A and B respectively. This type of deviation from ideal behaviour is known as negative deviation from Raoult’s law e.g., chlorofom and acetone, chloroform and methyl acetate, H2O and HCl, H2O and HNO3 acetic acid and pyridine, chloroform and benzene.
For negative deviation ΔHmixing < 0.
Methanol is soluble in water but insoluble in octane. Explain briefly.
Solubility of a substance is its maximum amount that can be dissolved in a specified amount of solvent at a specified temperature. It depends
upon the nature of solute and solvent as well as temperature and pressure. In general, a solute dissolves in a solvent if the intermolecular interactions are similar in the two or we may say like dissolves like.
Methanol and water both are polar and hydrogen bond forming molecules. Thus, they will form homogeneous solution. Whereas octane is non-polar molecule and will not form solution with methanol.
Given below is the sketch of a plant for carrying out a process.
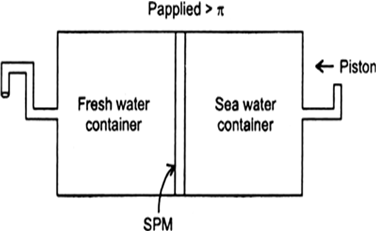
(i) Name the process occurring in the above plant.
(ii) To which container does the net flow of solvent take place?
(iii) Name one SPM which can be used in this plant.
(iv) Give one potential use of the plant.
Answer:
(i) Reverse osmosis.
(ii) Pure water is forced out of the solution to pass through the pores of the membrane in the opposite direction.
(iii) Parchment or cellophone.
(iv) This process is used in desalination to get salt-free water from sea water.
Prove that the relative lowering of vapour pressure is equal to the mole fraction of non-volatile solute in the solution.
Answer:
Raoult established that the lowering of vapour pressure depends only on the concentration of the solute particles and it is independent of their identity.
establishes a relation between vapour pressure of
the solution, mole fraction and vapour pressure of the solvent, i.e.,
.................1
The reduction in the vapour pressure of solvent (Δp1) is given as:
In a solution containing several non-volatile solutes, the lowering of the vapour pressure depends on the sum of the mole fraction of different solutes.
Equation 3 can be written as :
The expression on the left hand side of the equation as mentioned
earlier is called relative lowering of vapour pressure and is equal to
the mole fraction of the solute. The above equation can be written as:
Here n1 and n2 are the number of moles of solvent and solute respectively present in the solution. For dilute solutions n2 < < n1, hence neglecting n2 in the denominator we have
hence proved
Explain why freezing point of a solvent is lowered on dissolving a non-volatile solute into it? Give an important application of the phenomenon of depression in freezing point.
When a non-volatile solute is added its vapour pressure is lowered and at a lower temperature, the vapour pressure of solid and liquid solvent will be equal i.e., depression in freezing point takes place. The application of ΔTf is used as antifreeze so that water does not freeze especially in cold countries.
Give one example each of miscible liquid pairs showing positive and negative deviatins from Raoult’s law. Give one reason for such deviations.
Answer:
According to Raoult's law the partial vapour pressure of each volatile compound in any solution is directly proportional to its mole fraction
if the vapour pressure is higher then solution is said to exhibit positive deviation
Positive deviation is shown by ethanol and water, cyclohexane and ethanol, acetone and diethylether etc.
Reasons:
(i) A—B interaction is weaker than A—A or B—B in positive deviation.
If the vapour pressure is lower then solution then solution is said to exhibit negtive deviation.
Negative deviation is shown by chloroform and acetone, methanol and acetic acid, H2O and HCl, H2O and HNO3 etc.
Reason:
(ii) A—B interaction is stronger than A—A or B—B in negative deviation.
Show that the relative lowering of vapour pressure of a solution containing a nonvolatile solute is equal to the mole fraction of the solute in the solution?
Answer:
Raoult established that the lowering of vapour pressure depends only on the concentration of the solute particles and it is independent of their identity.
establishes a relation between vapour pressure ofthe solution, mole fraction and vapour pressure of the solvent, i.e.
Lowering of vapour pressure
=
Lower of vapour pressure
or
Which type of deviation is shown by the solution formed by mixing cyclohexane and ethanol?
Hydrogen bonds exist among the molecules of ethanol (i.e., strong forces). When cyclohexane is added to ethanol, the cyclohexane molecule will come in between the ethanol molecules and disturb the hydrogen bondings. The forces between ethanol and cyclohexane will be weaker than the previous forces (H-bonding), hence there will be positive deviation.
Why should a solution of a non-volatile solute boil at a higher temperature ? Draw the diagram to prove your point?
Boiling point is that temperature at which the vapour pressure of the solution becomes equal to the external pressure since on adding a nonvolatile solute, the vapour pressure of the solution gets lowered, therefore, it will boil at a higher temperature.
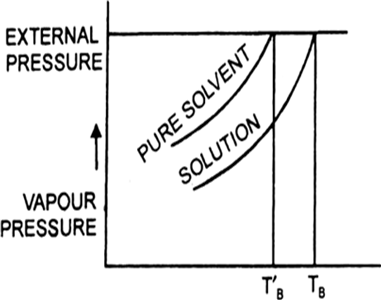
(a) Draw a labelled diagram to show the change in vapour pressure of a solvent, when a non-volatile solute is added to it.
(b) Show that the change in boiling point of the solvent in this diagram?
(a) It is found that the boiling point of the solution is always higher than that of the pure solvent. The elevation in boiling point is the increase in boiling point when a non-volatile solute is added to a solvent.
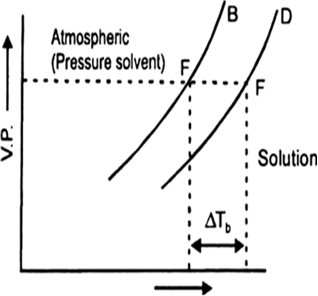
(b) In the above diagram ΔTb indicates the change (increase) in boiling point of solvent.
Illustrate elevation in boiling point with the help of vapour pressure temperature curve of a solution. Show that elevation in boiling point is a colligative property?
Answer:
ΔTb = T2 – T1
ΔTb ∝ m
ΔTb = Kb x m
Here m (molality) is the number of moles of solute dissolved in 1 kg of solvent and the constant of proportionality, Kb is called Boiling Point Elevation Constant or Molal Elevation Constant.
Since ΔTb depends on molality of solution and not on nature of solute, therefore, ΔTb is a colligative property.
Why should the solution of a nonvolatile solute freeze at a lower temperature? Draw a neat diagram to prove your point.
Answer:
The lowering of vapour pressure of a solution causes a lowering of the freezing point compared to that of the pure solvent.
According to Raoult’s law, when a non-volatile solid is added to the solvent its vapour pressure decreases and now it would become equal to that of solid solvent at lower temperature. Thus, the freezing point of the solvent decreases.
T0f is the freezing point of pure liquid solvent. Tf is the freezing point of solution.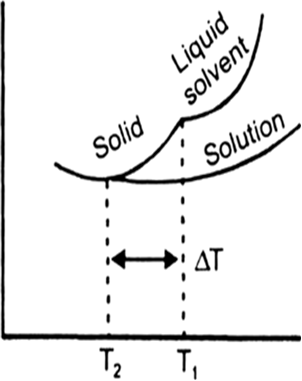
What is the Van’t Hoff factor? How does is modify the equation for the elevation of boiling points?
Modified equation for the elevation of boiling point
ΔTb = i Kbm
Sometimes the molecular mass determined from colligative properties of solutions, show abnormal values. Explain?
Collegative properties of solution are the properties which depend upon the number of particles present in the solution. When the solute does not undergo any chemical/physical change, the molecular mass of the solute as obtained from the colligative properties is equal to its stoichiometric value.
Therefore in many cases where the solute associate or dissociate in solution certain abnormal values of colligative properties are obtained the value of molecule masses calculated based on colligative properties in such cases will also be abnormal.
What are ideal and non-ideal solutions? Mention one nearly ideal solution.
Answer:
The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is
also zero, i.e.,
ΔmixH = 0, ΔmixV = 0
ideal behaviour of the solutions can be explained by considering two components A and
B. In pure components, the intermolecular attractive interactions will be of types A-A and B-B, whereas in the binary solutions in addition
to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal
solution. example are Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, etc
When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution.
example Mixtures of ethanol and acetone.
Define vapour pressure of a liquid. What happens to the vapour pressure of a liquid when (a) a volatile solute dissolves in it and (b) a non-volatile solute dissolves in it?
Answer:
Vapor pressure or equilibrium vapor pressure is defined as the pressure exerted by a vapor in thermodynamic equilibrium with its condensed phases (solid or liquid) at a given temperature in a closed system.
(a) When a volatile solute is dissolved in a liquid total vapour pressure is given by the sum of total vapour pressure of both the solvent and solute ie.,
P = PA + PB.
(b) When a non-volatile solute is dissolved in a liquid, the vapour pressure of liquid decreases and this lowering of vapour pressure is proportional to the mole fraction of solute added to it.
What is osmotic pressure? How is it dependent on the number of moles of a solute?
The minimum excess pressure that has to be applied on the solution to prevent the entry of the solvent in to the solution through the semi-premeable membrane is called the osmotic pressure. It is given by:
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:
Π = C R T
Here Π is the osmotic pressure and R is the
gas constant.
Π = (n2 /V) R T
n is the number of moles of solute.
v is volume of solution.
r is the universal gas constant.
T is the absolute temperature.
State Raoult’s law. If AT is the elevation of boiling point of a solvent and m is the number of moles of solute per kg of solvent, what is the realationship between T and m?
pA ∝ xA
or
where P0A is the vapour pressure of the pure solvent.
PA is the vapour pressure of the solution.
XB is the mole fraction of non-volatile solute.
Thus, according to Raoult’s law, the relative lowering of vapour pressure is equal to the mole-fraction of the solute in solution.
(a) What are non-ideal solution?
(b) What role does the molecular interaction play in deciding the vapour pressure of solutions (i) alcohol and kerosene (ii) Chloroform and acetone.
Answer:
When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution.
(a) Non-ideal solutions are these solutions which
(i) do not follow Raoult’s law.
(ii) ΔHmix ≠ 0.
(iii) ΔVmix ≠ 0.
(iv) The force of attraction between A-A and B-B is not equal to A-B.
(b) In alcohol and acetone, force of attraction is less than alcohol and alcohol molecules as well as acetone and acetone molecule, therefore, vapour pressure increases.
In chlorofom and acetone, force of attraction increases due to intermolecular H-bonding, therefore, vapour pressure decreases.
Why do colligative properties of an electrolyte solution of a given concentration are found to be larger than those of a non-electrolyte solution of the same concentration?
The colligative properties of solution depend on the total number of solute particles present in solution. Since the electrolytes ionise and give more than one particle per formula unit in solution, the colligative effect of an electrolyte solution is always greater than that of a non-electrolyte of the same molar concentration.
Discrepancies arise when solute particles are present in either associated or in the dissociated form. Consider benzoic acid molecules present as dimers in C6H6. The number of solute particles is half, therefore value of Tf for benzoic acid (dissolved in benzene) would be half the normal value. During dissociation of NaCl into Na+ and CI–1 ions in aqueous solution, presence of twice the number of ions cause a doubling of depression/elevation (AT) of freezing/boiling point.
Explain the following phenomena:
(i) Hemolysis
(ii) Crenation.
Answer:
(i) Hemolysis: The red blood cells are protected from the external environment by a semipermeable membrane. The red blood cells are placed in a hypotonic solution. Because the hypotonic solution is less concentrated than the interior of the cell, water moves into the cell. The cell swells and eventually burst, releasing hemoglobin and other molecules. This process is called hemolysis.
(ii) Crenation: When a bacterial cell is placed in a hypertonic (high concentration) sugar solution, the intracellular water tends to move out of the bacterial cell to be more concentrated solution by osmosis. This causes the cell to shrink and eventually, to stop functioning. This process is called crenation.
Why do we observe abnormal molecular masses?
Answer:
We observe abnormal molecular masses when the solute is an electrolyte and undergo either into association or dissociation.
One unit of an electrolyte compound separates into two or more particles when it dissolves and colligative properties depends on the number of solute particles.
Each NaCl unit dissociates into two ions-Na+ and CI–. Thus, the colligative properties of a 0.1 m solution of NaCl should be twice as great as those of a 0.1 m solution containing a non-electrolyte, such as glucose or sucrose.
How does osmotic pressure depend on molality of the solution?
Answer:
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus: Π = C R T
Here Π is the osmotic pressure and R is the gas constant.
Π = (n2 /V) R T
Here V is volume of a solution in litres containing n2 moles of solute. If w2 grams of solute, of molar mass, M2 is present in the solution, then n2 = w2 / M2 and we can write,
in a dilute aqueous solution molarity is equal to molality.
c = m when p = 1 and solution is dilute.
The osmotic pressure will increase with an increase in molality of the solution at a given temperature.
The molar mass of acetic acid determined from the measurement of a colligative property is greater than its formula molar mass. Explain why?
Answer:
The colligative properties of solution depend on the total number of solution.
since the eletrolytes ionise and give more than one particle per formula unit in solution the colligative effect of an eletrolyte solution is alaways greater than that of a non electrolyte of the same molar concentration.
The molar mass of acetic acid in a solution of benzene solvent is greater than its formula molar mass because two CH3COOH molecules form a dimer (CH3COOH)2 in solution. But we know that the molar mass is defined as the mass of 6.023 x 1023 particles of the substance. In case of a normal solute like CH3COOH, the molar mass of acetic acid is equal to the mass of 6.023 x 1023 molecules of formula CH3COOH. While in solution the solution dimerises and becomes a bigger molecule like (CH3COOH)2. Now in this case the molar mass of the solute is equal to the mass of 6.023 x 1023 units of formula (CH3COOH)2. Naturally, this molar mass is larger than the normal formula molar mass. In case of association, Van’t Hoff factor is less than 1, therefore,
MB (abnormal) > MB (normal) when i < 1.
Sponsor Area
Explain why solvent-solvent, solute-solute and solute-solvent interactions are important in determining the extent to which a solute dissolves in a solvent.
The process of a solute dissolving in a solvent is called dissolution. Dissolution depend on the temperature because increasing temperture dissolution is also increase.
Dissolution also depend on the nature of the solute and solvent.
In the dissolution process, solute-solute, solvent-solvent interactions are established. The solubility of a solute thus, depends on the strength of new solute-solvent interactions relative to the strengths of solute-solute and solvent-solvent interactions.
A peeled egg when dipped in water swells, while in saturated salt solution it shrinks. Why?
In the first case endo-osmosis occurs because solution inside egg is concentrated one. In later case exo-osmosis occurs because solution outside egg is concentrated one.
Suggest the most important type of intermolecular attractive interaction in the following pairs.
(i) n-hexane and n-octane.
(ii) I2 and CCl4.
(iii) NaCl O4 and water.
(iv) methanol and acetone.
(v) acetonitrite (CH3 CN) and acetone (C3H6O).
Answer:
(i) The intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B.
(ii) A-B interactions are weaker than those between A-A or B-B.
(iii) A-B interactions are more than those between A-A and B-B.
(iv) A-B interactions are less than A-A and B-B interactions.
(v) A-B interactions are more than A-A and B-B interactions.
Based on solute-solvent interactions, arrange the following in order of increasing solubility in n-octane and explain cyclohexane, KCl, CH3OH, CH3CN.
n- octane is non-polar solvent therefore the solubility of a non-polar solute is more in n- octane solvent.
The order of increasing solubility is :
KCl<CH3OH<CH3CN< cyclohexane.
The depression in freezing point of water observed for the same amount of acetic acid, trichloroacetic acid and trifluoroaacetic acid increases in the order given. Explain briefly.
Answer:
Among H,Cl and F, Hydrogen is least electronegtive while F is most electronegtive than Cl and H.
Thus F can withdraws more electron towards itslef more than Cl and H. So trifluoroacetic acid can easily lose the H+ ions. i.e.
trifluroacetic acid ionize to the larger extent .
Now more the ion produces the greater is the dpress ion of the freezing point
Hence, the depression of freezing point increase in order :
Acetic acid<trichloracetic acid < trifluroacetic acid
Vapour pressures of pure acetone and chloroform at 328 k are 741.8 nm Hg and 632.8 mm Hg respectively. Assuming that they form ideal solution over the entire range of composition, plot Ptotal , Pchlroform and Pacelone as a function of Xactone. The experimental date observed for different composition of mixture is:
|
100 x xacetone |
0 |
11.8 |
23.8 |
36.0 |
50.8 |
58.2 |
64.5 |
72.1 |
|
Pacetone / mm Hg
|
0 |
54.9 |
110.1 |
202.4 |
327.7 |
405.9 |
454.1 |
521.1 |
|
Pchloroform/ mm Hg |
632.8 |
548.1 |
469.4 |
359.7 |
257.7 |
193.6 |
161.2 |
120.7 |
Plot this data also on the same graph paper, indicate whether it has positive deviation or negative deviation from the ideal solution.
 It has negative deviation from the ideal solution.
It has negative deviation from the ideal solution.State Raoult’s law for solutions of volatile liquid components. Taking a suit example, explain the meaning of positive deviation from Raoult’s law.
Answer:
Raoult’s law states that the partial vapour pressure of a component of a solution at a given temperature is equal to the product of the vapour pressure of the pure component at that temperature and its mole fraction in the solution.
Positive Deviation from Raoult’s law: In those non-ideal solutions, when partial pressure of component ‘A’ in the mixture of ‘A’ and ‘B’ is more than that calculated from Raoult’s law. Similarly, the partial vapour pressure of component ‘B’ can be higher than calculated from Raoult’s law. This type of deviation from ideal behaviour is called positive deviation from Raoult’s law, e.g., water and ethanol, chloroform and water, ethanol and CCl4, methanol and chloroform, benzene and methanol, acetic acid and toluene, acetone and ethanol, methanol and H2O.
For positive deviation ΔHmixing > 0.
State the law co-relating the pressure of a gas and its solubility in a liquid. State an application of this law.
Answer:
Henry’s law states that the solubility of a gas in a liquid is directly proportional to pressure of the gas keeping temperature constant.
Mathematically, P = KH x
x mole fraction of gas in solution
P is partial pressure of gas,
KH is Henry's constant.
Applications: Henry's law finds various applications in industry and enables us to explain and understand some biological phenomena. The some of important applications are: CO2 solubility in soft drinks, beverages, soda water etc. is increased by applying high pressure and bottles are sealed under high pressure.
Define the term “osmotic pressure”. Describe how the molecular mass of a substance can be determined on the basis of osmotic pressure measurement.
Answer:
Osmotic pressure: Osmotic pressure is the minimum pressure that should be applied to the more concentrated solution to prevent osmosis.
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T.
Thus: Π = C R T
Here Π is the osmotic pressure and R is the gas constant.
Determination of osmotic pressure: Barkley and Hartley’s method: The apparatus consists of a porous pot containing copper ferrocyanide deposited in its wall (acts as semipermeable membrane) and fitted into a bronze cylinder to which is fitted a piston and a pressure gauge (to read the applied pressure).
The pot is fitted with a capillary indicator on left and water reservoir on right. Pot is filled with water while the cylinder is filled with a solution whose osmotic pressure is to be measured. Water tends to pass into the solution through the semipermeable membrane with the result that the water level in the indicator falls down. External pressure is now applied with piston so as to maintain a constant level in the indicator. This external pressure is osmotic pressure.
If the membrane used was a slightly, leaky, then the measured valued of osmotic pressure will not be definite.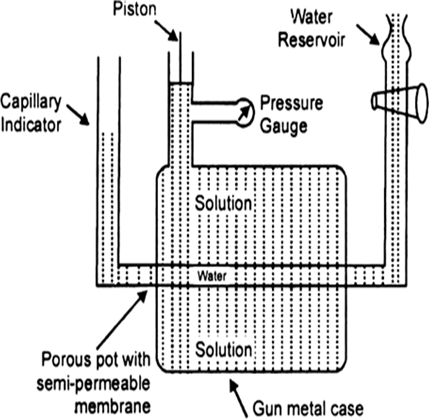
Fig. Barkley and Hartley’s apparatus.
Concentrated nitric acid used in the laboratory work is 68% nitric acid by mass in aqueous solution. What should be molarity of such sample of the acid if the density of solution is 1.504 g mL–1?
68% by mass implies that 68 g of HNO3 are present in 100 g of solution.
Volume of solution =
Molar mass,
A solution of glucose in water is labelled as 10% W/W, what would be the molality and mole fraction of each component in the solution? If the density of the solution is 1.2 g mL–1, then what shall be the molarity of the solution?
Consider 100 g of 10% solution of glucose whose conc. is 10% W / W.
Mass of solution = 100 g
Mass of glucose = 10 g
Mass of solvent = 100 – 10 = 90 g
Molar mass of glucose,
C6H12O6 = 6 x 12 + 12 x 1 + 6 x 16
= 72 + 12 + 96 = 180 g / mol
Molality =
Moles of
Moles of glucose,
Mole fraction of glucose,
Mole fraction of water
Density of sol = 1.2 g mol L
Therefore, volume of solution
Molarity =
How many mL of 0.1 M HC1 are required to react completely with 1 g mixture of Na2CO3 and NaHCO3 containing equimolar amounts of both?
Answer:
Let ‘a’ moles of Na2CO3 and a moles of NaHCO3 are present in 1 g equimolar mixture of two. Then we can write (a x 106) + (a x 84) = 1
(Molar masses are : Na2CO3 = 106 and NaHCO3 = 84)
a = 5.26 x 10–3 ‘a’ moles of Na2CO3 = 2
a equivalent of Na2CO3 ‘a’ moles of NaHCO3
=a equivalent of NaHCO3 (2a x 1000) + (a x 1000) = 0.1 x V
∴
[where V is volume of HCl (0.1 M)] Substituting the value of a, we have
1 x 10–4 = 3a = 3 x 5.26 x 10–3
V = 157.8 mL
A solution is obtained by mixing 300 g of 25% solution and 400 g of 40% solution by mass. Calculate the mass percentage of the resulting solution.
Mass of solute in 300 g of solution of 25% conc.
Mass of solvent in 300 g of solution
= 300 – 75 = 225 g Moles of solute in 400 g of solution of 40% conc.
Mass of solvent in 400 g of solution
= 400 – 160 = 240 g Total mass of the solute
= 75 + 160 = 235 g Total mass of solvent
= 225 g + 240 g = 465 g Total mass of solution
= 300 + 400 = 700 g Therefore, composition of solute in solution after mixing =
Percentage composition of solvent in solution after mixing
An antifreeze solution is prepared from 222.6 g of ethylene glycol (C2H6O2) and 200 g of water. Calculate the molality of the solution. If the density of the solution is 1.072 g mL–1, then what shall be the molarity of the solution?
Answer:
Consider ethylene glycol as solute and water as a solvent.
Weight of solute, WB = 222.6 g
Molar mass, MB = 24 + 6 + 32 = 62
WB = 200 g = 0.200 kg.
Moles of solute,
Molaity of ethylene glycol in H2O
Total mass of solution
= 222.6 + 200 = 422.6 g
Density of solution
= 1.072 g/ ml Volume of solution
Molarity of solution,
A sample of drinking water was found to be severely contaminated with chloroform (CHCl3), supposed to be a carcinogen. The level of contamination was 15 ppm (by mass):
(i) express this in percent by mass
(ii) determine the molality of chloroform in the water sample.
Answer:
(i) 15 ppm of CHCl3 in water means that there is 15 g of CHCl3 in 106 g of water (1 million = 106)
Percentage of CHCl3
(ii)
Here we have already find the mass % is 15 x 10-4
Number of moles of solute = mass of solute / molar mass
number of moles of CHCl3 =
Molality, m of CHCl3 in drinking water sample
molaity = 1.266 x 10-5 / 0.1 = 1.266 x 10-4 mol Kg-1
The partial pressure of ethane over a solution containing 6.56 x 10–3 g of ethane is 1 bar. If the solution contains 5.00 x 10–2 g of ethane, then what shall be the partial pressure of th gas?
P(C2H6 )= KH x mole fraction of gas in sol
An aqueous solution of 2% non-volatile solute exerts a pressure of 1.004 bar at the normal boiling point of the solvent. What is the molar mass of the solute?
Given values
Here w1 and w2 are the masses and M1 and M2 are the molar masses of the solvent and solute respectively.
Heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components are 105.2 kPa and 46.8 kPa respectively. What will be the vapour pressure, in bar of a mixture of 26.0 g of heptane and 35.0 g of octane?
Answer:
We have given,
Molar mass of heptane,
C7H16 = 100 g mol–1
Molar mass of octane,
C8H18 = 114 g mol–1
Moles of heptane
Similarly, Moles of octane
Mole fraction heptane
Mole fraction of octane
Partial vapour pressure = Mole fraction x Vap.
Pressure of pure component.
Partial vapour pressure of heptane
= 0.456 x 105.2 = 47.97 kPa
Partial vapour pressure of octane
= 0.543 x 46.8 = 25.4 kPa
Total vapour pressure of solution = 73.08 kPa.
The vapour pressure of water is 12.3 kPa at 300 K. Calculate vapour pressure of 1 molar solution of a non-volatile solute in it.
1 molar solution means 1 number of moles of the solute per kilogram (kg) of the solvent. Mole fraction of solute.
or
Calculate the mass of a non-volatile solute (molecular mass 40 g mol–1) which should be dissolved in 114 g octane to reduce its vapour pressure to 80%.
molar mass of solute, M2 =40g mol-1
mass of octane, w1= 114g
molar mass of solute, M1 = 114 g mol-1
Let the vapour pressure of pure octane be
then, the vapour pressure of the octane after dissolving the non volatile solute is
applying the relation,
or
or
If the density of some lake water is 1.25 g mL–1 and contains 92 g of Na+ ions per kg of water, calculate the molality of Na+ ions in the lake.
Answer:
number of moles present in 92g of Na+ ion.
=92/23g mol-1 = 4mol
Molality,
No. of gm moles of solute = 92/23 = 4
Wt. of water (solvent) = 1 kg
If the solubility product of CuS is 6 x 10–16, calculate the maximum molarity of CuS in aqueous solution.
Solubility product of CuS, Ksp = 6x10-16
Suppose solubility of CuS is x mol–1
This would give x mol–1 of Cu2+ ions and x mol L–1 of S2– ions on dissociation.
[Cu2+] = x mol–1
[S2–] = x mol–1
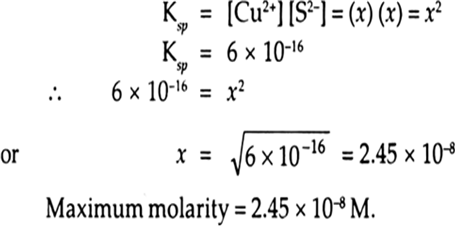
Calculate the mass percentage of aspirin (C9H8O4) in acetonitrile (CH3CN) when 6.5 of C9H8O4 is dissolved in 400 g of CH3CN.
Answer:
Mass of solute = 6.5 g
Mass of solution = 450 + 6.5 = 456.6 g
Calculate the molarity of 1 litre solution of 93% H2SO4 (weight/volume). The density of solution is 1.84 gm L–1.
(i) Volume of solution = 1 L = 1000 mL
Density of solution = 1.84 g mL–1
Mass of solution = V x d
= (1000 mL) x 1.84 mL–1
= 18540 g
Mass of H2SO4 = 93g/100mL
93 x 10 = 930 g
Mass of solvent (water)
= 1840 – 930 = 910 g.
(ii) Molarity (m)
Calculate the amount of benzoic acid (C6H5COOH) required for preparing 250 mL of 0.15 M solution in methanol.
Answer:
Mol. mass of benzoic acid, C6H5COOH
= 6 x 12 + 5 x 1 + 12 + 16 + 16 + 1
= 72 + 5 + 12 + 16+16 + 1
= 122 g mol–1
by using formula;
here x= amount of substance required
Amount of benzoic acid required
Calculate the depression in the freezing of water when 10 g of CH3CH2CHCICOOH is added to 250 g of water. Ka = 1.4 x 10–3, Kf = 1.86 K kg moL–1.
Answer:
We have given
w2 = 10g
w1 = 250
Kf = 1.86k kg mol-1
M2 = 122.5
Mol. mass of CH3CH2CHCICOOH
Nalorphene (C19 H21 NO3) similar to morphine, is used to combat withdrawl symptoms in narcotic users. Dose of nalophene generally given is 1.5 mg. Calculate the mass of 1.5 x10–3 m aqueous solution required for the above dose.
Molar Mass of C19 H12 NO3
= 19 x 12 + 21 x 1 + 14 + 48
= 228 + 21 + 14 + 48
= 311 g mol–1
by = 1000.467 g solution
for 0.0015 g mass of nalorphene contain
by = 1000.467 × 0.0015/0.467
= 3.21 g.
Vapour pressure of water at 293 K is 17.535 mm Hg. Calculate the vapour pressure of water at 293 K when 25 g of glucose is dissolved in 450 g of water.
Vapour pressure of water
Mass of glucose W2 = 25 g
mass of water w1 = 450g
we know that
mass of glucose = 180gmol-1
molar mass of glucose =25/180g mol-1
mass of water = 18 g
molar mass of water M2 = 450/18 g mol-1
apply equation we get,
or
or
or
or
Henry's law constant for the molality of methane in benzene at 298 K is 4.27 x 105mm Hg. Calculate the solubility of methane in benzene at 298 K under 760 mm Hg.
p = 760mmHg
KH = 4.27 x 105
According to Henry's law
v = KHx
kH = 4.27 x 105 mm Hg,
p = 760 mm
or
Determine the amount of CaCl2 (i = 2.47) dissolved in 2.5 litre of water such that its osmotic pressure is 0.75 atm at 270C.
CaCl2 → Ca2+ + 2Cl–
T = 273 + 27 = 300 K,
M = 1 x 40 + 2x 35.5 = 111g mol-1
V = 2.5 L
i = 2.47
osmatic pressure,
amount of calcium chloride dissolved is 3.42g
Determine the osmotic pressure of a solution prepared by dissolving 25 mg of K2SO4 in 2 litre of water at 250 C, assuming that it is completely dissociated.
When K2SO4 is dissolved in water , K+ and ion produced
total number of ion produced 3
therfore, i = 3
given that
w = 25 mg = 0.025g
T = 250C + 273 = 298 K
Also we know that
R = 0.0821 L atm K-1 mol-1
M= (2 x39)+(1x 32)+(4x16)
Benzene and toluene form iedal solution over the entire range of composition. The vapour pressure of pure benzene and naphthalene at 300 K are 50.71 mm Hg and 32.06 mm Hg respectively. Calculate the mole-fraction of benzene in vapour phase if 80 g of benzene is mixed with 100 g of toluene.
Mole of benzene
Mass of Toluene
Mole fraction of benzene
1-XBenzene = 1 - 0.486 = 0.514
Use the formula if Henry law
Partial vapour pressure of benzene, PBenzene = poBenzene × XBenzene
PBenzene=0.487 × 50.71 = 24.645 mm Hg
Partial pressure of Toluene, P toluene = 0.514 × 32.06 = 16.48 mmHg
Use the formula of mole fraction using partial pressure
Plug the values we get
Mole fraction of benzene = 24.645 /(24.645 + 16.48 )
= 24.645/41.123 = 0.60
100 g of liquid A (molar mass 140 g mol–1) was dissolved in 1000 g of liquid B (molar mass 180 g mol–1). The vapour pressure of pure liquid B and found to be 500 torr. Calculate the vapour pressure of pure liquid A and its vapour pressure in the solution if the total vapour pressure of the solution is 475 torr.
Heptane and Octane form an ideal solution at 373 K. The vapour pressures of the pure liquids at this temperature are 105.2 K Pa and 46.8 K Pa respectively. If the solution contains 25 g of heptane and 28.5 g of octane, calculate
(i) Vapour pressure exerted by heptane.
(ii) Vapour pressure exerted by solution.
(iii) Mole fraction of octane in the vapour phase.
Components A (Heptane, )
Components of B
No. of moles of heptane,
No. of moles of octane,
Total moles in solution,
(i) Vapour pressure exerted by heptane
where is mole fraction of component A
(ii) Vapour pressure of octane
Total vapour pressure of solution
(iii) Mole fraction of octane
Ethylene glycol (molar mass = 62 g mol–1) is a common automobile auto freeze. Calculate the freezing point of a solution containing 12.4 g of this substance in 100 g of water. Would it be advisable to keep the substance in the car radiator during summer?
Wb = 12.4
nB= 62g/mol
WA = 100g
or
Freezing point of the solution
= 273.15 - 3.72 = 269.43K.
Calculate the temperature at which a solution containing 54 g of glucose, C3H12 O6, in 250 g of water will freeze. [Kf for water = 1.86 K kg mol–1]
by applying the formula
Substituting the values
Freezing point of solution
= 273 - 2.232 = 270.768 K.
How is osmotic pressure of a solution determined ? If the membrane used was slightly leaky, how will it influence the measured value of osmotic pressure?
Osmotic pressure of a solution containing 7 g of a protein per 103 ml of solution is 25 mm Hg at 310 K. Calculate the molecular mass or the protein. (R = 0.0821 L atm K–1 mol).
Answer:
Osmotic pressure: Osmotic pressure is the minimum pressure that should be applied to the more concentrated solution to prevent osmosis.
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus: Π = C R T
Here Π is the osmotic pressure and R is the gas constant.
(a) Measurement of Osmotic Pressure. Different methods are employed for the measurement of osmotic pressure in the laboratory but Berkley and Hartley's method gives the best results. The apparatus consists of a porous pot containing copper ferrocyanide deposited in its wall (acts as semi-permeable membrane) and fitted into a bronze cylinder to which is fitted a piston and a pressure gauge (to read the applied pressure).
The pot is fitted with a capillary indicator on left and water reservoir on right. Pot is filled with water while the cylinder is filled with a solution whose osmotic pressure is to be measured. Water tends to pass into the solution through the semipermeable membrane with the result that the water level in the indicator falls down. External pressure is now applied with piston so as to maintain a constant level in the indicator. This external pressure is osmotic pressure.
If the membrane used was a slightly, leaky, then the measured valued of osmotic pressure will not be definite.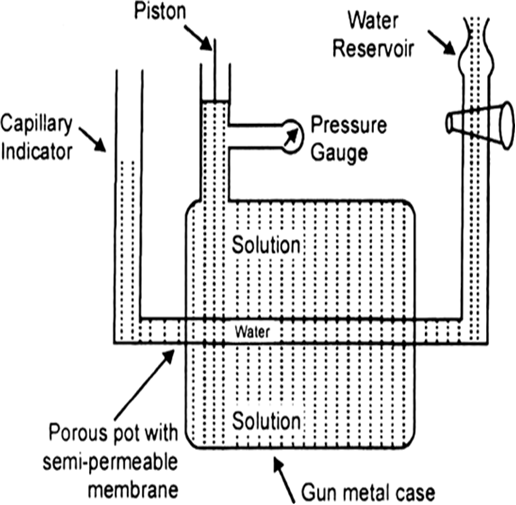
Fig. Berkley and Hartley's apparatus.
(b)
we have given that
mB = 7g
R=0.0821 L atm K-1 mol
Define vapour pressure of a liquid. What happens to the vapour pressure when (a) a volatile solute dissolves in the liquid and (b) the dissolved solute is non-volatile?
Every pure liquid exerts a vapour pressure in the space above it. This is the vapour pressure of the solvent over it at that particular temperature. It depends upon the nature of the solvent and the temperature.
(a) If a volatile solute is dissolved, vapour pressure of the solvent is increased.
(b) However, if a non-volatile solute is dissolved in it, the vapour pressure of the solution is lowered. This is because, in a solution, the percentage of the volatile solvent molecules, which only contributes towards vapour pressure is diminished.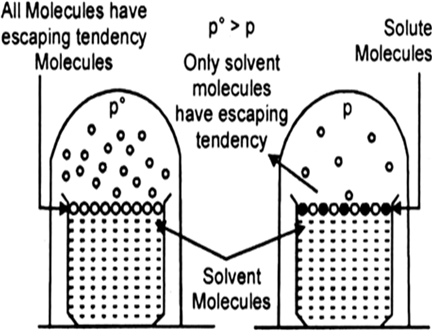
Fig. Decrease of vapour pressure when a non-volatile solute is added to the solvent.
Since, the solute molecules are non-volatile and show no measurable tendency to escape from the solution as vapour, consequently, the vapour pressure of a solution is always lower than that of its solvent.
Raoult’s gave a relation between the relative lowering of vapour pressure and the mole fraction of the solute. Mathematically:
(mole fraction of the solute)
Using the above equation, we can determine the molecular weight of the solute, when the lowering in v.p. is known, when a known weight of the solute w, dissolved in a known wt. of the solvent W.p0 is the vapour pressure of the pure solvent and m and M are the molecular weights of solute and solvent respectively.
Discuss the various types of plots between the partial vapour pressure and the mole fractions of two components of the completely miscible liquids in a solution.
When the partial vapour pressures of different (two) miscible liquids are plotted against their compositions (mole fractions), following three types of vapour pressure-composition (p – x) curves are obtained.
(a) Type-I: When the vapour pressures of the mixture lie between the vapour pressure of pure components : In such cases the solution obeys the Raoult’s law (ideal solution) i.e., the partial vapour pressure of each component (pc) is obtained by the relation.
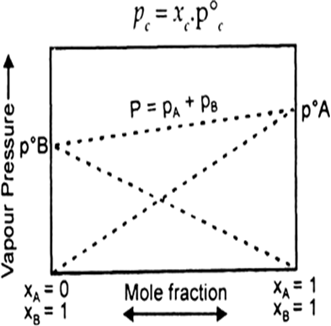
Fig. Solution obeying Raoult’s law.
Where xc is the mole fraction of that component and p0c the vapour pressure of that component in pure form. In such cases, p-x curve is always a straight line. The total vapour pressure of the solution is equal to the sum of the partial vaour pressures of all components.
Examples: Solution of benzene-toluene, chlorobenzene bromobenzene, hexane-heptane.
(b) Type-II : When the observed vapour pressure of the solution is greater than that of calculated vapour pressure from the Raoult’s law : In such cases partial vapour pressure of each component is found to be more than expected on the basis of the Raoult’s law. The total vapour pressure of the solution is also greater than the vapour pressure corresponding to the ideal solution. At a certain composition the total vapour pressure of the solution will be the highest (maximum) which is greater than the vapour pressure of either of the pure liquids (components) at this components the boiling point of the solution will be lowest. This type of deviation from Raoult’s law is known as positive deviation and the system exhibits a maximum value of vapour pressure at certain composition. At this composition both the liquids boil at same (constant) temperature (minimum boiling azeotropes). In figure point C, corresponds the composition of the two liquids which boils at lowest temperature. For example, alcohol-water mixture having the composition of 95.59% alcohol and 4.41 water boils at 78.130C. This composition is called azeotropic mixture.

Fig.p-x curve showing maximum in the total vapour pressure curve.
Example: Ethanol-water solution. Acetone-carbon disulphide solution. Chloroform-ethanol solution.
(c) Type-III: When the observed vapour pressure of the solution is less than that of calculated from Raoults law: In such cases the partial vapour pressure of any component is found to be less than the expected vapour pressure on the basis of Raoult’s law. Similarly, the total vapour pressure of the solution is also less than that of expected value according to Raoult’s law. At a certain composition the total vapour pressure of such solution will be lowest (minimum). At this composition the boiling point of the solution will be highest (maximum) and both the component will boil at same temperature without the change in the composition. Such composition corresponds to the maximum boiling azeotropic mixture. For example a mixture of 20.24% of HCl and 79.76% water forms an azeotropic mixture which boils at 1100C, without the change in composition. In figure, point C, corresponds the composition of azeotropic mixture. This type of deviation in Raoult’s law is known as negative deviation.
Example : Solution of water-HCl, chloroform-benzene, acetone-aniline.
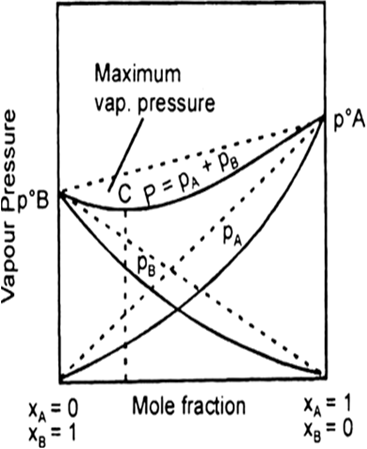
Fig. p-x curve showing minimum in the total vapour pressure curve.
Derive the relationship between relative lowering of vapour pressure and mole fraction of a volatiles liquid.
Answer:
for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
pA ∝ xA
pA x xA where pA is vapour pressure of solvent having mole fraction xA.
PA = P0A x A
But xA + xB = L
∴ xA = 1 – xB
When xB is mole fraction of non-voltile solute B
Pa = P0A (1–xB)
= p0A – p0A x B
Total vapour of solution is equal to pA as nonvolatile solute does not have any vapour pressure.
i.e., Total vapour pressure,
Benzoic acid completely demerises in benzene. What will be the vapour pressure of solution containing 61 g of benzoic acid per 500 g benzene when the vapour pressure of pure benzene at the temperature of experiment is 66.6 torr?
No. of moles after dissociation
Mole fraction of benzoic acid
Mole fraction of benzoic
or
or
Which of the following solution has the lowest freezing point and why? 0.1m glucose.01 m KCl, 0.1 m Na2SO4.
Derive a relationship between mole fraction and vapour pressure of a compound of an ideal solution in the liquid phase and vapour phase.
Answer:
for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
pA ∝ xA
Where only solvent is volatile
pA a xA where p A is vapour pressure of solvent having mole fractionxA,
But xA + xB = 1
xA = 1 – xB where xB is mole fraction of non-volatile solute B
pA = p0A (1 – xB)
= p0A – p0A x B
Total vapour pressure
Solution containing non-volatile solute : For a solution of non-volatile solid in a liquid the vapour pressure contribution by the non-volatile solute is negligible. Therefore the partial vapour pressure of a solution containing a non-volatile solute is equal to the product of the vapour pressure of the pure liquid (solvent p0A) and its mole fraction in solution.
PA = P0A x xB ....(i)
xB is the mole fraction of the non-volatile solute
B, then xA + xB = 1
xA = 1 – xB ....(ii)
Substituting the value of xA fromeq. (ii) into eq. (i), we get, pA = p0A (1 – xB) = p0A – p0A x B
The limiting value of the Van’t Hoff factor for Na2SO4.10H2O is________.
Van't hoff is the number of species formed by a compound on dissociation/associatio in aqueous medium.
Na2SO4.10H2O ----> 2Na+ + + 10H+ + 10OH-
total 23
Define mole fraction of a component in a solution.
Amount of mole of a constituent divided by the total amount of moles of all constituent in a mixture.
Mole fraction of a component =
State Henry's law about the solubility of a gas in a liquid.
Henry's law state that
the partial pressure of the gas in vapour phase (p) is proportional to the mole fraction of the gas (x) in the solution” and is expressed as:
p = KH x
Here KH is the Henry’s law constant
Define an ideal solution.
The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e.,
ΔmixH = 0, ΔmixV = 0
Why is Van’t Hoff factor introduced in the equation for colligative properties of solutions?
van’t Hoff factor modifies the equations for colligative
properties as follows:
Relative lowering of vapour pressure of solvent,
Elevation of Boiling point, ΔTb = i Kb m
Depression of Freezing point, ΔTf = i Kf m
Osmotic pressure of solution, Π = i n2 R T / V
thus it shows that van't hoff factor depend on solute such that it is a colligative properties.
How is osmotic pressure dependent upon number of moles of solute?
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus: Π = C R T
Here Π is the osmotic pressure and R is the gas constant.
Π = (n2 /V) R T
Here V is volume of a solution in litres containing n2 moles of solute. If w2 grams of solute, of molar mass, M2 is present in the solution, then n2 = w2 / M2 and we can write,
in a dilute aqueous solution molarity is equal to molality.
c = m when p = 1 and solution is dilute.
The osmotic pressure will increase with an increase in molality of the solution at a given temperature.
Define Van’t Hoff factor. What is its value for a non-electrolytic solution?
Van’t Hoff introduced a factor ‘i’ called Van’t Hoff’s factor, to express the extent of association or dissociation of solutes in solution. It is ratio of the normal and observed molecular masses of the solute, i.e
In case of association, observed molecular mass being more than the normal, the factor i has a value less than 1. But in case of dissociation, the Van’t Hoff’s factor is more than 1 because the observed molecular mass has a lesser value than the normal molecular mass. In case there is no dissociation the value of ‘i’ becomes equal to one.
Give one example each of the following solutions:
(i) Liquid in liquid, (ii) Gas in gas.
Answer:
(i) Liquid in liquid: Ethanol dissolved in water
(II) Gas in gas : Mixture of oxygen and nitrogen gases
How is osmotic pressure related to the concentration of the solution?
Answer:
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. thus
Π = C R T
Here Π is the osmotic pressure and R is the
gas constant.
Π = (n2 /V) R T
Here V is volume of a solution in litres containing n2 moles of solute.
If w2 grams of solute, of molar mass, M2 is present in the solution, then
n2 = w2 / M2 and we can write
Thus, knowing the quantities w2, T, Π and V we can calculate the molar mass of the solute.
What are azeotropic solutions?
Answer:
Azeotropes are a mixture of at least two different liquids. Their mixturecan either have a higher boiling point than either of the components or they can have a lower boiling point. Azeotropes occur when fraction of the liquids cannot be altered by distillation.
example ethanol (95.5%) + water (4.5) mixture boils at 351.5k
Write the mathematical expression relating the molality and the relative lowering of vapour pressure for a dilute solution.
Answer:
Relative lowering vapour pressure and molality are related by the equaton:
where,
m = molality of the solution
MA = Molar mass of the solvent.
Define osmatic pressure.
Answer:
Osmotic pressure is the minimum pressurewhich needs to be applied to a solution to prevent the inward flow of water across a semipermeable membrane. It is also definedas the measure of the tendency of a solution to take in water by osmosis.
or
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:
Π = C R T
Here Π is the osmotic pressure and R is the
gas constant.
State Raoult’s layer for a binary solution containing volatile components.
Answer:
Raoult's law states that for a solution of volatile liquid, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
Thus if there is solution of two liquid component 1and 2, then
for component 1,
Where
p1p2 = partial vapour pressure of two volatile component in solution 1 and 2
= vapour pressure of pure component1 and 2
x1x2 = mole fraction of component.
Two liquids A and B boil at 1450C and 1900C respectively. Which of them has higher vapour pressure at 900C.
Answer:
Lower A has lower boiling point so it is being more volatile and has high vapour pressure at 800 C. Becausevapour pressure has an inverse relation with boiling point.
Of 0.1 molal solutions of glucose and NaCl respectively which one will have a higher boiling point?
Answer:
In the same volume of water,0.1 molar of NaCl will have a greater boiling point elevation, as boiling point elevation is a colligative property which depends on the relative amount of the constituent and not on their identity.
Since more ions will be produced by NaCl (ionic compound) than glucose (covalent compound)
as there are more componets part in the NaCl molecule so the NaCl will have more boiling point.
Give reason when 30 ml of ethyl alcohol an 30 ml of water are mixed, the volume of resulting solution is more than 60 ml.
Answer:
It is because ethyl alchol and water do not form an ideal solution the intermolecular forces of attraction are weak so the molecules will become far apart from each other hence volume wll increase.
Draw a suitable labelled diagram to express the relationships for ideal solutions of A and B between vapour pressures and mole-fractions of components at constant temperature.
Answer:
(i) The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e.,
ΔmixH = 0
ΔmixV = 0
It means that no heat is absorbed or evolved when the components are mixed. Also, the volume of solution would be equal to the sum of
volumes of the two components.
(ii)
At molecular level, ideal behaviour of
the solutions can be explained by considering two components A and B. In pure components, the intermolecular attractive interactions will
be of types A-A and B-B, whereas in the binary solutions in addition to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal
solution.
example: Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, etc.
Escaping tendency of 'A' and 'B' should be same in pure liquids and in the solution.
Show graphically that freezing point of a liquid will be depressed when a non-volatile solute is dissolved in it.
Answer:
when a non-volatile solid is added to the solvent
its vapour pressure decreases and now it would
become equal to that of solid solvent at lower
temperature. Thus, the freezing point of the
solvent decreases
Give one example each of miscible liquid pairs showing positive and negative deviations from Raoult’s law. Give one reason for such deviations.
Answer:
Positive deviation from a Raoult's law:
mixture of ethanol and cyclohexane show positive deviation.
when pure ethanol is added to cyclohexane the moleculeof cyclohexane come in between the molecule of ethanol which result in the breaking of hydrogen bond and thus positive deviation.
Negative deviation from Raoult's law:
Mixture of chloroform and acetone shows negtive deviation when these are mixed hydrogen bond is formed and negtive deviation is shown:
State Raoult’s law for solutions where only solvent is volatile. Derive a mathematical exression for this law.
Answer:
Raoult's law states that for a solution of volatile liquid, the partial vapour pressure of each component in the solution is dirctly proportional to its mole fraction.
Thus if there is solution of two liquid component 1 and 2 then,
for component 1,
State with a suitable diagram and appropriate examples why some non-ideal solutions. Show positive deviation from ideal behavour.
Answer:
In case of negative deviations from Raoult’s law, the intermolecular attractive forces between A-A and B-B are weaker than those between A-B and leads to decrease in vapour pressure resulting in negative
deviations. An example of this type is a mixture of phenol and aniline.
In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the respective intermolecular hydrogen bonding between similar
molecules.
This decreases the escaping tendency of molecules for each component and consequently the vapour pressure decreases resulting
in negative deviation from Raoult’s law
What is meant by abnormal mass of solute? Discuss the factors which bring abnormality in the experimentally determined molecular masses of solutes using colligative properties.
Answer:
A molar mass that is either lower or higher than the expected or normal value is called as abnormal molar mass.
In order to account for all such abnormalities, introduced a factor
(i) known as van 't Hoff's factor, which represents the extent of association (or) dissociation of a solute.
Van't Hoff's factor is defined as the ratio of the observed colligative property to the calculated colligative property.
i = Observed colligative property / Calculated colligative property
Observed colligative property ∝ 1/Molar Mass
i = Mc/Mo
Van't Hoff's factor
(i) represents the extent of association (or) dissociation of a solute
i = Total number of moles of particles after association or dissociation / Number of moles of particles before association or disscussion
Experimentally determined molar mass is always lower than actual value for dissociation.
Molar Mass ∝ 1/Colligative Property
If the solute undergoes association in a solution, then the value of van 't Hoff's factor is less than one. If the solute undergoes dissociation then 'i' is greater than one.
Ex:
KCl → K+ + Cl-
1 molecule of KCl furnishes 2 ions in solution
i = Total number of moles of particles after dissociation / Number of moles of particles before dissociation
i = 2/1 = 2
2CH3COOH ⇔(CH3COOH)2
Ethanoic acid Dimer of Ethanoic acid
i = Total number of moles of particles after association / Number of moles of particles before association
i = 1/2 = 0.5
State the type of non-ideality exhibited by a solution of cyclohexane and ethanol or a solution of acetone and chloroform (only one case). Give reason for your answer.
Answer:
The solution of ethanol and cyclohexane show positive deviation.
this is because when pure ethanol is added to cyclohexane the molecule of cyclohexane come in between the molecule of ethanol which result in the breaking f hydrogen bond and thus positive deviation .
another case can be
the mixture of chloroform and acetone shows negtive deviation.
When these are mixed , hydrogen bond is formed and negtive deviation shown;
Miscible liquid pairs often show negative or positive deviation from Raoult’s law. What is the reason for such deviations? Give one example of each type of liquid pairs.
Answer:
When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution.
The vapour pressure of such solution either be higher or lower. i.e positive when higher
negtive when lower.
The cause for these deviations lie in the nature of interactions at the molecular level.
In case of positive deviation from Raoult’s law,
A-B interactions are weaker than those between A-A or B-B, i.e., in this case the intermolecular attractive forces between the solute-solvent molecules are weaker than those between the solute-solute and solvent-solvent molecules. This means that in such solutions, molecules of A (or B) will find it easier to escape than in pure state. This will increase the vapour pressure and result in positive deviation. Mixtures of ethanol and acetone behave in this manner.
In case of negative deviations from Raoult’s law, the intermolecular attractive forces between A-A and B-B are weaker than those between
A-B and leads to decrease in vapour pressure resulting in negative deviations. An example of this type is a mixture of phenol and aniline.
In this case the intermolecular hydrogen bonding between phenolic proton and lone pair on nitrogen atom of aniline is stronger than the
respective intermolecular hydrogen bonding between similar molecules.
Define vapour pressure of a liquid. What happens to the vapour pressure when (a) a volatile solute dissolves in the liquid and (b) non-volatile solute dissolvedin it?
Answer:
Liquids at a given temperature vapourise and under
equilibrium conditions the pressure exerted by the vapours of the liquid over the liquid phase is called vapour pressure.
When a volatile solute is dissolved into, solvent then the vapour state solute and the solvent.
total vapour pressure above such a solution will be equal to the sum of the pressure exerted by the vapours of both solute and solvent.
Where
Ptotal = total pressure of solution
(b)
When a non- volatile solute is dissovled then there is lowering in vapour pressure .
The lowering in vapour pressureisgiven by
Show graphically how the vapour pressure of a solvent and a solution in it of a non-volatile solute change with temperature. Show on this graph the boiling points of the solvent and the solution. Which is higher and why?
Answer:
Elevation of boiling point with addition of non-volatile solute vapour pressure decrese and hence boiling point increase.
Let be the boiling point of pure solvent and
Tb be the boiling point of solution. The increase in
the boiling point is known as
elevation of boiling point.
for dilute
solutions the elevation of boiling point (ΔTb) is
directly proportional to the molal concentration of
the solute in a solution. Thus
ΔTb ∝ m
or
ΔTb = Kb m
Here m (molality) is the number of moles of solute dissolved in 1 kg of solvent and the constant of proportionality, Kb is called Boiling Point Elevation Constant or Molal Elevation Constant. The unit of Kb is K kg mol-1.If w2 gram of solute of molar mass M2 is dissolved in w1 gram of solvent, then molality, m of the solution is given by the expression:
Thus, in order to determine M2, molar mass of the solute, known mass of solute in a known mass of the solvent is taken and ΔTb is
determined experimentally for a known solvent whose Kb value is known.
An antifreeze solution is prepared from 222.6 g of ethylene glycol (C2H4(OH)2) and 200 g of water. Calculate the molality of the solution. If the density of this solution be 1.072 g ml–1, what will be the molarity of the solution?
Molecular mass of glycol C2H4(OH)2 =62
= mass of glycol / molar mass of glycol
= 222.6/62=3.59 moles
Molality of solution =
number of moles of solute / mass of solvent in Kg
Mass of solvent = 200g = 200/1000 Kg = 0.2 kg
Plug the values we get
Molality = 3.59/0.2
Molality = 17.95
Formula of molarity of solution = number of moles of solute / volume of solution in Kg
Molarity =9.1M
At 300 K, 36 g of glucose (C6H12O6) present per litre in its aqueous solution has an osmotic pressure of 4.98 bar. If the osmotic pressure of another solution of glucose is 1.52 bar at the same temperature, what would be its concentration?
Answer:
Let us calculate the concentration of the first solution with osmatic pressure 4.98bar
mass of glucose = 36g
molar mass of gulcose = 180g/ mol
therefore number of moles of gulcose = 36/180
= 0.2 moles
volume of the solution = 1L
molarity = No. of moles of glucose / vol.of solution
molarity =0.2/1L
C1 = 0.2 moles/L
A 0.1539 molal aqueous solution of cane sugar (mol. mass = 342 g mol–1) has a freezing point of 271 K while the freezing point of pure water is 273.15 K. What will be the freezing point of an aqueous solution containing 5 g of gluocose (mol. mass = 180 g mol–1) per 100 g of solution?
Answer:
The molality of the cane sugar, m= 0.1539m
depression in freezing point = 273.15-271
=2.15K
Since = Kfm
or Kf = /m = 2.15k/0.1539m = 13.97K/m
Now the weight of glucose , W2 = 5g
molecular mass of glucose, M2 =180g/mol
then =Kfm
=
then freezing point of solution = 273.15-3.88
=263.27K
The vapour pressure of water is 12.3 kPa at 300 K. Calculate the vapour pressure of a one molal solution of a non-volatile, non-ionic solute in water.
P=P(pure)X ...........1
Here we know the value of P(pure)so need to find the value of molar fraction X
Why is the vapour pressure of a solution of glucose in water lower than that of water?
Answer:
The vapour pressure of a pure solvent decrease .
when a non-volatile solute is added to the solvent
this is because on adding the solute a fewer number of water molecules are present at the surface which can evaporate as some of the area is occupied by -non- volatile solute molecules thereby decreasing the vapour pressure of the solution of the glucose in wateris lower than pure water.
A 6.90 M solution of KOH in water contains 30% by mass of KOH. Calculate the density of the KOH solution. [Molar mass of KOH = 56 g mol–1]
Answer;
Let the density of solution = d g/cm3
and volume of solution is = 1L = 1000 cm3
mass of the solution = d xV
= (1000d)g
6.90 M solution mean 1L solution contains 6.90 moles of KOH
therefore mass of KOH = 6.90 x 56 = 386.4g
but only 30% of the solutionby mass is KOH
therefore
30/100 x (1000)d =386.4
and density is 1.288g/ cm3
Give reasons for the following:
When 30 ml of ethyl alcohol and 30 ml of water are mixed, the volume of resulting solution is more than 60 ml.
Answer:
When 30 ml of ethyl alcohol and 30 ml of water are mixed, the volume of resulting solution is more than 60ml.
It is because ethyl alchol and water do not form an ideal solution intermolecular forces of attraction are weak so the molecule will become farapart from each other hence volume will increase.
Give reasons for the following:
Copper is conducting as such while copper sulphate is conducting only in molten state or in aqueous solution.
Answer:
Copper sulphate conduct electricity only in molten state or in aqueous phase because on dissolving or melting it. copper sulphate dissociate in copper ion and sulphate ion and became free to move.
As they are freeto move in molten and aqueous phase the charge particle conduct electricity.
In solid and any other ionic form the ions held in a lattice and unable to move so they are not conduct electricity.
Urea forms an ideal solution in water. Determine the vapour pressure of an aqueous solution containing 10% by mass of urea at 400C. (Vapour pressure of water at 400C = 55.3 mm of Hg)
Answer:
by using formula .
let the mass of solution be 100g
therefore mass of urea = 10g
molecular mass of urea = 60 g
xurea = 10/60 = 1/6
molecular mass of water = 18 g
xwater = 90/18 = 5
mole fraction of urea =
Why is freezing point depression of 0.1 M sodium chloride solution nearly twice that of 0.1 M glucose solution?
Answer:
0.1M NaCl and0.1M glucose solution means that 0.1 moles of solute dissolve in 1L of solvent.
weight of solvent in both solution is same .
Dpression in freezing point can br calculated as :
Where
Kf = molal depression constant
wB = weight of solute
wA= weight of solvent
MB = molar mass of the solute
mass of NaCl = 58.69g/mol
mass of glucose = 180g/mol
The depression in freezingpoint is inversly proprotional to molar mass of solute thus more is molar mass of solute lesser is the depression in freezing point .
Thus it can explain that the NaCl wil be more than the glucose.
A 6.90 M solution of KOH in water contains 30% by mass of KOH. Calculate the density of the KOH solution. (Molar mass of KOH = 56 g mol–1)
Answer;
Let the mass of solution =100g
xKOH = 30/56
volumeof solution =
Urea forms an ideal solution in water. Determine the vapour pressure of an aqueous solution contains 10% by mass of urea at 400C. (Vapour pressure of water at 400C = 55.3 mm of Hg)
Answer:
= xurea
Let the mass of solution be 100g
therefore mass of urea = 10 g
molecular mass of urea = 60 g
xurea = 10/60 =1/6
molecular mass of water = 18g
xwater = 90/18 =5
A solution is made by dissolving 30 g of a non-volatile solute in 90g of water. It has a vapour pressure of 2.8 kPa at 298 K. At 298 K, vapour pressure of pure water is 3.64 kPa. Calculate the molar mass of the solute.
The relative lowering of vapour pressure is given by the following expression.
Where is the vapour pressure of pure solvent, Psolution is the vapour pressure of solution containing dissolved solute, n1 is the number of moles of solvent and n2 is the number of moles of solute.
For dilute solution n2<<n1, therefore the above expression reduces to
Where w1 and w2 are the masses and M1 and M2 are the molar masses of solvent and solute respectively.
We are given that
W1 =30 g
W2 =30g
psolution =2.8 kpa
p0solvent =? And M2=?
At 300 K, 36 g of glucose present per litre in its solution has an osmotic pressure of 4.98 bar. If osmotic pressure of solution is 1.52 bar at the same temperature, what would be its concentration.
Answer:
=
C = 0.061 M
Calculate the vapour- pressure lowering of water when5.67g of glucose, C6H12O6 is dissolved in 25.2 g water at 250C. The vapour pressure of water at 250C is 23.8 mmHg. What is the vapour pressure of the solution?
WB =5.67g
WA =25.2g
MB=180g/mol
MA=18g/mol
NB= 5.67/180 =0.0315 mol glucose
NA=25.2/18 =1.40 mol water
A 4% solution of sucrose is isotonic with 3% solution of an unknown organic substance. Calculate the molecular mass of unknown resistance.
Answer:
AS both the solution are isotonic they should have same concentrationin mole/litre
for sucrose solution concentration =4g/100cm3
= 40g/Litre
molar mass of sucrose C 12H22O11 = 342
therefore we get =40/342 moles/litre
For unknown substance Let N be the molecular mass then concentration = 3g/100cm3
= 30g/Litre
= 30/N moles/Litre
comparing the both equation
30/N = 40/342
N=(30 x 342)/40
N= 256.5
Molecular mass of oragnic compound
Calculate molarity and molality of 13% solution (by weight of sulphuric acid. Its density is 1.020 g cm–3. (At. mass, H = 1,16, S = 32 amu).
Answer:
13 % of solution of sulphuric acid contains 13 g of H2SO4in 100 g of the solution. Weight of water = 100 - 13 = 87 g.
mole of H2SO4 = 13/98 mole
Volume of H2SO4 solution + Weight of soluton / Density = 100/1.02 ml
= 100 / 1.02 x 1/1000 = 1/1.02 litre
Molarity of H2SO4 solution = mole of H2SO4 / Volume of solution
= 13/98 / 1/1.02 = 10.2 x 13/98 = 1.353 M
Molality of H2SO4 solution = mole of H2SO4 / wt of water in kg. = 13/98 / 87/1000 = 13/98 x 1000/87
= 1.525 mol kg-1 (mole Kg-1)
What is osmotic pressure? How would you determine the molecular mass of solute with the help of osmotic pressure?
Answer:
osmotic pressure is proportional to the molarity, C of the solution at a given temperature T. Thus:
Π = C R T
Here Π is the osmotic pressure and R is the
gas constant.
Π = (n2 /V) R T
Here V is volume of a solution in litres containing n2 moles of solute.
If w2 grams of solute, of molar mass, M2 is present in the solution, then
n2 = w2 / M2 and we can write,
Thus, knowing the quantities w2, T, Π and V we can calculate the molar mass of the solute.
Explain with a suitable diagram and appropriate examples. Why some non-ideal solutions show positive deviation from ideal behavour?
Answer:
In case of positive deviation from Raoult’s law, A-B
interactions are weaker than those between A-A or B-B, i.e., in this case the intermolecular attractive forces between the solute-solvent molecules
are weaker than those between the solute-solute and solvent-solvent molecules. This means that in such solutions, molecules of A (or B) will
find it easier to escape than in pure state. This will increase the vapour pressure and result in positive deviation. Mixtures of ethanol and acetone is good example of this.
Derive an expression relating the elevation of boiling point to the amount of solute present in the solution.
Answer:
the vapour pressure of a liquid increases with increase of temperature. It boils at the temperature at which its vapour pressure is equal to the atmospheric pressure. For example, water boils at 373.15 K (100° C) because at this temperature the vapour pressure of water is 1.013 bar (1 atmosphere)
Let be the boiling point of pure solvent and
Tb be the boiling point of solution. The increase in
the boiling point is known as
elevation of boiling point.
for dilute solutions the elevation of boiling point (ΔTb) is directly proportional to the molal concentration of the solute in a solution. Thus
ΔTb ∝ m
or ΔTb = Kb m
Here m (molality) is the number of moles of solute dissolved in 1 kg of solvent and the constant of proportionality, Kb is called Boiling Point Elevation Constant or Molal Elevation Constant (EbullioscopicConstant). The unit of Kb is K kg mol-1. If w2 gram of solute of molar mass M2 is dissolved in w1 gram of solvent, then molality, m of the solution is given by the expression:
Thus, in order to determine M2, molar mass of the solute, known mass of solute in a known mass of the solvent is taken and ΔTb is
determined experimentally for a known solvent whose Kb value is known.
Derive an expression relating the depression of freezing point with the amount of solute present in the solution.
Answer:
the freezing point of a substance may be defined as the temperature at which the vapour pressure of the substance in its liquid phase is equal to its vapour pressure in the solid phase.
According to Raoult’s law, when a non-volatile solid is added to the solvent its vapour pressure decreases and now it would become equal to that of solid solvent at lower temperature. Thus, the freezing point of the solvent decreases.
Let be the freezing point of pure solvent and Tf be its freezing point when non-volatile solute is dissolved in it. The decrease in freezing point.
Similar to elevation of boiling point, depression of freezing point (ΔTf) for dilute solution (ideal solution) is directly proportional to molality,
m of the solution. Thus,
ΔTf ∝ m
or
ΔTf= Kfm
The proportionality constant, Kf, which depends on the nature of the solvent is known as Freezing Point Depression Constant or Molal Depression Constant or Cryoscopic Constant. The unit of Kf is K kg mol-1
If w2 gram of the solute having molar mass as M2, present in w1 gram of solvent, produces the depression in freezing point ΔTf of the
solvent then molality of the solute is given by the equation:
Thus for determining the molar mass of the solute we should know the quantities w1, w2, ΔTf, along with the molal freezing point depression constant.
State and explain Raoult’s law. How would you distinguish between an ideal and non-ideal solution?
Answer:
Raoult's law state that for any solution the partial vapour pressure of each volatile component in the solution is directly proportional to its mole fraction.
p1 ∝ x1
and p1 = x1
The proportionality constant is equal to the vapour pressure of pure solvent, .
IDEAL SOLUTION
(i) The solutions which obey Raoult’s law over the entire range of concentration are known as ideal solutions. The ideal solutions have two other important properties. The enthalpy of mixing of the pure components to form the solution is zero and the volume of mixing is also zero, i.e.,
ΔmixH = 0
ΔmixV = 0
It means that no heat is absorbed or evolved when the components are mixed. Also, the volume of solution would be equal to the sum of
volumes of the two components.
(ii)
At molecular level, ideal behaviour of
the solutions can be explained by considering two components A and B. In pure components, the intermolecular attractive interactions will
be of types A-A and B-B, whereas in the binary solutions in addition to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are nearly equal to those between A-B, this leads to the formation of ideal
solution.
example: Solution of n-hexane and n-heptane, bromoethane and chloroethane, benzene and toluene, etc.
NON-IDEAL SOLUTION
When a solution does not obey Raoult’s law over the entire range of concentration, then it is called non-ideal solution.
In non-ideal solution the vapour pressure of such a solution is either higher or lower than that predicted by Raoult’s law, If it is higher, the solution exhibits positive deviation and if it is lower, it exhibits negative deviation.
IN case of non-ideal solution
ΔmixH ,ΔmixV
both are not equal to zero. it either be less than zero or greater than zero.
IN case of positive deviation it be larger and In case of negtive deviation it be lesser.
in the binary solutions in addition to these two interactions, A-B type of interactions will also be present.
If the intermolecular attractive forces between the A-A and B-B are not nearly equal to those between A-B, this leads to the formation of non ideal solution.
example :a mixture of chloroform and acetone etc.
What is meant by positive deviations from Raoult's law? Give an example. What is the sign of mixH for positive deviation?
OR
Define azeotropes. What type of azeotrope is formed by positive deviation from Raoult's law? Give an example.
The solutions that do not obey Raoult’s law over the entire range of concentration are known as non-ideal solutions. They have vapour pressures either higher or lower than those predicted by Raoult’s law. If the vapour pressure is higher, then the solution is said to exhibit a positive deviation from Raoult’s law.
A mixture of ethanol and acetone is an example of a solution that shows a positive deviation from Raoult’s law.
In case of solutions showing positive deviations, absorption of heat takes place that mixH has a positive sign.
OR
Azeotropes are the binary mixtures of solutions that have the same composition in liquid and vapour phases and that have constant boiling points.
A minimum-boiling azeotrope is formed by solutions showing a large positive deviation from Raoult’s law at a specific composition.
Example: An ethanol–water mixture containing approximately 95% ethanol by volume
3.9 g of benzoic acid dissolved in 49 g of benzene shows a depression in freezing point of 1.62 K. Calculate the van't Hoff factor and predict the nature of solute (associated or dissociated).
(Given: Molar mass of benzoic acid = 122 g mol-1, Kf for benzene = 4.9 K kg mol-1
We know that the depression in freezing point is given by
![]()
Here
Depression in freezing point K
Kf for benzene=4.9kg mol-1
Mass of benzene W=49g
Molar mass of benzoic acid ms = 122g mol-1
Substituting the value we get
1.62 = 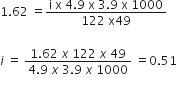
As the value of i<1 benzoic acid is associated solute.
Calculate the mass of compound (molar mass = 256 g mol-1) to be dissolved in 75 of benzene to lower its freezing point by 0.48 K (Kf= 5.12 kg mol-1 )
We have given:
Tf = 0.48 K
Kf=5.12K kg mol-1
W1 = 75 g
W2 = ?
M2 = 256 g mol-1
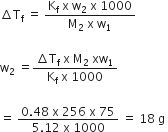
Define an ideal solution and write one of its characteristics.
Definition: The solutions that obey Raoult’ s law over the entire range of concentration are called ideal solutions. Examples: n-hexane and n-heptane.
Characteristics: For ideal solutions:
Enthalpy of mixing (mixH) of the pure components to form the solution is zero.
The volume of mixing (mixV) is also equal to zero.
18 g of glucose, C6H12O6 (Molar Mass = 180 g mol-1) is dissolved in 1 kg of water in a saucepan. At what temperature will this solution boil?
(Kb for water = 0.52 K kg mol-1, boiling point of pure water = 373.15 K)
w1 = weight of solvent (H2O) = 1 kg
w2 = weight of solute (C6H12O6) = 18 gm
M2 = Molar mass of solute (C6 H12O6) = 180 g mol-1
Kb = 0.52 K Kg mol-1

Determine the osmotic pressure of a solution prepared by dissolving 2.5 x 10-2 g of K2SO4 in 2L of water at 250C, assuming that it is completely dissociated.
(R = 0.0821 L atm K-1 mol-1, Molar mass of K2SO4 = 174 g mol-1)
w2 = 2.5 x 10-2 g (Mass of K2SO4)
M2 = 174 g mol-1 (Molar mass of K2SO4)
V = 2L,
R = 0.0821 L atm K-1 mol-1 and
T = 25°C = 298 K
Osmotic pressure,
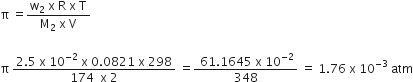
A 1.00 molar aqueous solution of trichloroacetic acid (CCl3COOH) is heated to its boiling point. The solution has the boiling point of 100.180C. Determine the van’t Hoff factor for trichloroacetic acid. (Kb for water = 0.512 kg mol-1)
Molality of solution = m = 1.00 m
Boiling points of solution = Tb = 100.180C = 373.18 K
Boiling point of water (solvent) =  = 100.00° C = 373 K
= 100.00° C = 373 K
Elevation in boiling point =  - Tb
- Tb
Observed boiling point = 373.18 K - 373 K = 0.18 K
Kb water = 0.512 K kg mol- 1
∴  T b= Kb x m
T b= Kb x m
= 0.512 x 1 = 0.512 K
∴ Calculated boiling point = 0.512 K
Define the following terms:
(i) Mole fraction
(ii) Isotonic solutions
(iii) Van’t Hoff factor
(iv) Ideal solution
(i) Mole fraction: The mole fraction of a component in a mixture is defined as the ratio of the number of moles of the component to the total number of moles of all the components in the mixture. Mathematically, it is represented as:
![]()
Mole fraction is denoted by ‘x’.
(ii) Isotonic solution: It is a type of solution that has the same salt concentration as its surrounding environment and thus the substances around it neither lose nor gain water by osmosis.
(iii) Van’t Hoff factor: It is defined as the ratio of the experimental value of colligative property to the calculated value of the colligative property and is used to find out the extent of dissociation or association.
Mathematically, it is represented as:

For association, i < 1
For dissociation, i > 1
No association or dissociation, i = 1
Examples: One formula unit of NaCl will create two particles in solution, a Na+ ion and a Cl- ion.
One formula unit of CaCl2 will create three particles in solution, a Ca+ ion and two Cl- ions.
(iv) Ideal Solutions: Ideal Solutions are those which obey Raoult's Law at all concentrations and Temperatures. Some examples of ideal solution liquid pairs are benzene and toluene, n-heptane and n-hexane, ethyl bromide and ethyl iodide, chlorobenzene and bromobenzene etc.
(a) Differentiate between molarity and molality for a solution. How does a change in temperature influence their values?
(b) Calculate the freezing point of an aqueous solution containing 10.50 g of MgBr2in 200 g of water. (Molar mass of MgBr2 = 184 g) (Kf for water = 1.86 K kg mol-1)
Molarity is defined as the number of moles of solute dissolved per liter of solution.
![]()
Molality of a solution is defined as the number of moles of solute dissolved in 1000 grams of solvent.
![]()
While molarity decreases with an increase in temperature, molality is independent of temperature. This happens because molality involves mass, which does not change with a change in temperature, while molarity involves volume, which is temperature dependent.
b) Given
w2 = 10.50 g
w1 = 200 g
Molar mass of MgBr2 (M2) = 184 g
Using the formula,
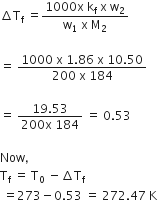
(a) Define the terms osmosis and osmotic pressure. Is the osmotic pressure of a solution a colligative property? Explain.
(b) Calculate the boiling point of a solution prepared by adding 15.00 g of NaCl to 250.0 g of water. (Kb for water = 0.512 K kg mol-1), (Molar mass of NaCl = 58.44 g)
(a) Osmosis: The process of flow of solvent molecules from pure solvent to a solution or from a solution of lower concentration to a solution of higher concentration through a semi-permeable membrane is called osmosis.
Osmotic Pressure: The pressure required to just stop the flow of solvent due to osmosis is called osmotic pressure (π) of the solution.
Yes, the osmotic pressure of a solution is a colligative property. The osmotic pressure is expressed as.
![]()
Where,
π = osmotic pressure
n = number of moles of solute
V = volume of solution
T = temperature
From the equation, it is clear that osmotic pressure depends on upon the number of moles of solute ‘n’ irrespective of the nature of the solute.
Hence, osmotic pressure is a colligative property.
(b) Given
Kb = 0.512 k kg mol-1
w2 = 15.00 g
w1 = 250.0 g
M2 = 58.44 g
Using the formula,

Why does a solution containing non-volatile solute have higher boiling point than the pure solvent? Why is elevation of boiling point a colligative property?
The boiling point of substance can be defined as, it is the temperature at which the vapour pressure of the substance equal to atmospheric pressure. According to Raoult's law, the vapour pressure of a solvent decreases in the presence of a non-volatile solute. Thus, the vapour pressure of a solution containing a non-volatile solute requires a high temperature to become equal to the atmospheric pressure. That is why the boiling point of a solution containing a non-volatile solute increases. Thus, the solution containing a non-volatile solute has a higher boiling point than a pure solvent. Example of non-volatile solute sugar, NaCl. etc.
Elevation in boiling point is a colligative property, as it depends on the number of solute particles present in a solution.
Calculate the freezing point of the solution when 31 g of ethylene glycol (C2H6O2) is dissolved in 500 g of water. (Kf for water = 1.86 K kg mol–1)
The freezing point of pure water is 273.15 K. On dissolving ethylene glycol, freezing point, being a colligative property, will be lowered.
![]()
We are given that
Kf for water =1.86 K kg mol-1
Mass of solute, ws = 37 g
Molar mass of solute, Ms = 12 x 2 + 1 x 6 + 16 x 2
= 62 g mol-1
Mass of water, W = 500 g
Therefore ![]()
Hence, the freezing point of the solution, Tf = 273.15K – 1.86 K
= 271.29 K
(a) State Raoult’s law for a solution containing volatile components.
How does Raoult’s law become a special case of Henry’s law?
(b) 1·00 g of a non-electrolyte solute dissolved in 50 g of benzene lowered the freezing point of benzene by 0·40 K. Find the molar mass of the solute. (Kf for benzene = 5·12 K kg mol-1)
(a) Let p1, p2 = Partial vapour pressure of two volatile components 1 and 2 of a mixture ![]()
= Vapour pressure of pure components 1 and 2
x1, x2 = Mole fractions of the components 1 and 2
ptotal = Total vapour pressure of the mixture then Raoult’s law can be stated as: For a solution of volatile liquids, the partial vapour pressure of each component in the solution is directly proportional to its mole fraction.
That is, for component 1,
p1 ![]() x1
x1
And, p1 = ![]() x1
x1
For component 2,
P2 = ![]() x2
x2
According to Dalton’s law of partial pressures,
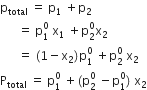
The plot of vapour pressure and mole fraction of an ideal solution at constant temperature is shown below.
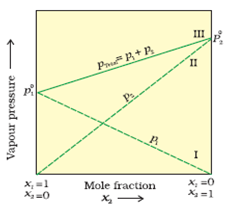
Raoult’s Law as a Special Case of Henry’s Law
According to Raoult’s law, the vapour pressure of a volatile component in a given solution is p1 = ![]() x1
x1
According to Henry’s law, the partial vapour pressure of a gas (the component is so volatile that it exists as gas) in a liquid is
p = KH x
It can be observed that in both the equations, the partial vapour pressure of the volatile component varies directly with its mole fraction. Only the proportionality constants KH and are different. Thus, Raoult’s law becomes a special case of Henry’s law in which KH is equal to .
(b) Given: w2 = 1g (weight of solute)
w1 = 50 g (weight of solvent)
Tf = 0.40 K
kf = 5.12 K Kg mol-1
M2 =? (Molar mass of solute)
Using the equation,
Tf = Kfm (where m is molality)
0.40 = 5.12 x m
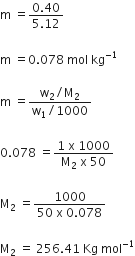
(a) Define the following terms:
(i) Ideal solution
(ii) Azeotrope
(iii) Osmotic pressure
(b) A solution of glucose (C6H12O6) in water is labeled as 10% by weight. What would be the molality of the solution?
(Molar mass of glucose = 180 g mol-1)
(a)
(i) Ideal Solution:
Solutions which obey Raoult’s law over the entire range of concentrations are known as the ideal solution. Along with that for ideal solution:
Enthalpy of mixing of the pure components to form the solution i.e  mix H = 0 and volume of mixing,
mix H = 0 and volume of mixing,  mix V = 0.
mix V = 0.
An ideal solution will be formed when intermolecular forces of attraction between the molecules of solute (A - A) and those between the molecules of solvent (B -B) are nearly equal to those between solute and solvent molecules (A - B).
For Example n-Hexane and n-heptane
(ii) Azeotropes
Binary mixtures which have the same composition in liquid and vapour phase, and have constant boiling points are known as azeotropes. It is not possible to separate its components by fractional distillation .There are two types of azeotropes:
Minimum boiling azeotrope, example: Ethanol-water mixture containing ethanol approximately 95% by volume.
Maximum boiling azeotrope, example: Nitric acid-water mixture containing 68% nitric acid and 32% water by mass.
(iii) Osmotic Pressure
The process of flow of solvent molecules from pure solvent to a solution or from a solution of lower concentration to a solution of higher concentration through a semi-permeable membrane is called osmosis. The pressure required to prevent the flow of solvent due to osmosis is called osmotic pressure (Ï€) of the solution.
Osmotic pressure is directly proportional to the molarity C of the solution at a given temperature T.
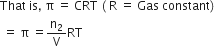
Where,
n2 = Number of moles of solute
V= Volume of the solution in litres
(b) Assume that 100 g of solution contains 10 g of glucose and 90 g of water as our glucose solution is 10% by weight
Where w2 = weight is solute in 'g'
w1 = weight of solvent in 'g'
M2 = Molecular mass of solute.
So,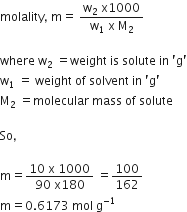
a) Define the following terms:
(i) Mole fraction
(ii) Ideal solution
(b) 15.0 g of an unknown molecular material is dissolved in 450 g of water. The resulting solution freezes at - 0.34°C. What is the molar mass of the material? (Kf for water = 1.86 K kg mol-1)
(i) Mole fraction: The mole fraction of a component in a mixture is defined as the ratio of the number of moles of the component to the total number of moles of all the components in the mixture. Mathematically, it is represented as:
![]()
Mole fraction is denoted by ‘x’.
(ii) Ideal Solution:
Solutions which obey Raoult’s law over the entire range of concentrations are known as ideal solution. Along with that for ideal solution:
Enthalpy of mixing of the pure components to form the solution i.e mix H = 0 and volume of mixing, mix V = 0.
An ideal solution will be formed when intermolecular forces of attraction between the molecules of solute (A - A) and those between the molecules of solvent (B -B) are nearly equal to those between solute and solvent molecules (A - B).
For Example: n-Hexane and n-heptane
(b) Given mass of solute = wb = 15.0g
Molar mass of solute = Mb =?
Mass of water = wa = 450 g
Freezing point of water = 0°C = 273 K
Freezing point of solution = - 0.34°K
= (- 0.34 + 273) K
Depression in freezing point = Tf= 273 - (-0.34 + 273)
= 0.34 K
Kf for water = 1.86 K Kg mol-1
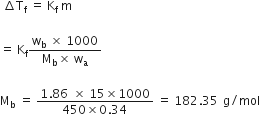
(a) Explain the following:
(i) Henry’s law about the dissolution of a gas in a liquid.
(ii) Boiling point elevation constant for a solvent.
(b) A solution of glycerol (C3H8O3) in water was prepared by dissolving some glycerol in 500 g of water. This solution has a boiling point of 100.42°C. What mass if glycerol was dissolved to make this solution? (Kb for water = 0.512 K kg mol-1)
(a)
(i) Henry’s law states that partial pressure of a gas in the vapour phase is proportional to the mole fraction of the gas in the solution. If p is the partial pressure of the gas in the vapour phase and x is the mole fraction of the gas, then Henry’s law can be expressed as:
p = KHx
Where,
KH is Henry’s law constant
(ii) The boiling point elevation constant or molal elevation constant is a constant quantity for a solute which is related to molar mass and elevation in boiling point by the following relation.
![]()
Where, Kb is the boiling point elevation constant
MB is the molar mass of the solute
WB is the weight of the solute
WA is the weight of the solvent
Tb is the elevation in boiling point
(b) WB =?
WA = 500g
Kb = 0.512 Kkg mol-1
Tb = 100.42°C - 100°C
= 0.42°C
MB = 3 x 12 + 8 x 1 + 3 x 16
= 36 + 8 + 48 = 92
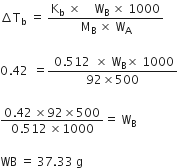
a) Calculate the freezing point of the solution when 1.9 g of MgCl2 (M = 95 g mol−1) was dissolved in 50 g of water, assuming MgCl2 undergoes complete ionization.
(Kf for water = 1.86 K kg mol−1)
(b)
(i) Out of 1 M glucose and 2 M glucose, which one has a higher boiling point and why?
(ii) What happens when the external pressure applied becomes more than the osmotic pressure of solution?
OR
(a)When 2.56 g of sulphur was dissolved in 100 g of CS2, the freezing point lowered by 0.383 K. Calculate the formula of sulphur (Sx).
(Kf for CS2 = 3.83 K kg mol−1, Atomic mass of sulphur = 32 g mol−1]
(b)Blood cells are isotonic with 0.9% sodium chloride solution. What happens if we place blood cells in a solution containing
(i)1.2% sodium chloride solution?
(ii)0.4% sodium chloride solution?
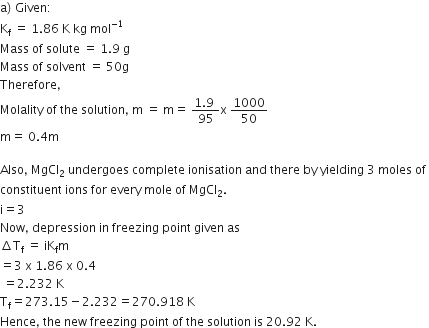
(i) The elevation in the boiling point of a solution is a colligative property; therefore, it is affected by the number of particles of the solute. Since the amount of solute is higher in 2 M glucose solution as compared to 1 M glucose solution, the elevation in the boiling point is higher. Hence, 2 M glucose solution has a higher boiling point than 1 M glucose solution.
(ii) When the external pressure exerted on the solution is higher than the osmotic pressure, the pure solvent starts flowing out of the solution through the semi- permeable membrane. This process is known as reverse-osmosis.
Or

(b)
(i) 1.2% sodium chloride solution is hypertonic wrt 0.9% sodium chloride solution. Therefore, when the blood cells are placed in 1.2% sodium chloride solution, water flows out of the cells and the cells shrink.
(ii) 0.4% sodium chloride solution is hypotonic wrt 0.9% sodium chloride solution. Therefore, when the blood cells are placed in 0.4% sodium chloride solution, water flows into the cells and the cells swell.
(i) Gas (A) is more soluble in water than Gas (B) at the same temperature which one of two gases will the higher value of KH (Henry's constant) and why ?
(ii)In non-ideal solution, what type of deviation shows the formation of maximum boiling azeotropes?
(i)According to Henry's law , at the constant temperature, the solubility of the gas in a liquid is directly proportional to the partial pressure of the gas on the surface of the liquid or solution. Gas B has a Higher value of KH and thus lower is the solubility of the gas.
p = KHx
(ii) Negative deviation from Raoult’s law
What is meant by ‘reverse osmosis’?
The phenomenon of reversal of the direction of osmosis by the application of a pressure larger than the osmotic pressure on the solution side is known as reverse osmosis. In this case, the pure solvent flows out of the solution through a semi-permeable membrane.
Differentiate between molarity and molality values for a solution. What is the effect of change in temperature on molarity and molality values?
Molarity is defined as the number of moles of solute dissolved per litre of solution.
![]()
Molality of a solution is defined as the number of moles of solute dissolved in 1000 grams of solvent.
![]()
A solution prepared by dissolving 8.95 mg of a gene fragment in 35.0 mL of water has an osmotic pressure of 0.335 torr at 25°C.
Assuming that the gene fragment is a non-electrolyte, calculate its molar mass.
The molar concentration of the gene fragment
![]()
Here, WB = 8.95 mg = 8.95 x 10-3 g, R = 0.0821 L atm Mol-1 K-1
T = 250C = (25 + 273) K = 298 K. = 0.355torr =0.355/760 atm
V = 35 mL = 35 x 10-3 L
Substituting these values in the above equation, we get
![]()
(a) Define the following terms :
(i) Molarity
(ii) Molal elevation constant (Kb)
(b) A solution containing 15 g urea (molar mass = 60 g mol–1) per litre of the solution in water has the same osmotic pressure (isotonic) as a solution of glucose (molar mass = 180 g mol–1) in water. Calculate the mass of glucose present in one litre of its solution.
OR
(a) What type of deviation is shown by a mixture of ethanol and acetone? Give reason.
(b) A solution of glucose (molar mass = 180 g mol–1) in water is labelled as 10% (by mass). What would be the molality and molarity of the solution?
(Density of solution = 1.2 g mL–1)
(i) Molarity of a solution is defined as the number of moles of solute present in one litre of the solvent.
(ii) Molal elevation constant (Kb) is defined as the elevation of the boiling point of a solution when one mole of a non-volatile solute is dissolved in one kilogram of a volatile solvent.
(b) Osmotic pressure π = CRT = nVRT/2
where n is the number of moles of solute present in volume V of solvent.
It is given that the solution of urea is isotonic with the solution of glucose, thus
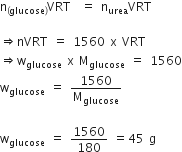
Or
a) A mixture of ethanol and acetone shows positive deviation from Raoult's Law. Pure ethanol possesses hydrogen bonding. The introduction of acetone between the molecules of ethanol results in breaking of some of these hydrogen bonds. Due to the weakening of interactions, the solution shows positive deviation from Raoult’s law.
(b)
10% by mass solution of glucose in water means that 10 g of glucose in present in 100 g of the solution i.e., 10 g of glucose is present in (100 - 10) g = 90 g of water.
Molar mass of glucose (C6H12O6) = 180 g mol-1 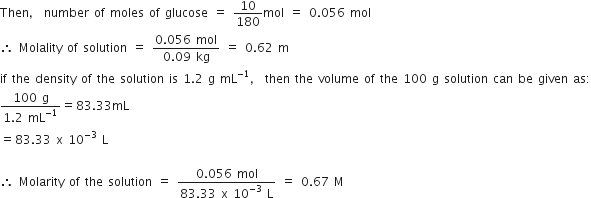
Define the following terms:
Colligative properties
Colligative properties are properties of solutions that depend on the ratio of the number of solute particles to the number of solvent molecules in a solution, and not on the nature of the chemical species present.Colligative properties include vapour pressure lowering, boiling point elevation, freezing point depression, and osmotic pressure.
Define the following terms:
Molality (m)
Molality of a solution is defined as the number of moles of solute dissolved per kg of solvent.
![]()
A 10% solution (by mass) of sucrose in water has the freezing point of 269.15 K.Calculate the freezing point of 10% glucose in water if freezing point of pure water is273.15 K.
Given : (Molar mass of sucrose = 342 g mol–1) (Molar mass of glucose = 180 g mol–1)
Given,
T1=269.15 K
T2 = 273.15
Molar mass of sucrose = 342 g mol–1
Molar mass of glucose = 180 g mol–1
ΔTf = Kf m
Here , m = w2x 1000/ M2XM1
273.15-269.15 = Kf x 10 x1000/ 342 x90
Kf = 12.3 K kg/mol
ΔTf = Kf m
= 12.3 x 10 x1000/ 180x90
= 7.6 K
Tf = 273.15 – 7.6 = 265.55 K
Write one difference in each of the following:
Solution and Colloid
| Solution | Colloid | |
| Appearance | It is clear, transparent and homogeneous | It is Cloudy but uniform and homogeneous |
| Tyndall effect | solution does not show Tyndall effect | colloid Shows Tyndall effect |
Calculate the freezing point of a solution containing 60 g of glucose (Molar mass = 180 g mol–1) in 250 g of water.
(Kf of water = 1.86 K kg mol–1)
We know,
W1 = 250 g, w2 = 60 g, mw2 = 180 g/mol, Kf = 1.86 k kg mol–1
Give reasons for the following :
Measurement of osmotic pressure method is preferred for the determination of molar masses of macromolecules such as proteins and polymers.
Protein is the high molecular mass material the magnitude of colligative property depends inversely on the molecular mass and osmotic pressure.
Osmotic pressure is fine at room temp, no special arrangements are required and it depends on molarity whereas all other colligative properties depend on molality.
Give reasons for the following:
Aquatic animals are more comfortable in the cold water than in warm water.
The solubility of oxygen decreases as temperature rises which means solubility of oxygen in warm water is less as compared to cold water. Hence, aquatic animals are more comfortable in the cold water.
Give reasons for the following:
Elevation of the boiling point of 1 M KCl solution is nearly double than that of 1 M sugar solution.
The elevation of boiling point is Δtb = iKbm in both 1M KCl & 1 M sugar. As colligative property depends only on a number of particle and KCl as electrolyte will produce a double number of a particle of sugar. Hence the value van’t hoff factor is twice in 1m KCl then 1M sugar due to which elevation in boiling point is more.
18 g glucose (C6H12O6 ) is added to 178.2 g water. The vapor pressure of water (in torr) for this aqueous solution is:
-
76.0
-
752.4
-
759.0
-
7.6
B.
752.4
Vapour pressure of water (p°) = 760 torr
Number of moles of glucose
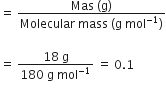
Molar mass of water = 18 g/mol
Mass of water (given) = 178.2 g
Number of moles of water
![]()
Total number of moles = (0.1 +9.9) = 10 moles
Now, the mole fraction of glucose in solution = Change in pressure with respect to initial pressure.
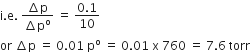
therefore, Vapour pressure of solution = (760-7.6)torr
=752.4 torr
The vapour pressure of acetone at 20oC is 185 torr. When 1.2 g of a non-volatile substance was dissolved in 100 g of acetone at 20oC, its vapour pressure was 183 torr. The molar mass (g mol-1 ) of the substance is:
-
32
-
64
-
128
-
488
B.
64
Given,
po = 185 torr at 20oC
ps = 183 torr at 20oC
Mass of non-volatile substance,
m= 1.2 g
Mass of acetone taken = 100 g
As we have, ![]()
putting the values, we get
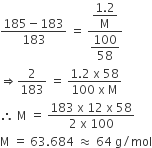
3 g of activated charcoal was added to 50 mL of acetic acid solution (0.06N) in a flask. After an hour it was filtered and the strength of the filtrate was found to be 0.042 N. The amount of acetic acid adsorbed (per gram of charcoal) is:
-
18 mg
-
36 mg
-
42 mg
-
54 mg
A.
18 mg
The initial strength of acetic acid = 0.06N
Final strength = 0.042 N
Volume given = 50 mL
there Initial m moles of CH3COOH
= 0.06 x 50 = 3
Final m moles of CH3COOH
= 0.042 x 50 = 21
therefore, m moles of CH3COOH absorbed
= 3-2.1
= 0.9 m mol
Hence, mass of CH3COOH absorbed per gram of charcoal
= 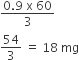
Consider separate solution of 0.500 M C2H5OH (aq), 0.100 M Mg3(PO4)2 (aq) 0.250 M KBr (aq) and 0.125 M Na3PO4 (aq) at 25oC. Which statement is true about these solutions, assuming all salts to be strong electrolytes?
-
They all have the same osmotic pressure
-
0.100 M Mg3(PO4)2 (aq) has the highest osmotic pressure
-
0.125 M Na3PO (aq) has the highest osmotic pressure
-
0.500 M C2H5OH (aq) has the higest osmotic pressure
A.
They all have the same osmotic pressure
effective molarity = Van't Hoff factor x molarity
0.5 M C2H5OH (aq) i =1
Effective molarity = 0.5
0.25 M KBr (aq) i = 2
Effective molarity = 0.5
0.1 M Mg3(PO4)2 (aq) i = 5
Effective molarity = 0.5 M
0.125 M Na3PO4 (aq)
Effective molarity = 0.5 M
Hence, all colligative properties are same
The molarity of a solution obtained by mixing 750 mL of 0.5 (M) HCl with 250 mL of 2(M) HCl will be
-
0.875 M
-
1.00 M
-
1.75 M
-
0.0975 M
A.
0.875 M
M1V1 + M2V2 = MV
M= 0.875
The density of a solution prepared by dissolving 120 g of urea (mol. Mass = 60 u ) in 1000g of water is 1.15 g/mL. The molarity of this solution is
-
0.50 M
-
1.78 M
-
1.02 M
-
2.05
D.
2.05
Total mass of solution
= 1000 g water +120 g urea
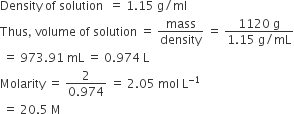
Kf for water is 1.86K kg mol–1.If your automobile radiator holds 1.0 kg of water, how many grams of ethylene glycol (C2H6O2) must you add to get the freezing point of the solution lowered to –2.8°C?
-
72 g
-
93 g
-
39 g
-
27 g
B.
93 g
Coolant is glycol (C2H6O2) and is non-electrolyte.
ΔTf =2.8°
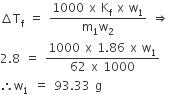
Ethylene glycol is used as an antifreeze in a cold climate. Mass of ethylene glycol which should be added to 4 kg of water to prevent it form freezing at - 6° C will be : (Kf for water = 1.86 K kg mol-1, and molar mass of ethylene glycol = 62g mol-1)
-
804.32 g
-
204.30 g
-
400.00 g
-
304.60 g
A.
804.32 g
ΔTf = iKfm
ΔTf = 6ºC
w1 = mass of ethylene glycol in grams
w2 = mass of solvent (H2O) in grams= 4000g
m1 = Molar mass of ethylene glycol = 62 g
i = 1
i is van't off factor
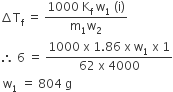
A vessel at 1000 K contains CO2 with a pressure of 0.5 atm. Some of the CO2 is converted into CO on the addition of graphite. If the total pressure at equilibrium is 0.8 atm, the value of K is
-
1.8 atm
-
3 atm
-
0.3 atm
-
0.3 atm
A.
1.8 atm
Kp depends upon the partial pressure of reactants and products so first calculate their partial pressure and then, calculate Kp,

In the context of the lanthanoids, which of the following statement is not correct?
-
There is a gradual decrease in the radii of the members with increasing atomic number in the series.
-
All the member exhibit +3 oxidation state.
-
Because of similar properties, the separation of lanthanoids is not easy.
-
Availability of 4f electrons results in the formation of compounds in +4 state for all the members of the series.
D.
Availability of 4f electrons results in the formation of compounds in +4 state for all the members of the series.
If sodium sulphate is considered to be completely dissociated into cations and anions in aqueous solution, the change in freezing point of water (ΔTf), when 0.01 mol of sodium sulphate is dissolved in 1 kg of water, is (Kf = 1.86 K kg mol–1).
-
0.0372 K
-
0.0558 K
-
0.0744 K
-
0.0186 K
B.
0.0558 K
Na2SO4 → 2Na+ + SO42-
Van't Hoff factor of dissociation for Na2SO3 = 3
Molality of the solution = 0.01 m
ΔTf = i x Kf x m
= 3 x 1.86 x 0.01
= 0.0558 K
On mixing, heptane and octane form an ideal solution. At 373 K, the vapour pressures of the two liquid components (heptane and octane) are 105 kPa and 45 kPa respectively.Vapour pressure of the solution obtained by mixing 25.0 g of heptane and 35 g of octane will be (molar mass of heptane = 100 g mol–1 and of octane =114 g mol–1)
-
144.5 kPa
-
72.0 kPa
-
36.1 kPa
-
96.2 kPa
B.
72.0 kPa
Vapour pressure of the solution can be calculated by the formula
pT = XHp°H + Xo.P°o.
Therefore calculate the mole fractions of heptane and octane
pT = XHp°H + Xo.P°o.
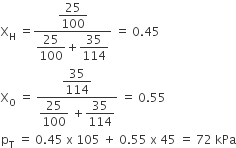
The freezing point of benzene decreases by 0.45°C when 0.2 g of acetic acid is added to 20 g of benzene. If acetic acid associates to form a dimer in benzene, percentage association of acetic acid in benzene will be
(Kf for benzene = 5.12 K kg mol–1)
-
64.6%
-
80.4%
-
74.6%
-
94.6%
D.
94.6%
In benzene
2CH3COOH ⇌ (CH3COOH)2
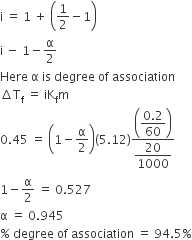
On treatment of 100 mL of 0.1 M solution of CoCl3 . 6H2O with excess AgNO3; 1.2 × 1022 ions are precipitated. The complex is
-
[Co(H2O)4 Cl2]Cl.2H2O
-
[Co(H2O)3Cl3].3H2O
-
[Co(H2O)6]Cl3
-
[Co(H2O)5Cl]Cl2.H2O
D.
[Co(H2O)5Cl]Cl2.H2O
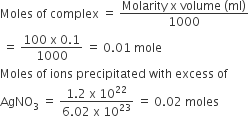
Number of Cl– present in ionization sphere =
It means 2Cl– ions present in ionization sphere
∴ complex is [Co(H2O)5Cl]Cl2.H2O
1 gram of a carbonate (M2CO3) on treatment with excess HCl produces 0.01186 mole of CO2. The molar mass of M2CO3 in g mol-1 is
-
1186
-
84.3
-
118.6
-
11.86
B.
84.3
Given chemical equation
M2CO3 +2HCl → 2MCl + H2O + CO2
1 gm 0.01186 mol
From the balanced chemical equation
1/M = 0.01186
M = 84.3 gm/mol
A binary liquid solution is prepared by mixing n-heptane and ethanol. Which one of the following statements is correct regarding the behaviour of the solution?
-
The solution formed is an ideal solution
-
The solution is non-ideal, showing +ve deviation from Raoult’s law.
-
The solution is non-ideal, showing –ve deviation from Raoult’s law.
-
n-heptane shows +ve deviation while ethanol shows –ve deviation from Raoult’s law.
B.
The solution is non-ideal, showing +ve deviation from Raoult’s law.
On mixing n-heptane and ethanol; strong interactions are replaced by weak interaction and hence it kes non-ideal solution with positive deviation.
At 80o C, the vapour pressure of pure liquid ‘A’ is 520 mm Hg and that of pure liquid ‘B’ is 1000 mm Hg. If a mixture solution of ‘A’ and ‘B’ boils at 80o C and 1 atm pressure, the amount of ‘A’ in the mixture is (1 atm = 760 mm Hg)
-
52 mol percent
-
34 mol percent
-
48 mol percent
-
50 mol percent
D.
50 mol percent
PT = PoXA + PoXB
760 = 520XA+ PoB(1-XA)
⇒ = 0.5
Thus, mole% of A = 50%
Equal masses of methane and oxygen are mixed in an empty container at 25ºC. The fraction of the total pressure exerted by oxygen is
-
2/3
-
(1/3) x (273 / 298)
-
1/3
-
1/2
C.
1/3
Let the mass of methane and oxygen is w
mole fraction of oxygen

Let the total pressure be P The pressure exerted by oxygen (partial pressure) = XO2 × Ptotal
P =1/3
A 5.25% solution of a substance is isotonic with a 1.5% solution of urea (molar mass = 60 g mol–1) in the same solvent. If the densities of both the solutions are assumed to be equal to 1.0 gcm–3, molar mass of the substance will be –
-
90.0g mol–1
-
115.0g mol–1
-
105.0g mol–1
-
210.0 g mol–1
D.
210.0 g mol–1
Solutions with the same osmotic pressure are isotonic
Let the molar mass of the substance be M
π1 =C1RT=C2RT =π2
So, C1 = C2
As density of the solutions are same
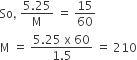
The density (in g mL–1) of a 3.60 M sulphuric acid solution that is 29% H2SO4 (Molar mass = 98 g mol-) by mass will be
-
1.64
-
1.88
-
1.22
-
1.45
C.
1.22
Let the density of solution be ‘d’
Molarity of solution given = 3.6
i.e. 1 litre of solution contains 3.6 moles of H2SO4
or 1 litre of solution contains 3.6 × 98 gms of H2SO4
Since, the solution is 29% by mass.
100 gm solution contains 29 gm H2SO4
100/d ml l solution contains 29 gm of H2SO4.
1000 ml solution contains 3.6 × 98 gm of H2SO4
![]()
d = 1.22
A mixture of ethyl alcohol and propyl alcohol has a vapour pressure of 290 mm at 300 K. The vapour pressure of propyl alcohol is 200 mm. If the mole fraction of ethyl alcohol is 0.6, its vapour pressure (in mm) at the same temperature will be
-
350
-
300
-
360
-
700
A.
350
Let the vapour pressure of pure ethyl alcohol be P,
According to Raoult’s law 290 = 200 × 0.4 + P × 0.6
P = 290-80/0.6 = 350 mm Hg
6.02×1020 molecules of urea are present in 100 ml of its solution. The concentration of urea solution is
-
0.001 M
-
0.1 M
-
0.02 M
-
0.01 M
D.
0.01 M
Avogadros number NA = 6.02 x 1023 = 1 mole
∴ 6.02 x 1020 molecules
= 0.001 mole in 100 mL (0.1 L solution)
∴ Molar concentration = mol/volume in L
=0.001/0.1
= 0.01 M
To neutralize completely 20 mL of 0.1 M aqueous solution of phosphorous acid (H3PO3), the volume of 0.1 M aqueous KOH solution required is
-
10 mL
-
60 mL
-
40 mL
-
20 mL
C.
40 mL
H3PO3 is a dibasic acid (containing two ionizable protons attached to O directly)
H3PO3 ⇌ 2H+ + HPO42-
0.1 M H3PO3 = 0.2 N H3PO3
0.1 M KOH = 0.1 N KOH
N1V1 = N2V2
(KOH) = (H3PO3)
0.1 V1 = 0.2 x 20
V1 = 40 mL
Which of the following liquid pairs shows a positive deviation from Raoult’s law?
-
Water – hydrochloric acid
-
Acetone – chloroform
-
Water – nitric acid
-
Benzene – methanol
D.
Benzene – methanol
Water and hydrochloric acid; and water and nitric acid form miscible solutions. They show no deviation.
Which one of the following statements is false?
-
Raoult’s law states that the vapour pressure of a components over a solution is proportional to its mole fraction
-
Two sucrose solutions of same molality prepared in different solvents will have the same freezing point depression
-
The correct order of osmotic pressure for 0.01 M aqueous solution of each compound is BaCl2 > KCl > CH3COOH > sucrose
-
The osmotic pressure (π) = MRT, where M is the molarity of the solution
B.
Two sucrose solutions of same molality prepared in different solvents will have the same freezing point depression
(a)pA = XA pAo : true
(b) ΔTf =Kfm
Kf is dependent on solvent
Thus is dependent on solvent
Thus freezing points [= t(solvent)- ΔTf) are different.
(c) i = [1 + (y-1) x]
y = number of ions
x = degree of ionisation
i = 3 for BaCl2 x = 1 (strong electrolyte)
i = 2 for KCl x = 1 (strong electrolyte)
i = (1+x) for CH3COOH x<i = (for BaCl2)>KCl>CH3COOH>Sucrose
(d) π = imRT = = MRT ; true (if van't Hoff factor i = 1
For 1 molal aqueous solution of the following compounds, which one will show the highest freezing point?
[Co(H2O)3 Cl3].3H2O
[Co(H2O)6]Cl3
[Co(H2O)5Cl] Cl2.H2O
[Co(H2O)4Cl2]Cl.2H2O
A.
[Co(H2O)3 Cl3].3H2O
The complex giving least number of ions will have lowest depression in freezing point and therefore highest freezing point.(Van’t Hoff factor = 1)
An aqueous solution contains an unknown concentration of Ba2+. When 50 mL of a 1 M solution of Na2SO4 is added, BaSO4 just begins to precipitate. The final volume is 500 mL. The solubility product of BaSO4 is 1 x 10–10. What is the original concentration of Ba2+?
1.0 x 10–10 M
5 x 10–9 M
2x10–9 M
1.1 x 10–9M
D.
1.1 x 10–9M
For the calculation of [Ba+2] in original solution (450 ml)
Which of the following statements about the composition of the vapour over an ideal 1:1 molar mixture of benzene and toluene is correct? Assume that the temperature is constant at 250C.
(Given, vapour pressure data at 250C benzene = 12.8 kPa, toluene = 3.85 kPa)
-
The vapour will contain a higher percentage of toluene
-
The vapour will contain equal amounts of benzene and toluene
-
Not enough information is given to make a prediction
-
The vapour will contain a higher percentage of benzene
D.
The vapour will contain a higher percentage of benzene
A component having vapour pressure will have a higher percentage in the vapour phase. Benzene has vapour pressure 12.8 kPa which is greater than toluene 3.85pKa. Hence, the vapour will contain a higher percentage of benzene.
which is one not equal to zero for an ideal solution?
- ΔHmix
- ΔSmix
- ΔVmix
- ΔP=Pobserved-PRaoult
B.
ΔSmixFor an ideal solution
i) There will no change in volume on mixing the two components i.e. ΔVmixing =0
ii) There will no change in volume of ΔHmixing =0 so, ΔSmix not equal to for an ideal solution.
A mixture of gases contains H2 and O2 gases in the ratio of 1:4 (w/w).what is the molar ratio of the two gases in the mixture?
-
1:4
-
4:1
-
16:1
-
2:1
B.
4:1
Let the mass of H2 gas be x g and mass of O2 gas 4x g
Molar H2 : O2
mass 2 : 32
therefore, Molar ratio =
The boiling point of 0.2 mol kg-1 solution of X in water is greater than the equimolal solution of Y in water. Which one of the following statements is true is this case?
-
X is undergoing dissociation in water
-
The molecular mass of X is greater than the molecular mass of Y.
-
Molecular mass of X is less than the molecular mass of Y,
-
Y is undergoing dissociation in water while X undergoes no change.
A.
X is undergoing dissociation in water
Molality of solution X = molality of solution Y = 0.2
we know that elevation in the boiling point( ΔTb ) of a solution is proportional to the molal concentration of the solution i.e.
ΔTb = Kbm
where, m is the molality of the solution and Kb is molal boiling point constant or ebullioscopic constant.
therefore,
By elevation in boiling point relation
ΔTb = iKbm or ΔTb directly proportional to i
where i is van't Hoff is a factor
Since ΔTb of solution X is greater than ΔTb of solution Y.
(observed colligative property is greater than normal colligative property).
therefore, i of solution > i of solution Y
therefore solution X undergoing dissociation.
Of the following 0.10 m aqueous solutions, which one will exhibit the largest freezing point depression?
-
KCl
-
C6H12O6
-
Al2(SO4)3
-
K2SO4
C.
Al2(SO4)3
ΔTf (freezing point depression) is a colligative property and depends upon the van't Hoff factor (i) i,e., number of ions given by the electrolyte in aqueous solution.ΔTf =i x Kf xm
where Kf = molal freezing point depression constant
m =mnolality of the solution
therefore,
Kf and m are constant ΔTf
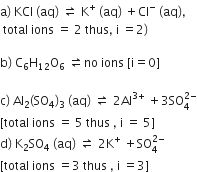
Hence, Al2(SO4)3 will exhibit largest freezing point depression due to the highest value of i.
The weight of silver (at. wt. = 108) displaced by a quantity of electricity which displaces 5600 mL of O2 at STP will be
-
5.4 g
-
10.8 g
-
54.0 g
-
108 g
D.
108 g
Since, 22400 mL volume is occupied by 1 mole of O2 STP.
Thus, 5600 mL of O2 means =

Vapour pressure of chloroform (CHCl3) and dichloromethane (CH2Cl2) at 25oC are 200 mmHg and 41.5 mmHg respectively, Vapour pressure of the solution obtained by mixing 25.5 g of CHCl3 and 40 g of CH2Cl2 at the same temperature will be
(molecular mass of CHCl3= 119.5 u and molecular mass of CH2Cl2 = 85 u)
-
173.9 mmHg
-
615.0 mmHg
-
347.9 mmHg
-
28.5 mmHg
A.
173.9 mmHg
Number of moles of CHCl3
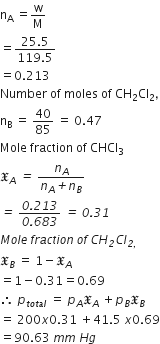
The van't Hoff factor, i for a compound which undergoes dissociation in one solvent and association in other solvent is respectively.
-
Less than one and less than one
-
Greater than one and less than one
-
Greater than one and greater than one
-
less than one and greater than one
B.
Greater than one and less than one
For dissociation, i > 1.
For association, i <1.
An aqueous solution is 1.00 molal in KI. Which change will cause the vapour pressure of the solution to increase?
-
Addition of NaCl
-
Addition of Na2SO4
-
Addition of 1.00 molal KI
-
addition of water
D.
addition of water
Vapour pressure depends upon the surface area of the solution. Larger the surface area, higher is the vapour pressure.
The addition of solute decreases the vapour pressure as some sites of the surface are occupied by solute particles, resulting in decreased surface area. However, the addition of solvent, ie, dilution increases the surface area of the liquid surface, thus results in increased vapour pressure.
Hence, the addition of water to the aqueous solution of (1 molal) KI, result in increased vapour pressure.
What is the [OH-] in the final solution prepared by mixing 20.0 mL of 0.50 M HCl with 30.0mL of 0.10 Ba(OH)2?
-
0.10 M
-
0.40 M
-
0.0050 M
-
0.12 M
A.
0.10 M
Number of milliequivalents of HCl = 2 x 0.050 x 1 = 1
Number of milliequivalents of Ba(OH)2 = 2 x 30 x 0.10 = 6
[OH]- of final soluton
milliequivalent of Ba(OH)2
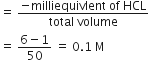
A 0.0020 m aqueous solution of an ionic compound Co(NH3)5(NO2)Cl freezes at -0.00732o C . Number of moles of ions which 1 mol of ionic compound produces on being dissolved in water will be (kf = - 1.86o C/m)
-
2
-
3
-
4
-
1
A.
2
Given,
molality = 0.0020 m
Δ Tf = 0o C -0.007320 C
kf = 1.86 oC/m
ΔTf = i.kf x m
i = ΔTf/ kf x m
= 0.00732/1.82 x 0.0020
= 1.92 = 2
A solution containing 10 g per dm3 is urea (molecular mass = 60 g mol-1) is isotonic with a molecular mass of this non-volatile solute. The molecular mass of this of this non-volatile solute is:
-
250 g mol-1
-
300 g mol-1
-
350 g mol-1
-
200 g mol-1
B.
300 g mol-1
10 g per dm3 of urea is isotonic with 5% solution of a non-volatile solute. Hence, between this solution osmosis is not possible so, their molar concentrations are equal to each other,
Thus, molar concentration of urea solution

1.00 g of a non- electrolyte solute (molar mass 250 g mol-1) was dissolved in 51.2 g of benzene. If the freezing point depression constant, Kf of benzene is 5.12 K Kg mol-1, the freezing point of benzene will be lowered by:
-
0.4 K
-
0.3 K
-
0.5 K
-
0.2 K
A.
0.4 K
Molality of non- electrolyte solute
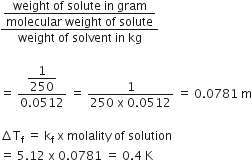
A solution of acetone in ethanol:
-
shows a negative deviation from Raoult's law
-
shows a positive deviation from Raoult's law
-
behave likea near ideal solution
-
obeys Raoult's law
B.
shows a positive deviation from Raoult's law
A solution ofacetone in ethanol shows a positive deviation from Raoult's law due to miscibility of these two liquids with a difference of polarity and length of the hydrocarbon chain.
During osmosis, flow of water through a semi-permeable membrane is:
-
from a solution having higher concentration only
-
from both sides of a semi-permeable membrane with equal flow rates
-
from both sides of a semi-permeable membrane with unequal flow rates
-
from a solution having lower concentration only
D.
from a solution having lower concentration only
During osmosis, the flow of water through a semi-permeable membrane is from a solution having lower concentration only.
If molality of the dilute solution is doubled, the value of molal depression constant (Kf) will be
-
Doubled
-
Halved
-
Tripled
-
Unchanged
D.
Unchanged
Kf (molal depression constant) is a characteristic of solvent and is independent of molality.
Which of the following is dependent on temperature?
-
Molality
-
Molarity
-
Mole fraction
-
Weight percentage
B.
Molarity
Molarity includes volume of solution which can change with change in temperature.
The normality of 10% (w/v) of acetic acid is
1 N
1.3 N
1.7 N
1.9 N
C.
1.7 N
Normality is given as,
Consider the following solutions,
A = 0.1 M glucose,
B = 0.05 M NaCl,
C = 0.05 M BaCl2
D = 0.1 M AlCl3
Which of the following pairs is isotonic?
A and B
A and D
A and C
B and C
A.
A and B
Isotonic solutions have a same molar concentration of solute particles in solution. Molar concentration of particles in solution are,
(a) = 0.1 M in glucose
(b) = 2 x 0.05 M in NaCl2
(c) = 3 x 0.05 M in BaCl2
(d) = 4 x 0.1 M in AlCl3
Hence, 0.1 M glucose and 0.05 and
Which of the following aqueous solution should have a highest boiling point?
1.0 M NaOH
1.0 M Na2SO4
1.0 M NH4NO3
10 MKNO3
B.
1.0 M Na2SO4
It depends on the Van't Hoff factor.
Van't Hoff factor is directly proportional to the boiling point.
In the case of Na2SO3, i is maximum = 3
Hence it has maximum boiling points.
Combustion of glucose takes place according to the equation.
C6H12O6 + 6O2 → 6CO2 + 6H2O
Δ = - 72 k-cal
The energy required for combustion of 1.6 g of glucose is
0.064 kcal
0.64 kCal
6.4 kcal
64 kcal
B.
0.64 kCal
Molar mass of C6H12O6 = 180 g mol-1
∵ 180 g of glucose require energy = 72 kcal
∴ 1.6 g of glucose require energy = 72 x 1.6/180
= 0.64 k cal
when the heat of reaction at constant pressure is -2.5 x 103 cal can entropy change is 7.4 cal deg-1 at 25oC, the reaction is predicted as
reversible
Spontaneous
non -spontaneous
Irreversible
B.
Spontaneous
For the reaction at constant pressure,
ΔH = - 2.5 x 103 cal
ΔS = 7.4 cal deg-1
∴ ΔG = ΔH -TΔS
= (-)2.5 x 103 - 298 x 7.4
= - 2.5 x 103 - 2205.2
ΔG = - 4705 cal
Hence, reaction is spontaneous.
The volume of water to be added to 100 cm3 of 0.5 NH2SO4 to get decinormal concentration is
100 cm3
450 cm3
500 cm3
400 cm3
D.
400 cm3
N1V1 = N2V2
Given, N1 = 0.5 N, N2 = 0.1 N
V1 = 100 cm3 (Total final volume)
Therefore, Volume to be added
= 500- 100 = 400 cm3
Mock Test Series
Sponsor Area
Sponsor Area