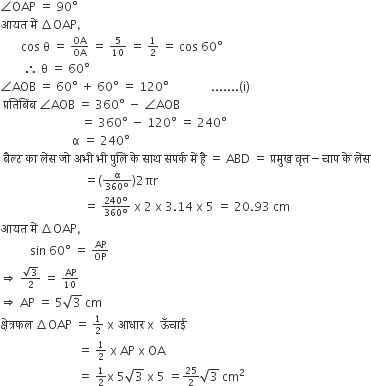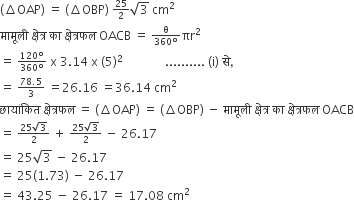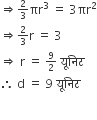गणित Chapter 13 पृष्ठीय क्षेत्रफल और आयतन
Sponsor Area
NCERT Solution For Class 10 गणित गणित
दो घनों, जिनमें से प्रत्येक का आयतन 64 cm3 है, के सलंग्न फलकों को मिलाकर एक ठोस बनाया जाता है। इससे प्राप्त घनाभ का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
माना दिए गए प्रत्येक घन की भुजा = a cm
प्रश्नानुसार,
दिए गए प्रत्येक घन का आयतन = 64 cm3



 a = 4
a = 4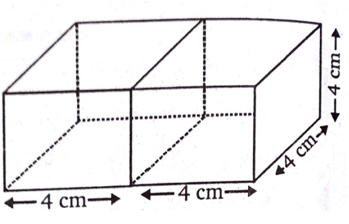
अब दो घनों को मिलाकर रखने से बने घनाभ के लिए
लंबाई(l) = (4+4)cm = 8 cm
चौड़ाई (b) = 4 cm
ऊँचाई (h) = 4 cm
∴ घनाभ का पृष्ठीय क्षेत्रफल = 2 (lb + bh + hl)
= 2(8 x 4 + 4 x 4 + 4 x 8)cm2
= 2(32+16+32)cm2
= 2 x 80 cm2 = 160 cm2
कोई बर्तन एक खोखले अर्धगोले के आकर का है जिसके ऊपर एक खोखला बेलन अध्यारोपित है। अर्धगोले का व्यास 14cm है और इस बर्तन (पात्र) की कुल ऊँचाई 13cm है। इस बर्तन का आंतरिक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, बर्तन के अर्धगोले का व्यास = 14 cm
बर्तन के अर्धगोले की त्रिज्या (r) = 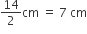
बर्तन के अर्धगोले का पृष्ठीय क्षेत्रफल = 
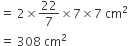

बर्तन के बेलनाकार भाग की त्रिज्या (r) = 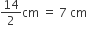
बर्तन के बेलनाकार भाग की ऊँचाई (h) = (13 - 7)cm = 6 cm
बर्तन के बेलनाकार भाग का वक्र पृष्ठीय क्षेत्रफल = 
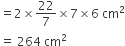
अत: बर्तन का आंतरिक पृष्ठीय क्षेत्रफल = (308 + 264) cm2
= 572 cm2
एक खिलौना त्रिज्या 3.5 cm वाले एक शंकु के आकर का हो, जो उसी त्रिज्या वाले एक अर्धगोले पर अध्यारोपित है। इस खिलौने की सम्पूर्ण ऊँचाई 15.5 cm है। इस खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
खिलौने के अर्धगोलाकार भाग की त्रिज्या (r) = 3.5 cm
खिलौने के अर्धगोलाकार भाग का पृष्ठीय क्षेत्रफल = 
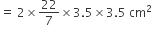
= 77 cm2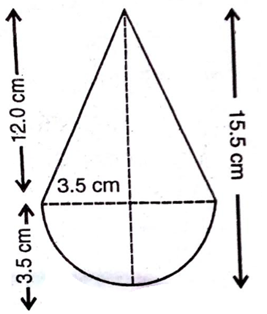
खिलौने के शंकु वाले भाग की त्रिज्या (r) = 3.5 cm
खिलौने के शंकु वाले भाग की ऊँचाई (h) = (15.5 - 3.5)cm = 12 cm
खिलौने के शंकु वाले भाग की तिर्यक ऊँचाई (l) = 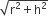
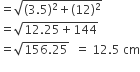
खिलौने के शंकु वाले भाग का पृष्ठीय क्षेत्रफल = 
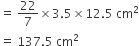
अत: खिलौने का संपूर्ण पृष्ठीय क्षेत्रफल = (अर्धगोलाकार + शंकु वाले भाग का पृष्ठीय क्षेत्रफल)
= (77+137.5)cm2 = 214.5 cm2
भुजा 7cm वाले एक घनाकार ब्लॉक के ऊपर एक अर्धगोला रखा हुआ है। अर्धगोले का अधिकतम व्यास क्या हो सकता है? इस प्रकार बने ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, घनाकार ब्लॉक की भुजा = 7 cm
प्रश्नानुसार अर्धगोले का अधिकतम व्यास = घनाकार ब्लॉक की भुजा  अर्धगोले का अधिकतम व्यास = 7 cm
अर्धगोले का अधिकतम व्यास = 7 cm अर्धगोले की त्रिज्या (r) =
अर्धगोले की त्रिज्या (r) = 

घनाकार ब्लॉक का पृष्ठीय क्षेत्रफल = 6(भुजा)2
= 6 x 7 x 7 cm2
= 294 cm2
अर्धगोले का पृष्ठीय क्षेत्रफल =
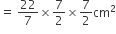
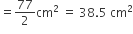
अत: पूर्ण ठोस का पृष्ठीय क्षेत्रफल = (294 + 38.5) cm2
= 332.5 cm2
एक घनाकार ब्लॉक के एक फलक को अंदर की ओर से काटकर एक अर्धगोलाकार गड्डा इस प्रकार बनाया गया है कि अर्धगोले का व्यास l घन के एक किनारे के बराबर है। शेष बचे ठोस का पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, घनाकार ब्लॉक की भुजा = l मात्रक
∴ घनाकार ब्लॉक का पृष्ठीय क्षेत्रफल = 6(भुजा)2
= 6l2 वर्ग मात्रक
अर्धगोले का व्यास = l मात्रक
अर्धगोले की त्रिज्या (r) = 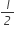 मात्रक
मात्रक
∴ अर्धगोले का पृष्ठीय क्षेत्रफल = 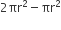

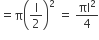 वर्ग मात्रक
वर्ग मात्रक
अत: शेष बचे ठोस का पृष्ठीय क्षेत्रफल 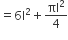
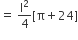 वर्ग मात्रक
वर्ग मात्रक
दवा का एक कैप्सूल (capsule) एक बेलन के आकर का है जिसके दोनों सिरों पर एक-एक अर्धगोला लगा हुआ है (देखिए आकृति)। पूरे कैप्सूल की लंबाई 14 mm है और उसका व्यास 5 mm है। इसका पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, कैप्सूल के बेलनाकार भाग का व्यास = 5 mm
कैप्सूल के बेलनाकार भाग की त्रिज्या (r) = 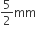
कैप्सूल के बेलनाकार भाग की ऊँचाई (h) = 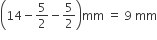
 कैप्सूल के बेलनाकार भाग का पृष्ठीय क्षेत्रफल =
कैप्सूल के बेलनाकार भाग का पृष्ठीय क्षेत्रफल = 
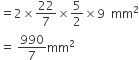
कैप्सूल के दोनों अर्धवृत्ताकार सिरों की त्रिज्या (r) = 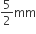
 कैप्सूल के दोनों अर्धवृत्ताकार सिरों का पृष्ठीय क्षेत्रफल =
कैप्सूल के दोनों अर्धवृत्ताकार सिरों का पृष्ठीय क्षेत्रफल = 
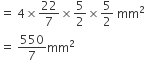
अत: कैप्सूल का कुल पृष्ठीय क्षेत्रफल = 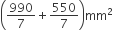
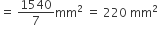
कोई तम्बू एक बेलन के आकर का है जिस पर एक शंकु अध्यारोपित है। यदि बेलनाकार भाग की ऊँचाई और व्यास क्रमश: 2.1 m और 4 m है तथा शंकु की तिर्यक ऊँचाई 2.8 m है तो इस तंबू को बनाने में प्रयुक्त कैनवस (canvas) का क्षेत्रफल ज्ञात कीजिए। साथ ही, 500रु प्रति m2 की दर से इसमें प्रयुक्त कैनवस की लागत ज्ञात कीजिए।(ध्यान दीजिए की तंबू के आधार को कैनवस से नहीं ढका जाता है।)
यहाँ पर, तंबू के बेलनाकार भाग का व्यास = 4 m
तंबू के बेलनाकार भाग की त्रिज्या (r) = 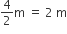
तंबू के बेलनाकार भाग की ऊँचाई (h) = 2.1 m तंबू के बेलनाकार भाग का एक पृष्ठीय क्षेत्रफल =
तंबू के बेलनाकार भाग का एक पृष्ठीय क्षेत्रफल = 
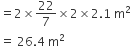
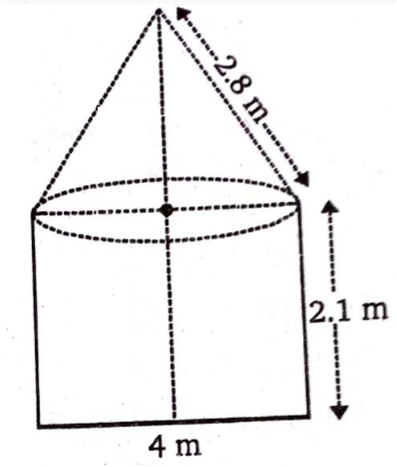
तंबू के शंकु वाले भाग की त्रिज्या (r) = 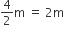
तंबू के शंकु वाले भाग की तिर्यक ऊँचाई (l) = 2.8 m तंबू के शंकु वाले भाग का वक्र पृष्ठीय क्षेत्रफल =
तंबू के शंकु वाले भाग का वक्र पृष्ठीय क्षेत्रफल = 
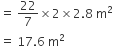
अत: तंबू बनाने के लिए आवश्यक कैनवस का क्षेत्रफल = (26.4 + 17.6)m2 = 44 m2
1m2 कैनवस की लागत = 500 रु
44m2 कैनवस की लागत = 44 x 500 रु = ₹22000
ऊँचाई 2.4cm और व्यास 1.4 cm वाले एक ठोस बेलन में से इसी ऊँचाई और इसी व्यास वाला एक शंक्वाकार खोल (cavity) काट लिया जाता है। शेष बचे ठोस का निकटतम वर्ग सेंटीमीटर तक पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
बेलनाकार ठोस का व्यास = 1.4 cm
बेलनाकार ठोस की त्रिज्या (r1) = 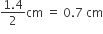
बेलनाकार ठोस की ऊँचाई (h1) = 2.4 cm
 बेलनाकार ठोस का वक्र पृष्ठीय क्षेत्रफल (A1) =
बेलनाकार ठोस का वक्र पृष्ठीय क्षेत्रफल (A1) = 
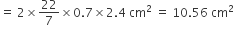
तथा बेलनाकार ठोस के आधार का क्षेत्रफल (A2) = 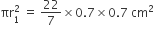
= 1.54 cm2
काटे गए शंक्वाकार खोल की तिर्यक ऊँचाई (l1) = 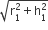
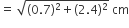
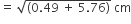

 काटे गए शंक्वाकार खोल का वक्र पृष्ठीय क्षेत्रफल (A3) =
काटे गए शंक्वाकार खोल का वक्र पृष्ठीय क्षेत्रफल (A3) = 
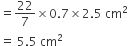
अत: शेष बचे ठोस का पृष्ठीय क्षेत्रफल = A1 + A2 + A3
= (10.56 + 1.54 + 5.5)cm2
= 17.6 cm2
लकड़ी के एक ठोस बेलन के प्रत्येक सिरे पर एक अर्धगोला खोदकर निकलते हुए, एक वस्तु बनाई गई हैं, जैसा कि आकृति में दर्शाया गया है। यदि बेलन की ऊँचाई 10 cm है और आधार की त्रिज्या 3.5 cm है तो इस वस्तु का सम्पूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, दिए गए ठोस बेलन के
आधार की त्रिज्या (r) = 3.5 cm
दिए गए ठोस बेलन की ऊँचाई (h) = 10 cm दिए गए ठोस बेलन का वक्र पृष्ठीय क्षेत्रफल (A1) =
दिए गए ठोस बेलन का वक्र पृष्ठीय क्षेत्रफल (A1) = 
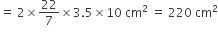

निकाले गए प्रत्येक अर्धगोले की त्रिज्या (r) = 3.5 cm निकाले गए दोनों अर्धगोलों का पृष्ठीय क्षेत्रफल (A2) =
निकाले गए दोनों अर्धगोलों का पृष्ठीय क्षेत्रफल (A2) = 
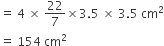
अत: दी गई वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल = A1 + A2
= (220 + 154)cm2
= 374 cm2
एक ठोस एक अर्धगोले पर खड़े एक शंकु के आकर का है जिनकी त्रिज्याएँ 1 cm हैं तथा शंकु की ऊँचाई उसकी त्रिज्या के बराबर है। इस ठोस का आयतन  के पदों में ज्ञात कीजिए।
के पदों में ज्ञात कीजिए।
यहाँ पर,
दिए गए ठोस के अर्धगोलाकार भाग की त्रिज्या (r) = 1 cm
दिए गए ठोस के शंक्वाकार भाग की त्रिज्या (r) = 1 cm
दिए गए ठोस के शंक्वाकार भाग की ऊँचाई (h) = 1 cm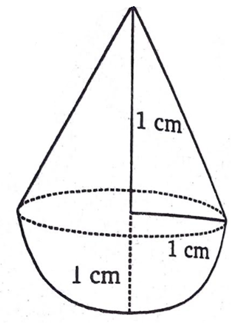
अत: दिए गए ठोस का आयतन = (अर्धगोलाकार भाग + शंक्वाकार भाग) का आयतन
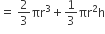
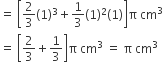
एक इंजीनियरिंग के विद्यार्थी रचेल से एक पतली एल्युमीनियम की शीट का प्रयोग करते हुए एक मॉडल बनाने को कहा गया जो एक ऐसे बेलन के आकर का हो जिसके दोनों सिरों पर दो शंकु जुड़े हुए हों। इस मॉडल का व्यास 3 cm है और इसकी लंबाई 12cm है। यदि प्रत्येक शंकु की ऊँचाई 2cm हो तो रचेल द्वारा बनाए मॉडल में अन्तर्विष्ट हवा का आयतन ज्ञात कीजिए। (यह मान लीजिए की मॉडल की आंतरिक और बाहरी विमाएँ लगभग बराबर हैं।)
मॉडल के बेलनाकार भाग की त्रिज्या (r1) = 
मॉडल के बेलनाकार भाग की ऊँचाई (h1) = (12 - 2 x 2)cm
= 8 cm
मॉडल के प्रत्येक शंक्वाकार भाग की त्रिज्या (r2) = 
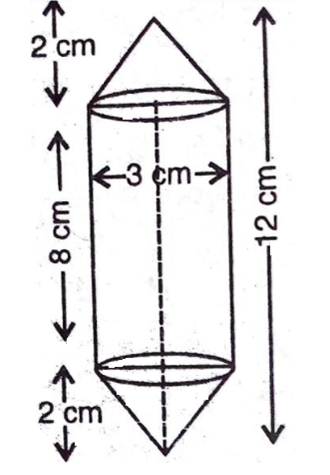
मॉडल के प्रत्येक शंक्वाकार भाग की ऊँचाई (h2) = 2 cm
मॉडल में अन्तर्विष्ट हवा का आयतन = (बेलनाकार भाग + दोनों शंक्वाकार भागों) का आयतन
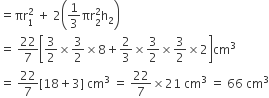
एक गुलाबजामुन में उसके आयतन की लगभग 30% चीनी की चाशनी होती है। 45 गुलाबजामुनों में लगभग कितनी चाशनी होगी, यदि प्रत्येक गुलाबजामुन एक बेलन के आकर का है, जिसके दोनों सिरे अर्धगोलाकार हैं तथा इसकी लम्बाई 5cm और व्यास 2.8 cm है।
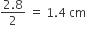
गुलाबजामुन के बेलनाकार भाग की ऊँचाई (h1) = (5 - 1.4 x 2)cm
= 2.2 cm
गुलाबजामुन के प्रत्येक अर्धगोलाकार भाग की त्रिज्या (r2) =
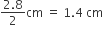

अत: 1 गुलाबजामुन का आयतन = (बेलनाकार भाग + दोनों शंक्वाकार भागों) का आयतन
=
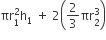
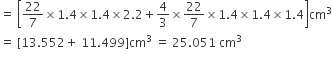
 45 गुलाबजामुनों का आयतन
45 गुलाबजामुनों का आयतन 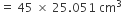

अत: 45 गुलाबजामुनों में चीनी की चाशनी की मात्रा =
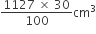
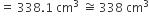
एक बर्तन एक उल्टे शंकु के आकर का है। इसकी ऊँचाई 8cm है और इसके ऊपरी सिरे (जो खुला हुआ है) की त्रिज्या 5 cm है। यह ऊपर तक पानी से भरा हुआ है। जब इस बर्तन में सीसे की कुछ गोलियॉं जिनमें प्रत्येक 0.5 cm त्रिज्या वाला एक गोला है, डाली जाती हैं, तो इसमें से भरे हुए पानी का एक चौथाई भाग बाहर निकल जाता है। बर्तन में डाली गई सीसे की गोलीयों की संख्या ज्ञात कीजिए।
यहाँ पर,
शंकु के आकार के बर्तन की त्रिज्या (r1) = 5 cm
शंकु के आकार के बर्तन की ऊँचाई (h) = 8 cm
शंकु के आकार के बर्तन में पानी का आयतन 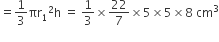
शंकु के आकार के बर्तन से बाहर निकल पानी का आयतन = 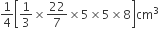
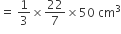
बर्तन में डाली गई प्रत्येक सीसे की गोली की त्रिज्या (r2) = 0.5 cm
बर्तन में डाली गई प्रत्येक सीसे की गोली का आयतन = 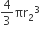
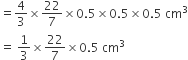
अत: बर्तन में डाली गई सीसे की गोलीयों की संख्या = 
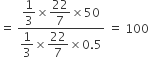
ऊँचाई 220 cm और आधार व्यास 24cm वाले एक बेलन, जिस पर ऊँचाई और त्रिज्या वाला एक बेलन आरोपित है, से लोहे का एक स्तंभ बना है। इस स्तंभ का द्रव्यमान ज्ञात कीजिए, जबकि दिया है लोहे का द्रव्यमान लगभग होता है। ( लीजिए।)
लीजिए।)
यहाँ पर, बड़े बेलन का व्यास = 24 cm
बड़े बेलन की त्रिज्या (R) = 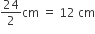
बड़े बेलन की त्रिज्या (H) = 220 cm
बड़े बेलन का आयतन (V1) = 
= 3.14 x 12 x 12 x 220 cm3
= 99475.2 cm3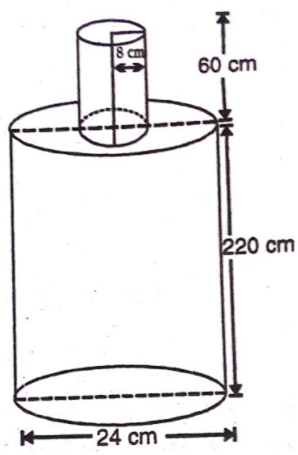
छोटे बेलन की त्रिज्या (r) = 8 cm
छोटे बेलन की ऊँचाई (h) = 60 cm
छोटे बेलन का आयतन (V2) = 
= 3.14 x 8 x 8 x 60 cm3
= 12057.6 cm3
स्तंभ में लगे कुल लोहे का आयतन = 
= (99475.2+12057.6)cm3
=111532.8 cm3
1 cm3 लोहे का द्रव्यमान = 8 g
111532.8 cm3 लोहे का द्रव्यमान = 111532.8 x 8 g

एक ठोस में, ऊँचाई 120cm और त्रिज्या 60cm वाला एक शंकु सम्मलित है, जो 60cm त्रिज्या वाले एक अर्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लम्ब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए।
यहाँ पर,
लंब वृत्तीय बेलनाकार बर्तन की त्रिज्या (R) = 60 cm
लंब वृत्तीय बेलनाकार बर्तन की ऊँचाई (H) = 180 cm
लंब वृत्तीय बेलनाकार बर्तन की आयतन (V1) = 
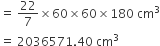
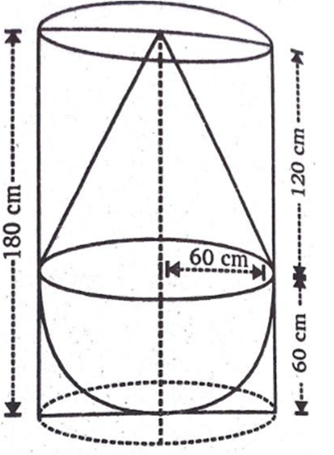
ठोस के शंक्वाकार भाग की त्रिज्या (r) = अर्धगोलाकार भाग की त्रिज्या
(r) = 60 cm
ठोस के शंक्वाकार भाग की ऊँचाई (h) = 120 cm
ठोस का आयतन (V2) = (शंक्वाकार भाग + अर्धगोलाकार भाग) का आयतन
= 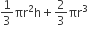
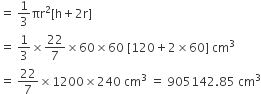
अत: बेलनाकार बर्तन में शेष बचे पानी की आयतन = V1 - V2
= (2036571.40 - 905142.85)cm3
= 1131428.55 cm3
= 1.131 m3 (लगभग)
एक गोलाकार काँच के बर्तन की एक बेलन के आकार की गर्दन है जिसकी लंबाई 8cm है और व्यास 2cm है जबकि गोलाकार भाग का व्यास 8.5 cm है। इसमें भरे जा सकने वाली पानी की मात्रा माप कर, एक बच्चे ने यह ज्ञात किया की इस बर्तन का आयतन 345 cm3 है। जाँच कीजिए कि उस बच्चे का उत्तर सही है या नहीं, यह मानते हुए कि उपरोक्त मापन आंतरिक मापन है और 
यहाँ पर,
बर्तन के बेलनाकार भाग का व्यास (d1) = 2 cm
बर्तन के बेलनाकार भाग की त्रिज्या (r1) = 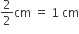
बर्तन के बेलनाकार भाग की ऊँचाई (h) = 8 cm
बर्तन के बेलनाकार भाग का आयतन (V1) = 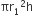
= 3.14 x 1 x 1 x 8 cm3
= 25.12 cm3
बर्तन के गोलाकार भाग का व्यास (d2) = 8.5 cm
बर्तन के गोलाकार भाग की त्रिज्या (r2) = 
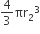
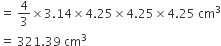
 बर्तन में भरे जा सकने वाले पानी का कुल आयतन = V1 + V2
बर्तन में भरे जा सकने वाले पानी का कुल आयतन = V1 + V2=[25.12 + 321.39] cm3
= 346.51 cm3
अत: बच्चे का उत्तर 345 cm3 सही नहीं है।
त्रिज्या 4.2 cm वाले धातु के एक गोले को पिघलाकर त्रिज्या 6cm वाले एक बेलन के रूप में ढाला जाता है। बेलन की ऊँचाई ज्ञात कीजिए।
यहाँ पर,
धातु के गोले की त्रिज्या (r) = 4.2 cm धातु के गोले का आयतन =
धातु के गोले का आयतन = 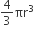
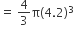 cm3
cm3
धातु के गोले को पिघलाकर बने बेलन की त्रिज्या (R) = 6 cm
माना
धातु के गोले को पिघलाकर बने बेलन की ऊँचाई = H cm
धातु के गोले को पिघलाकर बने बेलन का आयतन = 
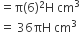
प्रश्नानुसार,
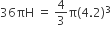

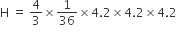

अत: धातु के गोले को पिघलाकर बने बेलन की ऊँचाई = 2.74 cm
Sponsor Area
क्रमश: 6cm, 8cm और 10 cm त्रिज्याओं वाले धातु के तीन ठोस गोलों को पिघलाकर एक बड़ा ठोस गोला बनाया जाता है। इस गोले की त्रिज्या ज्ञात कीजिए।
यहाँ पर,
पहले ठोस गोले की त्रिज्या (r1) = 6 cm
दूसरे ठोस गोले की त्रिज्या (r2) = 8 cm
तीसरे ठोस वाले गोले की त्रिज्या (r3) = 10 cm
माना तीनों ठोस गोलों को पिघलाकर
बने बड़े ठोस गोले की त्रिज्या = R cm
प्रश्नानुसार, बड़े ठोस गोले का आयतन = (पहले + दूसरे + तीसरे) ठोस गोलों का आयतन
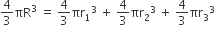
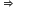
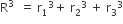 [दोनों ओर
[दोनों ओर  से भाग करने पर]
से भाग करने पर] 
= 216 + 512 + 1000 = 1728 = (12)3 R3 = 12
R3 = 12
अत: तीनों ठोस गोलों को पिघलाकर बने बड़े ठोस क्षेत्र गोले की त्रिज्या = 12 cm
व्यास 7 m वाला 20 m गहरा एक कुआँ खोदा जाता है और खोदने से निकली हुई मिट्टी को समान रूप से फैलाकर 22 m x 14 m वाला एक चबूतरा बनाया गया है। इस चबूतरे की ऊँचाई ज्ञात कीजिए।
यहाँ पर,
बेलनाकार कुएँ का व्यास = 7m
बेलनाकार कुएँ की त्रिज्या (r) = 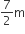
बेलनाकार कुएँ की गहराई (h) = 20 m बेलनाकार कुएँ को खोदकर निकली गई मिट्टी का आयतन
बेलनाकार कुएँ को खोदकर निकली गई मिट्टी का आयतन 
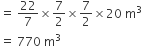
मिट्टी से बनने वाले चबूतरे का क्षेत्रफल = 22 x 14 m2
= 308 m2
अत: मिट्टी से बनने वाले चबूतरे की ऊँचाई = 
= 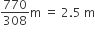
व्यास 3 m का एक कुआँ 14 m की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 4 m चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए, समान रूप से फैलाकर एक प्रकार का बाँध बनाया जाता है। इस बाँध की ऊँचाई ज्ञात कीजिए।
यहाँ पर, बेलनाकार कुएँ का व्यास = 3 m
बेलनाकार कुएँ की त्रिज्या (r) = 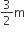
बेलनाकार कुएँ की गहराई (h) = 14 m बेलनाकार कुएँ को खोदकर निकाली गई मिट्टी का आयतन =
बेलनाकार कुएँ को खोदकर निकाली गई मिट्टी का आयतन = 
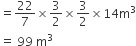
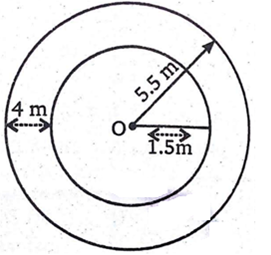
कुएँ की त्रिज्या (r) = 1.5 m
वृत्ताकार वलय (बांध) की चौड़ाई = 4.0 m
वृत्ताकार वलय की बाहरी त्रिज्या (R) = (1.5 + 4)m = 5.5 m
अब वृत्ताकार वलय (बाँध) का क्षेत्रफल = बाहरी क्षेत्रफल - आंतरिक क्षेत्रफल
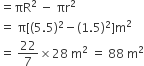
अत: बाँध की ऊँचाई = 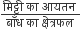

व्यास 12cm और ऊँचाई 15cm वाले एक लम्ब वृत्तीय बेलन के आकार का बर्तन आइसक्रीम से पूरा भरा हुआ है। इस आइसक्रीम को ऊँचाई 12cm और व्यास 6cm वाले शंकुओं में भरा जाना है, जिनका ऊपरी सिरा अर्धगोलाकार होगा। उन शंकुओं की संख्या ज्ञात कीजिए जो इस आइसक्रीम से भरे जा सकते हैं।
यहाँ पर,
आइसक्रीम के लिए बेलनाकार बर्तन का व्यास = 12 cm
आइसक्रीम के लिए बेलनाकार बर्तन की त्रिज्या (R) = 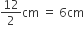
आइसक्रीम के लिए बेलनाकार बर्तन की ऊँचाई (H) = 15 cm आइसक्रीम के लिए बेलनाकार बर्तन का आयतन =
आइसक्रीम के लिए बेलनाकार बर्तन का आयतन = 
= 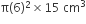

शंक्वाकार बर्तन का व्यास = 6 cm
शंक्वाकार बर्तन की त्रिज्या (r) = 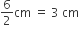
शंक्वाकार बर्तन की ऊँचाई (h) = 12 cm
शंक्वाकार बर्तन का आयतन 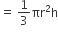
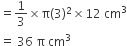
शंकु के ऊपर अर्धगोलाकार आइसक्रीम का आयतन = 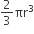
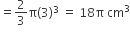
 प्रत्येक शंकु में आइसक्रीम का आयतन =
प्रत्येक शंकु में आइसक्रीम का आयतन = 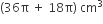
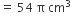
अत: आवश्यक शंकुओं की संख्या 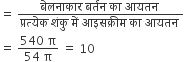
विमाओं 5.5 cm x 10 cm x 3.5 cm वाला एक घनाभ बनाने के लिए 1.75cm व्यास और 2 mm मोटाई वाले कितने चाँदी के सिक्कों को पिघलाना पड़ेगा?
यहाँ पर,
वांछित घनाभ का आयतन = 5.5 x 10 x 3.5 cm3
= 192.5 cm3
चाँदी के प्रत्येक सिक्के का व्यास = 1.75 cm
चाँदी के प्रत्येक सिक्के की त्रिज्या (r) = 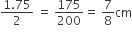
चाँदी के प्रत्येक सिक्के की ऊँचाई (h) = 2 mm = 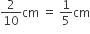
चाँदी के प्रत्येक सिक्के का आयतन = 
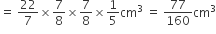
अत: घनाभ के लिए आवश्यक
चाँदी के सिक्कों की संख्या = 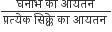
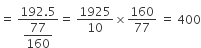
32 cm ऊँची और आधार त्रिज्या 18cm वाली एक बेलनाकार बाल्टी रेत से भरी हुई है। इस बाल्टी को भूमि पर खाली किया जाता है और इस रेत की एक शंक्वाकार ढेरी बनाई जाती है। यदि शंक्वाकार ढेरी की ऊँचाई 24cm है, तो इस ढेरी की त्रिज्या और तिर्यक ऊँचाई ज्ञात कीजिए।
यहाँ पर,
दी गई बेलनाकार बाल्टी के आधार की त्रिज्या (R) = 18 cm
दी गई बेलनाकार बाल्टी की ऊँचाई (H) = 32 cm
दी गई बेलनाकार बाल्टी के रेत का आयतन = 
= 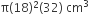
माना,
बाल्टी को खाली करने से बनी शंक्वाकार रेत की ढेरी की त्रिज्या = r cm
बाल्टी को खाली करने से बनी शंक्वाकार रेत की ढेरी की ऊँचाई (h) = 24 cm
बाल्टी को खाली करने से बनी शंक्वाकार रेत की ढेरी का आयतन = 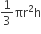
प्रश्नानुसार, 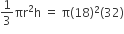

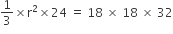

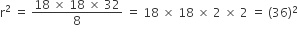
r = 36 cm
अब रेत की ढेरी की तिर्यक ऊँचाई (l) = 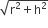
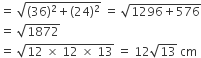
अत: रेत की ढेरी की त्रिज्या 36cm तथा तिर्यक ऊँचाई 
6m चौड़ी और 1.5 m गहरी एक नहर में पानी 10km/h की चाल से बह रहा है। 30 मिनट में, यह नहर कितने क्षेत्रफल की सिंचाई कर पाएगी, जबकि सिंचाई के लिए 8cm गहरे पानी की आवश्यकता होती है।
यहाँ पर,
नहर में पानी की चाल (l) = 10 km/h = 
नहर की चौड़ाई (b) = 6 m
नहर की गहराई (h) = 1.5 m
30 मिनट में नहर से निकले पानी का आयतन = 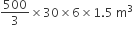

सिंचाई वाले क्षेत्र में पानी की ऊँचाई = 8 cm = 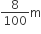
अत: सिंचाई वाले क्षेत्र का क्षेत्रफल = 
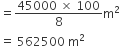
एक किसान अपने खेत में बनी 10 m व्यास वाली और 2m गहरी एक बेलनाकार टंकी को आंतरिक व्यास 20cm वाले एक पाइप द्वारा एक नहर से जोड़ता है। यदि पाइप में पानी 3km/h की चाल से बह रहा है, तो कितने समय बाद टंकी पूरी भर जाएगी?
यहाँ पर,
दी गई बेलनाकार टंकी का व्यास = 10 m
दी गई बेलनाकार टंकी की त्रिज्या (R) = 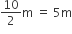
दी गई बेलनाकार टंकी की गहराई (H) = 2 m
दी गई बेलनाकार टंकी का आयतन = 
= 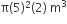

पाइप से निकलने वाले पानी की चाल = 3 km/h

माना पाइप द्वारा बेलनाकार टंकी को भरने में लगा समय = t min
दिए गए पाइप का आंतरिक व्यास = 20 cm = 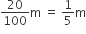
दिए गए पाइप की आंतरिक त्रिज्या (r) = 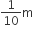
अत: दिए गए पाइप से t min निकलने वाले पानी का आयतन = 
= 
प्रश्नानुसार, 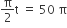
 t = 50 x 2 = 100
t = 50 x 2 = 100
अत: पाइप द्वारा बेलनाकार टंकी को भरने में लगा समय = 100 मिनट
पानी पीने वाला एक गिलास 14cm ऊँचाई वाले एक शंकु के छिन्नक के आकर का है। दोनों वृत्ताकार सिरों के व्यास 4cm और 2cm हैं। इस गिलास की धारिता ज्ञात कीजिए।
यहाँ पर, शंकु के छिन्नक के आकार के गिलास के लिए
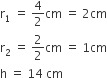
अत: गिलास की धारिता = 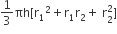
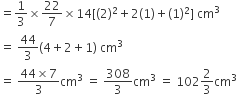
एक शंकु के छिन्नक की तिर्यक ऊँचाई 4cm है तथा इसके वृत्तीय सिरों के परिमाप (परिधियाँ) 18cm और 6cm हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
यहाँ पर , शंकु के छिन्नक के लिए ऊपरी सिरे की परिधि = 18 cm
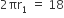

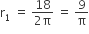 cm
cm
निचले सिरे की परिधि = 6cm




तिर्यक ऊँचाई (l) = 4 cm
अत: शंकु के छिन्नक का वक्र पृष्ठीय क्षेत्रफल = 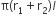
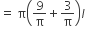
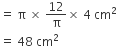
एक तुर्की टोपी शंकु के एक छिन्नक के आकर की है। यदि इसके खुले सिरे की त्रिज्या 10cm है, ऊपरी सिरे की त्रिज्या 4cm है और टोपी की तिर्यक ऊँचाई 15cm है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए। 
यहाँ पर, शंकु के छिन्नक के आकर की तुर्की टोपी के लिए
r1 = 10cm
r2 = 4 cm
l = 15 cm
अत: टोपी को बनाने में प्रयुक्त पदार्थ का क्षेत्रफल = 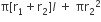
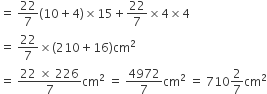
धातु की चादर से बना और ऊपर से खुला एक बर्तन शंकु के एक छिन्नक के आकर का है, जिसकी ऊँचाई 16cm है तथा निचले और ऊपरी सिरों की त्रिज्याएँ क्रमश: 8cm और 20cm हैं। 20रु प्रति लीटर की दर से, इस बर्तन को पूरा भर सकने वाले दूध का मूल्य ज्ञात कीजिए। साथ ही, इस बर्तन को बनाने के लिए प्रयुक्त धातु की चादर का मूल्य 8रु प्रति 100 cm2 की दर से ज्ञात कीजिए।
यहाँ पर, शंकु के छिन्नक के आकार के बर्तन के लिए
r1 = 20cm
r2 = 8 cm
h = 16 cm
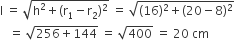
बर्तन को बनाने में प्रयुक्त धातु की चादर का क्षेत्रफल = 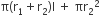
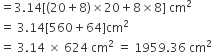
100 cm2 धातु की चादर का मूल्य = 8 रु
1cm2 धातु की चादर का मूल्य = 
1959.36 cm2 धातु की चादर का मूल्य = 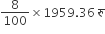
= 156.75 रु
बर्तन में उपस्थित दूध का आयतन = 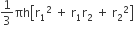
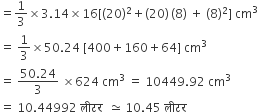
बर्तन में उपस्थित 1 लीटर दूध का मूल्य = 20 रु
बर्तन में उपस्थित 10.45 लीटर दूध का मूल्य = 10.45 x 20 रु
= 209 रु
20 cm ऊँचाई और शीर्ष कोण (vertical angle) 60° वाले एक शंकु को उसकी ऊँचाई के बीचो-बीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समांतर है। यदि इस प्राप्त शंकु के छिन्नक को व्यास 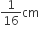 वाले एक तार के रूप में बदल दिया जाता है तो तार की लंबाई ज्ञात कीजिए।
वाले एक तार के रूप में बदल दिया जाता है तो तार की लंबाई ज्ञात कीजिए।
माना APQ एक दिया गया शंकु है, जिसका शीर्ष  तथा ऊँचाई 20cm है।
तथा ऊँचाई 20cm है।
इसे बिंदु O' से इस प्रकार काटा गया है कि AO' = O'O है।
माना शंकु के छिन्नक PQQ'P के वृत्ताकार सिरों की त्रिज्याएँ r1 तथा r2 हैं तो  तथा
तथा  में,
में,
 व
व 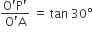
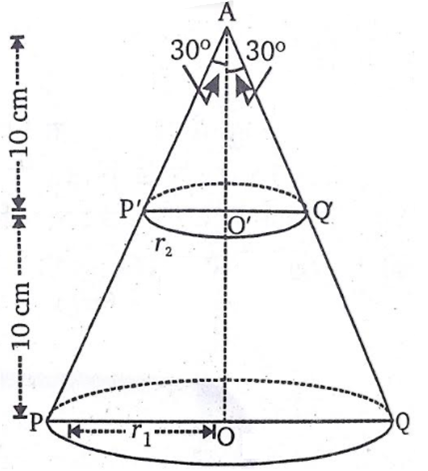

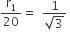 व
व 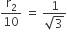

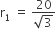 व
व 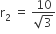
शंकु के छिन्नक का आयतन = 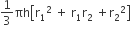
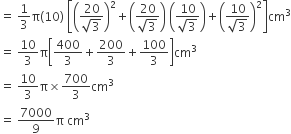
माना शंकु के छिन्नक से बने बेलनाकार तार की लंबाई = h cm
दिया है शंकु के छिन्नक से बने बेलनाकार तार का व्यास = 
अत: शंकु के छिन्नक से बने बेलनाकार तार की त्रिज्या (r) = 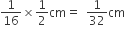
शंकु के छिन्नक से बने बेलनाकार तार का आयतन = 
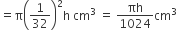
प्रश्नानुसार, 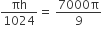

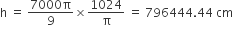
= 7964.44 m
अत: शंकु के छिन्नक से बने बेलनाकार तार की लंबाई = 7964.44 m
व्यास 3mm वाले ताँबें के एक तारे को 12cm लंबे और 10cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतया ढक लेता है। तार की लंबाई और दर्व्यमान ज्ञात कीजिए, यह मानते हुए की ताँबे का घनत्व 8.88g प्रति cm3 है।
यहाँ पर, प्रश्नानुसार स्पष्ट होता है कि
बेलन पर तार को एक बार लपेट देने पर उसकी लम्बाई का 3mm(0.3 cm) भाग ढक जाता है।
∴ बेलन की पूरी लंबाई ढकने के लिए आवश्यक लपेटों की संख्या = 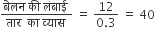
क्योंकि एक लपेट में तार की लंबाई बेलन के सिरे की परिधि के बराबर है
अब बेलन की त्रिज्या (r) = 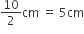
बेलन की परिधि = 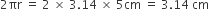
40 लपेटों में लगी तार की लंबाई (h) = 40 x 3.14 = 1256 cm
ताँबें की तार की त्रिज्या (r1) = 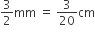
ताँबें की तार का आयतन = 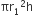
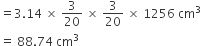
1 cm3 ताँबें की तार का द्रव्यमान = 8.88 g
88.74 cm3 ताँबें की तार का द्रव्यमान = 88.74 x 8.88g = 788 g(लगभग)
एक समकोण त्रिभुज, जिसकी भुजाएँ 3cm और 4cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परित: घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। ( का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
माना,
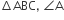 पर समकोण हैं
पर समकोण हैं
जिसमें AB = 3 cm
AC = 4 cm
तो कर्ण (BC) = 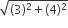
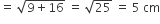
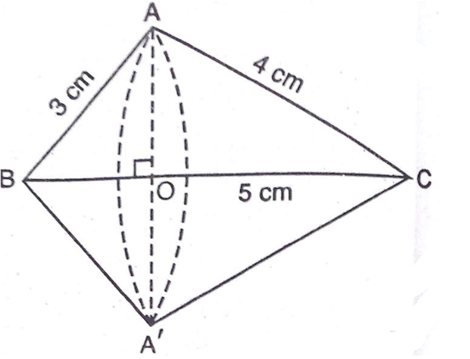
समकोण त्रिभुज को कर्ण BC के गिर्द घुमाने पर बने द्विशंकु के उभयनिष्ठ आधार की त्रिज्या AO या A'O है।
शंकु BAA' की ऊँचाई BO तथा तिर्यक ऊँचाई 3cm है।
शंकु CAA' की ऊँचाई CO तथा तिर्यक ऊँचाई 4cm है।
समकोण त्रिभुजों AOB तथा BAC में,
 (उभयनिष्ठ)
(उभयनिष्ठ)
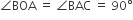
इसलिए,  तथा
तथा  समरूप हैं।
समरूप हैं। 
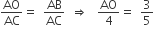

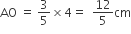
तथा 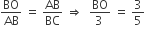

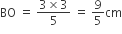
अब, 
शंकु BAA' का आयतन = 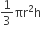
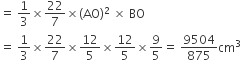
शंकु CAA' का आयतन = 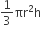
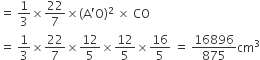
 द्विशंकु का आयतन =
द्विशंकु का आयतन = 
इस प्रकार
द्विशंकु का पृष्ठीय क्षेत्रफल = शंकु (BAA' + CAA') का पृष्ठीय क्षेत्रफल
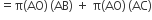
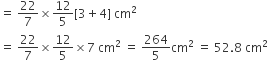
एक टंकी, जिसके आंतरिक मापन 150cm x 120cm x 110 cm हैं, में 129600 cm3 पानी है। इस पानी में कुछ छिद्र वाली ईंटें तब तक डाली जाती हैं, जब तक की टंकी पूरी ऊपर तक भर न जाए। प्रत्येक ईंट अपने आयतन का  पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm x 7.5cm x 6.5cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे?
पानी सोख लेती है। यदि प्रत्येक ईंट की माप 22.5 cm x 7.5cm x 6.5cm हैं, तो टंकी में कुल कितनी ईंटें डाली जा सकती हैं, ताकि उसमें से पानी बाहर न बहे?
यहाँ पर,
दी गई टंकी का आयतन = 150 x 120 x 110 cm3
= 1980000 cm3
दी गई टंकी में उपस्थित पानी का आयतन = 129600 cm3
दी गई प्रत्येक ईंट का आयतन = 22.5 x 7.5 x 6.5 cm3
= 1096.875 cm3
माना टंकी में डाली जा सकने वाली ईंटों की संख्या = n
तो n ईंटों द्वारा सोखो जाने वाले पानी का आयतन = n x 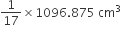
= 64.522 n cm3' टंकी में शेष बचे पानी का आयतन = [129600 - 64.522 n] cm3
टंकी में शेष बचे पानी का आयतन = [129600 - 64.522 n] cm3
प्रश्नानुसार,
टंकी में शेष बचे पानी का आयतन + n ईंटों का आयतन = टंकी का आयतन
 [1096.875 - 64.522]n = 1980000 - 129600
[1096.875 - 64.522]n = 1980000 - 129600
 1032.353 n = 1850400
1032.353 n = 1850400

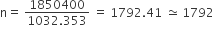
अत: आवश्यक ईंटों की संख्या = 1792
किसी महीने के 15 दिनों में, एक नदी की घाटी में वर्षा हुई। यदि इस घाटी का क्षेत्रफल है, तो दर्शाइए कि कुल वर्षा लगभग तीन नदियों के सामान्य पानी के योग के समतुल्य थी, जबकि प्रत्येक नदी 1072 km लम्बी, 75 m चौड़ी और 3m गहरी है।
यहाँ पर,
दी गई घाटी का क्षेत्रफल = 7280 km2
= 7280 x 1000 x 1000 m2 = 7280000000 m2
घाटी में 15 दिनों में हुई वर्षा से ऊँचाई (h) = 10cm = 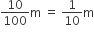
घाटी में हुई वर्षा का कुल आयतन = क्षेत्रफल x ऊँचाई
= 7280000000 x 
दी गई प्रत्येक नदी की लंबाई (l) = 1072 km = 1072000 m
दी गई प्रत्येक नदी की चौड़ाई (b) = 75m
दी गई प्रत्येक नदी की गहराई (h) = 3 m
दी गई प्रत्येक नदी का आयतन = l x b x h
= 1072000 x 75 x 3m3
= 241200000 m3
तीनों नदियों में समा सकने वाले जल का आयतन = 3 x 241200000 m3
= 723600000 m3
अत: घाटी में हुई वर्षा का आयतन तीनों नदियों में समा सकने वाले जल के आयतन के लगभग बराबर है।
टीन की बनी हुई एक तेल की कुप्पी 10 cm लंबे एक बेलन में एक शंकु के छिन्नक को जोड़ने से बनी है। यदि इसकी कुल ऊँचाई 22 cm है, बेलनाकार भाग का व्यास 8cm है और कुप्पी के ऊपरी सिरे का व्यास 18 cm है, तो इसके बनाने में लगी टीम की चादर का क्षेत्रफल ज्ञात कीजिए।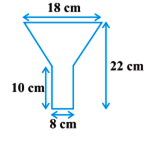
यहाँ पर,
कुप्पी के बेलनाकार भाग का व्यास = 8 cm
कुप्पी के बेलनाकार भाग की त्रिज्या (r1) = 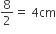
कुप्पी के बेलनाकार भाग की ऊँचाई (h1) = 10 cm
कुप्पी के बेलनाकार भाग का पृष्ठीय क्षेत्रफल = 
= 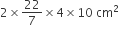
= 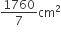
कुप्पी के शंकु रूपी छिन्नक वाले भाग के लिए,
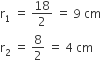
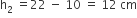
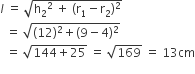
पृष्ठीय क्षेत्रफल = 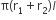
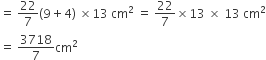
अत: कीप को बनाने में लगी टीम की चादर का कुल पृष्ठीय क्षेत्रफल
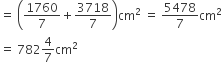
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किए संकेतों का प्रयोग करते हुए, वक्र पृष्ठीय क्षेत्रफल और सम्पूर्ण पृष्ठीय क्षेत्रफल के निम्न सूत्रों को सिद्ध कीजिए,
(i) वक्र पृष्ठीय क्षेत्रफल = 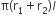
(ii) सम्पूर्ण पृष्ठीय क्षेत्रफल = 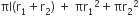
माना ABB1A1 छिन्नक की ऊँचाई h, तिर्यक ऊँचाई l तथा वृत्ताकार आधारों की त्रिज्याएँ r1 व r2 हैं।
जहाँ (r1 > r2)
माना शंकु VAB में, तिर्यक ऊँचाई (VA) = l1
ऊँचाई (VO) = h1
तो शंकु VA1B1 में,
तिर्यक ऊँचाई (VA1) = l1 - l
ऊँचाई (VO1) = h1 - h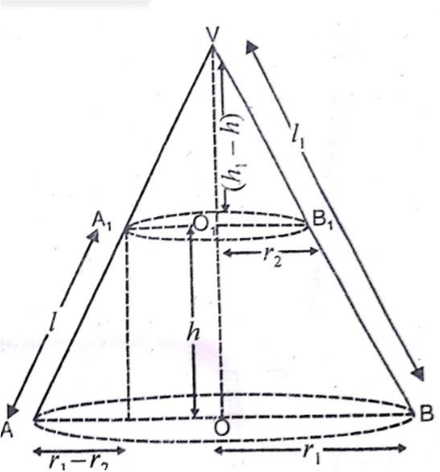
क्योंकि समकोण  व
व  समरूप हैं।
समरूप हैं।


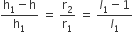

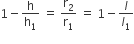

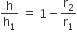 व
व 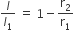

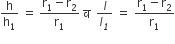

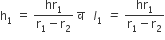 ...(i)
...(i)
अब, शंकु  की ऊँचाई = h1 - h
की ऊँचाई = h1 - h
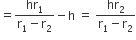 ...(ii)
...(ii)
शंकु VA1B1 की तिर्यक ऊँचाई = 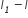
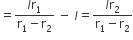 ...(iii)
...(iii)
(i) छिन्नक का वक्र पृष्ठीय क्षेत्रफल = (शंकु VAB - शंकु VA1B1) का एक वक्र पृष्ठीय क्षेत्रफल
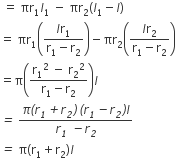
(ii) छिन्नक का सम्पूर्ण पृष्ठीय क्षेत्रफल = छिन्नक का वक्र पृष्ठीय क्षेत्रफल + (नीचे वाले वृत्ताकार आधार + ऊपरी वृत्ताकार शीर्ष) का क्षेत्रफल
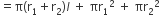
शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किये संकेतों का प्रयोग करते हुए, आयतन का निम्न सूत्र सिद्ध कीजिए
आयतन = 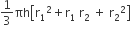
माना ABB1A1 छिन्नक की ऊँचाई h, तिर्यक ऊँचाई l तथा वृत्ताकार आधारों की त्रिज्याएँ r1 व r2 हैं
(जहाँ r1 > r2)।
माना शंकु VAB में, तिर्यक ऊँचाई (VA) = l1
ऊँचाई (VO) = h1
तो शंकु VA1B1 में,
तिर्यक ऊँचाई (VA1) = l1 - l
ऊँचाई (VO1) = h1 - h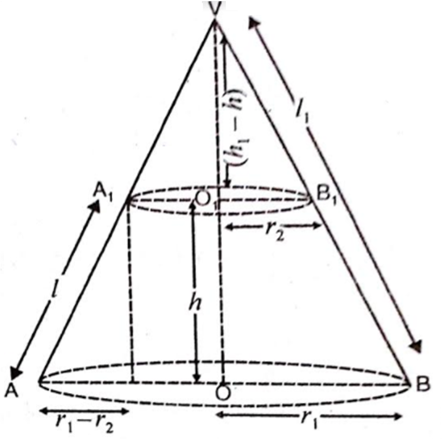
क्योंकि समकोण  व
व 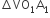 समरूप है।
समरूप है।


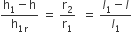

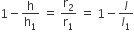


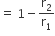

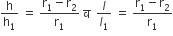

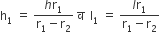 ...(i)
...(i)
अब, शंकु VA1B1 की ऊँचाई = h1 - h
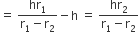 ...(ii)
...(ii)
शंकु VA1B1 की तिर्यक ऊँचाई = l1 - l
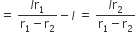 ...(iii)
...(iii)
छिन्नक का आयतन = (शंकु VAB - शंकु VA1B1) का आयतन
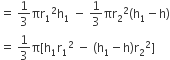
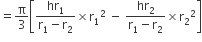 [समीकरण (i) व (ii) से]
[समीकरण (i) व (ii) से]
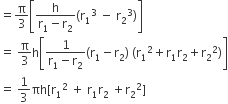
एक कलमदान घनाभ के आकर की एक लकड़ी से बना है जिसमें कलम रखने के लिए चार शंक्वाकार गड्ढे बने हुए हैं। घनाभ की विमाएँ 15cm x 10cm x 3.5cm हैं। प्रत्येक गड्ढे की त्रिज्या 0.5 cm और गहराई 1.4 cm है। पूरे कलमदान में लकड़ी का आयतन ज्ञात कीजिए।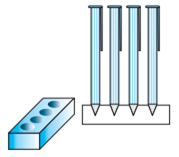
यहाँ पर,
घनाभाकर लकड़ी का कुल आयतन = (15 x 10 x 3.5) cm3
= 525 cm3
कलमदान के प्रत्येक शंक्वाकार गड्ढे की त्रिज्या (r) = 0.5 cm
कलमदान के प्रत्येक शंक्वाकार गड्ढे की गहराई (h) = 1.4 cm
कलमदान के चारों शंक्वाकार गड्ढों का आयतन = 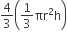
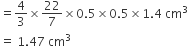
अतः कलमदान की लकड़ी की आयतन = (घनाभाकर लकड़ी - शंक्वाकार गड्ढों) का आयतन
= (525 - 1.47) cm3
= 525.53 cm3
4 मी व्यास का एक कुआँ, 21 मी की गहराई तक खोदा जाता है। इससे निकली हुई मिट्टी को कुएँ के चारों ओर 3 मी चौड़ी एक वृत्ताकार वलय (ring) बनाते हुए समान रूप से फैला कर एक बॉँध बनाया जाता है। बाँध की ऊँचाई ज्ञात कीजिए।
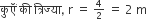
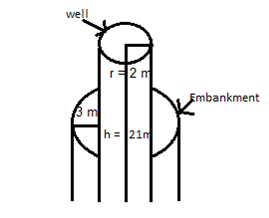
परिधि की त्रिज्या, R = 2 + 3 = 5 m
कुऍं की ऊँचाई, h = 21 m
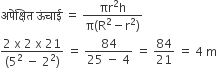
सिध्द हुआ, कि परिधि की ऊँचाई 4m है।
Sponsor Area
एक ठोस लंब वृत्तीय बेलन के आधार की त्रिज्या तथा ऊँचाई का योग 37 सेमी है। यदि ठोस का कुल पृष्ठीय क्षेत्रफल 1628 वर्ग सेमी है, तो ठोस बेलन का आयतन ज्ञात कीजिए। 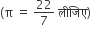
माना बेलन की त्रिज्या (r) और ऊँचाई (h) है।
= r + h = 37 cm ..........(i)
बेलन की कुल सतह का क्षेत्रफल = 1628 cm2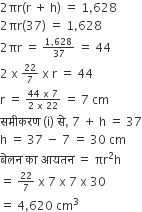
ऊपर से खुली एक बाल्टी शंकु के छिन्नक के आकर की है जिसकी धरिका 12308.8 सेमी3 की है। उसके ऊपरी तथा निचले वृतीय सिरों की त्रिज्याएँ क्रमशः 20 सेमी तथा 12 सेमी हैं। बाल्टी की ऊँचाई ज्ञात कीजिए
तथा बाल्टी को बनाने में लगी धातु की चादर का क्षेत्रफल ज्ञात कीजिए। 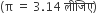
बाल्टी के शीर्ष की त्रिज्या, R = 20 सेमी
बाल्टी के नीचे की त्रिज्या, r = 20 सेमी
बाल्टी का आयतन = 12308.8 cm3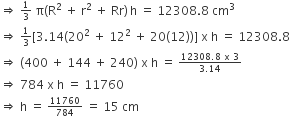
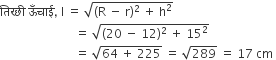
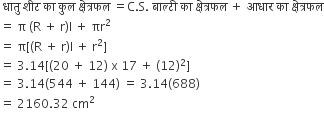
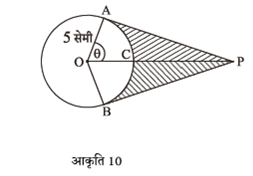
5 सेमी आंतरिक त्रिज्या तथा 24 सेमी ऊँचाई के एक शंक्वाकार बर्तन का  भाग पानी से भरा है। इस पानी को 10 सेमी आंतरिक त्रिज्या के बेलनाकार बर्तन में खाली किया जाता है। बेलनाकार बर्तनों में पानी की ऊँचाई ज्ञात कीजिए।
भाग पानी से भरा है। इस पानी को 10 सेमी आंतरिक त्रिज्या के बेलनाकार बर्तन में खाली किया जाता है। बेलनाकार बर्तनों में पानी की ऊँचाई ज्ञात कीजिए।
शंक्वाकार पोत की त्रिज्या = 5 सेमी
शंक्वाकार पोत की ऊंचाई h = 24 सेमी
शंक्वाकार पोत के पानी की मात्रा =  × मात्रा।
× मात्रा।
माना h, बेलनाकार पोत की ऊँचाई है। जो शंक्वाकार पोत के पानी से भरा हुआ है,
बेलनाकार पोत का त्रिज्या = 10 सेमी
स्पष्ट रूप से,
बेलनाकार पोत का आयतन = पानी की मात्रा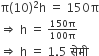
इस प्रकार, बेलनाकार पोत की ऊँचाई 1.5 सेमी है।
आकृति-1 में, ABCD एक आयत है । x तथा y के मान ज्ञात कीजिए।

आयता ABCD में
DC = AB और BC = AD
x + y = 30 ...(i)
और
x -y = 14 ...(ii)
समीकरण (i) और (ii), जोड़ने पर
2x = 44
x = 22
समीकरण (i) में x का मान रखने पर
x + y = 30
22 + y = 30
y = 30-22
y = 8
इसलिए, x = 22 and y = 8
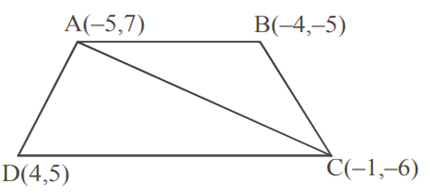
यदि A(-5, 7), B(-4, -5), C-1,-6) तथा D(4, 5) एक चतुर्भुज ABCD के शीर्ष बिंदु हैं, तो चतुर्भुज ABCD का क्षेत्रफल ज्ञात कीजिए।
M, AC और BD का मध्य बिंदु है, मध्य बिंदु सूत्र का उपयोग
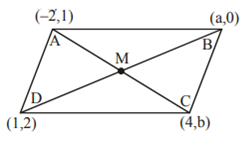
लकड़ी के एक बेलन के प्रत्येक सिरे पर एक अर्थ गोला खोदकर निकालते हुए, एक वस्तु बनाई गई जैसा की आकृति में दर्शाया गया है यदि बेलन की ऊंचाई 10 सेंटीमीटर है, आधार की त्रिज्या 3. 5 सेंटीमीटर है तो इस वस्तु का संपूर्ण पृष्ठीय क्षेत्रफल ज्ञात कीजिए

r सिलेंडर के आधार की त्रिज्या है और इसकी ऊंचाई h है। फिर, लेख का कुल सतह क्षेत्र = सिलेंडर + 2 (गोलार्ध के सतह क्षेत्र) के घुमावदार सतह क्षेत्र

चावल कि एक ढेरी शंकु के आकार की है, जिसके आधार का व्यास 24 मीटर तथा ऊंचाई 3.5 मीटर है। चावलों का आयतन ज्ञात कीजिए एक बेरी को पूरा-पूरा ढकने के लिए कितने कैनवस की आवश्यकता है।
आधार व्यास = 24 m
आधार त्रिज्या = 12 m
ऊंचाई = 3.5
शंकु के छिन्नक के आकार की एक बाल्टी के निचले तथा ऊपरी किनारों के व्यास क्रमशः 10 सेंटीमीटर तथा 30 सेंटीमीटर है। यदि भारती की ऊंचाई 24 सेंटीमीटर है तो ज्ञात कीजिए।
(i) बाल्टी को बनाने में लगने वाली धातु की सीट का क्षेत्रफल।
(ii) बाल्टी बनाने में सामान्य प्लास्टिक को क्यों नहीं लगाना चाहिए। [π =3.14 ]
माना r1 = 5 cm और r2 = 15cm निचले और ऊपरी परिपत्र की त्रिज्या हैं।
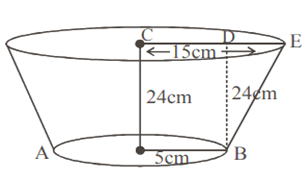
AB = CD = 5 cm
DE = 15 – 5 = 10 cm
and BD = 24 cm
∴ BE2 = BD2 + DE2
= 576 + 100
BE2 = 676
BE = 26 cm =l
बाल्टी को बनाने में लगने वाली धातु की सीट का क्षेत्रफल
(ii) बाल्टी बनाने में सामान्य प्लास्टिक को इसलिए नहीं लगाना चाहिए क्यूँकि एक साधारण प्लास्टिक तनाव के कारण आसानी से टूट सकती है।
आकृति में छायांकित भाग का क्षेत्रफल ज्ञात कीजिए । जहाँ वर्ग ABCD के शी A, B, C तथा D को केन्द्र मान कर खींची गई चापें भुजाओं AB, BC, CD तथा DA के मध्य बिंदुओं क्रमशः P, Q, R तथा S पर दो-दो के जोड़ों में काटती है तथा वर्ग की भुजा 12 सेमी है । [π = 3.14 लीजिए]

ABCD एक वर्ग है जिसमें P, Q, R, S पक्ष AB, BC CD तथा DA के मध्य बिंदु है
AB cm = 12 cm
⇒ AP = 6 cm { P भुजा AB को दो भागों में बांटती}
छायांकित भाग का क्षेत्रफल = ABCD वर्ग का क्षेत्रफल - ( APEC क्षेत्र का क्षेत्रफल + PFEQ क्षेत्र का क्षेत्रफल + RGQC क्षेत्र का क्षेत्रफल + RHSD क्षेत्र का क्षेत्रफल)

Mock Test Series
Sponsor Area
Sponsor Area