व्यास 3mm वाले ताँबें के एक तारे को 12cm लंबे और 10cm व्यास वाले एक बेलन पर इस प्रकार लपेटा जाता है कि वह बेलन के वक्र पृष्ठ को पूर्णतया ढक लेता है। तार की लंबाई और दर्व्यमान ज्ञात कीजिए, यह मानते हुए की ताँबे का घनत्व 8.88g प्रति cm3 है।
यहाँ पर, प्रश्नानुसार स्पष्ट होता है कि
बेलन पर तार को एक बार लपेट देने पर उसकी लम्बाई का 3mm(0.3 cm) भाग ढक जाता है।
∴ बेलन की पूरी लंबाई ढकने के लिए आवश्यक लपेटों की संख्या = 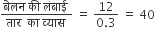
क्योंकि एक लपेट में तार की लंबाई बेलन के सिरे की परिधि के बराबर है
अब बेलन की त्रिज्या (r) = 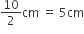
बेलन की परिधि = 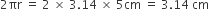
40 लपेटों में लगी तार की लंबाई (h) = 40 x 3.14 = 1256 cm
ताँबें की तार की त्रिज्या (r1) = 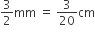
ताँबें की तार का आयतन = 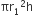
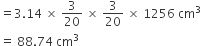
1 cm3 ताँबें की तार का द्रव्यमान = 8.88 g
88.74 cm3 ताँबें की तार का द्रव्यमान = 88.74 x 8.88g = 788 g(लगभग)



