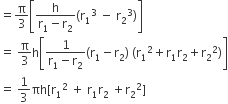शंकु के एक छिन्नक के लिए, पूर्व स्पष्ट किये संकेतों का प्रयोग करते हुए, आयतन का निम्न सूत्र सिद्ध कीजिए
आयतन  =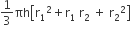 
  

माना ABB₁A₁ छिन्नक की ऊँचाई h, तिर्यक ऊँचाई l तथा वृत्ताकार आधारों की त्रिज्याएँ r₁ व r₂ हैं 
(जहाँ r₁ > r₂)।
माना शंकु VAB में,    तिर्यक ऊँचाई (VA) = l₁
                          ऊँचाई (VO) = h₁
तो शंकु VA₁B₁ में,
                       तिर्यक ऊँचाई (VA₁) = l₁ - l
                          ऊँचाई (VO₁) = h₁ - h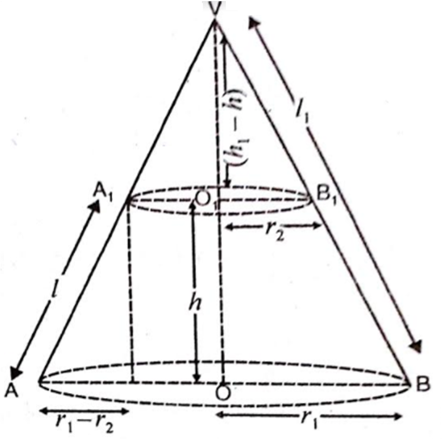

क्योंकि समकोण  व 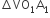 समरूप है।
                               
               
               
                       
                                   
                           
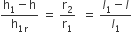
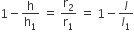
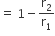
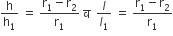
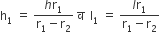                                   ...(i)
अब,   शंकु VA₁B₁  की ऊँचाई = h₁ - h
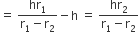                                                 ...(ii)
शंकु VA₁B₁  की तिर्यक ऊँचाई  = l₁ - l
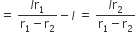                                                  ...(iii)
छिन्नक का आयतन  = (शंकु VAB - शंकु VA₁B₁) का आयतन
                         
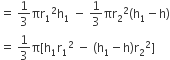
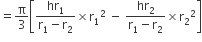                          [समीकरण (i) व (ii) से]