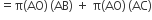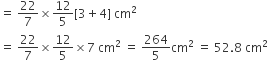एक समकोण त्रिभुज, जिसकी भुजाएँ 3cm और 4cm हैं (कर्ण के अतिरिक्त), को उसके कर्ण के परित: घुमाया जाता है। इस प्रकार प्राप्त द्वि-शंकु (double cone) के आयतन और पृष्ठीय क्षेत्रफल ज्ञात कीजिए। (
का मान जो भी उपयुक्त लगे, प्रयोग कीजिए।)
माना,
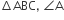पर समकोण हैं
जिसमें AB = 3 cm
AC = 4 cm
तो कर्ण (BC) =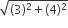 
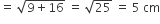
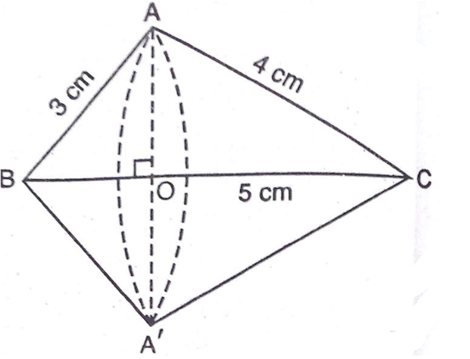
समकोण त्रिभुज को कर्ण BC के गिर्द घुमाने पर बने द्विशंकु के उभयनिष्ठ आधार की त्रिज्या AO या A'O है।
शंकु BAA' की ऊँचाई BO तथा तिर्यक ऊँचाई 3cm है।
शंकु CAA' की ऊँचाई CO तथा तिर्यक ऊँचाई 4cm है।
समकोण त्रिभुजों AOB तथा BAC में,
(उभयनिष्ठ)
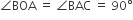
इसलिए, 
तथा 
समरूप हैं। 
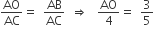
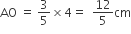
तथा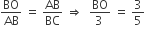 
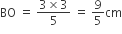
अब, 
शंकु BAA' का आयतन =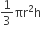 
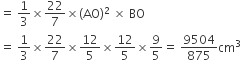
शंकु CAA' का आयतन =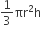 
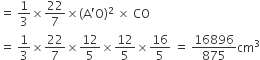
द्विशंकु का आयतन = 
इस प्रकार
द्विशंकु का पृष्ठीय क्षेत्रफल = शंकु (BAA' + CAA') का पृष्ठीय क्षेत्रफल
