एक ठोस में, ऊँचाई 120cm और त्रिज्या 60cm वाला एक शंकु सम्मलित है, जो 60cm त्रिज्या वाले एक अर्धगोले पर आरोपित है। इस ठोस को पानी से भरे हुए एक लम्ब वृत्तीय बेलन में इस प्रकार सीधा डाल दिया जाता है कि यह बेलन की तली को स्पर्श करे। यदि बेलन की त्रिज्या 60cm है और ऊँचाई 180 cm है तो बेलन में शेष बचे पानी का आयतन ज्ञात कीजिए।
यहाँ पर,
लंब वृत्तीय बेलनाकार बर्तन की त्रिज्या (R) = 60 cm
लंब वृत्तीय बेलनाकार बर्तन की ऊँचाई (H) = 180 cm
लंब वृत्तीय बेलनाकार बर्तन की आयतन (V1) = 
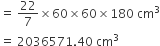
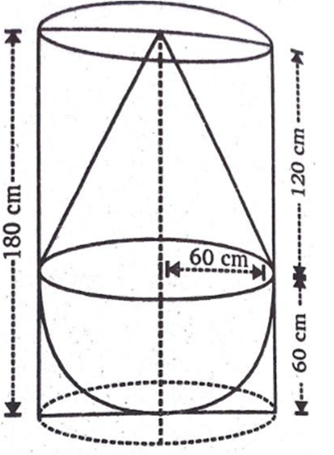
ठोस के शंक्वाकार भाग की त्रिज्या (r) = अर्धगोलाकार भाग की त्रिज्या
(r) = 60 cm
ठोस के शंक्वाकार भाग की ऊँचाई (h) = 120 cm
ठोस का आयतन (V2) = (शंक्वाकार भाग + अर्धगोलाकार भाग) का आयतन
= 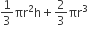
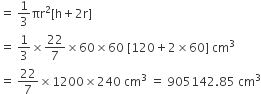
अत: बेलनाकार बर्तन में शेष बचे पानी की आयतन = V1 - V2
= (2036571.40 - 905142.85)cm3
= 1131428.55 cm3
= 1.131 m3 (लगभग)



