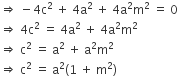गणित Chapter 4 द्विघात समीकरण
Sponsor Area
NCERT Solution For Class 10 गणित गणित
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
(x + 1)2 = 2(x – 3)
बायाँ पक्ष = (x + 1)2 = x2 + 2x + 1
दायाँ पक्ष = 2(x – 3) = 2x – 6
∴ 6x2 + 2x + 1 = 2x - 6
⇒ x2 + 2x + 1 – 2x + 6 = 0
⇒ x2+ 7 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में है, जहाँ a = 1, b = 0, c = 7
अत: दिया हुआ समीकरण द्विघात समीकरण है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
x2 – 2x = ( – 2 ) ( 3 – x )
दायाँ पक्ष = ( – 2 ) ( 3 – x ) = – 6 + 2x
∴ x2 – 2x = – 6 + 2x
⇒ x2 – 2x + 6 – 2x = 0
⇒ x2 – 4x + 6 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में है, जहाँ = 1, b = – 4, c = 6
अत: दिया हुआ समीकरण द्विघात समीकरण है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
(x – 2) (x + 1) = (x – 1) (x + 3)
बायाँ पक्ष = (x – 2) (x + 1)
= x2 - 2x + x - 2
= x2 – x – 2
दायाँ पक्ष = (x – 1) (x + 3)
= x2 + 2x – 3
∴ x2 – x – 2 = x2 + 2x – 3
⇒ – x – 2 – 2x + 3 = 0
⇒ – 3x + 1 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में नहीं है
अत: दिया हुआ समीकरण द्विघात समीकरण नहीं है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
(x – 3) (2x + 1) = x(x + 5)
बायाँ पक्ष = (x – 1) (2x + 1)
= 2x2 + x – 2x – 1
= 2x2 – x – 1
बायाँ पक्ष = x(x + 5) = x2 + 5x
∴ 2x2 – x – 1 = x2 + 5x
⇒ 2x2 – x2 – x – 5x – 1 = 0
⇒ x2 – 6x – 1 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में है, जहाँ a = 1, b = – 6, c = – 1
अत: दिया हुआ समीकरण द्विघात समीकरण है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
(2x – 1) (x – 3) = (x + 5)(x – 1)
बायाँ पक्ष = (2x – 1) (x – 3)
= 2x2 – 6x – x + 3
= 2x2 – 7x + 3
दायाँ पक्ष = (x + 5) (x – 1)
= x2 + 5x – x – 5
= x2 + 4x – 5
∴ 2x2 – 7x + 3 = x2 + 4x – 5
⇒ 2x2 – x2 - 7x – 4x + 3 + 5 = 0
⇒ x2 – 11x + 8 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में है, जहाँ a = 1, b = – 11, c = 8
अत: दिया हुआ समीकरण द्विघात समीकरण है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
x2 + 3x + 1 = (x – 2)2
दायाँ पक्ष = (x – 2)2 = x2 – 4x + 4
∴ x2 + 3x + 1 = x2 – 4x + 4
⇒ 3x + 4x + 1 – 4 = 0
⇒ 7x – 3 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में नहीं हैं
अत: दिया हुआ समीकरण द्विघात समीकरण नहीं है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
(x + 2)3 = 2x (x2 – 1)
बायाँ पक्ष = (x + 2)3
= x3 + 3x2.2 + 3x.( 2 )2 + 8
= x3 + 6x2 + 12x + 8
दायाँ पक्ष = 2x(x2 – 1) = 2x3 – 2x
∴ x3 + 6x2 + 12x + 8 = 2x3 - 2x
⇒ x3 – 2x3 + 6x2 + 12x + 2x + 8 = 0
⇒ – x3 + 6x2 + 14x + 8 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में नहीं है
अत: दिया हुआ समीकरण द्विघात समीकरण नहीं है।
जाँच कीजिए कि क्या निम्न द्विघात समीकरण हैं:
x3 – 4x2 – x + 1 = (x – 2)3
दायाँ पक्ष = (x – 2)3
= x3 – 23 – 3x.2 (x – 2)
= x3 – 8 – 6x2 + 12x
= a3 – 6x2 + 12x – 8
∴ x3 – 4x2 – x + 1 = x3 – 6x2 + 12x – 8
⇒ – 4x2 + 6x2 – x – 12x + 1 + 8 = 0
⇒ 2x2– 13x + 9 = 0
∵ यह समीकरण ax2 + bx + c = 0 के रूप में है, जहाँ a = 2, b = – 13, c = 9
अत: दिया हुआ समीकरण द्विघात समीकरण है।
निम्न स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए:
एक आयताकार भूखंड का क्षेत्रफल 528 m2 है।क्षेत्र की लंबाई ( मीटरों में ) चौड़ाई के दुगुने से एक अधिक है। हमें भूखंड की लंबाई और चौड़ाई ज्ञात करनी है।
तो चौड़ाई = (2x + 1) m
∵ आयत का क्षेत्रफल = x (2x + 1) m2
प्रश्नानुसार,
(2x + 1)x = 528 ⇒ 2x2 + x – 528 = 0
जो की x के अभीष्ट एक द्विघात समीकरण हैं।
समीकरण को गुणनखंड विधि से हल करने पर
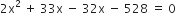

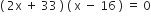

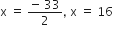
चौड़ाई ऋणात्मक नहीं हो सकती
∴ x = 16
अत: आयत की चौड़ाई = 16 m
आयत की लंबाई = 2 x 16 + 1 = 33 m
निम्न स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए:
दो क्रमागत धनात्मक पूर्णांकों का गुणनफल 306 है। हमें पूर्णांकों को ज्ञात करना हैं।
मन दो क्रमागत धनात्मक पूर्णांक x और (x + 1) हैं।
तो प्रश्नानुसार,
x(x + 1) = 306
⇒ x2 + x – 306 = 0
यह x के अभीष्ट एक द्विघात समीकरण हैं।
गुणनखंड विधि से हल करने पर
x2 + 18x – 17x – 306 = 0
⇒ x(x + 18) – 17(x + 18) = 0
⇒ (x + 18) (x – 17) = 0
⇒ x + 18 = 0, x – 17 = 0
⇒ x = –18, x = 17
क्योंकि पूर्णांक धनात्मक है इसलिए
∴ x = 17
अत: दो क्रमागत पूर्णांक 17 और 18 हैं।
निम्न स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए:
रोहन की माँ उससे 26 वर्ष बड़ी है। उनकी आयु ( वर्षों में ) का गुणनफल अब से तीन वर्ष पश्चात 360 हो जाएगी। हमें रोहन की वर्तमान आयु ज्ञात करनी हैं।
माना रोहन की वर्तमान आयु = x वर्ष
तो रोहन की माँ की आयु = (x + 26) वर्ष
3 वर्ष बाद
रोहन की आयु= (x + 3) वर्ष
रोहन की माँ की आयु = x + 26 + 3 = (x + 29) वर्ष
प्रश्नानुसार, (x + 3) (x + 29) = 360
⇒ x2 + 32x – 360 + 87 = 0
⇒ x2 + 32x – 273 = 0
⇒ x2 + 39x – 7x – 273 = 0
⇒ x(x + 39) – 7(x + 39) = 0
⇒ (x + 39) (x – 7) = 0
⇒ x = –39, x – 7 = 0 लेकिन आयु ऋणात्मक नहीं होती
∴ x = 17
अत: रोहन की वर्तमान आयु = 7 वर्ष
निम्न स्थितियों को द्विघात समीकरणों के रूप में निरूपित कीजिए:
एक रेलगाड़ी 480 km/h की दूरी समान चाल से तय करती है। यदि इसकी चाल 8 km/h कम होती, तो वह उसी दूरी को तय करने में 3 घंटे अधिक लेती। हमें रेलगाड़ी की चाल ज्ञात करनी है।
दूरी = 480 km
480 km दूरी तय करने में लगने वाला समय
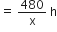
प्रश्नानुसार,
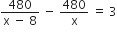
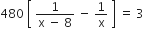

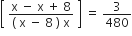
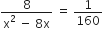
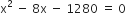
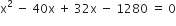
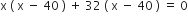
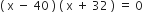
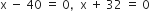
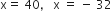
लेकिन रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती
x = 4
इसलिए, रेलगाड़ी की चाल = 40 km/h
गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए:
x2 – 3x – 10 = 0
x2 – 3x – 10 = 0
⇒ x2 – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) =0
⇒ (x – 5) (x + 2) = 0
⇒ x – 5 = 0, x + 2 = 0
x = 5, x = – 2
अत: दिए हुए द्विघात समीकरण के मूल 5 और - 2 हैं।
गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए:
2x2 + x – 6 = 0
2x2 + x – 6 = 0
a = 2, b = 1, c = – 6
ac = – 12 = 4 x (– 3 )
b = 1 = 4 – 3
∴ 2x2 + x – 6 = 0
⇒ 2x2 + 4x – 3x – 6 = 0
⇒ 2x(x + 2) – 3(x + 2) = 0
⇒ (x + 2) (2x – 3) = 0
⇒ x + 2 = 0, 2x - 3 = 0
⇒ x = –2, x = 3/2
अत: दिए हुए द्विघात समीकरण के मूल - 2 और 3/2 हैं
गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए:
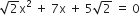
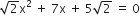
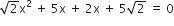
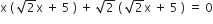
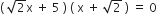
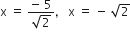
अत: दिए हुए द्विघात समीकरण के मूल
 हैं।
हैं।
गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए:
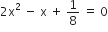
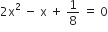
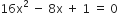
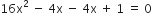
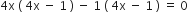
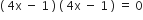
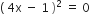
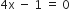
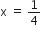 ,
, 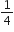
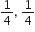 हैं।
हैं।
गुणनखंड विधि से निम्न द्विघात समीकरणों के मूल ज्ञात कीजिए:
100x2 - 20x + 1 = 0
100x2 - 20x + 1 = 0![]() 100x2 - 10x - 10x + 1 = 0
100x2 - 10x - 10x + 1 = 0![]() 10x (10x - 1) - 1(10x - 1) = 0
10x (10x - 1) - 1(10x - 1) = 0![]() (10x - 1) (10x - 1) = 0
(10x - 1) (10x - 1) = 0![]() (10x - 1)2 = 0
(10x - 1)2 = 0![]() 10x - 1 =0
10x - 1 =0![]()
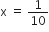 ,
, 
अत: दिए हुए द्विघात समीकरण के मूल  हैं।
हैं।
Sponsor Area
ऐसी दो संख्याएँ ज्ञात कीजिए, जिनका योग 27 हो और गुणनफल 182 हो।
तो दूसरी संख्या = 27 - x
प्रश्नानुसार,
x(27 – x) = 182
⇒ 27x – x2 = 182
⇒ x2 – 27x + 182 = 0
⇒ x2 – 14x – 13x + 182 = 0
⇒ x(x – 14) – 13 (x – 14) = 0
⇒ (x – 13) (x – 14) = 0
x – 13 = 0, x – 14 = 0
⇒ x = 13, x = 14
यदि x = 13
तो दूसरी संख्या = 21 – x
= 27 – 13 = 14
यदि x = 14
तो दूसरी संख्या = 27 - x
= 27 – 14 = 13
अत: संख्याएँ 13 और 14 हैं।
दो क्रमागत धनात्मक पूर्णांक ज्ञात कीजिए जिनके वर्गों का योग 365 हो।
इसलिए दूसरी धनात्मक पूर्णांक संख्या = x + 1
प्रश्नानुसार,
x2 + (x + 1)2 = 365 x2 + x2 + 1 + 2x = 365
⇒ 2x2 + 2x – 364 = 0
⇒ x2 + x – 182 = 0
⇒ x2 + 14x – 13x – 182 = 0
⇒ x(x + 14) – 13(x + 14) = 0
⇒ (x – 13) (x + 14) = 0
⇒ x – 13 = 0, x + 14 = 0
⇒ x = 13, x = – 14
परन्तु दिए हुए पूर्णांक धनात्मक है इसलिए,
अत: अभीष्ट धनात्मक पूर्णांक 13 और 14 हैं।
एक समकोण त्रिभुज की ऊँचाई इसके आधार से 7 cm कम है। यदि कर्ण 13 cm का हो, तो अन्य दो भुजाएँ ज्ञात कीजिए।
माना आधार (BC) = x cm
तो ऊँचाई (AB) = (x – 7) cm
कर्ण (AC) = 13 cm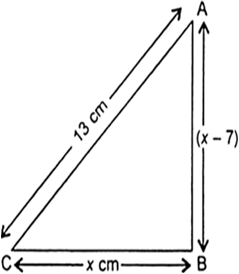
पाइथागोरस प्रमेय द्वारा,AC2 = AB2 + BC2
⇒ (13)2 = (x – 7)2 + (x)2
⇒ 169 = x2 + 49 – 14x + x2
⇒ 169 = 2x2 – 14x + 49
⇒ 2x2 – 14x – 120 = 0
⇒ x2 – 7x – 60 = 0
⇒ x2 – 12x + 5x – 60 = 0
⇒ x(x - 12) + 5(x – 12) = 0
⇒ (x + 5) (x – 12) = 0
⇒ x + 5 = 0, x - 12 = 0
⇒ x = –5, x = 12
भुजा कभी भी ऋणात्मक नहीं होती, इसलिए
x = 12
ऊँचाई (AB) = x – 7
= 12 – 7 = 5 cm
आधार (BC) = x = 12 cm
एक कुटीर उद्योग एक दिन में कुछ बर्तनों का निर्माण करता है। एक विशेष दिन यह देखा गया कि प्रत्येक नग की निर्माण लागत ( रुपयों ) उस दिन के निर्माण किए बर्तनों की संख्या के दुगुने से 3 अधिक थी। यदि उस दिन की कुल निर्माण लागत 90 रु. थी, तो निर्मित बर्तनों की संख्या और प्रत्येक नग की लागत ज्ञात कीजिए।
माना बनाए गए बर्तनों की संख्या = x
बनाए गए बर्तनों की संख्या = (2x + 3) रु.
So, total cost of production that day = Rs. x(2x + 3)
प्रश्नानुसार,
x(2x + 3) = 90
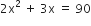
![]()
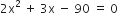
![]()
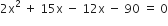
![]()

![]()
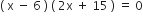
![]()
 ,
, 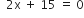

 ,
, 
![]()
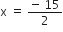
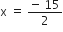 नहीं हो सकता
नहीं हो सकता
इसलिए, x = 6
बनाए गए बर्तनों की संख्या = 6
प्रत्येक बर्तन का मूल्य = (2 x 6 + 3) = 15 रु.
यदि निम्नलिखित द्विघात समीकरणों के मूलों का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए।
2x2 – 7x + 3 = 0

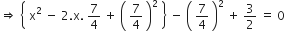
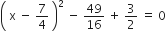
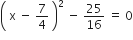
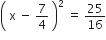
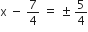
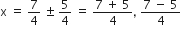
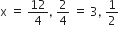
द्विघात समीकरण के मूल हैं: 3,
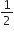
यदि निम्नलिखित द्विघात समीकरणों के मूलों का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए।
2x2 + x - 4 = 0
2x2 + x - 4 = 0![]()
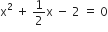
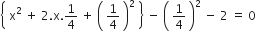
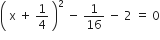
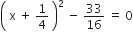
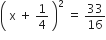
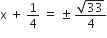
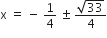
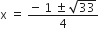
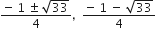
यदि निम्नलिखित द्विघात समीकरणों के मूलों का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए।
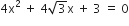
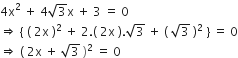

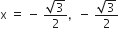
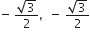
यदि निम्नलिखित द्विघात समीकरणों के मूलों का अस्तित्व हो तो इन्हें पूर्ण वर्ग बनाने की विधि द्वारा ज्ञात कीजिए।
2x2 + x + 4 = 0
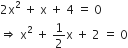
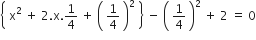
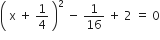

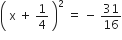
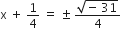
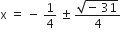
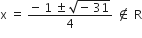
निम्न समीकरणों के मूल ज्ञात कीजिए:
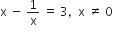
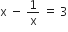
![]()
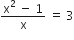
![]()
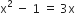
![]()
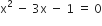

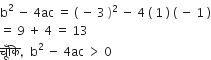
द्विघात सूत्र द्वारा,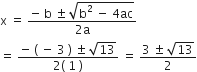
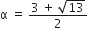
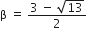
अत: दिए गए द्विघात समीकरण के मूल हैं: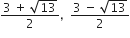
3 वर्ष पूर्व रहमान की आयु ( वर्षों में ) का व्युत्क्रम और अब से 5 वर्ष पश्चात आयु के व्युत्क्रम का योग 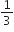 है। उसकी वर्तमान आयु ज्ञात कीजिए।
है। उसकी वर्तमान आयु ज्ञात कीजिए।
3 वर्ष पहले उसकी आयु = (x – 3) वर्ष
5 वर्ष बाद उसकी आयु = (x + 5) वर्ष
प्रश्नानुसार,
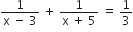
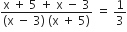
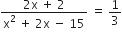
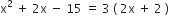
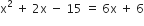
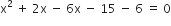
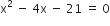
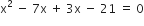
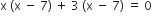
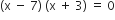
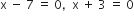
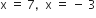
आयु ऋणात्मक नहीं हो सकती,
इसलिए x = 7
तो रहमान की वर्तमान आयु = 7 वर्ष
एक क्लास टेस्ट में शेफाली के गणित और अंग्रेजी में प्राप्त अंकों का योग 30 है। यदि इसको गणित में 2 अंक अधिक और अंग्रेजी में 3 अंक कम मिले होते, तो उनके अंकों का गुणनफल 210 होता। उसके द्वारा दोनों विषयों में प्राप्त अंक ज्ञात कीजिए।
माना शेफाली के गणित में प्राप्त अंक = x
तब उसके अंग्रेजी में प्राप्त अंक = (30 – x)
प्रश्नानुसार,
(x + 2) (30 – x – 3) = 210 (x + 2) (27 – x) = 210
⇒ 27x – x2 + 54 – 2x – 210 = 0
⇒ –x2 + 25x – 156 = 0
⇒ x2 – 25x + 156 = 0
x2 – 13x – 12x + 156 = 0
⇒ x(x – 13) – 12(x – 13) = 0
⇒ (x – 13) (x – 12) = 0
⇒ x – 13 = 0, x – 12 = 0
x = 13, x = 12
अत: यदि उसके गणित में प्राप्त अंक = 13, तब उसके अंग्रेजी में प्राप्त अंक = 17
और यदि उसके गणित में प्राप्त अंक =12, तब उसके अंग्रेजी में प्राप्त अंक = 30 – 12 = 18
एक आयताकार खेत का विकर्ण उसकी छोटी भुजा से 60 मी. अधिक लंबा है। यदि बड़ी भुजा छोटी भुजा से 30 मी. अधिक हो, तो खेत की भुजाएँ ज्ञात कीजिए।
तब बड़ी भुजा होगी = (x + 30) मी.
और खेत का विकर्ण = (x + 60) मी.
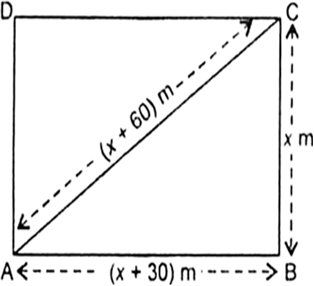
अब समकोण ΔABC में, पाइथागोरस परिमेय द्वारा,
AB2 + BC2 = AC2
⇒ (x + 30)2 + x2 = (x + 60)2
⇒ x2 + 60x + 900 + x2 = x2 + 120x + 3600
⇒ 2x2 + 60x + 900 = x2 + 120x + 3600
⇒ 2x2 – x2 + 60x – 120x + 900 – 3600 = 0
⇒ x2 – 60x – 2700 = 0
यह x में एक द्विघात समीकरण है।
द्विघात सूत्र द्वारा हल करने पर
a = 1, b = - 60, c=- 2700
∴
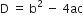
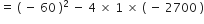

∴
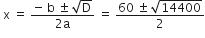
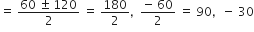
आय की भुजा ऋणात्मक नहीं हो सकती
∴ x = 90
अत: खेत की छोटी भुजा = 90 मी.
खेत की बड़ी भुजा = 90 + 30 = 120 मी.
दो संख्याओं के वर्गों का अंतर 180 है। छोटी संख्या का वर्ग बड़ी संख्या का आठ गुना है। दोनों संख्याएं ज्ञात कीजिए।
माना छोटी संख्या = x
और बड़ी संख्या = y
प्रश्नानुसार,
x2 = 8y ...(i)
y2 - x2 = 180 ...(ii)
समीकरण (i) और (ii) से
y2 - 8y = 180![]() y2 - 8y - 180 = 0
y2 - 8y - 180 = 0
यह y में एक द्विघात समीकरण है।
गुणनखंड विधि द्वारा हल करने पर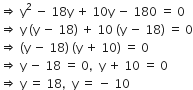
जब y = - 10, तब 
![]()

∴ 
जब y = 18, तब x = 8 x 18 = 144![]()

यदि छोटी संख्या = 12
तब बड़ी संख्या = 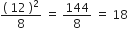
यदि छोटी संख्या = - 12
तब बड़ी संख्या = 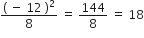
एक रेलगाड़ी एक समान चाल से 360 km की दूरी तय करती है। यदि यह चाल 5 km/h अधिक होती, तो वह उसी यात्रा में 1 घंटा कम समय लेती। रेलगाड़ी की चाल गीत कीजिए।
दूरी = 360 km
∴ 360 km दूरी तय करने में लगा समय =
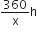
यदि चाल 5 km/h अधिक होती तब
तब, 360 km दूरी तय करने में लगा समय =
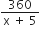 h
hप्रश्नानुसार,
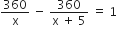
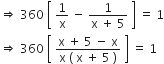
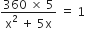
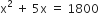
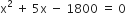
यह x में एक द्विघात समीकरण है।
गुणनखंड विधि द्वारा हल करने पर
⇒ x2 + 45x – 40x – 1800 = 0
⇒ x (x + 45) – 40 (x + 45) = 0
⇒ (x + 45) (x – 40) = 0
⇒ x + 45 = 0, x – 40 = 0
⇒ x = – 45, x = 40
लेकिन चाल कभी ऋणात्मक नहीं हो सकती
∴ x = 40
अत: रेलगाड़ी की चाल = 40 km/h
दो पानी के नल एक साथ एक हौज को 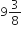 घंटो में भर सकते हैं। बड़े व्यास वाला नल हौज को भरने में, कम व्यास वाले नल से 10 घंटे कम समय लेता है। प्रत्येक द्वारा अलग से हौज को भरने के समय ज्ञात कीजिए।
घंटो में भर सकते हैं। बड़े व्यास वाला नल हौज को भरने में, कम व्यास वाले नल से 10 घंटे कम समय लेता है। प्रत्येक द्वारा अलग से हौज को भरने के समय ज्ञात कीजिए।
∴ छोटे व्यास वाला नल हौज को भरने में समय लेता है = (x + 10) घंटे
1 घंटे में बड़े व्यास वाला नल हौज को भरता है =

1 घंटे में छोटे व्यास वाला नल हौज को भरता है =
1 घंटे में दोनों नल मिलकर हौज को भरते है
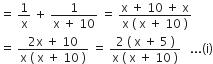
1 घंटे में दोनों नल मिलकर हौज को भरते है =
 ...(ii) [ दिया है ]
...(ii) [ दिया है ]∴ समीकरण (i) और (ii) से
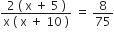
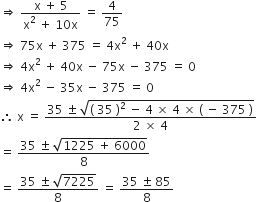
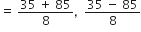
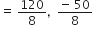
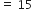 , नल द्वारा लिया गया समय ऋणात्मक नहीं हो सकता
, नल द्वारा लिया गया समय ऋणात्मक नहीं हो सकताअत: बड़े नल द्वारा हौज भरने में लिया गया समय = 15 h
छोटे नल द्वारा हौज भरने में लिया गया समय = (15 +10) = 25 h
मैसूर और बैंगलोर के बीच के 132 km यात्रा करने में एक एक्सप्रेस रेलगाड़ी, सवारी गाडी से 1 घंटा कम समय लेती है। ( मध्य के स्टेशनों पर ठहरने का समय ध्यान में न लिया जाए )। यदि एक्सप्रेस रेलगाड़ी की औसत चाल, सवारी गाड़ी की औसत चाल से 11 km/h अधिक हो, तो दोनों रेलगाड़ियों की औसत चाल ज्ञात कीजिए।
तब एक्सप्रेस रेलगाड़ी की औसत चाल = (x + 11) km/h
दूरी = 132 km
132 km दूरी तय करने में सवारी गाड़ी द्वारा लिया गया समय =
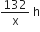
132 km दूरी तय करने में एक्सप्रेस रेलगाड़ी द्वारा लिया गया समय =
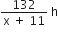
प्रश्नानुसार,
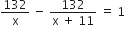

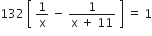
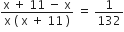
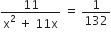
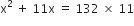
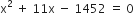
यह x में एक द्विघात समीकरण है।
द्विघात सूत्र द्वारा हल करने पर
a = 1, b = 11, c = - 1452
∴
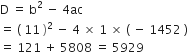
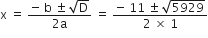
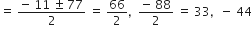
रेलगाड़ी की चाल ऋणात्मक नहीं हो सकती
∴ x = 33
अत: सवारी गाड़ी की औसत चाल = 33 km/h
एक्सप्रेस रेलगाड़ी की औसत चाल = 33 + 11 = 44 km/h
दो वर्गों के क्षेत्रफलों का योग 468 m2 है। यदि उसके परिमापों का अंतर 24 m हो, तो दोनों वर्गों की भुजाएँ ज्ञात कीजिए।
माना पहले वर्ग की भुजा = x m
और दूसरे वर्ग की भुजा = y m
पहले वर्ग का क्षेत्रफल = x2 m2
दूसरे वर्ग का क्षेत्रफल = y2 m2
पहले वर्ग का परिमाप = 4x m
दूसरे वर्ग का परिमाप = 4y m
प्रश्नानुसार,
x2 + y2 = 468 ...(i)
4x – 4y = 24
⇒ x – y = 6 ...(ii)
समीकरण (ii) से
x = 6 + y ...(iii)
x का मान समीकरण (i) में रखने पर
(6 + y)2 + y2 = 468 ⇒ 36+12y + y2 + y2 = 468 ⇒ 2y2 + 12y + 36 – 468 =0
⇒ 2y2 + 12y – 432 = 0
⇒ y2 + 6y – 216 = 0
यह y में द्विघात समीकरण है।
द्विघात सूत्र द्वारा हल करने पर
a = 1, b = 6, c = - 216
∴ 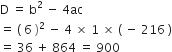
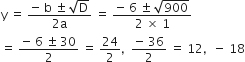
लेकिन वर्ग की भुजा कभी ऋणात्मक नहीं होती
y = 12
y का मान समीकरण (iii) में रखने पर
x = 6 + 12 = 18
अत: पहले वर्ग की भुजा = 18 m
और दूसरे वर्ग की भुजा = 12 m
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का आस्तित्व हो तो उन्हें ज्ञात कीजिए:
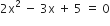
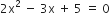
यहाँ, 
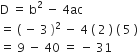
चूँकि, D < 0
अत: दिए गए समीकरण का कोई वास्तविक मूल नहीं है।
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का आस्तित्व हो तो उन्हें ज्ञात कीजिए:
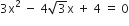
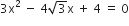
यहाँ, 
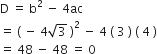
चूँकि, D = 0
अत: दिए गए समीकरण के दो समान मूल हैं।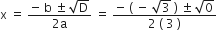
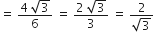
अत: मूल हैं 
निम्न द्विघात समीकरणों के मूलों की प्रकृति ज्ञात कीजिए। यदि मूलों का आस्तित्व हो तो उन्हें ज्ञात कीजिए:
2x2 - 6x + 3 = 0
यहाँ, a = 2, b = – 6, c = 3
D = b2 – 4ac
= ( – 6 )2 – 4 ( 2 ) ( 3 )
= 36 – 24 = 12
चूँकि, D > 0
अत: दिए गए दवहीघाट समीकरण के दो वास्तविक मूल हैं।
द्विघात सूत्र दवरा हल करने पर
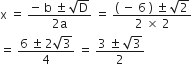
अत: मूल हैं
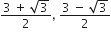
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों।
2x2 + kx + 3 = 0
2x2 + kx + 3 = 0
यहाँ, a = 2, b = k, c = 3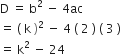
दो समान मूल के लिए,
D = 0![]() b2 - 4ac
b2 - 4ac![]() k2 - 24
k2 - 24![]() k2 = 24
k2 = 24![]()

![]()

![]()
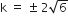
निम्न प्रत्येक द्विघात समीकरण में k का ऐसा मान ज्ञात कीजिए कि उसके दो बराबर मूल हों।
kx (x – 2) + 6 = 0
kx (x – 2) + 6 = 0
⇒ kx2 – 2kx + 6 = 0
यहाँ, a = K, b = – 2k, c = 6
D = b2 – 4ac
⇒ D = ( – 2k )2 – 4(k) (6)
D = 4k2 – 24k
मूल बराबर के लिए, D = 0
⇒ 4k2 – 24k = 0
⇒ 4 k (k – 6) = 0
⇒ 4k = 0, k – 6 = 0
⇒ K = 0, k = 6
Sponsor Area
क्या एक ऐसी आम की बगिया बनाना संभव है। जिसकी लंबाई, चौड़ाई से दुगुनी हो और उसका क्षेत्रफल 800 m2 हो? यदि है, तो उसकी लंबाई और चौड़ाई ज्ञात कीजिए।
तो लंबाई = 2 m
प्रश्नानुसार,
क्षेत्रफल = 800
⇒ 2 x ( x ) = 800
⇒ 2x2 = 800
⇒ x2 = 400
⇒ x2 – 400 = 0
⇒ x2 = 400
⇒
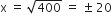
⇒ x = 20 [ चौड़ाई को ऋणात्मक नहीं ले सकते ]
अत: चौड़ाई = 20 m
और लंबाई = 2 x 20 = 40 m
क्या निम्न स्थिति संभव है? यदि है, तो उनकी वर्तमान आयु ज्ञात कीजिए।
दो मित्रों की आयु का योग 20 वर्ष है। चार वर्ष पूर्व उनकी आयु ( वर्षों में ) का गुणनफल 48 था।
माना पहले मित्र की वर्तमान आयु = x वर्ष
तब, दूसरे मित्र की वर्तमान आयु = (20 -x) वर्ष
4 वर्ष पूर्व,
पहले मित्र की आयु = (x - 4) वर्ष
दूसरे मित्र की आयु = 20 - x - 4 = (16 - x) वर्ष
प्रश्नानुसार,
(x – 4) (16 – x) = 48
⇒ 16 x – x2 – 64 + 4x = 48
⇒ – x2 + 20x – 112 = 0
⇒ x2 – 20x + 112 = 0
यहाँ, a = 1, b = – 20, c = 112
D = b2 – 4 ac
= ( – 20 )2 – 4 ( 1 ) ( 112 ) = 400 – 448 = – 48
चूँकि, D < 0
इसलिए, द्विघात समीकरण का कोई वास्तविक मान नहीं है।
अत: उपरोक्त स्थिति संभव नहीं है।
क्या परिमाप 80 m तथा क्षेत्रफल 400 m2 के एक पार्क को बनाना संभव है? यदि है, तो उसकी लंबाई और चौड़ाई ज्ञात कीजिए।
माना आयताकार पार्क की लंबाई = x m
और आयताकार पार्क की चौड़ाई = y m
प्रश्नानुसार,
परिमाप = 2(x + y) m
⇒ 2 (x + y) = 80
⇒ x + y = 40
⇒ y = 40 – x
चौड़ाई = (40 – x)m
क्षेत्रफल = 400
⇒ x x y = 400
⇒ x(40 – x) = 400
40x – x2 = 400
⇒ x2 – 40x + 400 = 0
यहाँ, a = 1, b = – 40, c = 400
D = b2 – 4ac
= ( – 40 )2 – 4 ( 1 ) ( 400 ) = 1600 – 1600 = 0
चूँकि, D = 0इसलिए, द्विघात समीकरण के दोनों मूल समान हैं।
द्विघात सूत्र द्वारा हल करने पर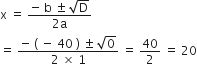
अत: आयताकार पार्क की लंबाई = 20 m
और चौड़ाई = 40 - 20 = 20 m
अत: एक वर्गाकार पार्क को बनाना संभव है जिसकी प्रत्येक भुजा 20 m होगी।
एक वायुयान अपने निर्धारित समय से 30 मिनट के विलम्ब से चला । 1500 किलोमीटर की दूरी पर अपने गंतव्य पर ठीक समय पर पहुँचने के लिए इसे अपनी सामान्य चाल को 100 कि.मी./घंटा बढ़ाना पड़ा। वायुयान की सामान्य चाल ज्ञात कीजिए ।
विमान की सामान्य गति = x km/hr
विमान की गति में वृद्धि = (x + 100)km/hr
माना सामान्य गति से गंतव्य तक पहुँचने के लिए समय लगता है,
वृद्धि गति से गंतव्य तक पहुँचने के लिए समय लगता है,
दोनों समय का अंतर = t1 - t2 =30 min = 1/2
लेकिन गति नकारात्मक नहीं हो सकती है इसलिए, सामान्य गति 500 किमी / घंटा।
एक मोटरबोट जिसकी स्थिर जल में चाल 18 किमी घंटा है, 24 किलोमीटर धारा के प्रतिकूल जाने में, वही दूरी धारा के अनुकूल जाने की अपेक्षा 1 घंटा अधिक लेती है । धारा की चाल ज्ञात कीजिए।
माना धारा की गति x km/hr
अब, नदी के ऊपर के लिए, गति = (18-x) km/hr
अब, नदी के नीचे की ओर गति
यह दिया हुआ की,
एक रेलगाड़ी किसी औसत चाल से 63 किमी की दूरी तय करती है तथा उसके बाद 72 किमी की दूरी मूल औसत चाल से 6 किमी/घंटा अधिक की चाल से तय करती है । पूरी यात्रा को पूरा करने में यदि 3 घंटे लगते हैं, तो मूल औसत चाल ज्ञात कीजिए।
मूल औसत गति x
यात्रा को पूरा करने के लिए 3 घंटे लगे
गति कभी नकारात्मक नहीं हो सकती है।
इसलिए x = 42 किमी / घंटा।
एक समांतर श्रेढ़ी के चार क्रमागत पदों की संख्याओं का योग 32 है तथा पहली और आखिरी संख्या के गुणनफल का बीच की दो संख्याओं के गुणनफल से अनुपात 7 : 15 है, संख्याएँ ज्ञात कीजिए ।
4 नंबर जो AP क्रम में है
(a -3d),(a-d), (a+d) and (a+3d)
∴ (a-3d) + (a-d) +(a+ d) + (a +3d) = 32
⇒ 4a = 32
a =8
Mock Test Series
Sponsor Area
Sponsor Area






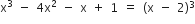
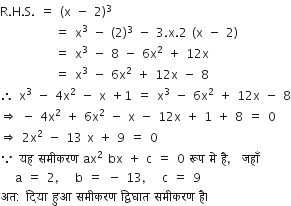
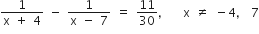
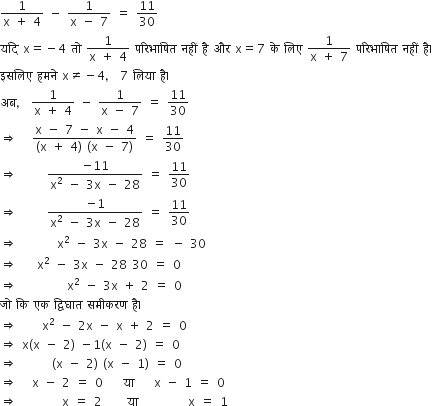
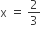 तथा x = -3 एक द्विघाती समीकरण
तथा x = -3 एक द्विघाती समीकरण 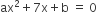 के मूल हैं, तो a तथा b के मान ज्ञात कीजिए।
के मूल हैं, तो a तथा b के मान ज्ञात कीजिए। 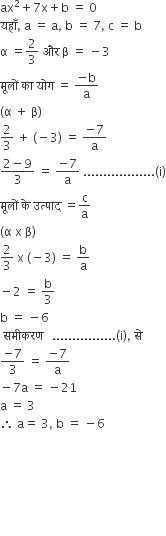
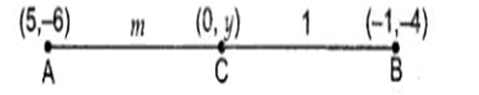
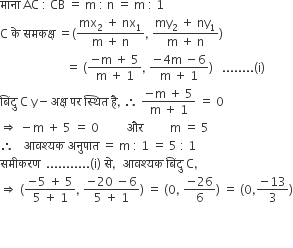
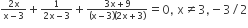
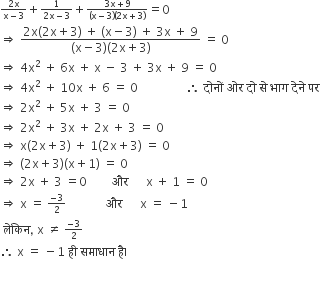
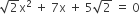 के मूल ज्ञात कीजिए।
के मूल ज्ञात कीजिए। 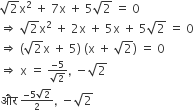
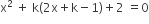 के मूल वास्तविक तथा समान हैं।
के मूल वास्तविक तथा समान हैं।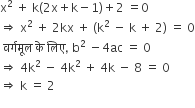
 के मूल समान हों तो दर्शाइए कि
के मूल समान हों तो दर्शाइए कि 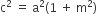 ।
।