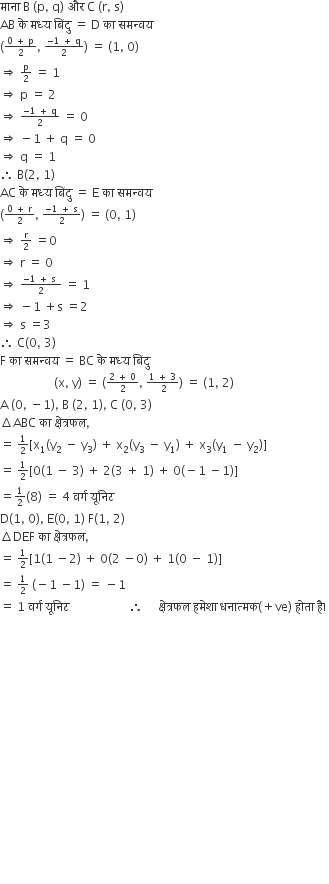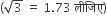गणित Chapter 12 वृतों से संबंधित क्षेत्रफल
Sponsor Area
NCERT Solution For Class 10 गणित गणित
दो वृतों की त्रिज्याएँ क्रमश: 19 cm और 9cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसकी परिधि इन दोनों वृतों की परिधियों के योग के बराबर है।
यहाँ पर, पहले वृत्त की त्रिज्या 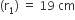
दूसरे वृत्त की त्रिज्या (r2) = 9 cm
माना वांछित वृत्त की त्रिज्या = R cm
प्रश्नानुसार, वांछित वृत्त की परिधि = पहले वृत्त की परिधि + दूसरे वृत्त की परिधि 

 R =
R =  (दोनों ओर
(दोनों ओर  से भाग करने पर)
से भाग करने पर)
= (19 + 9)cm = 28 cm
अत: वांछित वृत्त की त्रिज्या = 28 cm
दो वृतों की त्रिज्याएँ क्रमश: 8cm और 6cm हैं। उस वृत्त की त्रिज्या ज्ञात कीजिए जिसका क्षेत्रफल इन दोनों वृतों के क्षेत्रफलों के योग के बराबर है।
यहाँ पर, पहले वृत्त की त्रिज्या (r1) = 8 cm
दूसरे वृत्त की त्रिज्या (r2) = 6 cm
माना वांछित वृत्त की त्रिज्या = R cm
प्रश्नानुसार,
वांछित वृत्त का क्षेत्रफल = पहले वृत्त का क्षेत्रफल + दूसरे वृत्त का क्षेत्रफल 


 (दोनों ओर
(दोनों ओर  से भाग करने पर)
से भाग करने पर)

 = 64 + 36 = 100
= 64 + 36 = 100

 R = 10
R = 10
अत: वांछित वृत्त की त्रिज्या = 10 cm
किसी कार के प्रत्येक पहिए का व्यास 80cm है। यही यह कार 66 प्रति घंटे की चाल से चल रही है, तो 10 मिनट में प्रत्येक पहिया कितने चक्कर लगाता है?
कार के पहिए का व्यास = 80 cm
कार के पहिए की त्रिज्या (r) = 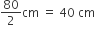
अत: कार के पहिए की परिधि = 
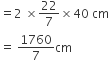
कार की चाल = 66 km/h
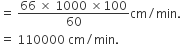
10 मिनट में कार द्वारा तय दूरी = चाल x समय
= 110000 x 10 cm
= 1100000 cm
∴ 10 मिनट में कार के प्रत्येक पहिए द्वारा लगाए गए चक्कराें की संख्या = 
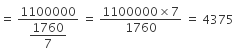
निम्नलिखित में सही उत्तर चुनिए तथा अपने उत्तर का औचित्य दीजिए:
यदि एक वृत्त का परिमाप और क्षेत्रफल संख्यात्मक रूप में बराबर है, तो उसे वृत्त की त्रिज्या है:
-
2 मात्रक
-
 मात्रक
मात्रक
-
4 मात्रक
-
7 मात्रक
A.
2 मात्रक
वृत्त की त्रिज्या = r मात्रक
तो वृत्त का परिमाप =  मात्रक
मात्रक
वृत्त का क्षेत्रफल =  वर्ग मात्रक
वर्ग मात्रक
प्रश्नानुसार, 
 r = 2
r = 2
अत: वृत्त की त्रिज्या = 2 मात्रक
6cm त्रिज्या वाले एक वृत्त के एक त्रिज्यखंड का क्षेत्रफल ज्ञात कीजिए, जिसका कोण  है।
है।
यहाँ पर, वृत्त की त्रिज्या (r) = 6 cm
त्रिज्यखंड का कोण 
∴ त्रिज्यखंड का क्षेत्रफल = 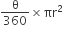
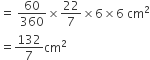
एक वृत्त, के चतुर्थांश(quadrant) का क्षेत्रफल ज्ञात कीजिए, जिसकी परिधि 22 cm है।
वृत्त की परिधि = 22 cm

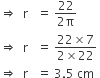
अत: वृत्त के चतुर्थांश का क्षेत्रफल
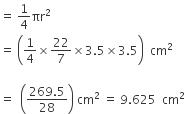
एक घड़ी की मिनट की सुई जिसकी लंबाई 14cm है। इस सुई द्वारा 5 मिनट में रचित क्षेत्रफल ज्ञात कीजिए।
यहाँ पर घड़ी की मिनट की सुई की लंबाई (r) = 14 cm
5 मिनट में मिनट की सुई द्वारा तय कोण 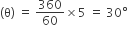
अत: मिनट की सुई द्वारा 5 मिनट में रचित क्षेत्रफल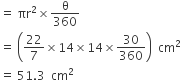
10cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर एक समकोण अंतरित करती है। निम्नलिखित के क्षेत्रफल ज्ञात कीजिए:
(i) संगत लघु वृत्तखंड (ii) संगत दीर्घ त्रिज्यखंड
यहाँ पर वृत्त की त्रिज्या (r) = 10 cm
माना जीवा AB द्वारा वृत्त के केंद्र पर
अंतरित कोण 
 लघु वृत्तखंड द्वारा केंद्र पर अंतरित कोण
लघु वृत्तखंड द्वारा केंद्र पर अंतरित कोण 
तथा दीर्घ वृत्तखंड द्वारा केंद्र पर अंतरित कोण 


(i) संगत लघु वृत्तखंड का क्षेत्रफल = त्रिज्यखंड OAPB का क्षेत्रफल - त्रिभुज AOB का क्षेत्रफल
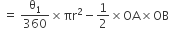
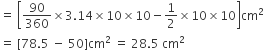
(ii) संगत दीर्घखंड OAQB का क्षेत्रफल = 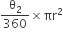
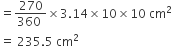
त्रिज्या 21cm वाले वृत्त का एक चाप केंद्र पर 60° का कोण अंतरित करता है। ज्ञात कीजिए-
(i) चाप की लंबाई
(ii) चाप द्वारा बनाए गए त्रिज्यखंड का क्षेत्रफल
(iii) संगत जीवा द्वारा बनाए गए वृत्तखंड का क्षेत्रफल
यहाँ पर, वृत्त की त्रिज्या (r) = 21 cm
चाप APB द्वारा केंद्र पर
अंतरित कोण 
(i) चाप APB की लंबाई = 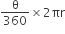
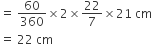
(ii) त्रिज्यखंड OAPB का क्षेत्रफल = 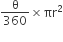
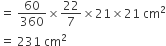

(iii) त्रिभुज OAB का क्षेत्रफल = 
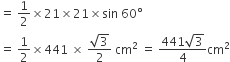
संगत जीवा AB द्वारा बनाए गए छायांकित वृत्तखंड का क्षेत्रफल = (त्रिज्यखंड OAPB - त्रिभुज OAB) का क्षेत्रफल
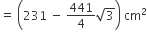
15cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
r = 15 cm,  = 60°
= 60°
माना जीवा द्वारा केंद्र पर अंतरित कोण 
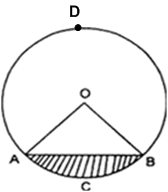
(i) लघु त्रिज्याखंड OACBO का क्षेत्रफल 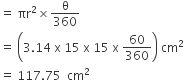
(ii) त्रिभुज OAB का क्षेत्रफल 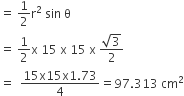
(iii) वृत्त का क्षेत्रफल = 
= 3.14 x 15 x 15 cm2
= 706.5 cm2
अब,
लघु वृत्तखंड ACB का क्षेत्रफल = (त्रिज्यखंड OACBO - त्रिभुज OAB) का क्षेत्रफल
= (117.75 - 97.313) cm2
= 20.4375 cm2
दीर्घ वृत्तखंड (ABDA) का क्षेत्रफल = वृत्त का क्षेत्रफल - लघुखंड का क्षेत्रफल
= (706.5 - 20.4375) cm2
= 686.0625 cm2
त्रिज्या 12 cm वाले एक वृत्त की कोई जीवा केंद्र पर 120° का कोण अंतरित करती है। संगत वृत्तखंड का क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, वृत की त्रिज्या (r) = 12 cm
जीवा AB द्वारा केंद्र पर अंतरित कोण 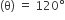
त्रिज्यखंड OAPB का क्षेत्रफल = 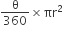
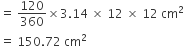

त्रिभुज OAB का क्षेत्रफल 
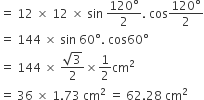
संगत लघु वृत्तखंड APB(छायांकित) का क्षेत्रफल = (त्रिज्यखंड OAPB - त्रिभुज OAB) का क्षेत्रफल
= (150.72 - 62.28) cm2
= 88.44 cm2
15m भुजा वाले एक वर्गाकार घास के मैदान के एक कोने पर लगे खूँटे से एक घोड़े की लंबी रस्सी से बाँध दिया गया है (देखिये सलंग्न आकृति)। ज्ञात कीजिए-
(i) मैदान के उस भाग का क्षेत्रफल जहाँ घोड़ा घास चर सकता है।
(ii) चरे जा सकने वाले क्षेत्रफल में वृद्धि, यदि घोड़े को लंबी रस्सी के स्थान पर लंबी रस्सी से बाँध दिया जाए। ( का प्रयोग कीजिए।)
का प्रयोग कीजिए।)

(i) पहली अवस्था में, मैदान के उस भाग का क्षेत्रफल जहाँ तक घोड़ा चर सकता है
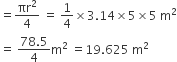
(ii) दूसरी अवस्था में,
मैदान के उस भाग का क्षेत्रफल जहाँ तक घोड़ा चर सकता है
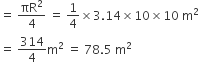
अत: दूसरी अवस्था में चर जा सकने वाले क्षेत्रफल में वृद्धि = (78.5 - 19.625)m2
= 58.875 m2
एक वृत्ताकार ब्रूच (brooch) को चाँदी के तोर से बनाया जाना है जिसका व्यास 35 mm है। तार को वृत्त के 5 व्यासों को बनाने में भी प्रयुक्त किया गया है जो उसे 10 बराबर त्रिजयखंडों में विभाजित करता है जैसा कि सलंग्न आकृति में दर्शाया गया है। तो ज्ञात कीजिए- 
(i) कुल वांछित चाँदी के तार की लम्बाई
(ii) ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल
(i) यहाँ पर,
वृत्ताकार ब्रूच का व्यास (d) = 35 mm
वृत्ताकार ब्रूच की त्रिज्या (r) = 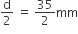
∴ वृत्ताकार ब्रूच की परिधि के लिए आवश्यक चाँदी की तार की लम्बाई = 
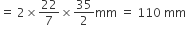
10 बराबर त्रिज्यखंडों में बाँटने एक लिए 5 व्यासों के लम्बाई के लिए आवश्यक चाँदी की तार = 35 x 5mm = 175 mm
अत: कुल आवश्यक चाँदी की तार की लम्बाई = (110 + 175)mm = 285 mm
(ii) यहाँ पर, वृत्ताकार ब्रूच के प्रत्येक त्रिज्यखंड द्वारा केंद्र पर अंतरित कोण 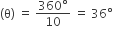
त्ताकार ब्रूच के प्रत्येक त्रिज्यखंड की त्रिज्या (r) = 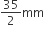
अत: वृत्ताकार ब्रूच के प्रत्येक त्रिज्यखंड का क्षेत्रफल = 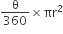
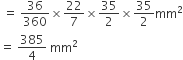
एक छतरी में आठ ताने हैं, जो बराबर दूरी पर लागए हुए हैं (देखिए आकृति)। छतरी को 45 cm त्रिज्या वाला एक सपाट वृत्त मानते हुए , इसकी दो क्रमागत तानों के बीच का क्षेत्रफल ज्ञात कीजिए।
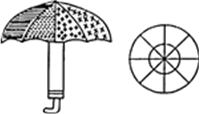
यहाँ पर,
छतरी के दो क्रमागत तानों के बीच त्रिजयखंड द्वारा केंद्र पर
अंतरित कोण 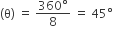
छतरी के वृत्ताकार भाग की त्रिज्या (r) = 45 cm
अत: छतरी के दो क्रमागत तानों के बीच का क्षेत्रफल: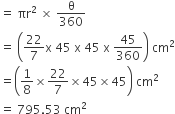
किसी कार के दो वाइपर (Wipers) हैं, परस्पर कभी आच्छादित नहीं होते हैं। प्रत्येक वाइपर की पत्ती की लंबाई 25cm है और  के कोण तक घूम कर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
के कोण तक घूम कर सफाई कर सकता है। पत्तियों की प्रत्येक बुहार के साथ जितना क्षेत्रफल साफ हो जाता है, वह ज्ञात कीजिए।
यहाँ पर, कार का प्रत्येक वाइपर जितने त्रिज्यखंड वाले वृत्त के क्षेत्र को साफ कर सकता है। इसके लिए,
त्रिज्या (r) = 25cm
त्रिज्यखंड कोण 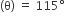
क्षेत्रफल (A) = 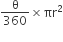
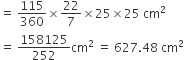
जहाज़ों को समुद्र में जलस्तर के नीचे स्थित चट्टानों की चेतावनी देने के लिए, एक लाइट हाउस(light house) 80° कोण वाले एक त्रिज्यखंड में 16.5 km की दूरी तक लाल रंग का प्रकाश फैलता है। समुद्र के उस भाग का क्षेत्रफल ज्ञात कीजिए जिसमें जहाज़ों को चेतावनी दी जा सके। ( का प्रयोग कीजिए।)
का प्रयोग कीजिए।)
यहाँ पर,
लाइट हाउस द्वारा चेतावनी देने वाले त्रिज्यखंड की त्रिज्या (r) = 16.5 km
लाइट हाउस द्वारा चेतावनी देने वाले त्रिज्यखंड का कोण  = 80°
= 80°
लाइट हाउस द्वारा चेतावनी देने वाले त्रिज्यखंड का क्षेत्रफल (A) = 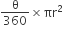
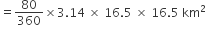
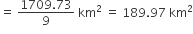
एक गोल मेज़पोश पर छ: समान डिज़ाइन बने हुए हैं जैसाकि आकृति में दर्शाया गया है। यदि मेज़पोश की त्रिज्या 28 cm है, तो 0.35रु प्रति वर्ग सेंटीमीटर की दर से इन डिज़ाईनों को बनाने की लागत ज्ञात कीजिए।

मेज़पोश के प्रत्येक डिज़ाइन की जीवा द्वारा केंद्र पर अंतरित कोण 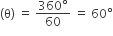
मेज़पोश की त्रिज्या (r) = 28 cm
अत: मेज़पोश के प्रत्येक डिज़ाइन का क्षेत्रफल (A) = 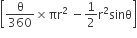
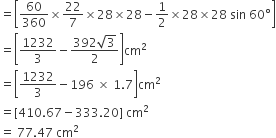
अत: मेज़पोश के डिज़ाइन का कुल क्षेत्रफल = 6 x प्रत्येक त्रिज्यखंड का क्षेत्रफल
= 6 x 77.47 cm2
= 464.82 cm2
1 cm2 डिज़ाइन को बनाने की लागत = 0.35 रु
464.82 cm2 डिज़ाइन को बनाने की लागत = 464.82 x 0.35 रु
= 162.68 रु
Sponsor Area
निम्नलिखित में से सही उत्तर चुनिए-
त्रिज्या वाले वृत्त के उस त्रिज्यखंड का क्षेत्रफल जिसका कोण  है, निम्नलिखित है
है, निम्नलिखित है
D.
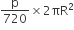
यहाँ पर, वृत्त के त्रिज्यखंड की त्रिज्या (र) = R
वृत्त के त्रिज्यखंड ( ) = P
) = P
∴ वृत्त के त्रिज्यखंड का क्षेत्रफल (A) = 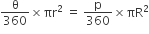
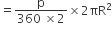 [दोनों ओर 2 से गुणा करने पर]
[दोनों ओर 2 से गुणा करने पर]
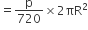
अत:अभीष्ट सही उत्तर = D
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि PQ = 24 cm, PR = 7cm तथा O वृत्त का केंद्र है।
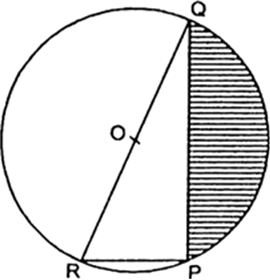
यहाँ पर, PQ = 24 cm
PR = 7 cm
हम जानते हैं कि अर्धवृत में बना कोण 
समकोण त्रिभुज RPQ में पाइथागोरस प्रमेय से,
RQ = 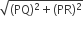
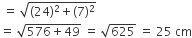
अत: दिए गए वृत्त का व्यास (RQ) = 25 cm
दिए गए वृत्त की त्रिज्या (r) = 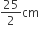
दिए गए वृत्त के छायांकित भाग का क्षेत्रफल = अर्धवृत का क्षेत्रफल - 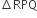 का क्षेत्रफल
का क्षेत्रफल
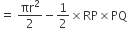
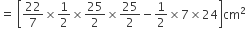
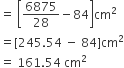
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि केंद्र O वाले दोनों सकेंद्रीय वृतों की त्रिज्याएँ क्रमश: 7cm और 14 cm हैं तथा  है।
है।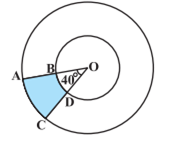
यहाँ पर, बड़े वृत्त की त्रिज्या (R) = 14 cm
छोटे वृत्त की त्रिज्या (r) = 7 cm
चाप तथा चाप द्वारा केंद्र पर अंतरित कोण 
छायांकित त्रिज्यखंड का क्षेत्रफल = (त्रिज्यखंड AOC - त्रिज्यखंड BOD) का क्षेत्रफल
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, यदि ABCD भुजा 14 cm का एक वर्ग है तथा APD और BPC दो अर्धवृत हैं।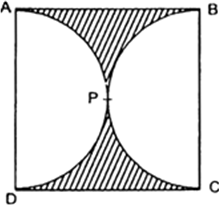
यहाँ पर, वर्ग ABCD की भुजा = 14 cm
वर्ग ABCD का क्षेत्रफल = भुजा x भुजा = (भुजा)2
= 14 x 14 cm2 = 196 cm2
प्रत्येक अर्धवृत की त्रिज्या (r) = 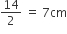
दोनों अर्धवृतों (APD + BPC) का क्षेत्रफल = 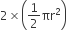
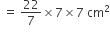
= 154 cm2
अत: आकृति के छायांकित भाग का क्षेत्रफल = (196 - 154) cm2
= 42 cm2
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मान कर 6 cm त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।
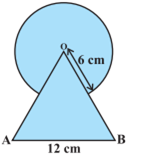
यहाँ पर,  समबाहु त्रिभुज है।
समबाहु त्रिभुज है।

[∵ समबाहु त्रिभुज का प्रत्येक कोण होता है।]
समबाहु  का क्षेत्रफल =
का क्षेत्रफल = 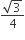 x (भुजा)2
x (भुजा)2
= 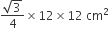
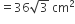
वृत्त की त्रिज्या (r) = 6cm
वृत्त का क्षेत्रफल 
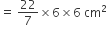
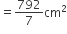
सांझे(common) त्रिज्यखंड का क्षेत्रफल = 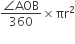
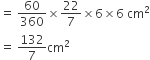
अत: आकृति में छायांकित भाग का कुल क्षेत्रफल 
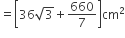
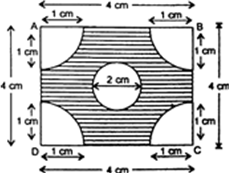
भुजा 4cm वाले एक वर्ग के प्रत्येक कोने से 1 cm त्रिज्या वाले वृत्त का एक चतुर्थांश काटा गया है तथा बीच में 2 cm व्यास का एक वृत्त भी काटा गया है, जैसाकि सलंग्न आकृति में दर्शया गया है। वर्ग के शेष भाग का क्षेत्रफल ज्ञात कीजिए।
यहाँ पर, दिए गए वर्ग की भुजा = 4 cm
दिए गए वर्ग का क्षेत्रफल = भुजा x भुजा
= 4 x 4 cm2 = 16 cm2
कोने से काटे गए वृत्त के प्रत्येक चतुर्थांश की त्रिज्या (r1) = 1 cm
कोने से काटे गए वृत्त के चारों चतुर्थांश का क्षेत्रफल = 4 x प्रत्येक चतुर्थांश का क्षेत्रफल
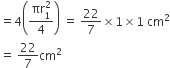
बीच के वृत्त का व्यास = 2 cm
बीच के वृत्त की त्रिज्या 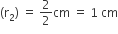
∴ बीच के वृत्त का क्षेत्रफल = 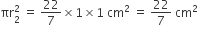
अत: दी गई आकृति के छायांकित भाग का क्षेत्रफल = 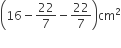
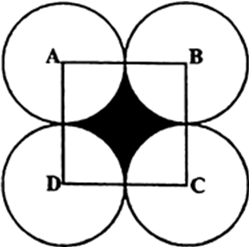
आकृति में, ABCD भुजा 14 cm वाला एक वर्ग है। A, B, C और D को केंद्र मानकर, चार वृत्त इस प्रकार खींचे गए हैं कि प्रत्येक वृत्त तीन शेष वृत्तों में से दो वृत्तों को बाह्य रूप से स्पर्श करता है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
दिए गए वर्ग ABCD की भुजा = 14 cm
∴ दिए गए वर्ग ABCD का क्षेत्रफल = भुजा x भुजा
= (14 x 14)cm2 = 196 cm2
प्रत्येक वृत्त के चतुर्थांश की त्रिज्या (r) = 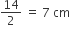
प्रत्येक वृत्त के चतुर्थांश का क्षेत्रफल = 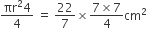
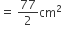
प्रत्येक वृत्त के चारों चतुर्थांशों का क्षेत्रफल = 4 x प्रत्येक चतुर्थांश का क्षेत्रफल
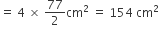
अत: आकृति के छायांकित भाग का क्षेत्रफल = वर्ग का क्षेत्रफल - चार चतुर्थांशों का क्षेत्रफल
= (196 - 154) cm2
= 42 cm2
आकृति एक दौड़ने का पथ (racing track) दर्शाती है, जिसके बाएँ और दाएँ सिरे अर्धवृत्ताकार हैं। 
दोनों आंतरिक समांतर रेखाखण्डों के बीच की दूरी 60m है तथा इनमें से प्रत्येक रेखाखण्ड 106 लंबा है। यदि यह पथ 10m चौड़ा है, तो ज्ञात कीजिए।
(i) पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में चली गई दूरी,
(ii) पथ का क्षेत्रफल।
(i) प्रत्येक आंतरिक अर्धवृत का व्यास = 60 m
प्रत्येक आंतरिक अर्धवृत की त्रिज्या (r) = 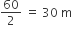
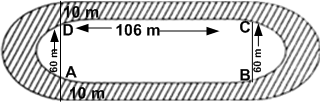
दोनों आंतरिक अर्धवृतों की परिधि = 2 x प्रत्येक अर्धवृत की परिधि
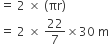
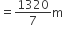
आंतरिक दोनों किनारो की दूरी = AB + CD = (106 + 106)m
= 212 m
अत: पथ के आंतरिक किनारों के अनुदिश एक पूरा चक्कर लगाने में तय दूरी
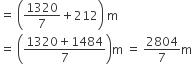
(ii) आंतरिक आयत का क्षेत्रफल = 106 x 60 m2 = 6360 m2
बाहरी आयत का क्षेत्रफल = 106 x 80m2 = 8480 m2
आयातकार छायांकित आकृति का क्षेत्रफल = बाहरी क्षेत्रफल - आंतरिक क्षेत्रफल
= (8480 - 6360)m2 = 2120m2
प्रत्येक बाहरी अर्धवृत्त की त्रिज्या (R) = 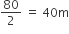
प्रत्येक अर्धवृत्ताकार छायांकित आकृति का क्षेत्रफल = 
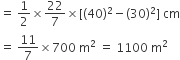
दोनों अर्धवृत्ताकार छायांकित आकृतियों का क्षेत्रफल = 2 x 1100 m2
= 2200 m2
अत: छायांकित कुल पथ का क्षेत्रफल = (2120 + 2200) m2
= 4320 m2
आकृति में, AB और CD केंद्र O वाले एक वृत्त के दो परस्पर लम्ब व्यास हैं तथा छोटे वृत्त का व्यास है। यदि OA = 7 cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।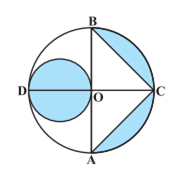
यहाँ पर,
बड़े वृत्त की त्रिज्या (OA) = 7 cm
बड़े वृत्त की त्रिज्या (AB) = 2 x OA = 2 x 7cm = 14 cm
परन्तु OC = OA = 7 cm
 का क्षेत्रफल =
का क्षेत्रफल = 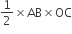
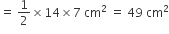
बड़े अर्धवृत्त का क्षेत्रफल = 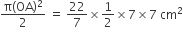
= 77 cm2
दिए गए छोटे वृत्त का व्यास (OD) = 7 cm (बड़े वृत्त की त्रिज्या)
दिए गए छोटे वृत्त की त्रिज्या (r) = 
दिए गए छोटे वृत्त का क्षेत्रफल 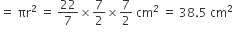
अत: छायांकित भाग का क्षेत्रफल = छोटे वृत्त का क्षेत्रफल + (बड़े अर्धवृत्त का क्षेत्रफल -  का क्षेत्रफल)
का क्षेत्रफल)
= [38.5 + (77 - 49)] cm2
= [38.5 + 28] cm2
= 66.5 cm2
एक समबाहु त्रिभुज ABC का क्षेत्रफल 17320.5 cm2 है। इस त्रिभुज के प्रत्येक शीर्ष को केंद्र मानकर त्रिभुज की भुजा के आधे के बराबर की त्रिज्या लेकर एक वृत्त खींचा जाता है। (देखिए आकृति)। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
समबाहु त्रिभुज ABC का क्षेत्रफल = 17320.5 cm2
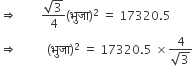
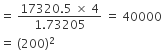
 भुजा = 200 cm
भुजा = 200 cm
अत: प्रत्येक वृत्त की त्रिज्या (r) = 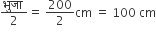
प्रत्येक त्रिज्यखंड का कोण  (समबाहु त्रिभुज का प्रत्येक कोण)
(समबाहु त्रिभुज का प्रत्येक कोण)
 तीनों त्रिज्यखंडों का क्षेत्रफल = 3
तीनों त्रिज्यखंडों का क्षेत्रफल = 3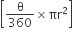
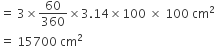
इसी प्रकार, आकृति के छायांकित भाग का क्षेत्रफल =
 का क्षेत्रफल - तीनों त्रिज्यखंडों का क्षेत्रफल
का क्षेत्रफल - तीनों त्रिज्यखंडों का क्षेत्रफल= (17320.5 - 15700)cm2
=1620.5 cm2
एक वर्गाकार रुमाल पर, नौ वृत्ताकार डिज़ाइन बने हैं, जिनमें से प्रत्येक की त्रिज्या 7cm है। रुमाल के शेष भाग का क्षेत्रफल ज्ञात कीजिए। 
यहाँ पर,
रुमाल के प्रत्येक वृत्ताकार डिज़ाइन की त्रिज्या (r) = 7 cm
रुमाल के प्रत्येक वृत्ताकार डिज़ाइन का व्यास (d) = 2 x r cm
= 2 x 7 cm
= 14 cm
वर्गाकार रुमाल की प्रत्येक भुजा = 3 x प्रत्येक वृत्त का व्यास
= 3 x 14 cm = 42 cm
रुमाल के 9 वृत्ताकार डिज़ाइनों का क्षेत्रफल 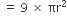
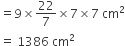
वर्गाकार रुमाल का क्षेत्रफल = भुजा x भुजा
= 42 x 42 cm2 = 1764 cm2
अत: वृत्ताकार डिज़ाइनों को छोड़कर शेष रुमाल का क्षेत्रफल = (1764 - 1386) cm2
= 378 cm2
आकृति में, OACB केंद्र O और त्रिज्या 3.5 cm वाले एक वृत्त का चतुर्थांश है। यदि OD = 2 cm है, तो निम्नलिखित के क्षेत्रफल ज्ञात कीजिए: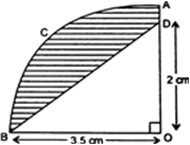
∴ चतुर्थांश OACB का क्षेत्रफल
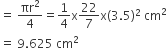
(ii) अब, समकोण
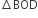 का क्षेत्रफल
का क्षेत्रफल 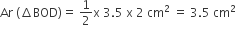
अत: आकृति के छायांकित भाग का क्षेत्रफल = (चतुर्थांश OACB -
 ) का क्षेत्रफल
) का क्षेत्रफल = (9.625 cm2 - 3.5)cm2
= 6.125 cm2.
आकृति में, एक चतुर्थांश OPBQ के अंतर्गत एक वर्ग OABC बना हुआ है। यदि OA = 20cm है, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। ( लीजिए।)
लीजिए।)
यहाँ पर, वर्ग OABC में, भुजा OA = भुजा AB = 20 cm
वर्ग OABC का क्षेत्रफल = भुजा x भुजा
= 20 x 20 cm2 = 400 cm2
चतुर्थांश OPBQ की त्रिज्या (OB) = 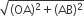
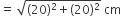

चतुर्थांश OPBQ का क्षेत्रफल = 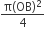
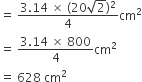
अत: आकृति के छायांकित भाग का क्षेत्रफल = (चतुर्थांश OPBQ - वर्ग OABC) का क्षेत्रफल
= (628 - 400) cm2
= 228 cm2
AB और CD केंद्र तथा त्रिज्याओं 21cm और 7cm वाले दो सकेंद्रिय वृतों के क्रमश: दो चाप हैं (देखिए आकृति)। यदि, तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। 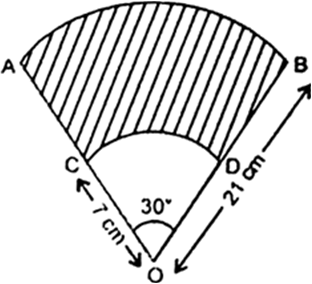
माना r1 = 7 cm (त्रिज्यखंड OCD के लिए) and r2 = 21 cm (त्रिज्यखंड OAB के लिए)
तथा 
त्रिज्यखंड OCD का क्षेत्रफल
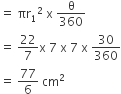
त्रिज्यखंड OAB का क्षेत्रफल
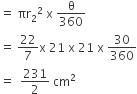
अत: आकृति में छायांकित भाग का क्षेत्रफल = (त्रिज्यखंड OAB - त्रिज्यखंड OCD) का क्षेत्रफल
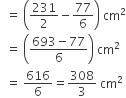
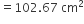
आकृति में , ABC त्रिज्या 14 cm वाले एक वृत्त का चतुर्थांश है तथा BC को व्यास मान कर एक अर्धवृत्त खींचा गया है। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।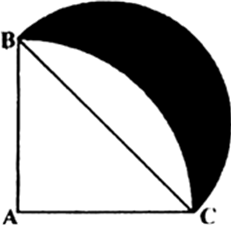
यहाँ पर, समकोण त्रिभुज ABC में, AB = AC = 14 cm
(वृत्त की त्रिज्या के समान)
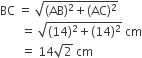
14 cm त्रिज्या वाले चतुर्थांश का क्षेत्रफल = 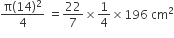
= 154 cm2
BC पर बने अर्धवृत की त्रिज्या = 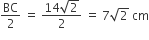
BC पर बने अर्धवृत का क्षेत्रफल = 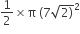
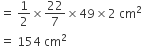
समकोण त्रिभुज ABC का क्षेत्रफल = 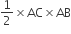
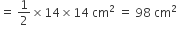
अत: आकृति में दर्शाए गए छायांकित भाग का क्षेत्रफल
= BC पर बने अर्धवृत का क्षेत्रफल - (चतुर्थांश का क्षेत्रफल -  का क्षेत्रफल)
का क्षेत्रफल)
= [154 - (154 - 98)] cm2
= [154 - 154 + 98] cm2 = 98 cm2
आकृति में, छायांकित डिज़ाइन का क्षेत्रफल ज्ञात कीजिए, जो 8 cm त्रिज्याओं वाले दो वृतों के चतुर्थांशों के बीच उभयनिष्ठ है। 
यहाँ पर,
आकृति में छायांकित डिज़ाइन का क्षेत्रफल = 2[चतुर्थांश ABD का क्षेत्रफल - समकोण  का क्षेत्रफल)
का क्षेत्रफल)
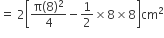
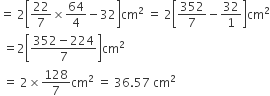
आकृति एक तीरंदाजी लक्ष्य को दर्शाती है, जिसमें केंद्र से बहार की और पाँच क्षेत्र GOLD, RED, BLUE, BLACK और WHITE चिन्हित हैं, जिनसे अंक अर्जित किए जा सकते हैं। GOLD अंक वाले क्षेत्र का व्यास 21 cm है तथा प्रत्येक अन्य पट्टी 10.5 cm चौड़ी है। अंक प्राप्त कराने वाले इन पाँचों क्षेत्रों में से प्रत्येक का क्षेत्रफल ज्ञात कीजिए। 
यहाँ पर,
GOLD अंक वाले वृत्त का व्यास = 21 cm
GOLD अंक वाले वृत्त की त्रिज्या (r) = 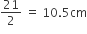
∴ GOLD अंक प्राप्त करने वाले क्षेत्र का क्षेत्रफल (A1) 
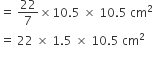
= 346.5 cm2 ...(i)
(GOLD + RED) अंक वाले वृत्त की त्रिज्या (r1) = (10.5 + 10.5)cm
= 2 x 10.5 cm
= 2 r cm
∴ RED अंक प्राप्त करने वाले क्षेत्र का क्षेत्रफल (A2) = 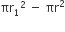
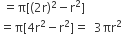
= 3 x 346.5 cm2 [समीकरण (i) से]
= 1039.5 cm2
(GOLD + RED + BLUE) अंक वाले वृत्त की त्रिज्या (r2) = (10.5+10.5+10.5)cm
= 3 x 10.5 cm = 3 r cm
∴ BLUE अंक प्राप्त करने वाले क्षेत्र का क्षेत्रफल (A3) = 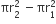
= 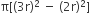
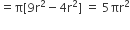
= 5 x 346.5 cm2 [समीकरण (i) से]
= 1732.5 cm2
(GOLD + RED + BLUE + BLACK) वाले वृत्त की त्रिज्या (r3) = 4 r cm
∴ BLACK अंक प्राप्त करने वाले क्षेत्र का क्षेत्रफल (A4) = 
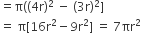
= 7 x 346.5 cm2 [समीकरण (i) से]
= 2425.5 cm2
(GOLD + RED + BLUE + BLACK + WHITE) अंक वाले वृत्त की त्रिज्या (r4) = 5 r cm
∴ WHITE अंक प्राप्त करने वाले क्षेत्र का क्षेत्रफल (A5) = 
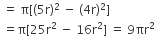
= 9 x 346.5 cm2 [समीकरण (i) से]
= 3118.5 cm2
आकृति 4 में, ABCD एक वर्ग है जिसकी भुजा 14 सेमी है। प्रत्येक भुजा को ब्यास मान कर अर्धवृत्त बनाए हैं। छायांकित भाग का क्षेत्रफल ज्ञात कीजिए।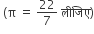
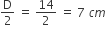
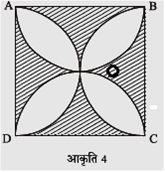
वृत्त का त्रिज्या, r = 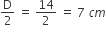
चूंकि सभी अर्धवृत्त का त्रिज्या एक जैसी है-
चारों अर्धवृत्त के क्षेत्रफल,
AOB + DOC + AOD + BOC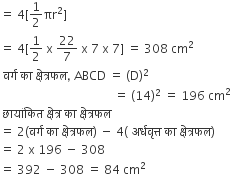
Sponsor Area
सिध्द कीजिए कि वृत्त जे बाह्म-बिंदु से वृत्त पर खींची गई स्पर्श रेखाएँ लम्बाई में सामान होती हैं।
दिया है,
PT और TQ दो स्पर्शरेखा हैं जो बाहरी बिंदु T से वृत्त C (O, r) में लिए गयीं हैं।
सिध्द कीजिए(to prove): 1. PT = TQ
2. ∠OTP = ∠OTQ
निर्माण: जोड़ना OT
प्रमाण(Proof): हम जानते हैं, कि वृत्त में स्पर्शरेखा संपर्क बिंदु के माध्यम से त्रिज्या के लिए लम्बवत्त है।
दी गई आकृति में, OACB एक वृत्त, जिसका केंद्र O तथा त्रिज्या 3.5 सेमी है, का चतुर्थांश है। यदि OD = 2 सेमी हो तो छायांकित भाग का क्षेत्रफल ज्ञात कीजिए। 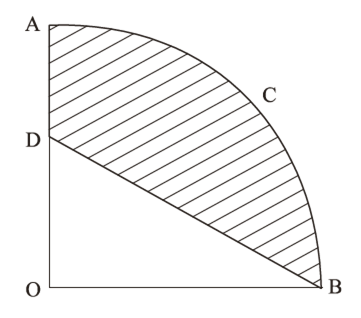

चूंकि OACB एक चतुर्भुज है, यह कोण O,
 कोण को घटा देगा।
कोण को घटा देगा।चतुर्भुज OACB का क्षेत्रफल,
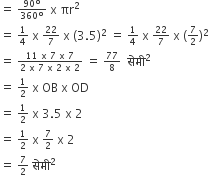
छायांकित क्षेत्र का क्षेत्रफल
= चतुर्भुज के क्षेत्र OACB - ΔOBD का क्षेत्रफल
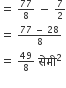
Mock Test Series
Sponsor Area
Sponsor Area






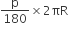
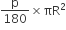
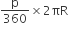
 =1.73 लीजिए)
=1.73 लीजिए)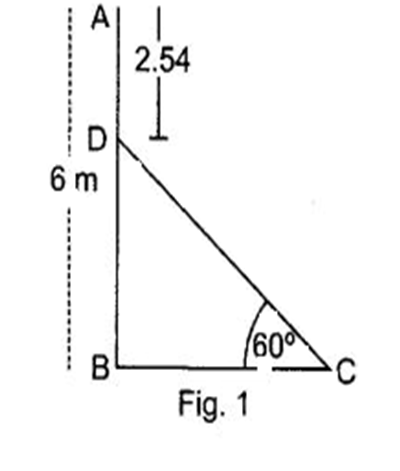
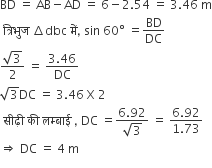

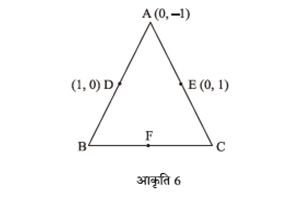
 ABC, जिसके शीर्ष A के निर्देशांक (0, -1) हैं तथा भुजाओं AB तथा AC के मध्य-बिंदुओं D तथा E के निर्देशांक क्रमशः (1, 0) तथा (0, 1) हैं। यदि F भुजा BC का मध्य-बिंदु हैं तो त्रिभुजों DEF तथा ABC के क्षेत्रफल ज्ञात कीजिए।
ABC, जिसके शीर्ष A के निर्देशांक (0, -1) हैं तथा भुजाओं AB तथा AC के मध्य-बिंदुओं D तथा E के निर्देशांक क्रमशः (1, 0) तथा (0, 1) हैं। यदि F भुजा BC का मध्य-बिंदु हैं तो त्रिभुजों DEF तथा ABC के क्षेत्रफल ज्ञात कीजिए।