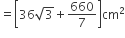वृतों से संबंधित क्षेत्रफल

Question

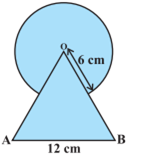
आकृति में, छायांकित भाग का क्षेत्रफल ज्ञात कीजिए, जहाँ भुजा 12 cm वाले एक समबाहु त्रिभुज OAB के शीर्ष O को केंद्र मान कर 6 cm त्रिज्या वाला एक वृत्तीय चाप खींचा गया है।

Solution

यहाँ पर, $increment AOB$ समबाहु त्रिभुज है।
   $therefore space space space space space angle AOB space equals space 60 degree$
[∵ समबाहु त्रिभुज का प्रत्येक कोण होता है।]
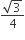समबाहु $increment AOB$ का क्षेत्रफल = $fraction numerator square root of 3 over denominator 4 end fraction$ x (भुजा)²
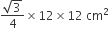
= $fraction numerator square root of 3 over denominator 4 end fraction cross times 12 cross times 12 space cm squared$
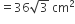
$equals 36 square root of 3 space cm squared$
वृत्त की त्रिज्या (r) = 6cm
वृत्त का क्षेत्रफल $equals πr squared$
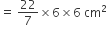
   $equals space 22 over 7 cross times 6 cross times 6 space cm squared$
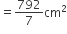
   $equals 792 over 7 cm squared$
सांझे(common) त्रिज्यखंड का क्षेत्रफल = 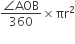$fraction numerator angle AOB over denominator 360 end fraction cross times πr squared$
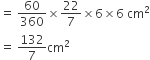
$equals space 60 over 360 cross times 22 over 7 cross times 6 cross times 6 space cm squared equals space 132 over 7 cm squared$
अत: आकृति में छायांकित भाग का कुल क्षेत्रफल $equals space open square brackets 36 square root of 3 plus 792 over 7 minus 132 over 7 close square brackets cm squared$
   $equals open square brackets 36 square root of 3 plus 660 over 7 close square brackets cm squared$

For Daily Free Study Material Join wiredfaculty

वृतों से संबंधित क्षेत्रफल

Some More Questions From वृतों से संबंधित क्षेत्रफल Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction