Sponsor Area
वृतों से संबंधित क्षेत्रफल
15cm त्रिज्या वाले एक वृत्त की कोई जीवा केंद्र पर 60° का कोण अंतरित करती है। संगत लघु और दीर्घ वृत्तखंडों के क्षेत्रफल ज्ञात कीजिए।
यहाँ पर,
r = 15 cm,  = 60°
= 60°
माना जीवा द्वारा केंद्र पर अंतरित कोण 
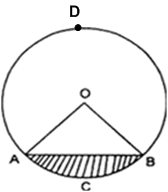
(i) लघु त्रिज्याखंड OACBO का क्षेत्रफल 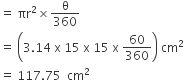
(ii) त्रिभुज OAB का क्षेत्रफल 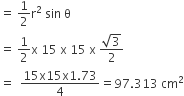
(iii) वृत्त का क्षेत्रफल = 
= 3.14 x 15 x 15 cm2
= 706.5 cm2
अब,
लघु वृत्तखंड ACB का क्षेत्रफल = (त्रिज्यखंड OACBO - त्रिभुज OAB) का क्षेत्रफल
= (117.75 - 97.313) cm2
= 20.4375 cm2
दीर्घ वृत्तखंड (ABDA) का क्षेत्रफल = वृत्त का क्षेत्रफल - लघुखंड का क्षेत्रफल
= (706.5 - 20.4375) cm2
= 686.0625 cm2
Some More Questions From वृतों से संबंधित क्षेत्रफल Chapter
Sponsor Area
Mock Test Series
Mock Test Series





