गणित Chapter 9 समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल
Sponsor Area
NCERT Solution For Class 9 गणित गणित
निम्नलिखित आकृतियों में से कौन-सी आकृतियाँ एक ही आधार और एक ही समान्तर रेखाओं के बीच स्थित हैं? ऐसे स्थिति में, उभयनिष्ठ आधार और दोनों समान्तर रेखाएँ लिखिए।


(i) 
उभयनिष्ठ आधार: DC
समांतर रेखाएँ : DC और AB
(ii) आकृतियाँ एक ही समांतर रेखाओं के बीच नहीं हैं।
(iii) 
उभयनिष्ठ आधार: RQ
समांतर रेखाएँ : RQ और PS
(iv)  और समांतर चतुर्भुज ABCD एक ही आधार पर नहीं हैं।
और समांतर चतुर्भुज ABCD एक ही आधार पर नहीं हैं।
(v) चतुर्भुज ABCD और ADQP
उभयनिष्ठ आधार: AD
समांतर रेखाएँ : AD और BQ
(vi) आकृतियाँ एक ही (या उभयनिष्ठ) आधार पर स्थित नहीं हैं।
आकृति में, ABCD एक समांतर चतुर्भुज है, AE ⊥ DC और CF ⊥ AD है। यदि AB = 16 सेमी., AE =8 सेमी. और CF = 10 सेमी. हैं, तो AD ज्ञात कीजिए।

ar(||gm ABCD) = AB x AE = 16 x 8 cm2 = 128 cm2 ...(1)
ar(||gm ABCD) = AD x CF = AD x 10 cm2 ...(2)
समीकरण (i) और (ii) के प्रयोग से
AD X 10 = 128
 AD = 12.8 सेमी.
AD = 12.8 सेमी.
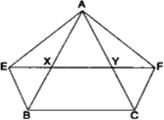
यदि E, F, G और H क्रमश: समान्तर चतुर्भुज ABCD की भुजाओं के मध्यबिंदु हैं, तो दर्शाइए कि  है।
है।

सिद्ध करना है:

प्रमाण:
 और ||gm BCHF एक ही आधार HF और एक ही समान्तर रेखाओं HF और BC के बीच स्थित हैं।
और ||gm BCHF एक ही आधार HF और एक ही समान्तर रेखाओं HF और BC के बीच स्थित हैं।∴
 ...(i)
...(i)और
 ...(ii)
...(ii)(i) और (ii) को जोड़ने पर


P और Q क्रमश:समान्तर चतुर्भुज ABCD की भुजाओं DC और AD पर स्थित बिंदु हैं। दर्शाइए कि ar(APB) = ar(BQC) है।
 और
और  बनते हैं।
बनते हैं।
सिद्ध करना हैं:

प्रमाण:
 और ||gm ABCD एक ही आधार AB और एक ही समान्तर रेखाओं AB और DC के बीच स्थित हैं।
और ||gm ABCD एक ही आधार AB और एक ही समान्तर रेखाओं AB और DC के बीच स्थित हैं।∴
 ...(i)
...(i)इसी प्रकार
 ...(ii)
...(ii)(i) और (ii) से

आकृति में, P समान्तर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि: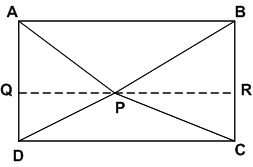
(1) (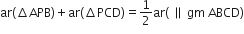
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
सिद्ध करना है: (i)
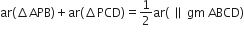
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
रचना: (i) P से होकर एक रेखा DC के समान्तर खींचों जो AD और BC को क्रमश: Q और R पर मिले।
प्रमाण:
 और ||gm ABRQ एक ही आधार AB और एक ही समान्तर रेखाओं AB और QR के बीच स्थित हैं।
और ||gm ABRQ एक ही आधार AB और एक ही समान्तर रेखाओं AB और QR के बीच स्थित हैं।∴
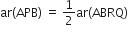 ...(i)
...(i)इस प्रकार ar (PCD) =
 ...(ii)
...(ii) (i) और (ii) से
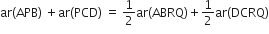
अत:
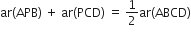
(ii) इसी प्रकार
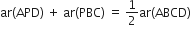
अत:

आकृति में PQRS और ABRS समांतर चतुर्भुज हैं तथा X भुजा BR पर स्थित कोई बिंदु है। दर्शाइए कि: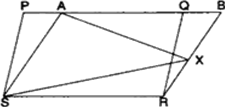
(i) ar(PQRS) = ar(ABRS)
(ii) 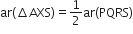
सिद्ध करना है: (i) ar(PQRS) = ar(ABRS)
(ii) ar(AXS) =

प्रमाण: (i) ||gms PQRS और ABRS एक आधार SR और एक ही समांतर रेखाओं SR और PB के बीच स्थित हैं।
∴ ar(PQRS) = ar(ABRS) ...(i)
(ii)
 और ||gm ABRS एक आधार AS और एक ही समांतर रेखाओं AS और RB के बीच स्थित हैं।
और ||gm ABRS एक आधार AS और एक ही समांतर रेखाओं AS और RB के बीच स्थित हैं।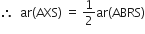 ...(ii)
...(ii)(i) और (ii) से,
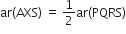
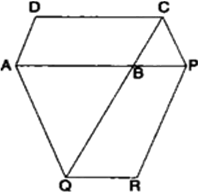
एक किसान के पास समान्तर चतुर्भुज PQRS के रूप का खेत था। उसने RS पर स्थित कोई बिंदु A लिया और उसे P और Q से मिला दिया। खेत कितने भागों में विभाजित हो गया है? इन भागों के आकार क्या हैं? वह किसान खेत में गेहूँ और दालें बराबर-बराबर भागों में अलग-अलग बोना चाहता है। वह ऐसा कैसे करे?
एक ||gm PQRS भुजा SR पर एक बिंदु A स्थित है। A को P और Q से मिलाया गया है। क्षेत्र को तीन भागों (i)  (ii)
(ii)  (iii)
(iii)  में बाँटा गया है। सभी भाग त्रिभुज हैं।
में बाँटा गया है। सभी भाग त्रिभुज हैं।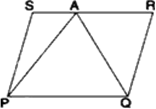
 और ||gm PQRS एक आधार PQ और एक ही समान्तर रेखाओं के बीच स्थित है।
और ||gm PQRS एक आधार PQ और एक ही समान्तर रेखाओं के बीच स्थित है।
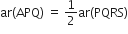 ...(i)
...(i)
∴ ar(ASP) + ar(APQ) + ar(AQR) = ar(PQRS)
ar(ASP) +  + ar(AQR) = ar(PQRS)
+ ar(AQR) = ar(PQRS)
∴ 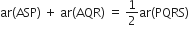 ...(ii)
...(ii)
(i) और (ii) से,
ar(APQ) = ar(ASP) + ar(AQR)
इस प्रकार, किसान को  में गेहूँ और अन्य दो त्रिभुजाओं में दालें या दाल
में गेहूँ और अन्य दो त्रिभुजाओं में दालें या दाल  में और गेहूँ अन्य दो त्रिभुजों में बोनी चाहिए।
में और गेहूँ अन्य दो त्रिभुजों में बोनी चाहिए।
आकृति में  की एक माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि ar(ABE) = ar(ACE) है।
की एक माध्यिका AD पर स्थित E कोई बिंदु है। दर्शाइए कि ar(ABE) = ar(ACE) है।
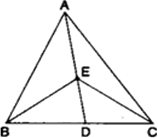
ज्ञात है:  की एक माध्यिका AD है और E, AD का एक बिंदु है।
की एक माध्यिका AD है और E, AD का एक बिंदु है।
सिद्ध करना है: 
प्रमाण:  में AD एक माध्यिका है।
में AD एक माध्यिका है। ...(i)
...(i)
[∴ माध्यिका एक त्रिभुज को दो समान क्षेत्रफलों वाली त्रिभुजों में विभाजित करती है।]
इसी प्रकार  में, ED एक माध्यिका है।
में, ED एक माध्यिका है।
∴  ...(ii)
...(ii)
(i) में से (ii) को घटाने पर 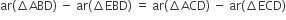
अत: 
 में, E माध्यिका AD का मध्यबिंदु है। दर्शाइए कि ar(BED) =
में, E माध्यिका AD का मध्यबिंदु है। दर्शाइए कि ar(BED) = 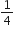 ar(ABC) है।
ar(ABC) है।
 में,E माध्यिका AD का मध्यबिंदु है।
में,E माध्यिका AD का मध्यबिंदु है।सिद्ध करना है:
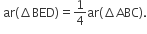
 में AD एक माध्यिका है। चूँकि माध्यिका
में AD एक माध्यिका है। चूँकि माध्यिका  को समान क्षेत्रफलों वाली दो त्रिभुजाओं में विभाजित करती है।
को समान क्षेत्रफलों वाली दो त्रिभुजाओं में विभाजित करती है।∴ ar.(ABD) = ar. (ACD)
इस प्रकार ar.(ABD) =
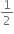 ar. (ACD) ...(i)
ar. (ACD) ...(i)इसी प्रकार
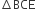 में EB एक माध्यिका है।
में EB एक माध्यिका है। ∴ ar.(BED) =
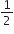 (ABD) ...(ii)
(ABD) ...(ii)(i) और (ii)
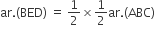 से,
से, 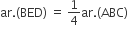
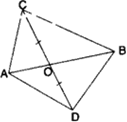
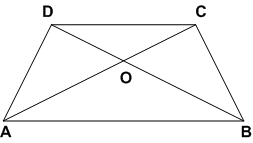
दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाटँते हैं।
ज्ञात है: चतुर्भुज ABCD के विकर्ण AC और BD बिंदु O पर प्रतिच्छेद करते हैं। इस प्रकार चार त्रिभुजें AOD, AOB, COB और COD बनते हैं।
सिद्ध करना हैं: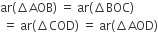
प्रमाण: चूँकि एक ||gm के विकर्ण परस्पर समद्विभाजित करते हैं।
∴ O, मध्यबिंदु है (AC और BD का)
अब, ΔABC में OB एक माध्यिका है।
∴ ar(ΔAOB) = ar(ΔBOC) ...(i)
[∵ माध्यिका Δ को दो समान क्षेत्रफलों वाली Δ में बांटती हैं]
इसी प्रकार,
ar(ΔBOC) = ar(ΔCOD) ...(ii)
और ar(ΔCOD) = ar(ΔAOD) ...(iii)
(i), (ii) और (iii) से,
ar(ΔAOB) = ar(ΔBOC)
= ar(ΔCOD)
= ar(ΔAOD)
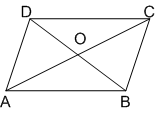
आकृति में, ABC और ABD एक ही आधार AB पर बने दो त्रिभुज हैं। यदि रेखाखण्ड CD रेखाखण्ड
AB से बिंदु O पर समद्विभाजित होता है, तो दर्शाइए कि:
ar(AABC) = ar(ΔABD).है।
सिद्ध करना है: ar(ΔABC) = ar(ΔABD).
प्रमाण: ΔACD में OA एक माध्यिका है।
∴ ar(OAC) = ar(OAD) ...(i)
इसी प्रकार, ΔBCD में, OB एक माध्यिका है।
∴ ar(OBC) = ar(OBD) ...(ii)
(i) और (ii) से
ar(OAC) + ar(OBC) = ar(OAD) + ar(OBD)
अत: ar(ABC) = ar(ABD)
D, E और F क्रमश:त्रिभुज ABC की भुजाओं और के मध्य-बिंदु हैं। दर्शाइए कि
(i) BDEF एक समांतर चतुर्भुज है
(ii) ar(DEF) = 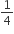 ar(ABC)
ar(ABC)
(iii) ar(BDEF) = 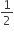 ar(ABC)
ar(ABC)
 में D, E और F क्रमश: भुजाओं BC, CA और AB के मध्यबिंदु हैं।
में D, E और F क्रमश: भुजाओं BC, CA और AB के मध्यबिंदु हैं। सिद्ध करना: (i) BDEF एक ||gm है।
(ii) ar(ΔDEF) =
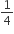 ar(ΔABC)
ar(ΔABC)(iii) ar(BDEF) =
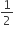 ar(ABC)
ar(ABC)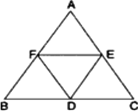
प्रमाण: (i) ΔABC में F और E क्रमश: भुजाओं AB और AC के मध्यबिंदु हैं।
∴ FE || BC या BD ...(i)
[मध्यबिंदु प्रमेय]
पुन: ΔABC में E और D क्रमश: भुजाओं AC और BC के मध्यबिंदु हैं।
∴ DE || BF (मध्यबिंदु प्रमेय) ...(ii)
(i) और (ii) से,
BDEF एक समांतर चतुर्भुज है।
(ii) ||gm BDEF में,

और

∴ ar(AFE) = ar(DEC) = ar(DEF) = ar(BDF)
अत: ar(ΔDEF) =
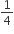 ar(ΔABC)
ar(ΔABC)(iii) (i) और (ii) से
ar (BDEF) =
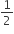 ar(ABC)
ar(ABC)आकृति में, चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि OB = OD है। यदि AB = CD हो, तो दर्शाइए कि:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB या ABCD एक समांतर चतुर्भुज है।
[संकेत: D और B से AC पर लम्ब खींचिए।]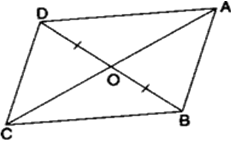
सिद्ध करना है: (i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB
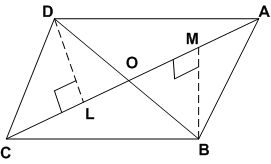
रचना: AC पर D और B से क्रमश: DL और BM लम्ब खींचों।
प्रमाण: (i) ΔDOL और ΔBMO से
 (प्रत्येक =
(प्रत्येक =  )
)OB = OD (ज्ञात है)
 [शीर्षभिमुख कोण]
[शीर्षभिमुख कोण]∴
 (AAS नियम)
(AAS नियम)इस प्रकार, DL = MB (CPCT) ...(i)
अब, ar(ΔDOC) =
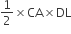 ...(ii)
...(ii)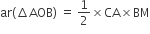 ...(iii)
...(iii)या
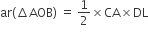 ...(iv)
...(iv)(ii) और (iv) से,
ar (ΔDOC) = ar(ΔAOB)
(ii) अब ar (ΔDOC) = ar(ΔAOB)
दोनों ओर ar(ΔBOC) जोड़ने पर
ar(ΔDOC) + ar(ΔBOC) = ar(ΔAOB) +ar(ΔBOC)
अत: ar(ΔDCB) = ar(ΔABC)
चूँकि ΔDCB और ΔABC एक ही आधार पर स्थित हैं और उनके क्षेत्रफल समान हैं।
इसलिए

बिंदु D और E क्रमश: ΔABC की भुजाओं AB और AC पर इस प्रकार स्थित हैं कि
ar(ΔDBC) = ar(ΔEBC) है। दर्शाइए कि DE || BC है।
ज्ञात है: ΔABC में भुजाओं AB और AC पर क्रमश: बिंदु D और E स्थित हैं और ar(ΔDBC) = ar(ΔEBC).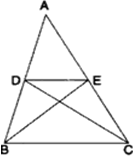
सिद्ध करना है: DE || BC है।
प्रमाण: चूँकि ar (ΔDEC) = ar(ΔEDB) और ΔDBC और ΔEBC एक ही आधार पर स्थित हैं इसलिए एक ही सामन्तर रेखाओं DE || BC के बीच स्थित हैं।
XY त्रिभुज ABC की भुजा BC के समांतर एक रेखा है। यदि BE || AC और CF || AB रेखा XY से क्रमश:E और F पर मिलती हैं, तो दर्शाइए कि:
ar(ΔABE) = ar(ΔACF).
BE || AC और CF || AB, XY को क्रमश: E और F पर मिलते हैं।
सिद्ध करना हैं:
ar(ΔABE) = ar(ΔACF).
प्रमाण: ∵ ΔABE और ||gm BCYE एक ही आधार BE और एक ही समांतर रेखाओं BE और AC के बीच स्थित हैं।
∴ ar(ΔABE) =
 ar (||gm BCYE) ...(i)
ar (||gm BCYE) ...(i)इसी प्रकार,
ar(ΔACF) =
 ar(|| gm BCFX) ...(ii)
ar(|| gm BCFX) ...(ii)परन्तु ||gm BCYE और ||gm BCFX एक ही आधार BC और एक ही समांतर रेखाओं BC और EF के बीच स्थित हैं।
∴ ar(||gm BCYE) = ar(||gm BCFX) ...(iii)
(i), (ii) और (iii) से
∴ ar(ΔABE) = ar(ΔACF).
समांतर चतुर्भुज ABCD की एक भुजा AB को बिंदु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है। दर्शाइए कि:
ar(ABCD) = ar(PBQR) है।
सिद्ध करना है: ar(ABCD) = ar(PBQR)
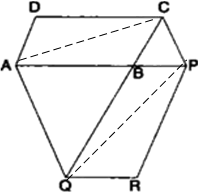
रचना: A और C को मिलाओ। P और Q को भी मिलाओ।
प्रमाण: ΔACQ और ΔAPQ एक ही आधार और एक ही समान्तर रेखाओं AQ तथा CP के बिच स्थित हैं।
∴ ar.(ΔACQ) = ar(ΔAPQ)
अब, दोनों ओर से ar(ΔABQ) घटाने पर
ar.(ΔACQ) - ar(ΔABQ) = ar.(ΔAPQ) - ar(ΔABQ)
या ar(ΔABC) घटाने पर, ...(i)
हम जानते हैं कि ||gm का विकर्ण इसे समान क्षेत्रफल वाले दो त्रिभुजाओं में बांटता है।
∴ ||gm ABCD में,
ar.(ΔABC) =
 ar. (||gm ABCD) ...(ii)
ar. (||gm ABCD) ...(ii)और ||gm QRPB में,
ar.(ΔBQP) =
 ar.(||gm BPQR) ...(iii)
ar.(||gm BPQR) ...(iii)(i), (ii) और (iii) से,
∴ ar(ABCD) = ar(PBQR)
एक समलम्ब ABCD, जिसमें AB||CD है, के विकर्ण AC और BD परस्पर O पर प्रतिच्छेद करते हैं।दर्शाइए कि ar(ΔAOD) = ar(ΔBOC) है।
सिद्ध करना है: ar(ΔAOD) = ar(ΔBOC)
प्रमाण: ΔACD और ΔBCD एक ही आधार CD और एक ही समांतर रेखाओं AB और DC के बीच स्थित हैं।
∴ ar(ΔACD) = ar(ΔBCD) ...(i)
दोनों ओर से ar(ΔCOD) घटाने पर,
ar(ΔACD) - ar(ΔCOD) = ar(ΔBCD) - ar(ΔCOD)
 ar(ΔAOD) = ar(ΔBOC).
ar(ΔAOD) = ar(ΔBOC).Sponsor Area
आकृति में, ABCDE एक पंचभुज है। B से होकर AC के समान्तर खींची गई रेखा बढ़ाई गई DC को F पर मिलती है। दर्शाइए कि: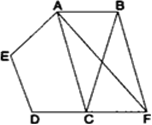
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(AEDF) = ar(ABCDE)
सिद्ध करना है: (i) ar(ΔACB) = ar(ΔACF)
(ii) ar(AEDF) = ar(ABCDE)
प्रमाण: (i) ΔACB और ΔACF एक ही आधार AC पर और एक ही समान्तर रेखाओं AC और BF के बीच स्थित हैं।
∴ ar(ΔACB) = ar(ΔACF)
(ii) अब, ar(ΔACB) = ar(ΔACF)
(ऊपर सिद्ध किया है)
दोनों ओर ar(ACDE) जोड़ने पर
ar(ΔACB) + ar(ACDE) = ar(ΔACF) + ar.(ACDE)
ar(ABCDE) = ar(AEDF)
अत: ar(AEDF) = ar(ABCDE).
गाँव के एक निवासी इतवारी के पास एक चतुर्भुजाकार भूखंड था। उस गाँव की ग्राम पंचायत ने उसके भूखंड के एक कोने से उसका कुछ भाग लेने का निर्णय लिया ताकि वहाँ एक स्वास्थ्य केंद्र का निर्माण कराया जा सके। इतवारी इस प्रस्ताव को इस प्रतिबन्ध के साथ स्वीकार कर लेता है कि उसे इस भाग के बदले उसी भूखंड के सलंग्न एक भाग ऐसे दे दिया जाए कि उसका भूखंड त्रिभुजाकार हो जाए। स्पष्ट कीजिए कि इस प्रस्ताव को किस प्रकार कार्यान्वित किया जा सकता है।
माना किसान का भूखंड नीचे दी गई आकृति का है, जो चतुर्भुज ABCD के रूप में है। इसे एक समान क्षेत्रफल की त्रिभुज में बदलना है।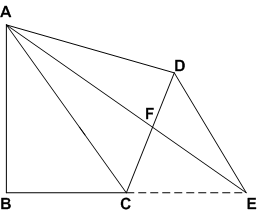
रचना: BC को E तक बढ़ाओं ताकि DE || AC हो।
A और E को मिलाओ जो BC के बढ़ाए गए भाग से E पर मिले।
प्रमाण: चूँकि ΔDAC और ΔEAC एक ही आधार AC और एक ही समांतर रेखाओं AC और DE के बीच स्थित हैं।
∴ ar.ΔDAC = ar.ΔEAC
दोनों ओर ar.(ΔABC) जोड़ने पर,
ar(ABCD) = ar (ΔABE)
अत: स्पष्ट है कि स्वास्थ्य केंद्र के लिए दिया गया भूखंड = ar. (ΔADF)
∴ उक्त भूखंड के बदले में किसान को दिया गया भूखंड = ar. (ΔCEF)
एक समलम्ब ABCD में AB || DC है। AC के समान्तर एक रेखा AB को X पर और BC को Y पर प्रतिच्छेद करती है। सिद्ध कीजिए कि:
ar(ΔADX) = ar(ΔACY) है।
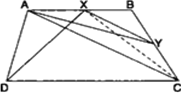
सिद्ध करना है: ar(ΔADX) = ar(ΔACY) है।
रचना: C और X को मिलाओ तथा D और X को मिलाओ।
प्रमाण: ΔADX और ΔACX एक आधार AX तथा एक ही समान्तर रेखाओं AX और DC के बीच स्थित हैं।
∴ ar(ΔADX) = ar(ΔACX)
पुनः ΔACX और ΔACY एक ही आधार और एक ही समान्तर रेखाओं AC और XY के बीच स्थित हैं।
∴ ar(ΔACX) = ar(ΔACY)
(i) और (ii) से,
अत: ar(ΔADX) = ar(ΔACY).
आकृति में, AP || BQ || CR है। सिद्ध कीजिए कि ar(AQC) = ar(PBR).
ar(ΔAQC) = ar(ΔPBR).
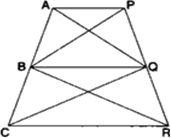
सिद्ध करना है:
ar(ΔAQC) = ar(ΔPBR)
प्रमाण: ΔABQ और ΔPBQ एक आधार BQ पर और एक ही समांतर रेखाओं AP और BQ के बीच स्थित हैं।
∴ ar(ΔABQ) = ar(ΔPBQ) ...(i)
पुन: ΔBQC और ΔQBR एक ही आधार BQ और एक ही समांतर रेखाओं के बीच स्थित हैं।
∴ ar(ΔBQC) = ar(ΔQBR) ...(ii)
(i) और (ii) को जोड़ने पर,
ar(ΔABQ) + ar (BQC) = ar(PBQ) + ar(QBR)
 ar(ΔAQC) = ar(ΔPBR).
ar(ΔAQC) = ar(ΔPBR).
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिंदु O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD) = ar(ΔBOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
ar(ΔAOD) = ar(ΔBOC)
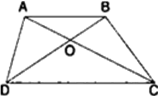
सिद्ध करना है: ABCD एक समलम्ब है।
प्रमाण: ar(ΔAOD) = ar(ΔBOC) (ज्ञात है)
दोनों और ar.(ΔCOD) जोड़ने पर,
ar(ΔAOD) + ar(ΔCOD) = ar(ΔBOC) + ar (ΔCOD)
∴ ar(ΔACD) = ar(ΔBCD)
चूँकि ΔACD और ΔBCD एक ही आधार CD पर स्थित हैं और उनके क्षेत्रफल समान हैं।
∴ AB || CD
अब, चतुर्भुज ABCD की सम्मुख भुजाएँ समान्तर हैं।
∴ ABCD एक समलम्ब है।
आकृति में, ar(ΔDRC) = ar(ΔDPC) और ar(ΔBDP) = ar(ΔARC) हैं। दर्शाइए कि दोनों चतुर्भुज ABCD और DCPR समलम्ब हैं।
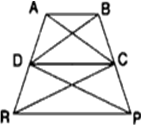
ar(ΔDRC) = ar(ΔDPC)
और ar(ΔBDP) = ar(ΔARC)
सिद्ध करना है: (i) चतुर्भुज DCPR एक समलम्ब है।
(ii) चतुर्भुज ABCD एक समलम्ब है।
प्रमाण: (i) ar(ΔDRC) = ar(ΔDPC)
ar(ΔDRC) और (ΔDPC) एक ही आधार DC पर स्थित हैं और उनके क्षेत्रफल भी समान हैं।
∴ DC || RP
अत: DCPR एक समलम्ब है।
अब,
ar(ΔBDP) = ar(ΔARC)
या ar(ΔBCD) + ar (ΔDPC) = ar(ΔADC) + ar(ΔDRC)
∴ ar(ΔBCD) = ar(ΔADC)
अब, ΔACD और ΔADC एक ही आधार DC पर स्थित हैं और उनके क्षेत्रफल समान हैं।
∴ AB || DC
अत: ABCD एक समलम्ब है।
एक समान्तर चतुर्भुज ABCD और आयत ABEF एक ही आधार पर स्थित हैं और उनके क्षेत्रफल बराबर हैं। दर्शाइए कि समान्तर चतुर्भुज का परिमाप आयत के परिमाप से अधिक है।

सिद्ध करना है:
(||gm ABCD का परिमाप) > (आयत ABEF का परिमाप) अर्थात्
AB + BC + CD + DA > AB + BE + EF + AF.
प्रमाण:
 में,
में, 
∴ DA > FA ...(i)
और
 में
में 
∴ BC > BE ...(ii)
तथा AB = EF ...(iii)
(आयत की सम्मुख भुजाएँ)
CD = AB
(|| gm की सम्मुख भुजाएँ)
(i), (ii), (iii) और (iv) से
DA + BC + AB + CD > FA + BE + EF + AB
अत: AB + BC + CD + DA > AB + BE + EF + AF.
आकृति में, भुजा BC पर दो बिंदु D और E इस प्रकार स्थित हैं कि BD=DE=EC हैं। दर्शाइए कि: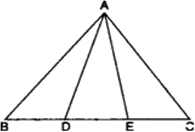
ar(ΔABD) = ar(ΔADE) = ar(ΔAEC).
क्या आप अब उस प्रश्न का उत्तर दे सकते हैं, जो आपने इस अध्याय की 'भूमिका' में छोड़ दिया था कि "क्या बुधिया का खेत वास्तव में बराबर क्षेत्रफलों वाले तीन भागों में विभाजित हो गया है"?
[टिप्पणी: ध्यान दीजिए कि BD = DE = EC लेने से ΔABC तीन त्रिभुजों ABD, ADE और AEC में विभाजित हो जाता है जिनके क्षेत्रफल बराबर हैं। इसी प्रकार, BC को n बराबर भागों में विभाजित करके और इस भुजा को विभाजित करने वाले बिंदुओं को सम्मुख शीर्ष से मिला कर आप इस त्रिभुज को बराबर क्षेत्रफलों वाले n त्रिभुजों में विभाजित कर सकते हैं]
 में, D और E भुजा BC पर दो बिंदु इस प्रकार हैं कि BD = DE = EC.
में, D और E भुजा BC पर दो बिंदु इस प्रकार हैं कि BD = DE = EC.सिद्ध करना है: ar(ΔABD) = ar(ΔADE) = ar(ΔAEC)
रचना: AM ⊥ BC खींचों।
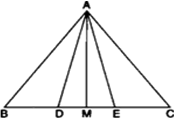
प्रमाण: (ΔABC) =
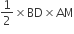
ar(ΔADE) =

और ar(ΔAEC) =
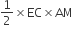
चूँकि BD = DE = EC
अत: ar(ΔABD) = ar(ΔADE) = ar(ΔAEC)
आकृति में, ABCD, DCFE और ABFE समांतर चतुर्भुज हैं। दर्शाइए कि:
ar(ΔADE) = ar(ΔBCF).

सिद्ध करना है: ar(ΔADE) = ar(ΔBCF).
प्रमाण: ΔADE और ΔBCF में,
AE = BF
AD = BC (||gm की सम्मुख भुजाएँ)
DE = CF
अत:
 (SSS नियम)
(SSS नियम)चूँकि सर्वांगसम त्रिभुजों के क्षेत्रफल समान होते हैं।
अत: (ΔADE) = ar(ΔBCF).
आकृति में, ABCD एक समान्तर चतुर्भुज है और BC को एक बिंदु Q तक इस प्रकार बढ़ाया गया है कि AD = CQ है। यदि AQ भुजा DC को P पर प्रतिच्छेद करती है, तो दर्शाइए कि: ar(ΔBPC) = ar(ΔDPQ).
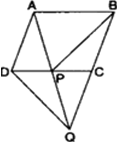
ज्ञात है: ABCD एक ||gm है। BC को Q तक बढ़ाया गया है कि AD = CQ. AQ, DC को P पर प्रतिच्छेद करता है।
सिद्ध करना है: ar(ΔBPC) = ar(ΔDPQ).
रचना: A और C को मिलाओ।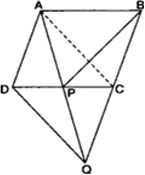
प्रमाण: AD = CQ
और AD || CQ
∴ ADQC एक || gm है।
∴ ar(ΔPDQ) = ar(ΔPCQ)
||gm के विकर्ण इस समान क्षेत्रफल वाली 4 त्रिभुजों में बांटते हैं।
अत: ar(ΔDPQ) = ar(ΔPCQ) ...(i)
और PBQ में, BC = AD = CQ
∴ BC = CQ
∴ ar(ΔPCQ) = ar(ΔBPC) ...(ii)
(i) और (ii) से
ar(ΔBPC) = ar(ΔDPQ)
आकृति में, ABC और BDE दो समबाहु त्रिभुज इस प्रकार हैं कि D भुजा BC का मध्य-बिंदु है। यदि AE भुजा BC को F पर प्रतिच्छेद करती है, तो दर्शाइए कि:
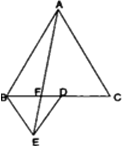
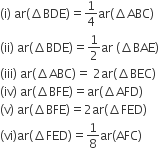
सिद्ध करना है:
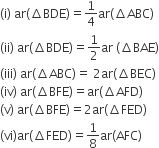
रचना: E और C तथा A और D को मिलाओ।
प्रमाण: (i) माना
 की भुजा = x
की भुजा = x∴
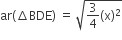
अब,
 की भुजा = 2x
की भुजा = 2x∴
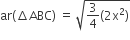
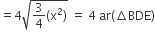
अत;
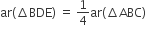
(ii)
 (प्रत्येक =
(प्रत्येक =  )
)परन्तु ये एकान्तर कोण हैं।
∴ BE || AC
अब,
 और
और  एक ही आधार BE और एक ही समांतर रेखाओं AC और BE के बीच स्थित हैं।
एक ही आधार BE और एक ही समांतर रेखाओं AC और BE के बीच स्थित हैं।∴
 ...(i)
...(i)पुन;
 मे, D, BC का मध्य बिंदु है।
मे, D, BC का मध्य बिंदु है।∴
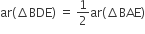 ...(ii)
...(ii)(iii) चूँकि एक माध्यिका Δ को दो समान क्षेत्रफल वाली त्रिभुजाओं में बाटँती है।
∴


परन्तु
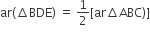 ...(ii)
...(ii)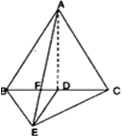
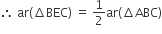
(iv)

परन्तु ये एकान्तर कोण का युग्म है।
∴ AB || DE
अब,
 और
और  एक ही आधार ED पर स्थित हैं और एक ही समांतर रेखाओं AB और DE के बीच स्थित हैं।
एक ही आधार ED पर स्थित हैं और एक ही समांतर रेखाओं AB और DE के बीच स्थित हैं।∴

दोनों और से
 को घटाने पर,
को घटाने पर,ar(ΔADE) - ar(ΔFED) = ar(ΔBED) - ar(ΔFED)
ar(ΔAFD) = ar(ΔBFE)
(v) ar(ΔBFE) = ar(ΔAFC)
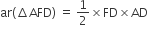 ...(A)
...(A)तथा ar(ΔBFE) =
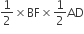
∴
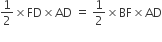
2FD = BF
अब, ar(ΔFED) =
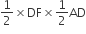
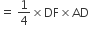 ...(B)
...(B)(A) और (B) से
ar(ΔAFD) = ar(ΔFED)
(vi) चूँकि 2FD = BF
∴ BD = x होने पर
BF =
 , FD =
, FD = 
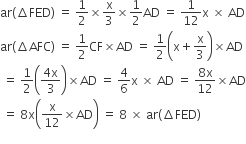
अत:
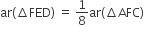
चतुर्भुज ABCD के विकर्ण AC और BD परस्पर P पर प्रतिच्छेद करते हैं। दर्शाइए कि:
ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).
सिद्ध करना हैं: ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).
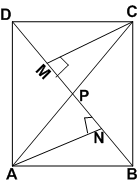
प्रमाण: ar(ΔAPB) =
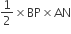 ...(i)
...(i)और ar(ΔAPD)
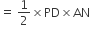 ...(ii)
...(ii)तथा ar(ΔCPD) =
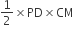
और ar(ΔBPC) =
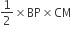
बायाँ पक्ष = ar(ΔAPB) x ar(ΔCPD)
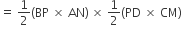
दायाँ पक्ष = ar(ΔAPD) x ar(ΔBPC)
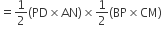
अत; बायाँ पक्ष = दायाँ पक्ष
P और Q क्रमश: त्रिभुज ABC की भुजाओं AB और BC के मध्यबिंदु हैं तथा R रेखाखण्ड AP का मध्यबिंदु है, दर्शाइए कि
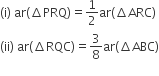
(iii) ar(ΔPBQ) = ar(ΔARC).
रचना: AQ और CP को मिलाएं।
सिद्ध करना है:
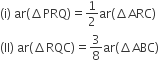
(iii) ar(ΔPBQ) = ar(ΔARC)
प्रमाण: P, AB का मध्यबिंदु है।
∴ PC एक माध्यिका है।

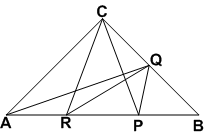
अब, ΔPAC में, CR एक माध्यिका है।
∴ ar(ΔPRC) = ar(ΔARC)
 ...(i)
...(i)या ar(ΔARC) =


∵ CR,
 की माध्यिका है।
की माध्यिका है।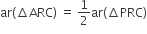
 ...(ii)
...(ii)तथा

 ...(iii)
...(iii)अब
 में, PQ एक माध्यिका है।
में, PQ एक माध्यिका है।∴

 ... (iv)
... (iv)
 ...(v)
...(v)(i)

[एक ही आधार PQ पर स्थित दो त्रिभुज तथा PQ || AC है]

[समी. (iv) से]
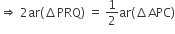
[समी. (i), (iii) से]

[समी. (ii) से]
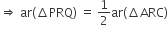
[भाग (i) सिद्ध हुआ]
(ii)
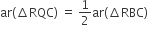
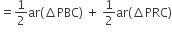

[समी. (i) तथा (ii) से]
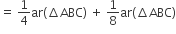
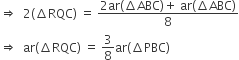
[भाग (ii) सिद्ध हुआ]
(iii)
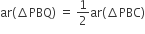 [समी. (iv) से]
[समी. (iv) से] ...(i)
...(i)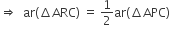
 ...(ii)
...(ii)समी. (i) तथा (ii) से

[भाग (iii) सिद्ध हुआ]
आकृति में, ABC एक समकोण त्रिभुज है जिसका कोण A समकोण है। BCED, ACFG और ABMN क्रमश: भुजाओं BC, CA और AB पर बने वर्ग हैं। रेखाखण्ड AX ⊥ DE भुजा BC को बिंदु Y पर मिलता है। दर्शाइए कि:
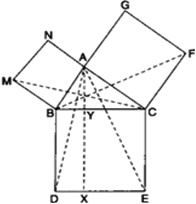
(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ΔABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(ΔFCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG).
ज्ञात है: ΔABC और  वर्ग BCED, ACFG और ABMN क्रमश: भुजाओं BC, CA और AB पर बने वर्ग हैं। AX ⊥ DE जो कि BC को Y पर काटती है।
वर्ग BCED, ACFG और ABMN क्रमश: भुजाओं BC, CA और AB पर बने वर्ग हैं। AX ⊥ DE जो कि BC को Y पर काटती है।
सिद्ध करना है:
(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ΔABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(ΔFCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG).
प्रमाण: (i) ΔMBC और ΔABD में,
MB = AB (वर्ग की भुजाएँ)
BC = BD (वर्ग की भुजाएँ)


 (SAS नियम)
(SAS नियम)
(ii) ar(ΔMBC) = ar(ΔABC) ...(i)
[सर्वांगसम त्रिभुजों के ar. समान हैं]
अब आयत BYXD और ΔABD एक ही आधार और एक ही || रेखाओं के बीच हैं।
या ar(BYXD) =2 ar(ABD) ...(ii)
(i) और (ii) से हम प्राप्त करते हैं
ar(BYXD) =2 ar(MBC) ...(iii)
(iii) पुन: वर्ग ABMN और ΔMBC एक ही आधार और एक ही || रेखाओं के बीच हैं।
2ar(MBC) = ar(ABMN) ...(iv)
(iii) और (iv) से,
ar(BXYD) = ar(ABMN) ...(A)
(iv) ΔFCB और ΔACE में,
BC = CE (आयत की भुजाएँ)
CF = AC (वर्ग की भुजाएँ)


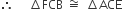 (SAS नियम)
(SAS नियम)
(v) 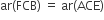 ...(v)
...(v)
[∵ सर्वांगसम त्रिभुजों के ar. समान हैं]
ΔACE और आयात CYXE एक ही आधार CE पर और एक ही समान्तर रेखाओं AX और CE के बीच स्थित हैं।
∴ ar(CYXE) = 2ar(ACE) ...(vi)
(v) और (vi) से
ar(CYXE) = 2ar(FCB) ...(vii)
(vi) ΔBCF और वर्ग एक ही आधार AC और एक ही || रेखाओं CF और BAG के बीच स्थित हैं। ∴ ar(ACFG) = 2ar(FCB) ...(viii)
(v), (vi), (vii) और (viii) से
ar(CYXE) = ar(ACFG) ...(ix)
(vii) (viii) और (ix) को जोड़ने पर
ar(BXYD) + ar(CYXE) = ar(ABMN) + ar(ACFG)
अत:ar(BCED) = ar(ABMN) + ar(ACFG)
Mock Test Series
Sponsor Area
Sponsor Area





