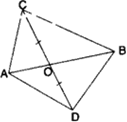
Question
आकृति में, P समान्तर चतुर्भुज ABCD के अभ्यंतर में स्थित कोई बिंदु है। दर्शाइए कि: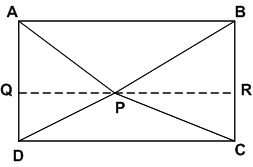
(1) (
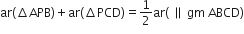
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
Solution
ज्ञात है: ||gm ABCD के अभ्यंतर एक बिंदु P स्थित है।
सिद्ध करना है: (i)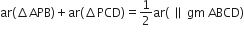
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
रचना: (i) P से होकर एक रेखा DC के समान्तर खींचों जो AD और BC को क्रमश: Q और R पर मिले।
प्रमाण:
और ||gm ABRQ एक ही आधार AB और एक ही समान्तर रेखाओं AB और QR के बीच स्थित हैं।
∴
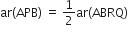...(i)
इस प्रकार ar (PCD) =
...(ii)
(i) और (ii) से
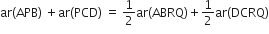
अत:
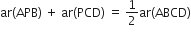
(ii) इसी प्रकार
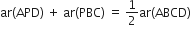
अत:
सिद्ध करना है: (i)
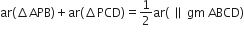
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
रचना: (i) P से होकर एक रेखा DC के समान्तर खींचों जो AD और BC को क्रमश: Q और R पर मिले।
प्रमाण:
और ||gm ABRQ एक ही आधार AB और एक ही समान्तर रेखाओं AB और QR के बीच स्थित हैं।∴
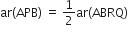...(i)इस प्रकार ar (PCD) =
...(ii) (i) और (ii) से
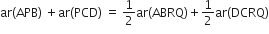
अत:
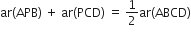
(ii) इसी प्रकार
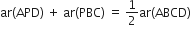
अत:
