दर्शाइए कि समान्तर चतुर्भुज के दोनों विकर्ण उसे बराबर क्षेत्रफलों वाले चार त्रिभुजों में बाटँते हैं।

ज्ञात है: चतुर्भुज ABCD के विकर्ण AC और BD बिंदु O पर प्रतिच्छेद करते हैं। इस प्रकार चार त्रिभुजें AOD, AOB, COB और COD बनते हैं।
सिद्ध करना हैं: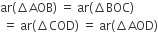


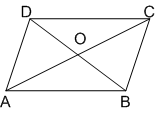
प्रमाण: चूँकि एक ||gm के विकर्ण परस्पर समद्विभाजित करते हैं।
∴  O, मध्यबिंदु है (AC और BD का)
अब, ΔABC में OB एक माध्यिका है।
∴   ar(ΔAOB) = ar(ΔBOC)       ...(i)
                       [∵ माध्यिका Δ को दो समान क्षेत्रफलों वाली Δ में बांटती  हैं]
इसी प्रकार, 
    ar(ΔBOC) = ar(ΔCOD)         ...(ii)
और ar(ΔCOD) = ar(ΔAOD)        ...(iii)
(i), (ii) और (iii) से,
ar(ΔAOB) = ar(ΔBOC)
             = ar(ΔCOD)
             = ar(ΔAOD)