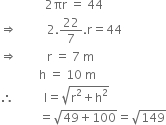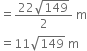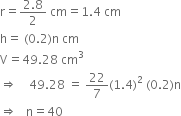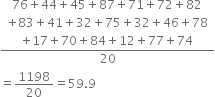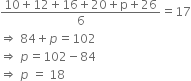Mathematics Chapter 15 Probability
Sponsor Area
NCERT Solution For Class 9 About 2.html
A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine:
(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costsर 20.
(i) l = 1.5 m
b= 1.25 m
h = 65 cm = 0.65 m.
∴ The area of the sheet required for making the box = lb + 2(bh + hl)
= (1.5)(1.25) + 2 {(1.25)(0.65) + (0.65)(1.5)} = 1.875 + 2{0.8125 + 0.975}
= 1.875 + 2(1.7875) = 1.875 + 3.575 = 5.45 m2.
(ii) The cost of sheet for it = र 5.45 x 20 = र 109.
The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of र 7.50 per m2.
l = 5 m
b = 4 m
h = 3 m
Area of the walls of the room = 2(l + b) h
= 2(5 + 4) 3 = 54 m2
Area of the ceiling = lb
= (5) (4) = 20 m2
∴ Total area of the walls of the room and the ceiling = 54 m2 + 20 m2 = 74 m2
∴ Cost of white washing the walls of the room and the ceiling = 74 x 7.50 = र 555.
The floor of a rectangular hall has a perimeter 250 m. If the cost of painting the four walls at the rate of ` 10 per m2 is ` 15000, find the height of the hall. [Hint : Area of the four walls = Lateral surface area.]
Let the length, breadth and height of the rectangular hall be l m, b m and h m respectively.
Perimeter = 250 m
⇒ 2(l + b) = 250
⇒ l + b = 125 ...(1)
Area of the four walls
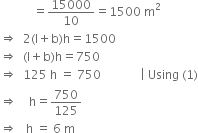
Hence, the height of the hall is 6 m.
The paint in a certain container is sufficient to paint an area equal to 9.375 m2. How many bricks of dimensions 22.5 cm × 10 cm × 7.5 cm can be painted out of this container?
For a brick
l = 22.5 cm b = 10 cm h = 7.5 cm
∴ Total surface area of a brick = 2 (lb + bh + hl)
= 2(22.5 x 10 + 10 x 7.5 + 7.5 x 22.5)
= 2(225 + 75 + 168.75)
= 2(468.75) = 937.5 cm2 = .09375 m2
∴ Number of bricks that can be painted out![]()
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
Each edge of the cubical box (a) = 10 cm
∴ Lateral surface area of the cubical box = 4a2 = 4(10)2 = 400 cm2.
For cuboidal box
l = 12.5 cm b = 10 cm h = 8 cm
Lateral surface area of the cuboidal box = 2(l + b) h
= 2(12.5+ 10)(8) = 360 cm2.
∴ Cubical box has the greater lateral surface area than the cuboidal box by (400 – 360) cm2, i.e., 40 cm2.
A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.
(i) Which box has the greater lateral surface area and by how much?
Total surface area of the cubical box = 6a2
= 6(10)2 = 600 cm2
Total surface area of the cuboidal box
= 2 (lb + bh + hl)
= 2[(12.5)(10) + (10)(8) + (8)(12.5)]
= 2[125 + 80 + 100] = 610 cm2.
Cubical box has the smaller total surface area than the cuboidal box by (610 – 600) cm2, i.e., 10 cm2.
A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.
(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?
(i) For herbarium
l = 30 cm b = 25 cm h = 25 cm
Area of the glass = 2(lb + bh + hl)
= 2[(30)(25) + (25)(25) + (25)(30)] = 2[750 + 625 + 750] = 4250 cm2.
(ii) The tape needed for all the 12 edges = 4 (l + b + h)
= 4(30 + 25 + 25) = 320 cm.
Shanti Sweets Stall was placing an order for making cardboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25 cm x 20 cm x 5 cm and the smaller of dimensions 15 cm x 12 cm x 5 cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the cardboard is र 4 for 1000 cm2, find the cost of cardboard required for supplying 250 boxes of each kind.
For bigger box
l = 25 cm b = 20 cm h = 5 cm
Total surface area of the bigger box
= 2 (lb + bh + hl)
= 2[(25)(20) + (20)(5) + (5)(25)]
= 2[500 + 100 + 125] = 1450 cm2
Cardboard required for all the overlap![]()
∴ Net surface area of the bigger box
= 1450 cm2 + 72.5 cm2 = 1522.5 cm2
∴ Net surface area of 250 bigger boxes
= 1522.5 x 250 = 380625 cm2
Cost of cardboard
![]()
For smaller box
l = 15 cm b = 12 cm h = 5 cm
∴ Total surface area of the smaller box = 2 (lb + bh + hl)
= 2[(15)(12) + (12)(5) + (5)( 15)] = 2[ 180 + 60 + 75] = 630 cm2
Cardboard required for all the overlaps![]()
∴ Net surface area of the smaller box
= 630 cm2 + 31.5 cm2 = 661.5 cm2 Net surface area of 250 smaller boxes = 661.5 x250 = 165375 cm2
∴ Cost of cardboard![]()
Cost of cardboard required for supplying 250 boxes of each kind
= र 1522.50 + र 661.50 = र 2184.
Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m × 3 m?
For shelter
l = 4 m b = 3 m h = 2.5m
∴ Total surface area of the shelter = lb + 2 (bh + hl)
= (4)(3) + 2[(3)(2.5) + (2.5) (4)] = 12 + 2[7.5 + 10] = 47 m2 Hence, 47 m2 of tarpaulin will be required.
The length of a hall is 20 m and width 16 m. The sum of the areas of the floor and the flat roof is equal to the sum of the areas of the four walls. Find the height of the hall.
Let the height of the hall be h m.
Area of the floor = l x b
= 20 x 16 = 320 m2 Area of the flat roof = l x b
= 20 x 16 = 320 m2 Sum of the areas of the four walls = 2(l + b) h
= 2(20 + 16) h = 72 h m2 According to the question,
72 h = 320 + 320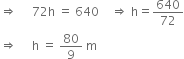
Hence, the height of the hall is ![]()
A closed iron tank 12 m long, 9 m wide and 4 m deep is to be made. Determine the cost of iron sheet used at the rate of र 50 per metre, the sheet being 2 m wide.
For tank
I = 12 m b = 9 m h = 4 m Total surface area of the tank
= 2 (I x b + b x h + h x l)
= 2(12 x 9 + 9 x 4 + 4 x 12),
= 2(108 + 36 + 48)
= 2(192) = 384 m2 Width of the iron sheet = 2 m
∴ Length of the iron sheet = ![]()
Cost of the iron sheet = 192 x 50 = र 9600.
A table cover 4 m x 2 m is spread on a table. Find the cost of polishing the top of the table at र40 per square metre of 25 cm table cover is hanging all round the table.
For table cover
l = 4 – (0.25 + 0.25)
| ∵ 25 cm = 0.25 m
= 3.5 m b = 2 – (0.25 + 0.25) = 1.5 m
∴ Area of the cover = l x b
= 3.5 x 1.5 = 5.25 m2 Cost of polishing the top of the table at र 40 per square metre = 5.25 x 40 = र 210.
The cost of papering the four walls of a room at 70 paise per square metre is र 157.50. The height of the room is 5 metres. Find the length and the breadth of the room if they are in the ratio 4 : 1.
Let the length and the breadth of the room be 4x m and x m respectively.
Area of the four walls of the room = 2(l + b) h
= 2(4x + x) 5 = 50 x m2
Cost of papering the four walls of the room @ 70 paise per square metre
= र 50x x 0.70 = र 35x According to the question,
35x = 157.50![]()
∴ Breadth of the room = 4.5 m
∴ Length of the room = 4 x 4.5 m = 18 m.
A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.4 m and three windows each measuring 2 m x 1 m. The interior wall is to be colour washed. Find the cost of colour washing at the rate of र 3.50 per m2.
For classroom
l = 1 m b = 6.5 m h = 4 m Area to be colour washed
= 2(l + b) h – [3 x 1.4 + 3 {2 x 1}] = 2(7 + 6.5) 4 – (4.2 + 6)
= 108 – 10.2 = 97.8 m2
Cost of colour washing = 97.8 x 3.50 = र 34.30
Two cubes of side 6 cm each, are joined end to end. Find the surface area of the resulting cuboid.
For resulting cuboid Length (l) = 6 + 6 = 12 cm Breadth (b) = 6 cm Height (h) = 6 cm
∴ Surface area
= 2 (lb + bh + hl)
= 2(12 x6 + 6x6 + 6x 12)
= 360 cm2
The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of र 8 and र 9.50 per m2 is र1248. Find the dimensions of the box.
Let the dimensions of the box be 2k, 3k and 4k.
Total surface area = 2(lb + bh + hl)
= 2(2k ⋅ 3k + 3k ⋅ 4k + 4k ⋅ 2k)
= 52k2 m2
Cost of covering at the rate of र 8 per m2 = 52k2 x 8 = र416 k2
Cost of covering at the rate of र 9.50 per m2 = 52k2 x 9.50 = र 494k2
Difference between the costs = र 494k2 – र 416k2 = र 78k2
According to the question,
78k2 = 1248 ⇒ k2 = 16 ⇒ k = 4 Hence, the dimensions of the box are 8 m, 12 m and 16 m.
The length, breadth and height of a cuboid are 15 cm, 10 cm and 20 cm. Find the surface area of the cuboid.
Solution not provided.
Ans. 1300 cm2
Sponsor Area
Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden block covered with coloured paper with picture of Santa Claus on it (see figure). She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80 cm, 40 cm and 20 cm respectively how many square sheets of paper of side 40 cm would she require?

Solution not provided.
Ans. 11200 cm2
Hameed has built a cubical water tank with lid for his house, with each outer edge 1.5 m long. He gets the outer surface of the tank excluding the base, covered with square tiles of side 25 cm (see figure). Find how much he would spend for the tiles, if the cost of the tiles is र 360 per dozen.
Solution not provided.
Ans. र 5400
Three cubes each of the side 3 cm are joined end to end. Find the surface area of the resulting cuboid.
Solution not provided.
Ans. 126 cm2
The dimensions of a rectangular box are in the ratio 2 : 3 : 4 and difference between the cost of covering it with sheet of paper at the rate of र 4 and र 4.50 per m2 is र 416. Find the dimensions of the box.
Solution not provided.
Ans. 8 m, 12 m, 16 m
The edge of a cube is 10.5 mm. Find its total surface area in cm2.
Solution not provided.
Ans. 6.615 cm2
If the length of the diagonal of a cube is 6√3 cm, find the edge of the cube.
Solution not provided.
Ans. 6 cm
Three cubes are placed adjacent to each other in a row. Find the ratio of the total surface area of the cuboid so formed and that of any one of these cubes.
Solution not provided.
Ans. 10 : 3
The surface area of a cuboid is 1372 cm2. If its dimensions are in the ratio 4 : 2 : 1, find its length.
Solution not provided.
Ans. 28 cm
The curved surface area of a right circular cylinder of height 14 cm is 88 cm2 . Find the diameter of the base of the cylinder.
h = 14 cm
Curved surface area = 88 cm2 | Given
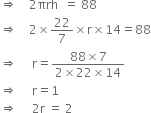
Hence, the diameter of the base of the cylinder is 2 cm.
It is required to make a closed cylindrical tank of height 1 m and base diameter 140 cm from a metal sheet. How many square metres of the sheet are required for the same?
h = 1 m = 100 cm
2r = 140 cm![]()
Total surface area of the closed cylindrical tank = 2πr(h + r)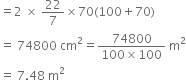
Hence, 7.48 square metres of the sheet are required.
A metal pipe is 77 cm long. The inner diameter of a cross section is 4 cm, the outer diameter being 4.4 cm. Find its
(i) inner curved surface area,
(ii) outer curved surface area,
(iii) total surface area.
h = 77 cm
2r = 4 cm
⇒ r = 2 cm
2R = 4.4 cm
⇒ R = 2.2 cm
(ii) Outer curved surface area =
(iii) Total surface area
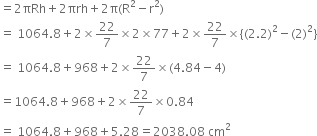
The diameter of a roller is 84 cm and its length is 120 cm. It takes 500 complete revolutions to move once over to level a playground. Find the area of the playground in m2.
2 r = 84 cm
⇒ r = 42 cm
h = 120 cm
∴ Area of the playground levelled in taking 1 complete revolution
![]()
![]() Area of the playground = 31680 x 500
Area of the playground = 31680 x 500
![]()
Hence, the area of the playground is 1584 m2.
A cylindrical pillar is 50 cm in diameter and 3.5 m in height. Find the cost of painting the curved surface of the pillar at the rate of र 12.50 per m2.
2r = 50 cm
∴ r = 25 cm = 0.25 m h = 3.5 m
∴ Curved surface area of the pillar = 2πrh![]()
Cost of painting the curved surface of the pillar at the rate of र 12.50 per m2
= र 5.5 x 12.50 = र 68.75.
Curved surface area of a right circular cylinder is 4.4 m2. If the radius of the base of the cylinder is 0.7 m, find its height.
r = 0.7 m
Curved surface area = 4.4 m2
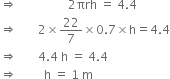
Hence, the height of the right circular cylinder is 1 m.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find
(i) its inner curved surface area,
(ii) the cost of plastering this curved surface at the rate of र 40 per m2.
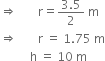
∴ Inner curved surface area of the circular well = 2πrh
(ii) Cost of plastering the curved surface at the rate of र 40 per m2
= र 110 x 40 = र 4400.
In a hot water heating system, there is a cylindrical pipe of length 28 m and diameter 5 cm. Find the total radiating surface in the system.
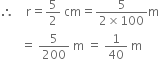
Total radiating surface in the system = 2πrh
Find:
(i) the lateral or curved surface area of a closed cylindrical petrol storage tank that is 4.2 m in diameter and 4.5 m high.
(i) 2r = 4.2 m![]()
h = 4.5 m
Lateral or curved surface area = 2πrh
![]()
Find:
(ii) how much steel was actually used if of the steel actually used was wasted in making the tank?
(ii) Total surface area = ![]()
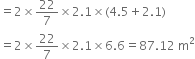
Let the actual area of steel used be x m2.
Since 1/12 of the actual steel used was wasted, the area of the steel which has gone into the tank = 11/12 of x.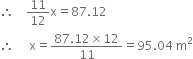
![]() Steel actually used = 95.04 m2
Steel actually used = 95.04 m2
In Fig. 13.12, you see the frame of a lampshade. It is to be covered with a decorative cloth. The frame has a base diameter of 20 cm and height of 30 cm. A margin of 2.5 cm is to be given for folding it over the top and bottom of the frame. Find how much cloth is required for covering the lampshade.
2r = 20 cm ⇒ r = 10 cm h = 30 cm
Cloth required = 2πr(h + 2.5 + 2.5)![]()
= 2200 cm2.
The students of a Vidyalaya were asked to participate in a competition for making and decorating penholders in the shape of a cylinder with a base, using cardboard. Each penholder was to be of radius 3 cm and height 10.5 cm. The Vidyalaya was to supply the competitors with cardboard. If there were 35 competitors, how much cardboard was required to be bought for the competition?
r = 3 cm
h = 10.5 cm
∴ Cardboard required for 1 competitor![]()
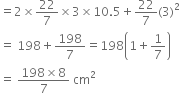
∴ Cardboard required for 35 competitors![]()
Hence, 7920 cm2 of cardboard was required to be bought for the competition.
Sponsor Area
A cast-iron pipe has an external diameter of 75 mm. If it is 4.2 m long, find the area of the outer surface.

Length of the pipe (h)
= 4.2 m = 4.2 x 100 cm = 420 cm Area of the outer surface = 2πrh![]()
A cylindrical vessel, without lid, has to be tin-coated including both of its sides. If the radius of its base is 1/2 m and its height is 1.4 m, calculate the cost of tin-coating at the rate of र 50 per 100 cm2. (Use  = 3.14)
= 3.14)
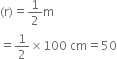
Height (h) = 1.4 m
= 1.4 x 100 cm = 140 cm
Surface area to be tin-coated = 2(2πrh + πr2)
= 2[2 x 3.14 x 50 x 140 + 3.14 x (50)2]
= 2 [43960 + 7850] = 2(51810)
= 103620 cm2
∴ Cost of tin-coating at the rate of र 50 per 1000 cm2![]()
10 cylindrical pillars of a building have to be painted. If the diameter of each pillar is 50 cm and the height 4 m, what will be the cost of painting at the rate of र 14 per square metre?
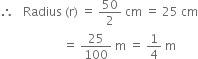
Height (h) = 4 m
∴ Curved surface area of 1 pillar = 2![]() rh
rh
Curved surface area of 10 pillars
∴ Cost of painting at the rate of र 14 per square metre =
A cylinder 3 m high, is open at the top. The circumference of its base is 22 cm. Find its total surface area.
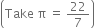
Let the base radius of the cylinder be r cm.
Then,
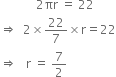
h = 3 m![]() Toatal surface area =
Toatal surface area = ![]()
![]()
= 66 + 38.5
= 104.5 m2
Twenty cylindrical pillars of a building are to be cleaned. If the diameter of a pillar is 0.5 m and height is 4 m, what will be the cost of cleaning them at the rate of र 3 per m2. (Take  = 3.14)
= 3.14)
Radius (r) =
Height (h) = 4 m
∴ Curved surface area = 2πrh
= 2 x 3.14 x 0.25 x 4 = 6.28 m2
∴ Curved surface area of 20 pillars
= 6.28 x 20 m2 = 125.6 m2
∴ Cost of cleaning them
= 125.6 x 3 = र 376.80
Find the curved surface area of a closed cylindrical petrol storage tank that is 3.8 m in diameter and 4.9 m high.
h = 4.9 m
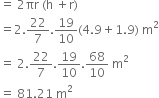
The diameter of roller 1.5 m long is 84 cm. If it takes 100 revolutions to level a playground, find the cost of levelling this ground at the rate of 50 paise per square metre.
h = 84 cm = 0.84 m
∴ Area of the ground levelled in 1 revolution = 3.96 m2
∴ Area of the ground levelled in 100 revolutions
= 3.96 x 100 m2 = 396 m2
∴ Cost of levelling
The cost of painting the total outside surface of a closed cylindrical tank at 60 paise per sq. d.m. is र 237.60. The height of the tank is 6 times the radius of the base of the tank. Find its volume correct to two decimal places.
= 396 dm2
Let the radius of the base of the tank be r dm. Then, height = 6 r dm
∴ Curved surface area = 2πRH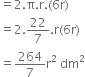
According to the question,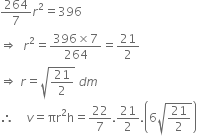
= 198 x 3.24 = 641.52 dm3
Savitri had to make a model of a cylindrical kaleidoscope for her science project. She went to buy the chart paper to make the curved surface of the kaleidoscope. What would be the area of chart paper required by her, if she wanted to make a kaleidoscope of length 25 cm with a 3.5 cm radius? You may take 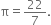
Solution not provided.
Ans. 550 cm2
The radii of two right circular cylinders are in the ratio 2 : 3 and their heights are in the ratio 5 : 4. Calculate the ratio of their curved surface areas.
Solution not provided.
Ans. 5 : 6
A cylindrical tower is 5 m in diameter and 14 m high. Find the cost of white-washing its curved surface at र 10 per square metre.
Solution not provided.
Ans. र 2200
The height of a right circular cylinder is 15 cm. Its curved surface area is 660 cm2. Find the radius of its base.
Solution not provided.
Ans. 7 cm
A right circular cylinder is 3 m high and the circumference of its base is 22 m. Find its curved surface area.
Solution not provided.
Ans. 66 m2
The diameter of a circular wall is 4.5 m and its depth is 14 m. Find the cost of cementing the in ner surface of the wall at र 120 per sq. m.
Solution not provided.
Ans. र 23760
A metal pipe is 77 cm long. The inner diameter of a cross-section is 4 cm and outer diameter is 5.0 cm. Find its
(i) Inner curved surface area
(ii) Outer curved surface area
Solution not provided.
Ans. (i) 968 cm2 (ii) 1210 cm2
A cylinder 6 m high, is open at the top. The circumference of its base is 22 m. Find its total surface area.
Solution not provided.
Ans. 209 m2
A solid cylinder has a total surface area 462 cm2. Its curved surface area is one-third of the total surface area. Find the height of the cylinder.
Solution not provided.
Ans. 3.5 cm
A heap of rice is in the form of a cone whose diameter is 48 m and height 10 m. The heap is to be covered by canvas to protect it from rain. Find the cost of canvas required at र 70/m2.
Solution not provided.
Ans. र 137155.20
Diameter of the base of a cone is 10.5 cm and its slant height is 10 cm. Find its curved surface area.
= 5.25 cm Slant height (l) = 10 cm
∴ Curved surface area of the cone = πrl
Find the total surface area of a cone, if its slant height is 21 m and diameter of its base is 24 m.
∴ Total curved surface area of the cone = πr(l + r)

Curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find (i) radius of the base and (ii) total surface area of the cone.
(i) Slant height (l) = 14 cm Curved surface area = 308 cm2
⇒ πrl = 308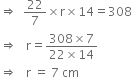
Hence, the radius of the base is 7 cm.
(ii) Total surface area of the cone = πr(l + r)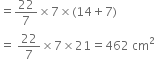
Hence, the total surface area of the cone is 462 cm2.
A conical tent is 10 m high and the radius of its base is 24 m. Find:
(i) slant height of the tent.
(ii) cost of the canvas required to make the tent, if the cost of 1 m2 canvas is र 70.
= 26 m
Hence, the slant height of the tent is 26 m.
(ii) Curved surface area of the tent = ![]() rl
rl![]()
Cost of the canvas required to make the tent, if the cost of 1 m2 canvas is र 70.![]()
= र 137280.
Hence, the cost of the canvas is र 137280.
What length of tarpaulin 3 m wide will be required to make conical tent of height 8 m and base radius 6m? Assume that the extra length of material that will be required for stitching margins and wastage in cutting is approximately 20 cm (Use  = 3.14)
= 3.14)
For conical tent
h = 8 m r = 6 m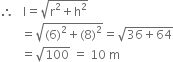
∴ Curved surface area = πrl
= 3.14 x 6 x 10 = 188.4 m2. Width of tarpaulin = 3 m![]() Length of tarpaulin =
Length of tarpaulin = ![]()
Extra length of the material required = 20 cm = 0.2 m
∴ Actual length of tarpaulin required = 62.8 m + 0.2 m = 63 m.
The slant height and base diameter of a conical tomb are 25 m and 14 m respectively. Find the cost of white-washing its curved surface at the rate of र 210 per 100 m2.
∴ Curved surface area of the tomb =
Cost of white-washing the curved surface of the tomb at the rate of र 210 per 100 m2
7.A joker’s cap. is in the form of a right circular cone of base radius 7 cm and height 24 cm. Find the area of the sheet required to make 10 such caps.
Base radius (r) = 7 cm
Height (h) = 24 cm![]() Slant height (l) =
Slant height (l) = ![]()
![]()
![]() Curved surface area of a cap =
Curved surface area of a cap = ![]()
![]()
∴ Curved surface area of 10 caps = 550 x 10 = 5500 cm2
Hence, the area of the sheet required to make 10 such caps is 5500 cm2.
A bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is. र 12 per m2, what will be the cost of painting all these cones? (Use  = 3.14 and take
= 3.14 and take 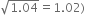
Base diameter = 40 cm![]() Base radius (r) =
Base radius (r) = ![]() cm = 20 cm
cm = 20 cm
= ![]()
Height (h) = 1 m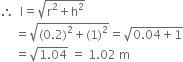
Curved surface area = πrl
= 3.14 x 0.2 x 1.02 = 0.64056 m2
∴ Curved surface area of 50 cones = 0.64056 x 50 m2 = 32.028 m2
∴ Cost of painting all these cones = 32.028 x 12
= 384.336 = र 384.34 (approximately).
The curved surface area of a right circular cone is 12320 cm2. If the radius of its base is 56 cm, find its height.
Let the height of the right circular cone be h cm. r = 56 cm Curved surface area = 12320 cm2 ⇒ πrl = 12320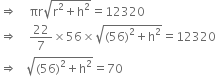
⇒ (56)2 + h2 = (70)2
| Squaring both sides
⇒ h2 = (70)2 – (56)2
⇒ h2 = (70 – 56)(70 + 56)
⇒ h2 = (14)(126)
⇒ h2= (14)(14 x 9)
⇒ h = 14 x 3 = 42
| Extracting square root
Hence, the height of the right circular cone is 42 cm.
Find the total surface area of a cone whose radius is and slant height is 2l.
Total surface area
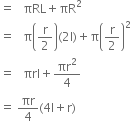
CSA of an ice cream cone of slant height 12 cm is 113.04 cm2. Find the base radius and height of the cone, ( = 3.14)
= 3.14)
Let the base radius and height of the cone be r cm and h cm respectively. Then,
πrl = 113.04 ⇒ 3.14 x r x 12 = 113.04 ⇒ r = 3 cm
l2 = r2 + h2 ⇒ (12)2 = (3)2 + h2
⇒ 144 = 9 + h2
⇒ h2 = 135![]()
The radius and vertical height of a cone are 5 cm and 12 cm respectively. Find the curved surface area.
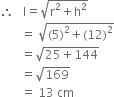
∴ Curved surface area = πrl = π(5)(13) = 65π cm2
Find the area of the metal sheet required to make two closed hollow cones each of height 24 cm and slant height 25 cm.
h = 24 cm l = 25 cm
l2 = r2 + h2
⇒ (25)2 = r2 + (24)2 ⇒ r = 7 cm
∴ Area of the metal sheet required = 2(![]() rl)
rl)![]()
= 600 cm2
A cylindrical tent has a conical top with dimension as shown in the figure. Calculate the total cost of the canvas required to make the tent, if the cost of canvas is र 50 per sq. m.
For cone
Base radius (r) = 8 m
Height (h) = 6m![]()
= 10 m
∴ Curved surface area = πrl = π(8)(10) = 80π m2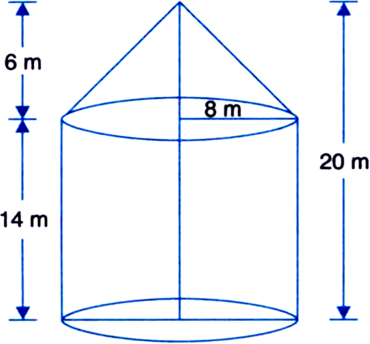
For cylinder
Base radius (R) = 8 m Height (H) = 14 m
∴ Curved surface area = 2πRH = 2 ⋅ π ⋅ 8 ⋅ 14 = 224π m2 Total curved surface area = Curved surface area of the cone + Curved surface area of the cylinder
= 80π + 224π = 304π m2 = 304 x 3.14 m2 = 954.56 m2
∴ Cost of canvas = 954.56 x 50 = र 47728
Find the curved surface area of a right circular cone, whose slant height is 10 cm and base radius is 7 cm.
Solution not provided.
Ans. 220 cm2
The height of a cone is 16 cm and its base radius is 12 cm. Find the curved surface area and the total surface area of the cone. (Use  = 3.14)
= 3.14)
Solution not provided.
Ans. 753.6cm2, 1205.76cm2
The radius and height of a right circular cone are in the ratio 4 : 3. If the area of the base of the cone is 154 cm2, find the area of its curved sur-  .
.
Solution not provided.
Ans. 192.5 cm2
Sponsor Area
Find the total surface area of a solid cone if its slant height is 21 cm and diameter of its base is 24 cm.
Solution not provided.
Ans. ![]()
The radius and slant height of a cone are in the ratio 4 : 7. If its curved surface area is 792 cm2, find its height.
Solution not provided.
Ans. ![]()
The circumference of the base of a 24 m high solid wooden cone is 44 m. Find its curved surface area.
Solution not provided.
Ans. 550 m2
How many metres of cloth 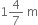 wide will be required to make a conical tent whose base diameter is 10 m and whose vertical height is 12 cm?
wide will be required to make a conical tent whose base diameter is 10 m and whose vertical height is 12 cm?
Solution not provided.
Ans. 130 m
What length of canvas 3 m wide will be required to make a conical tent of height 8 m and radius of base 6 m? (Use  = 3.14)
= 3.14)
Solution not provided.
Ans. 62.8 m
A circus tent is in the form of a cone of height 15 m and diameter 16 m. Find the length of the canvas needed to make the tent if the width of the canvas is 2 m. (Use  = 3.14)
= 3.14)
Solution not provided.
Ans. 213.52 m
What is the radius and curved surface of a cone made from a quadrant of a circle of radius 28 cm?
Solution not provided.
Ans. 7 cm, 616 cm2
Find the surface area of a sphere of radius:
(i) 10.5 cm (ii) 5.6 cm (iii) 14 cm.
= 1386 cm2.
(ii) r = 5.6 cm
∴ Surface area = 4πr2![]()
= 394.24 cm2.
(iii) r = 14 cm
Surface area = 4πr2![]()
Find the surface area of a sphere of diameter:
14 cm
∴ Surface area = 4πr2
Find the surface area of a sphere of diameter:
21 cm
∴ Surface area = 4πr2
= 1386 cm2.
Find the surface area of a sphere of diameter:
3.5 m.
Diameter = 3.5 m![]() Radius (r) =
Radius (r) = ![]()
![]() Surface area =
Surface area = ![]()
![]()
Find the total surface area of a hemisphere of radius 10 cm. (Use ![]() = 3.14)
= 3.14)
r = 10 cm.
∴ Total surface area of the hemisphere = 3πr2
= 3 x 3.14 x (10)2 = 942 cm2.
The radius of a spherical balloon increases from 7 cm to 14 cm as air is being pumped into it. Find the ratio of surface areas of the balloon in the two cases.
Case I. r = 7 cm
∴ Surface area = 4![]() r2
r2![]()
Case II. r = 14 cm
∴ Surface area = 4πr2![]()
= 2464 cm2
∴ Ratio of surface areas of the balloon = 616 : 2464![]()
A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ` 16 per 100 cm2.
Inner surface area = 2πr2
Cost of tin-plating at the rate of र 16 per 100 cm2
Find the radius of a sphere whose surface area is 154 cm2.
Surface area = 15.4 cm2
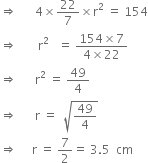
Hence, the radius of the sphere is 3.5 cm.
The diameter of the moon is approximately one fourth of the diameter of the earth. Find the ratio of their surface areas.
Then diameter of the moon =
and, Radius of the moon =
and, Surface area of the moon
Ratio of their surface areas =
A hemispherical bowl is made of steel, 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Inner radius of the bowl = 5 cm
Thickness of steel = 0.25 cm
∴ Outer radius of the bowl
= 5 + 0.25 = 5.25 cm
∴ Outer curved surface of the bowl = 4πr2![]()
= 346.5 cm2.
A right circular cylinder just encloses a sphere of radius r. Find
(i) surface area of the sphere,
(ii) curved surface area of the cylinder,
(iii) ratio of the areas obtained in (i) and (ii).
(i) Surface area of the sphere = 4πr2
(ii) For cylinder Radius of the base = r
Height = 2 r Curved surface area of the cylinder = 2π(r)(2r) = 4πr2
(iii) Ratio of the areas obtained in (i) and (ii)![]()
If the radius of a sphere is halved then what is the decrease in its surface area?
Let the radius of the sphere be r.
Then surface area of the sphere = 4πr2
New radius of the sphere = ![]()
![]() New surface area of the sphere
New surface area of the sphere ![]()
![]() Decrease in surface area =
Decrease in surface area = ![]()
![]()
= ![]() ( surface area of the original sphere).
( surface area of the original sphere).
The surface area of a sphere of radius 5 cm is 5 times the area of the curved surface of a cone of radius 4 cm. Find the height of the cone.
Surface area of sphere of radius 5 cm = 4π (5)2 cm2
Area of the curved surface of cone of radius 4 cm = π(4) l cm2 where I cm is the slant height of the cone.
According to the question,
4![]() (5)2 = 5[
(5)2 = 5[![]() (4)l}
(4)l}![]() l = 5 cm
l = 5 cm![]()
![]() r2 + h2 = 25
r2 + h2 = 25 ![]() (4)2 + h2 = 25
(4)2 + h2 = 25![]() 16 + h2 + 25
16 + h2 + 25 ![]() h2 = 9
h2 = 9![]() h = 3
h = 3
Hence, the height of the cone is 3 cm.
The external and internal diameters of a hollow hemispherical vessel are 16 cm and 12 cm respectively. The cost of painting 1 sq. cm of surface is र 2. Find the cost of painting the vessel all over.
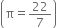
External radius of (R) = ![]()
Internal radius (r) = ![]()
∴ Total surface area
= 2πR2 + 2πr2 + π(R2 – r2)
= 27π(8)2 + 2π(6)2 + π(82 – 62) = 128π + 72π + 28π = 228π![]()
= र 1433.14
A hemispherical bowl made of steel is of 1 cm thickness. The inner radius of the bowl is 6 cm. Find the total surface area of the bowl, in terms of π.
Inner Radius (r) = 6 cm
Outer Radius (R) = 6 cm + 1 cm = 7 cm
Total surface area of the bowl
= 2πr2 + 2πR2 + π(R2 – r2)
= 2π(6)2 + 2π(7)2 + π(72 – 62)
= 72π + 98π+ 13π
= 183π cm2
Find the surface area of a sphere of radius 7 cm.
Solution not provided.
Ans. (i) 2772 cm2 (ii) 4158 cm2
The hollow sphere, in which the circus motorcyclist performs his stunts, has a diameter of 7 m. Find the area available to the motorcyclist for riding.
Solution not provided.
Ans. 154 m2
The internal and external diameters of a hollow hemispherical vessel are 24 cm and 25 cm respectively. The cost to paint 1 sq. cm of surface is र 1.75. Find the total cost to the nearest rupee to paint the vessel all over. Ignore the area of the edge. (Take ![]() = 3.14)
= 3.14)
Solution not provided.
Ans. र 269
A hemispherical dome is to be painted from the inside. The circumference of the dome is 176 m. Find the area to be painted.
Solution not provided.
The diameter of a sphere is decreased by 25%. By what percent will its curved surface area be decreased?
Solution not provided.
Ans. ![]()
The total surface area of a solid hemisphere is 5940 cm2. Find the diameter of the hemisphere.
Solution not provided.
Ans. 50.18 cm
A matchbox measures 4 cm × 2.5 cm × 1.5 cm. What will be the volume of a packet containing 12 such boxes?
Volume of a matchbox = 4 x 2.5 x 1.5 cm3 = 15 cm3
∴ Volume of a packet containing 12 such boxes = 15 x 12 cm3 = 180 cm3.
A cuboidal water tank is 6 m long, 5 m wide and 4.5 m deep. How many litres of water can it hold? (1 m3 = 1000 l)
Capacity of the tank = 6 x 5 x 4.5 m3 = 135 m3
∴ Volume of water it can hold = 135 m3 = 135 x 1000 l = 135000 l.
A cuboidal vessel is 10 m long and 8 m wide. How high must it be made to hold 380 cubic metres of a liquid?
Let the height of the cuboidal vessel be h m. l = 10 m b = 8 m
Capacity of the cuboidal vessel = 380 m3![]() lbh = 380
lbh = 380![]() (10)(8)h = 380
(10)(8)h = 380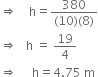
Hence, the cuboidal vessel must be made 4.75 m high.
Find the cost of digging a cuboidal pit 8 m long, 6 m broad and 3 m deep at the rate of र 30 per m3.
l = 8 m
b = 6 m h = 3 m
Volume of the cuboidal pit = Ibh = 8 x 6 x 3 m3 = 144 m3 Cost of digging the cuboidal pit @ र 30 per m3 = र 144 x 30
= र 4320.
The capacity of a cuboidal tank is 50000 litres of water. Find the breadth of the tank, if its length and depth are respectively 2.5 m and 10 m.
Let the breadth of the cuboidal tank be b m. l = 2.5 m h = 10 m
Capacity of the cuboidal tank = 50000 litres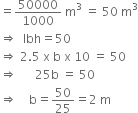
Hence, the breadth of the cuboidal tank is 2 m.
A village, having a population of 4000, requires 150 litres of water per head per day. It has a tank measuring 20 m × 15 m × 6 m. For how many days will the water of this tank last?
Requirement of water per head per day = 150 litres
∴ Requirement of water for the total population of the village per day
= 150 x 4000 litres![]()
= 600 m3
For tank
l = 20 m b = 15 m h = 6 m Capacity of the tank
= 20 x 15 x 6 m3 = 1800 m3
∴ Number of days for which the water of this tank last
= 600 m3
For tank
l = 20 m b = 15 m h = 6 m Capacity of the tank
= 20 x 15 x 6 m3 = 1800 m3
∴ Number of days for which the water of this tank last
A godown measures 40 m x 25 m x 10 m. Find the maximum number of wooden crates each measuring 1.5 m x 1.25 m x 0.5 m that can be stored in the godown.
For godown
l = 40 m b = 25 m h = 10 m
∴ Capacity of the godown = Ibh
= 40 x 25 x 10 m3 = 10000 m3
For a wooden crate
l = 1.5 m b = 1.25 m h = 0.5 m
∴ Capacity of a wooden crate = Ibh
= 1.5 x 1.25 x 0.5 m3 = 0.9375 m3
We have,![]()
Hence, the maximum number of wooden crates that can be stored in the godown is 10666.
Sponsor Area
A solid cube of side 12 cm is cut into eight cubes of equal volume. What will be the side of the new cube? Also, find the ratio between their surface areas.
Side of the solid cube (a) = 12 cm
∴ Volume of the solid cube = a3
= (12)3 = 12 x 12 x 12 cm3 = 1728 cm
∵ It is cut into eight cubes of equal volume.
∴ Volume of a new cube![]()
Let the side of the new cube be x cm.
Then, volume of the new cube = x3 cm3. According to the question, x3 = 216
∴ x = (216)1/3
∴ x = (6 x 6 x 6)1/3
∴ x = 6 cm
Hence, the side of the new cube will be 6 cm. Surface area of the original cube = 6a2 = 6(12)2 cm2 Surface area of the new cube
= 6x2 = 6(6)2 cm2
∴ Ratio between their surface areas![]()
Hence, the ratio between their surface areas is 4: 1.
A river 3 m deep and 40 m wide is flowing at the rate of 2 km per hour. How much water will fall into the sea in a minute?
In one hour
l = 2 km = 2 x 1000 m = 2000 m b = 40 m h = 3 m
∴ Water fell into the sea in one hour = Ibh = 2000 x 40 x 3 m3
∴ Water fell into the sea in a minute![]()
= 4000 m3
Hence, 4000 m3 of water will fall into the sea in a minute.
An underground water tank is in the form of a cuboid of edges 48 m, 36 m and 28 m. Find the volume of the tank.
For water tank l = 48 m b = 36 m h = 28 m
∴ Volume of the tank = Ibh
= 48 x 36 x 28 m3 = 48384 m3.
The areas of three adjacent faces of a cuboid are p, q and r. If its volume is v, prove that v2 = pqr.
Let the length, breadth and height of the cuboid be l, b and h units respectively. Then, p = lb q = bh r = hl
∴ pqr = (lb)(bh)(hl) = l2b2h2 ...(1) Again, v = Ibh
∴ v2 = (Ibh)2 = l2b2h2 ...(2)
(1) and (2) give
v2 = pqr.
Three cubes of edge 12 cm are joined together (end to end). Find the volume of the resulting cuboid.
For cuboid
Length (l) = 12 + 12 + 12 = 36 cm Breadth (b) = 12 cm Height (h) = 12 cm
∴ Volume of the resulting cuboid = Ibh
= 36 x 12 x 12 = 5184 cm3
A box with lid is made out of 2 cm thick wood. Its external length, breadth and height are 25 cm, 18 cm and 15 cm respectively. Find the capacity of the box and volume of the wood used.
Capacity of the box
= [25 – (2 + 2)} x [18 – (2 + 2)} x {15 – (2 + 2)} = 21 x 14 x 11 cm3 = 3234 cm3
Volume of the wood used
= 25 x 18 x 15 cm3 – 3234 cm3
= 6750 cm3 – 3234 cm3 = 3516 cm3
A rectangular metallic sheet has dimensions 48 cm x 36 cm. From each of its comers, a square of side 8 cm is cut off and an open box is made from the remaining sheet, find the volume of the box.
For open box
Length (l) = 48 – (8 + 8) = 32 cm Breadth (b) = 36 – (8 + 8) = 20 cm Height (h) = 8 cm
∴ Volume of the box = Ibh
= 32 x 20 x 8 = 5120 cm3
A cubical box has each edge of length 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high. Find the volume of the box which has greater lateral surface area.
Lateral surface area of cubical box = 4a2 = 4(10)2 = 400 cm2Lateral surface area of the cuboidal box = 2(l + b)h = 2(12.5 + 10)8 = 360 cm2
Clearly, the cubical box has greater lateral surface area.
∴ Volume of the cubical box = a3
= 103
= 1000 cm3
The total surface area of a cube isExample 3. The total surface area of a cube is 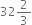 Find the volume of the cube.
Find the volume of the cube.
Let the length of each edge of the cube be a m.
Total surface area of the cube = ![]()
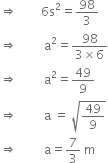
![]() Volumen of the cube = a3
Volumen of the cube = a3
![]() .
.
Find the length of the longest rod that can be placed in a room 12 m x 9 m x 8 m.
For room
l = 12m b = 9 m h = 8 m
Length of the longest rod that can be placed in the room
= Length of the diagonal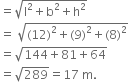
If v is the volume of a cuboid of dimensions a, b and c and s is its surface area, then prove that
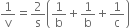
L. H. S. = ![]()
R. H. S. = ![]()
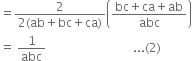
(1) and(2) given![]()
A cube and a cuboid have the same volume. The dimensions of the cuboid are in the ratio 1 : 2 : 4. If the difference between the cost of painting the cuboid and cube (whole surface area) at the rate of र 5/m2 is र 80, find their volumes.
Let the dimensions of the cuboid be ft m, 2k m, 4k m. Then,
Volume of the cuboid
= (k) (2k) (4k) m3 = 8k3 m3
Volume of the cube = 8k3 m3![]() Side of the cube =
Side of the cube = ![]()
Whole surface area of the cube = 6(2k)2 m2 = 24k2 m2 Page 240(2)
Whole surface area of the cuboid = 2 (lb + bh + hl)
= 2{k ⋅2k + 2k ⋅ 4k + 4k ⋅ k}
= 28k2 m2 Cost of painting the cube = (24k2) (5)
= र 120k2 Cost of painting the cuboid = (28k2) (5)
= र 140k2
Difference between the cost of painting the cuboid and cube
= र 140k2 – र 120k2 = र 20 k2 According to the question,
20k2 = 80 ⇒ k2 = 4 ⇒ k = 2
∴ Volume of the cube = 8k3 = 8(2)3 = 64 m3
= volume of the cuboid
A teak wood is cut first in the form of a cuboid of length 2.3 m, width 0.75 m and of a certain thickness. Its volume is 1.104 m3. How many rectangular planks of size 1.104 m3, how many rectangular planks of size 2.3 m x 0.75 m x 0.04 m can be cut from the cuboid?
Number of rectangular planks of size 2.3 m x 0.75 m x 0.04 m that can be cut from the cuboid
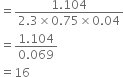
The length of a cinema hall is 20 m and its width is 16 m. The sum of the areas of its floor and flat roof is equal to the surface area of its four walls. Find the volume and height of the hall.
l = 20 m b = 16 m According to the question, 2 lb = 2(l + b)h
∴ lb = (I + b)h
∴ 20 x 16 = (20 + 16)h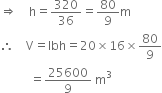
The length, breadth and height of a cuboid are 20 m, 24 m, 12 m respectively. The dimensions of length, breadth and depth are increased by 15%, 25% and 50% respectively. What is the ratio between the volume of the original cuboid and the new cuboid.
For original cuboid
Length (l) = 20 m Breadth (b) = 24 m Height (h) = 12 m Volume (V1) =lbh
= 20 x 24 x 12 m3 = 5760 m3
For new cuboid
Length (L) = 20m + 20 X ![]()
= 23 m
Breadth (B) = 24 m + 24 X ![]()
= 30 m
Height (H) = 12m + 12 X ![]()
= 18 m![]() Volume (V2) = LBH
Volume (V2) = LBH
= 23 x 30 x 18
= 12420 m3![]() Required ratio =
Required ratio = ![]()
![]()
![]() Volume of wall occupied by bricks
Volume of wall occupied by bricks
= 32.4 m3 - 3.24 m3
![]()
![]() Number of bricks
Number of bricks
![]()
Cost of bricks
![]()
= र 30375
A wall was to be built across an open ground to cover a width (or breadth) of 10 m. The height of the wall is 4 m and thickness of the wall is 24 cm. If this wall is to be built up with bricks whose dimensions are 24 cm x 12 cm x 8 cm, how many bricks would be required?
Solution not provided.
Ans. 4167 bricks
The length of the diagonal of a cube is  . What is the length of the edge of the cube?
. What is the length of the edge of the cube?
Solution not provided.
Ans. 2 cm
Volume of a rectangular block of stone is 2592 dm3 and its dimensions are in the ratio 4 : 3 : 1. Find its dimensions.
Solution not provided.
Ans. 24 dm, 18 dm, 6 dm2 cm
The length, breadth and height of a rectangular box are as 1 : 2 : 3. Find the volume of the box, when its surface area is 1078 sq. m.
Solution not provided.
Ans. 2058 m3
What is the volume of a cube whose total surface area is 864 nr?
Solution not provided.
Ans. 1728 m3
Three cubes each of volume 125 cm3 are joined end to end to form a cuboid. Find the total surface area of cuboid.
Solution not provided.
Ans. 350 cm2
A solid cube of side 16 cm is cut into eight cubes of equal volume. What will be the side of the new cube.
Solution not provided.
Ans. 8 cm
A solid cuboid of dimensions 12 cm x 18 cm x 10 cm is cut into cubes of side 2 cm. How many such cubes can be cut from the cuboid? Compare the total surface area of the cube and cuboid.
Solution not provided.
Ans. 270, 1 : 43
The lateral surface area of a cube is 324 cm2. Find its volume and the total surface area.
Solution not provided.
Ans. 729 cm3, 486 cm2
Find the volume, total surface area, lateral surface area and the length of diagonal of a cube, each of whose edges measures 20 cm.
Solution not provided.
Ans. 8000 cm3, 2400 cm2, 1600 cm2, ![]()
The height, breadth and length of a cuboidal box are in the ratio 1 : 2 : 3. Find the volume of the box if its surface area is 1078 dm2.
Solution not provided.
Ans. 2058 dm3
The length of a room is double its breadth. Its height is 3 m. The area of the four walls excluding a door of dimensions 4 m x 2 m is 100 m2. Find its volume.
Solution not provided.
Ans. 216 m3
The circumference of the base of a cylindrical vessel is 132 cm and its height is 25 cm. How many litres of water can it hold? (1000 cm3 = 1l)
Let the base radius of the cylindrical vessel be r cm.
Then, circumference of the base of the cylindrical vessel = 2πr cm.
According to the question,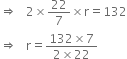
![]() r = 21 cm; h = 25 cm
r = 21 cm; h = 25 cm
∴ Capacity of the cylindrical vessel = ![]()
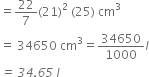
Hence, the cylindrical vessel can hold 34.65 l of water.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3of wood has a mass of 0.6 g.
∵ Outer diameter = 28 cm
∵ Outer radius (R) =
Length of the pipe (h) = 35 cm Outer volume =
Inner volume =
Volume of the wood used = Outer volume – Inner volume
= 21560 cm3 – 15840 cm3 = 5720 cm3
∴ Mass of the pipe = 5720 x 0.6 g
= 3432 g = 3.432 kg.
The inner diameter of a cylindrical wooden pipe is 24 cm and its outer diameter is 28 cm. The length of the pipe is 35 cm. Find the mass of the pipe, if 1 cm3 of wood has a mass of 0.6 g
(i) For tin can
l = 5 cm b = 4 cm h = 15 cm
∴ Capacity = l x b x h
= 5 x 4 x 15 cm3 = 300 cm3.
(ii) For plastic cylinder Diameter = 7 cm![]() Radius (r) =
Radius (r) = ![]()
Height (h) = 10 cm
∴ Capacity = ![]() r2h
r2h![]()
Clearly the second container i.e., a plastic cylinder has greater capacity than the first container i.e., a tin can by 385 – 300 = 85 cm3.
If the lateral surface of a cylinder is 94.2 cm2 and its height is 5 cm, then find (i) radius of its base (ii) its volume. (Use  = 3.14)
= 3.14)
h = 5 cm
Lateral surface = 94.2 cm2
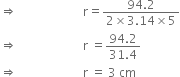
Hence, the radius of the base is 3 cm.
(ii) r = 3 cm h = 5 cm
∴ Volume of the cylinder = πr2h
= 3.14 x (3)2 x 5 = 141.3 cm3.
It costs र 2200 to paint the inner curved surface of a cylindrical vessel 10 m deep. If the cost of painting is at the rate of र 20 per m2, find
(i) inner curved surface area of the vessel,
(ii) radius of the base,
(iii) capacity of the vessel.
(i) Inner curved surface area of the vessel
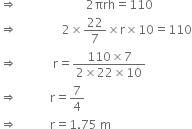
Hence, the radius of the base is 1.75 m.
(iii) r = 1.75 m
h = 10 m π Capacity of the vessel = ![]() r2h
r2h
Hence, the capacity of the vessel is 96.25 m3 (or 96.25 kl).
The capacity of a closed cylindrical vessel of height 1 m is 15.4 litres. How many square metres of metal sheet would be needed to make it?
Capacity = 15.4 litres =
= 0.0154 m3
Let the radius of the base be r m. Capacity = 0.0154 m3

∴ Curved surface area =
= 0.44+0.0308=0.4708 m2
Hence, 0.47 m2 of metal sheet should be needed.
A lead pencil consists of a cylinder of wood with a solid cylinder of graphite filled in the interior. The diameter of the pencil is 7 mm and the diameter of the graphite is 1 mm. If the length of the pencil is 14 cm, find the volume of the wood and that of the graphite.
For solid cylinder of graphite
Diameter = 1 mm![]() Radius (r) =
Radius (r) = ![]()
Length of the pencil (h) = 14 cm = 140 mm
∴ Volume of the graphite = ![]() r2h
r2h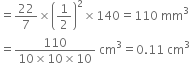
For cylinder of wood
Diameter = 7 mm![]() Radius (R) =
Radius (R) = ![]() mm
mm
Length of the pencil (h) = 14 cm = 140 mm![]() Volume of the wood
Volume of the wood 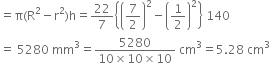
A patient in a hospital is given soup daily in a cylindrical bowl of diameter 7 cm. If the bowl is filled with soup to a height of 4 cm, how much soup the hospital has to prepare daily to serve 250 patients?
Height (h) = 4 cm
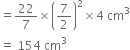
Volume of soup to be prepared daily to serve 250 patients
= 154 x 250 cm3 = 38500 cm3 (or 38.5l)
Hence, the hospital has to prepare 38500 cm3 (or 38.5l) of soup daily to serve 250 patients.
The volume of a cylinder is 448π cm3 and height 7 cm. Find its lateral surface area and total surface area.
Let the radius of the base of the cylinder be r cm.
h = 7 cm
Volume = 448![]() cm3
cm3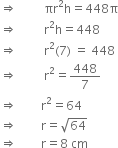
![]() Lateral surface area = 2
Lateral surface area = 2![]() rh
rh
![]()
Total surface area = ![]()
![]()
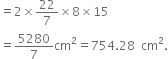
The diameter of the base of a right circular cylinder is 28 cm and its height is 21 cm. Find its (i) curved surface area (ii) total surface area and (iii) volume.
Height (h) = 21 cm
(i) Curved surface area = 2
(ii) Total surface area =
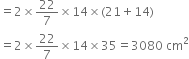
(iii) Volume =
A hollow cylindrical copper pipe is 21 dm long. Its outer and inner diameters are 10 cm and 6 cm respectively. Find the volume of copper used in making the pipe.
Volume of copper used in making the pipe = volume of the outer cylinder
– volume of the inner cylinder = ![]() R2h –
R2h – ![]() r2h
r2h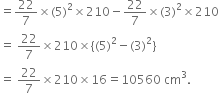
A powder tin has a square base with side 8 cm and height 13 cm. Another is cylindrical with the radius of its base 7 cm and its height 15 cm.
Find the difference in their capacities. ![]()
For a powder tin with a square base
Side of the square base = 8 cm Height = 13 cm
∴ Volume (v1) = 8 x 8 x 13 = 832 cm3 For a cylindrical powder tin
Radius of the base (r) = 7 cm Height (h) =15 cm
∴ Volume (v2) = ![]() r2h
r2h![]()
∴ Difference in their capacities = v2 – v1 = 2310 – 832 = 1478 cm3.
The area of the base of a right circular cylinder is 15400 cm2 and its volume is 92400 cm3. Find the height of the cylinder and also find curved surface of the cylinder.
Then,
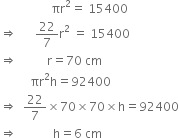
Hence, the height of the cylinder is 6 cm. Also, curved surface area of the cylinder = 2πrh
A square piece of paper of side 22 cm is rolled to form a cylinder. Find the volume of the cylinder.![]()
Let the base radius and height of the cylinder be r cm and h cm respectively.
Then,
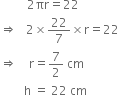
![]() Volume of the cylinder =
Volume of the cylinder = ![]()
![]()
A cylindrical container of base radius 28 cm contains sufficient water to submerge a rectangular block of iron with dimensions 32 cm x 22 cm x 14 cm. Find the rise in the level of water, when the block is completely submerged.
Let the rise in the level of water be h cm.
Then,
Volume of water displaced
= Volume of block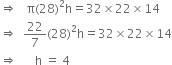
Hence, the rise in the level of water is 4 cm.
A river 4 m deep and 60 m wide is flowing at the rate of 0.31 km/hour. How much water will fall into the sea in a minute?
0.31 km/hour
= 0.31 x 1000 m/hour = 310 m/hour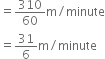
∴ Volume of water that falls into the sea in a minute![]()
A rectangular piece of paper is 22 cm long and 12 cm wide. A cylinder is formed by rolling the paper along its length. Find the volume of the cylinder.
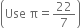
When the rectangular piece of paper is rolled along its length, then the length of the piece forms the circumference of the base and the breadth of the piece becomes the height of the cylinder.
Let the base radius and height of the cylinder be r cm and h cm respectively.
Then,![]()
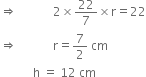
![]() Volume of the cylinder =
Volume of the cylinder = ![]()
= ![]()
= 4622
A well with 10 m inside diameter is long 14 m deep. Earth taken out of it is spread all around it to a width of 5 m to form an embankment. Find the height of the embankment.
(r) =
Depth of the wall (h) = 10 m Volume of the earth dug out = Volume of the well = π r2h = π(5)2(10) = 250π m3 Radius of the well with embankment (R)
= 5 + 5 = 10 m π Area of the embankment
= Area of the well with embankment
– Area of the well without embankment = πR2 – πr2 = π(R + r) (R – r)
= π(10 + 5) (10 – 5)
= 75π m2
∴ Height of the embankment![]()
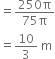
What is the mass of a metallic hollow cylindrical pipe 24 cm long with internal diameter 10 cm and made up of metal 5 mm thick. Density of the metal is 7 g per cm3.
Internal radius (r) = ![]()
Thickness = 5 mm = ![]()
![]() External radius (R) = 5 + 0.5 = 5.5 cm
External radius (R) = 5 + 0.5 = 5.5 cm
Length (h) 24 cm![]() Volume =
Volume = ![]()
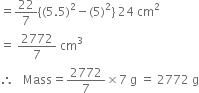
1.1 cu.cm of copper is to be drawn into a cylindrical wire 0.5 cm in diameter. Calculate the length of the wire.
Radius (R) =
Let the length of the wire be h cm. Then, volume of the wire
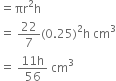
According to thr question
The difference between outside and inside surface of a cylindrical metallic pipe 14 cm long is 44 cm2. If the pipe is made of 99 cm3 of metal, find the outer and inner radii of the pipe.
and,
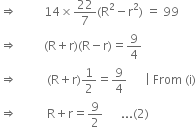
Solving (1) and (2), we get
Rain water which falls on a flat rectangular surface of length 6 cm and breadth 4 m is transferred into a cylindrical vessel of internal radius 20 cm. What will be the height of water in the cylindrical vessel if the rain fall is 1 cm? Give your answer to the nearest whole number. (Use  = 3.14)
= 3.14)

Let the height of water in the cylindrical vessel be h cm, Then,
Volume of water in the cylindrical vessel = π(20)2 h cm3 According to the question,![]()
![]()
t a Ramzan Mela, a stall keeper is one of the food stalls has a large cylindrical vessel of base radius 15 cm filled up to a height of 32 cm with orange juice. The juice is filled in small cylindrical glasses of radius 3 cm up to a height of 8 cm, and sold for र 3 each. How much money does the stall keeper receive by selling the juice completel?

Solution not provided.
Ans. र 300
The volume of a right circular cylinder is 1100 cm3 and the radius of its base is 5 m. Find its curved surface area.![]()
Solution not provided.
Ans. 220 cm2
The volume of a cylinder is 448π cubic cm and the height is 7 cm. Find its total surface area.
Solution not provided.
Ans. 240 p cm2
The outer and inner radii of a hollow copper cylinder of height 6 cm are 11 cm and 10 cm. Find the volume of the copper used.
Solution not provided.
Ans. 396 cm3
Volume of a right circular cylinder is 1100 cm3 and the radius of its base is 5 cm. Find its curved surface area.
Solution not provided.
Ans. 440 cm2
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio of 5 : 3. Find the ratio of their volumes
Solution not provided.
Ans. 20 : 27
A bag of grains contains 2.8 m3 of grain. How many bags of grain are needed to fill a right circular cylindrical drum of radius 4.2 m and height 5 m?
Solution not provided.
Ans. 99
The volume of a right circular cylinder is 3850 cm3. Find its height if its, diameter is 14 cm.
Solution not provided.
Ans. 25 cm
The total surface area of a cylinder of radius 7 cm is 880 m2. Find the height and the volume of the cylinder.
Solution not provided.
Ans. 13 cm, 2002 cm3.
Find the volume of the right circular cone with
(i) radius 6 cm, height 7 cm
(i) r = 6 cm
h = 7 cm![]() Volume of the right circular cone =
Volume of the right circular cone = ![]()
![]()
Find the volume of the right circular cone with
(ii) radius 3.5 cm, height 12 cm.
(ii) r = 3.5 cm
h = 12 cm
Find the capacity in litres of a conical vessel with
(i) radius 7 cm, slant height 25 cm
(i) r = 7 cm
l = 25 cm r2 + h2 = l2 ⇒ (7)2 + h2 = (25)2 ⇒ h2 = (25)2 – (7)2![]() h2 = 625 - 49
h2 = 625 - 49![]() h2 = 576
h2 = 576![]() h =
h = ![]()
![]() h = 24 cm
h = 24 cm![]() Capacity =
Capacity = ![]()
![]()
Find the capacity in litres of a conical vessel with
(ii) height 12 cm, slant height 13 cm.
(ii) h = 12
l = 13 cm
r2 + h2 + l2 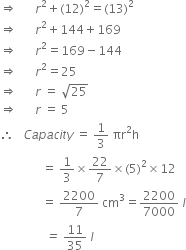
The height of a cone is 15 cm. If its volume is 1570 cm3, find the radius of the base. (Use  = 3.14)
= 3.14)
Let the radius of the base of the cone be r cm.
h = 15 cm Volume = 1570 cm3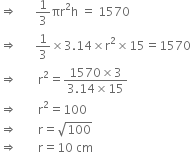
Hence, the radius of the base of the cone is 10 cm.
If the volume of a right circular cone of height 9 cm is 48π cm3, find the diameter of its base.
Let the radius of the base of the right circular cone be r cm.
h = 9 cm Volume = 48π cm3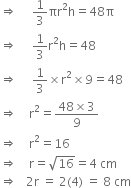
Hence, the diameter of the base of the right circular cone is 8 cm.
A conical pit of top diameter 3.5 m is 12 m deep. What is its capacity in kilolitres?
For conical pit
Diameter = 3.5 cm![]() Radius (r) =
Radius (r) = ![]()
Depth (h) = 12 m![]() Capacity of the conical pit =
Capacity of the conical pit = ![]()
![]()
= 38.5 m3 = 38.5 x 100 l
= 38.5 kl.
The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find
(i) height of the cone,
(ii) slant height of the cone,
(iii) curved surface area of the cone.
Let the height of the cone be h cm.
Volume = 9856 cm3
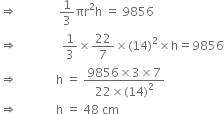
Hence, the height of the cone is 48 cm.
(ii) r = 14 cm
h = 48 cm
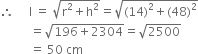
Hence, the slant height of the cone is 50 cm.
(iii) r = 14 cm
I = 50 cm
∴ Curved surface area = πrl![]()
Hence, the curved surface area of the cone is 2200 cm2.
A right triangle ABC with sides 5 cm, 12 cm and 13 cm is revolved about the side 12 cm. Find the volume of the solid so obtained.
The solid obtained will be a right circular cone whose radius of the base is 5 cm and height is 12 cm.
∴ r = 5 cm h = 12 cm
![]() Volume =
Volume = ![]()
= ![]()
Hence, the volume of the solid so obtained is 100 ∴ cm3.
If the triangle ABC in the Question 7 above is revolved about the side 5 cm, then find the volume of the solid so obtained. Find also the ratio of the volumes of the two solids obtained in Question 7 and 8.
The solid obtained will be a right circular cone whose radius of the base is 12 cm and height is 5 cm.
∴ r = 12 cm h = 5 cm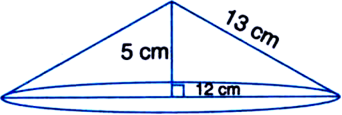
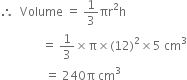
Ratio of the volumes of the two solids obtained = 100
∴: 240
∴ = 5 : 12
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m. Find its volume. The heap is to be covered by canvas to protect it from rain. Find the area of the canvas required.
For heap of wheat
Diameter = 10.5 m![]() Radius (r) =
Radius (r) = ![]()
Height (h) = 3 m![]() Volume =
Volume = ![]()
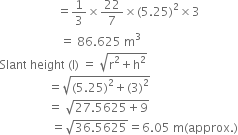
![]() Curved surface area =
Curved surface area = ![]()
![]()
Hence, the area of the canvas required is 99.825 m2. .
The radius of a sphere is 3.2 cm. Its surface area is
-
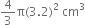
-
4
 (3.2)3 cm3
(3.2)3 cm3
-
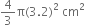
-
4
 (3.2)2 cm2.
(3.2)2 cm2.
D.
4
The total surface area of a cone of radius ‘2r’ and slant height 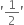 is:
is:
-
2
 r (l + r)
r (l + r)
-
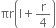
-
 r (4 r + l)
r (4 r + l)
-
2
 r
r
C.
The total surface area of a right circular cylinder is:
-
2πrh unit2
-
2πr (r + h) unit2
-
πr (2h + r) unit2
-
πr (l + r) unit2
B.
2πr (r + h) unit2The radius of the base and the height of a right circular cone are 7 cm and 24 cm respectively. Find the volume and total surface area of the cone.
and, total surface area of the cone = πr(l + r)
If the radius of the base of a right circular cone is halved keeping the height same, what is the ratio of the volume of the reduced cone to that of the original one?
Let the radius of the base and the height of the original cone be r and h respectively.
∴ Volume of the original cone (v1)
![]()
For the reduced cone
Radius = ![]()
Height = h![]() Volume of the reduced cone (v2)
Volume of the reduced cone (v2)
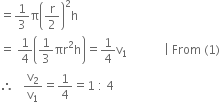
Hence, the ratio of the volume of the reduced cone to that of the original one is 1 : 4.
The base radii of the two right circular cones of the same height are in the ratio 3 : 5. Find the ratio of their volumes.
Let the base radii of the two right circular cones be 3x and 5x respectively.
Let their common height be h. Then,
Volume of the first cone (v1) = ![]()
![]()
and, volume of the second cone (v2) = ![]()
![]()
![]() Ratio of their volumes
Ratio of their volumes
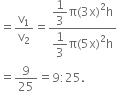
If h, c, v are respectively the height, curved surface and the volume of a cone, prove that 3πvh3 – c2h2 + 9v2 = 0
Let the base radius and the height of the cone be r and h respectively.
Let the slant height of the cone be l.
Then,
c = ![]() rl
rl
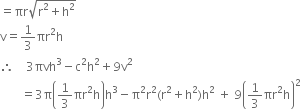
= π2r2h2 – π2r4h2 – π2r4 + π2r4h4 = 0
A vessel is in the shape of a cone. Radius of the broader end is 2.1 cm and height is 20 cm. Find the volume of the vessel.
r = 2.1 cm
h = 20 cm
∴ Volume of the vessel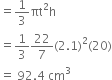
The radius and height of a right circular cone are in the ratio of 5 : 12. If its volume is 314 cm3, find the slant height and radius of the cone, ( = 3.14)
= 3.14)
Let the radius and height of the cone be 5k and 12k respectively. Then,
r = 5k
h = 12k
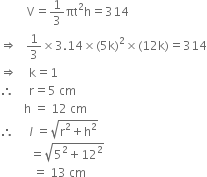
Hence, the slant height and radius of the cone are 13 cm and 5 cm respectively.
A conical tent is to accommodate 11 persons. Each person must have 4 square metre of the space on the ground and 20 cubic metres of air to breath. Find the height of the cone.
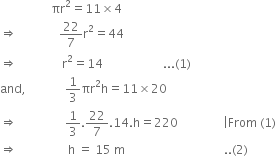
Hence, the height of the cone is 15 m.
A conical vessel whose internal radius is 5 cm and height 63 cm is full of oil. Find the the volume of the oil. If that oil is emptied into a cylindrical vessel with internal radius 10 cm, find the height of the oil in the cylindrical vessel.
For conical vessel
r = 5 cm h = 63 cm
∴ Volume of the oil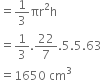
Let the required height be 4 cm. Then, according to the question, π(10)2H = 1650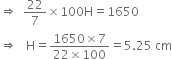
A semi-circular sheet of metal of diameter 28 cm is bent to form an open conical cup. Find the capacity of the cup.
Let the base radius of the cup be r cm. Then,
2nr = π x 14![]()
Let the height of the cup be h cm. Then\
l2 + r2 + h2![]()
![]() Capacity of the cup
Capacity of the cup
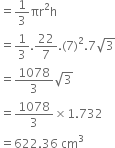
Find the volume of the largest right circular cone that can be placed in a cube of edge 7 cm.
Base radius (r) =
Height (h) = 7 cm
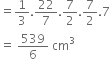
The height and the slant height of a cone are 21 cm and 28 cm respectively. Find the volume of the cone.
Solution not provided.
Ans. 7546 cm3
Monica has a piece of canvas whose area is 551 m2. She uses it to have a conical tent made, with a base radius of 7 m. Assuming that all the stitching margins and the wastage incurred while cutting, amounts to approximately 1 m2, find the volume of the tent that can be made with it.
Solution not provided.
Ans. 1232 m3
The ratio of the volumes of two cones is 4 : 5 and the ratio of their base radii is 2 : 3. Find the ratio of their vertical heights.
Solution not provided.
Ans. 9 : 5
The radius and height of a cone are in the ratio 3 : 4. If its volume is 301.44 cu. cm., find its radius and slant height. (Take  = 3.14)
= 3.14)
Solution not provided.
Ans. 6 cm, 10 cm
The radius and height of a right circular cone are in the ratio of 5 : 12 and its volume is 2512 cm3. Find the slant height and radius of base of cone. (Take  = 3.14)
= 3.14)
Solution not provided.
Ans. 26 cm, 10 cm
A cone of base radius 7 cm has a curved surface area 550 cm2. Find its volume.
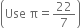
Solution not provided.
Ans. 1232 cm3
Find the capacity in litres of a conical vessel whose base diameter is 14 cm and slant height is 25 cm.
Solution not provided.
Ans. 1.232l
The volume of a cone of base radius 3 cm is 12 π cm3. Find the slant height of the cone.
Solution not provided.
Ans. 5 cm
The height and radius of a cone are in the ratio 4 : 3. If its volume is 96n cm3, find the slant height of the cone.
Solution not provided.
Ans. 10 cm.
The radius and height of a right circular cone are in the ratio 5 : 12. If its volume is 314 cm3, find the slant height and curved surface area. (Use  = 3.14)
= 3.14)
Solution not provided.
Ans. 13 cm, 65![]()
A heap of wheat is in the form of a cone whose diameter is 10.5 m and height is 3 m, find its volume.
Solution not provided.
Ans. 49.125 m3
Find the volume of a right circular cone whose slant height is 13 cm and the diameter of the base is 10 cm. (Take  = 3.14)
= 3.14)
Solution not provided.
Ans. 314 cm3
Find the amount of water displaced by a solid spherical ball of diameter
28 cm
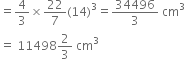
Find the amount of water displaced by a solid spherical ball of diameter
0.21 m.
The diameter of a metallic ball is 4.2 cm. What is the mass of the ball, if the density of the metal is 8.9 g per cm3?
Density = 8.9 g per cm3
Mass of the ball = Volume x Density
= 38.808 x 8.9 = 345.39 g (approx.).
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
Let the radius of the earth be r.
Then, diameter of the earth = 2r![]() Diameter of the moon
Diameter of the moon ![]()
![]() Radius of the moon =
Radius of the moon = ![]()
Volume of the earth (v1) = ![]()
Volume of the moon (v2)![]()
![]() (volume of the earth)
(volume of the earth)
Hence, the volume of the moon is ![]() th fraction of the volume of the earth.
th fraction of the volume of the earth.
How many litres of milk can a hemispherical bowl of diameter 10.5 cm hold?
Diameter = 10.5 cm![]() Radius (r) =
Radius (r) = ![]()
= 0.303 l (approx.)
A hemispherical tank is made up of an iron sheet 1 cm thick. If the inner radius is 1 m, then find the volume of the iron used to make the tank.
Inner radius (r) = 1 m Thickness of iron sheet = 1 cm = 0.01 m
∴ Outer radius (R) = Inner radius (r) + Thickness of iron sheet = 1 m + 0.01 m = 1.01 m
∴ Volume of the iron used to make the tank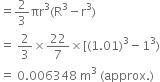
Find the volume of a sphere whose surface area is 154 cm2.
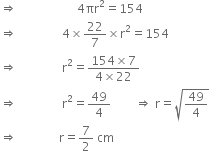
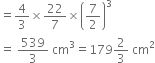
A dome of a building is in the form of a hemisphere. From inside, it was white-washed at the cost of र 498.96. If the cost of white-washing is र2.00 per square metre, find the
(i) inside surface area of the dome,
(ii) volume of the air inside the dome.
(ii) Let the radius of the hemisphere be r m. Inside surface area = 249.48 m2 ⇒ 2πr2= 249.48
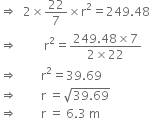
Twenty seven solid iron spheres, each of radius r and surface area S are melted to form a sphere with surface area S'. Find the
(i) radius r´ of the new sphere,
(ii) ratio of S and S’.
∴ Volume of 27 solid iron spheres =
∴ Volume of the new sphere = 36πr3 Let the radius of the new sphere be r’. Then,
Volume of the new sphere
According to the question,
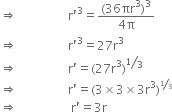
Hence, the radius r’ of the new-sphere is 3r.
(ii) S = 4πr2 S’ = 4π(3r)2
Hence, the ratio of S and S’ is 1 : 9.
A capsule of medicine is in the shape of a sphere of diameter 3.5 mm. How much medicine (in mm3) is needed to fill this capsule?
Capacity of the capsule
Hence, 22.46 mm3 (approx.) of medicine is needed to fill this capsule.
If the number of square centimetres on the surface of a sphere is equal to the number of cubic centimetres in its volume, what is the diameter of the sphere?
and, volume=
According to the question,
Hence, the diameter of the sphere is 6 cm.
A cone and a hemisphere have equal bases and equal volumes. Find the ratio of their heights.
Volume of the cone =
Volume of the hemisphere =
Acording to the question,
⇒ h = 2r
⇒ Height of the cone = 2r cm.
Height of the hemisphere = r cm.
∴ Ratio of their heights = 2r : r = 2 : 1.
Find the volume of a sphere whose surface area is 55.44 cm2. 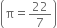
Let the radius of the sphere be r cm.
Then,
4πr2 = 55.44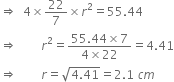
![]() Volume of the sphere =
Volume of the sphere = ![]()
![]()
= 38.808 cm3
A cube of side 4 cm contains a sphere touching its sides. Find the volume of the gap in between.
Radius of sphere (r) =
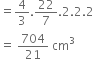
The outer diameter of a spherical shell is 10 cm and the inner diameter is 8 cm. Find the volume of the metal contained in the shell.
Outer radius (R) = ![]()
Inner radius (r) = ![]()
∴ Volume of the metal contained in the shell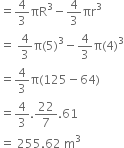
Three solid spheres of iron whose diameters are 2 cm, 12 cm and 16 cm respectively are melted into a single solid sphere. Find the radius of the solid sphere.
Let the radius of the solid sphere be R cm.
Then, according to the question,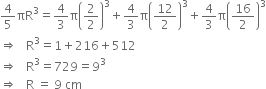
Hence, the radius of the solid sphere is 9 cm.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2 : 3.
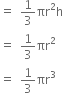
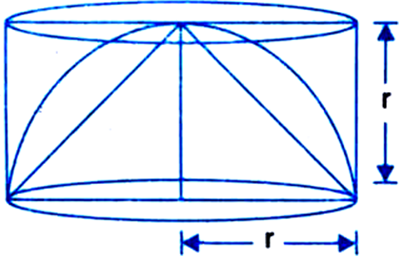
V2 = Volume of the hemisphere
V3 = Volume of the cylinder = πr2h = πr2r = πr3r
= 1 : 2 :3
A spherical ball of lead 3 cm in radius is melted and recast into three spherical balls. If the radii of two balls are  cm and 2 cm, find the diameter of the third ball.
cm and 2 cm, find the diameter of the third ball.
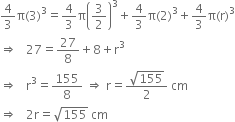
Hence, the diameter of the third ball is
The volumes of two spheres are in the ratio 64 : 27. Find the difference of their surface areas, if the sum of their radii is 7 cm.
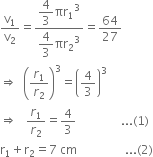
From (1) and (2)
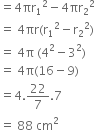
A hemispherical bowl of internal diameter 36 cm contains a liquid. This liquid is to be filled in cylindrical bottles of radius 3 cm and height 6 cm. How many bottles are required to empty the bowl?

Radius (R) =
For bottle
r = 3 cm h = 6 cm
∴ Volume = ![]()
= π (3)2 (6) cm3 Let n bottles be required. Then,![]()
A hemispherical bowl is made of steel 0.25 cm thick. The inner radius of the bowl is 5 cm. Find the outer curved surface area of the bowl.
Thickness of bowl = 0.25 cm Inner radius of bowl = 5 cm
∴ Outer radius of bowl
= 5 cm + 0.25 cm = 5.25 cm
∴ Outer curved surface area of the bowl = 2πr2![]()
= 33 cm2
A spherical iron shell with 8 cm external diameter weighs ![]()
Find the sick ness of the shell if the density of metal is 12 g/cm3 .
External radius =
Volume of metal =
According to the question,
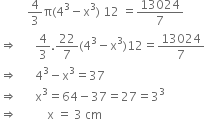
A shot-put is a metallic sphere of radius 4.9 cm. If the density of the metal is 7.8 g per cm3, find the mass of the shot-put.
Solution not provided.
Ans. 3.85 kg (nearly)
A hemispherical bowl has a radius of 3.5 cm. What would be the volume of water it would contain?
Solution not provided.
Ans. 89.8 cm3
The volumes of two spheres are in the ratio of 64 : 27. Find their radii if the sum of their radii is 21 cm.
Solution not provided.
Ans. 12 cm, 9 cm
A hemispherical shaped container has curved surface area of 2772 cm2. Find the capacity of container.
Solution not provided.
Ans. 19404 cm3
Find the volume of a sphere whose surface area is 154 cm2. Also, find the cost of polishing its surface @ र 5 per cm2.
Solution not provided.
The largest sphere is carved out of a cube of side 7 cm. Find the volume of the sphere.
Solution not provided.
Find the volume of metal used to construct a hollow sphere of internal and external diameters as 10 cm and 13 cm respectively.
Solution not provided.
The circumference of the cross-section of a hemispherical bowl is 132 cm. Find the capacity of the bowl.
Solution not provided.
The radius and height of a right circular cylinder are in the ratio of 2 : 3. If the volume of the cylinder is 1617 cm3, then find the radius and height of the cylinder.
Solution not provided.
Ans. 7 cm, 10.5 cm
The height of a right circular area is 16 cm and its base radius is 12 cm. Find the total surface area and volume of the cone in terms of  .
.
Solution not provided.
Ans. 672 ![]() cm2, 230
cm2, 230![]() cm3
cm3
The curved surface area of a cone is 308 cm2 and its slant height is 14 cm. Find the (i) radius of base of the cone (ii) total surface area of the cone.
Solution not provided.
Ans. (i) 7cm (ii) 462 cm2
The total surface area of a cube is 726 cm2. Find its volume.
Solution not provided.
Ans. 1331 cm3
The areas of three adjacent faces of a cuboid are 15 sq cm, 20 sq cm and 12 sq cm. Find the volume of the cuboid.
Solution not provided.
Ans. 60 cm3
How many square meters of canvas is required for making a conical tent where height is 3.5 m and the radius of the base is 12 m?
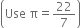
Solution not provided.
Ans. ![]()
The four of a rectangular hall has a perimeter 110 m. If the cost of painting the four walls at the rate of र 10 per m2 in र 13200, find the height of the hall.
Solution not provided.
Ans. 12 m
A hemispherical bowl made of brass has inner radius 10.5 cm. Find the cost of polishing it on the inside at the rate of र 0.12 per sq. cm.
Solution not provided.
Ans. र 8316
The curved surface area and volume of a pillar are 264 m2 and 396 m3respectively. Find the diameter and height of the pillar.
Solution not provided.
Ans. 6 m, 14 m
Find the volume of a cylindrical tank of height 1.4 m and circumference of base is 2π m.
Solution not provided.
Ans. 4.2 m3
A joker’s cap is in the form of a right circular cone of base radius 7 cm are height 24 cm. Find the area of sheet required to make 20 such caps.
Solution not provided.
Ans. 0.77 m3
A river 3 m deep and 40 m wide is fllowing at the rate of 2 km/hour. How much water will fall into the sea in 2 minutes.
Solution not provided.
Ans. 0.77 m3
A hollow right circular cylindrical copper pipe is 21 cm long. Its outer and inner diameters are 10 cm and 6 cm respectively. Find the volume of copper used in making the pipe.![]() .
.
Solution not provided.
Ans. 10560 cm3
The curved surface area of a cylindrical pillar is 264 m2 and its volume is 924 m3. Find the diam eter and height of the pillar.
Solution not provided.
Ans. 14 m, 7 m
Find the volume of the largest right circular cone that can be cut off from a cube where edge is 9 cm.
Solution not provided.
Ans. ![]()
Sheena has a piece of canvas, whose area is 550 m2. She uses it to have a conical tent made with a base radius 7 m. Find the volume of the tent that can be made with it.
Solution not provided.
Ans. 1232 m3
A match box measures 4 cm x 2.5 cm x 1.5 cm. What will be the volume of a packet containing 12 such boxes?
Solution not provided.
Ans. 180 cm3
Monica has a piece of canvas whose area is 818 m2. She uses it to have a conical tent made, with a base radius of 10 m. Assuming that all the stitching margin and the wastage incurred while cutting amounts to approximately 1.6 nr, find the volume of the tent that can be made with it.
Solution not provided.
Ans. 2512 m3
A wall 4 m long, 3 m height and 13 cm thick is made up of bricks each measuring 20 cm x 12 cm x 6.5 cm. Find the number of bricks required to build the wall.
Solution not provided.
Ans. 100000
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
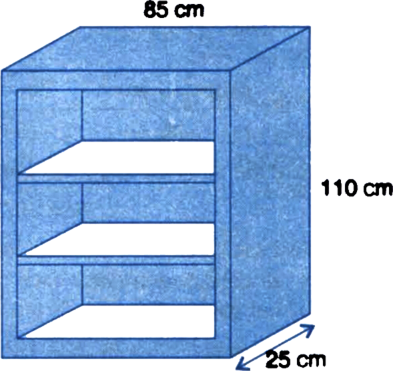
Surface area to be polished = [(110 x 85) + 2(110 x 25) + 2(85 x 25) + 2(110 x 5) + 4(75 x 5)]
= (9350 + 5500 + 4250 + 1100 + 1500) cm2 = 21700 cm2
∴ Expenses required for polishing @ 20 paise per cm2
= 21700 x 20 paise![]()
Surface area to be painted
= [2(20 x 90) + 6(75 x 20) + (75 x 90)]
= (3600 + 9000 + 6750) cm2 = 19350 cm2
∴ Expenses required for painting @ 10 paise per cm2
= 19350 x 10 paise![]()
∴ Total expenses required for polishing and painting the surface of the bookshelf
= र 4340 + र 1935 = र 6275.
The front compound wall of a house is decorated by wooden spheres of diameter 21 cm, placed on small supports as shown in figure. Eight such spheres are used for this purpose, and are to be painted silver. Each support is a cylinder of radius 1.5 cm and height 7 cm and is to be painted black. Find the cost of paint required if silver paint costs 25 paise per cm2 and black paint costs 5 paise per cm2.

For a wooden sphere
Diameter = 21 cm![]() Radius (r) =
Radius (r) = ![]()
∴ Surface area of a wooden sphere = 4![]()
∴ Surface area of a wooden sphere to be painted = 1386 – ![]() (1.5)2
(1.5)2![]()
∴ Surface area of eight wooden spheres = 1378.93 x 8 = 11031.44 cm2 Cost of painting silver @ 25 paise per cm2 = 11031.44 x 25 paise![]()
For a cylindrical support
Radius (r) = 1.5 cm Height (h) = 7 cm
Surface area of a cylindrical support = 2![]() rh
rh
![]()
∴ Surface area of eight cylindrical supports = 66 x 8 = 528 cm2
∴ Cost of painting black @ 5 paise per cm2 = 528 x 5 paise![]()
∴ Cost of paint required = 2757.86 + 26.40 = र 2784.26 (approx.)
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
This its diameter = 2
Curved surface area of the original sphere =
New diameter (decreased) of the sphere
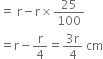
∴ Radius of the new sphere
∴ New curved surface area of the sphere
∴ Decrease in the original curved surface area
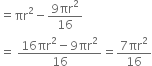
∴ Percentage of decrease in the original curved surface area
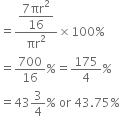
Hence, the original curved surface area decreases by 43.75%.
Find the mean of each of the following distributions :
(i)
|
xi |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
Total |
|
fi |
4 |
6 |
8 |
18 |
6 |
5 |
3 |
50 |
(ii)
|
xi |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
Total |
|
fi |
1 |
3 |
4 |
8 |
10 |
3 |
1 |
30 |
(iii)
|
xi |
50 |
75 |
100 |
125 |
150 |
175 |
200 |
Total |
|
fi |
12 |
18 |
50 |
70 |
25 |
15 |
10 |
200 |
(i)
|
xi |
fi |
fixi |
|
10 |
4 |
40 |
|
15 |
6 |
90 |
|
20 |
8 |
160 |
|
25 |
it |
450 |
|
30 |
6 |
180 |
|
35 |
5 |
175 |
|
40 |
3 |
120 |
|
Total |
50 |
1215 |
|
xi |
fi |
fixi |
|
12 |
1 |
12 |
|
13 |
3 |
39 |
|
14 |
4 |
56 |
|
15 |
8 |
120 |
|
16 |
10 |
160 |
|
17 |
3 |
51 |
|
18 |
1 |
18 |
|
Total |
30 |
456 |
(iii)
|
xi |
fi |
fixi |
|
50 |
12 |
600 |
|
75 |
18 |
1350 |
|
100 |
50 |
5000 |
|
125 |
70 |
8750 |
|
150 |
25 |
3750 |
|
175 |
15 |
2625 |
|
200 |
10 |
2000 |
|
Total |
200 |
24075 |
The following data have been overanged in ascending order. If the median of these data is 63, then find the value of x : 29, 32, 48, 50, x, x + 2, 72, 78, 84, 95

According to the question
Find the median of the following data:
95, 65, 75, 70, 75, 100, 50, 40.
Arranging the given data in the ascending order, we have
40, 50, 65, 70, 75, 75, 95,
100 Number of observations (n) = 8 which is even.
The mean of 40 observations was 160. It was detected on rechecking that the value 165 was wrongly copied as 125. Find the correct mean.
∵ Mean of 40 observations = 160
∴ Sum of 40 observations = 160 x 40 = 6400 Corrected sum of 40 observations
= 6400 - 125 + 165
= 6440![]() Correct mean =
Correct mean = ![]()
Mock Test Series
Sponsor Area
Sponsor Area