If the radius of the base of a right circular cone is halved keeping the height same, what is the ratio of the volume of the reduced cone to that of the original one?

Solution

Let the radius of the base and the height of the original cone be r and h respectively.
∴ Volume of the original cone (v₁)
$equals 1 third πr squared straight h space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$
For the reduced cone
Radius = $straight r over 2$
Height = h
$therefore$ Volume of the reduced cone (v₂)
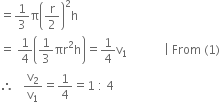
$equals 1 third straight pi open parentheses straight r over 2 close parentheses squared straight h equals space 1 fourth open parentheses 1 third πr squared straight h close parentheses equals 1 fourth straight v subscript 1 space space space space space space space space space space space space vertical line space From space left parenthesis 1 right parenthesis therefore space space space straight v subscript 2 over straight v subscript 1 equals 1 fourth equals 1 space colon space 4$
Hence, the ratio of the volume of the reduced cone to that of the original one is 1 : 4.

Some More Questions From Probability Chapter

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.

(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?

Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m × 3 m?

A table cover 4 m x 2 m is spread on a table. Find the cost of polishing the top of the table at र40 per square metre of 25 cm table cover is hanging all round the table.

A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.4 m and three windows each measuring 2 m x 1 m. The interior wall is to be colour washed. Find the cost of colour washing at the rate of र 3.50 per m².

For Daily Free Study Material Join wiredfaculty

Probability

If the radius of the base of a right circular cone is halved keeping the height same, what is the ratio of the volume of the reduced cone to that of the original one?

Some More Questions From Probability Chapter

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.

(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?

A table cover 4 m x 2 m is spread on a table. Find the cost of polishing the top of the table at र40 per square metre of 25 cm table cover is hanging all round the table.

A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.4 m and three windows each measuring 2 m x 1 m. The interior wall is to be colour washed. Find the cost of colour washing at the rate of र 3.50 per m².

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Probability

If the radius of the base of a right circular cone is halved keeping the height same, what is the ratio of the volume of the reduced cone to that of the original one?

Some More Questions From Probability Chapter

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high. (i) Which box has the greater lateral surface area and by how much?

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high. (i) Which box has the greater lateral surface area and by how much?

A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high. (i) What is the area of the glass?(ii) How much of tape is needed for all the 12 edges?

A table cover 4 m x 2 m is spread on a table. Find the cost of polishing the top of the table at र40 per square metre of 25 cm table cover is hanging all round the table.

A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.4 m and three windows each measuring 2 m x 1 m. The interior wall is to be colour washed. Find the cost of colour washing at the rate of र 3.50 per m2.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.

(i) What is the area of the glass?
(ii) How much of tape is needed for all the 12 edges?

A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.4 m and three windows each measuring 2 m x 1 m. The interior wall is to be colour washed. Find the cost of colour washing at the rate of र 3.50 per m².