If h, c, v are respectively the height, curved surface and the volume of a cone, prove that 3πvh3 – c2h2 + 9v2 = 0
Let the base radius and the height of the cone be r and h respectively.
Let the slant height of the cone be l.
Then,
c = ![]() rl
rl
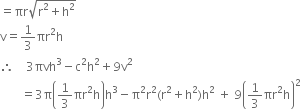
= π2r2h2 – π2r4h2 – π2r4 + π2r4h4 = 0



