Question
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2 : 3.
Solution
V1 = Volume of the cone
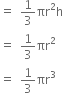
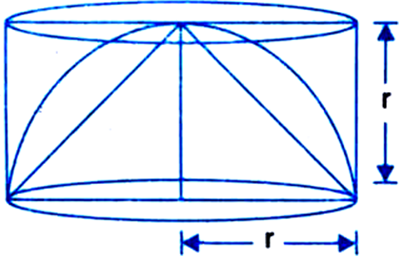
V2 = Volume of the hemisphere
V3 = Volume of the cylinder = πr2h = πr2r = πr3r
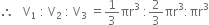
= 1 : 2 :3
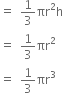

V2 = Volume of the hemisphere
V3 = Volume of the cylinder = πr2h = πr2r = πr3r
= 1 : 2 :3



