Question
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
Solution
Let the radius of the sphere be 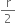 cm.
cm.
This its diameter = 2
Curved surface area of the original sphere =
New diameter (decreased) of the sphere
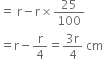
∴ Radius of the new sphere
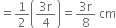
∴ New curved surface area of the sphere
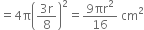
∴ Decrease in the original curved surface area
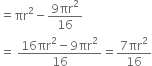
∴ Percentage of decrease in the original curved surface area
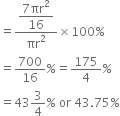
Hence, the original curved surface area decreases by 43.75%.
This its diameter = 2
Curved surface area of the original sphere =
New diameter (decreased) of the sphere
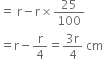
∴ Radius of the new sphere
∴ New curved surface area of the sphere
∴ Decrease in the original curved surface area
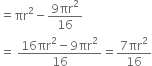
∴ Percentage of decrease in the original curved surface area
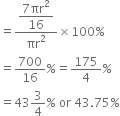
Hence, the original curved surface area decreases by 43.75%.



