+91-8076753736[email protected]
logo
logo
-->

Probability

Question
CBSEENMA9003560
Wired Faculty App

The volume of a right circular cone is 9856 cm3. If the diameter of the base is 28 cm, find

(i)     height of the cone,
(ii)    slant height of the cone,
(iii)    curved surface area of the cone.

Solution
(i) Diameter of the base = 28 cm
therefore    Radius of the base (r) = 28 over 2 space cm space equals space 14 space cm
Let the height of the cone be h cm.
Volume = 9856 cm3
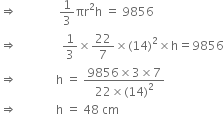
rightwards double arrow space space space space space space space space space space space space space space 1 third πr squared straight h space equals space 9856 rightwards double arrow space space space space space space space space space space space space space space space 1 third cross times 22 over 7 cross times left parenthesis 14 right parenthesis squared cross times straight h equals 9856 rightwards double arrow space space space space space space space space space space space space space straight h space equals space fraction numerator 9856 cross times 3 cross times 7 over denominator 22 cross times left parenthesis 14 right parenthesis squared end fraction rightwards double arrow space space space space space space space space space space space space space straight h space equals space 48 space cm space
Hence, the height of the cone is 48 cm.
(ii)   r = 14 cm
       h = 48 cm
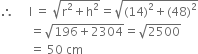
therefore space space space space space straight l space equals space square root of straight r squared plus straight h squared end root equals square root of left parenthesis 14 right parenthesis squared plus left parenthesis 48 right parenthesis squared end root space space space space space space space space space space equals square root of 196 plus 2304 end root equals square root of 2500 space space space space space space space space space space equals space 50 space cm

Hence, the slant height of the cone is 50 cm.
(iii) r = 14 cm
I = 50 cm
∴ Curved surface area = πrl
equals 22 over 7 cross times 14 cross times 50 equals 2200 space cm squared

Hence, the curved surface area of the cone is 2200 cm2.

Some More Questions From Probability Chapter

A plastic box 1.5 m long, 1.25 m wide and 65 cm deep is to be made. It is opened at the top. Ignoring the thickness of the plastic sheet, determine:

(i) The area of the sheet required for making the box.
(ii) The cost of sheet for it, if a sheet measuring 1 m2 costsर 20.

The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of र 7.50 per m2.

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.

(i)    What is the area of the glass?
(ii)    How much of tape is needed for all the 12 edges?

Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m × 3 m?

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation