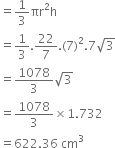+91-8076753736 support@wiredfaculty.com
logo
logo

Sponsor Area

Probability

Question
CBSEENMA9003681
Wired Faculty App

A semi-circular sheet of metal of diameter 28 cm is bent to form an open conical cup. Find the capacity of the cup.

Solution
When a semi-circular sheet is bent to form an open conical cup, the radius of the sheet becomes the slant height of the cup and the circumference of the sheet becomes the circumference of the base of the cone.

therefore space space space space space space space space space space space space l italic space equals 28 over 2 space cm space equals space 14 space cm

Let the base radius of the cup be r cm. Then,
2nr = π x 14
rightwards double arrow space space space space space space 2.22 over 7. straight r equals 22 over 7.14 rightwards double arrow space space space space space space space space space space space space space space straight r equals 7 space cm
Let the height of the cup be h cm. Then\
             l2 + r2 + h2
rightwards double arrow space space space space space space space space space space space space left parenthesis 14 right parenthesis squared equals left parenthesis 7 right parenthesis squared plus straight h squared rightwards double arrow space space space space space space space space space space space space space space straight h equals 7 square root of 3 space cm
therefore  Capacity of the cup
              equals 1 third πr squared straight h equals 1 third.22 over 7. left parenthesis 7 right parenthesis squared.7 square root of 3 equals 1078 over 3 square root of 3 equals 1078 over 3 cross times 1.732 equals 622.36 space cm cubed

Sponsor Area

Some More Questions From Probability Chapter

The length, breadth and height of a room are 5 m, 4 m and 3 m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of र 7.50 per m2.

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A cubical box has each edge 10 cm and another cuboidal box is 12.5 cm long, 10 cm wide and 8 cm high.

(i) Which box has the greater lateral surface area and by how much?

A small indoor greenhouse (herbarium) is made entirely of glass panes (including base) held together with tape. It is 30 cm long, 25 cm wide and 25 cm high.

(i)    What is the area of the glass?
(ii)    How much of tape is needed for all the 12 edges?

Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m × 3 m?

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation