+91-8076753736 [email protected]

-->

Probability

Question

Wired Faculty App

A hemispherical bowl made of brass has inner diameter 10.5 cm. Find the cost of tin-plating it on the inside at the rate of ` 16 per 100 cm2.

Solution

Inner diameter = 10.5 cm

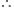therefore

Inner radius (r) =

fraction numerator 10.5 over denominator 2 end fraction space cm space equals space 5.25 space cm

Inner surface area = 2πr²

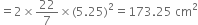
equals 2 cross times 22 over 7 cross times left parenthesis 5.25 right parenthesis squared equals 173.25 space cm squared

Cost of tin-plating at the rate of र 16 per 100 cm^{2
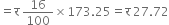
$equals straight र space 16 over 100 cross times 173.25 equals straight र space 27.72$}

Some More Questions From Probability Chapter

Parveen wanted to make a temporary shelter for her car, by making a box-like structure with tarpaulin that covers all the four sides and the top of the car (with the front face as a flap which can be rolled up). Assuming that the stitching margins are very small, and therefore negligible, how much tarpaulin would be required to make the shelter of height 2.5 m, with base dimensions 4 m × 3 m?

A table cover 4 m x 2 m is spread on a table. Find the cost of polishing the top of the table at र40 per square metre of 25 cm table cover is hanging all round the table.

A classroom is 7 m long, 6.5 m wide and 4 m high. It has one door 3 m x 1.4 m and three windows each measuring 2 m x 1 m. The interior wall is to be colour washed. Find the cost of colour washing at the rate of र 3.50 per m².

Two cubes of side 6 cm each, are joined end to end. Find the surface area of the resulting cuboid.

The dimensions of a rectangular box are in the ratio of 2 : 3 : 4 and the difference between the cost of covering it with sheet of paper at the rates of र 8 and र 9.50 per m² is र1248. Find the dimensions of the box.

The length, breadth and height of a cuboid are 15 cm, 10 cm and 20 cm. Find the surface area of the cuboid.

Mary wants to decorate her Christmas tree. She wants to place the tree on a wooden block covered with coloured paper with picture of Santa Claus on it (see figure). She must know the exact quantity of paper to buy for this purpose. If the box has length, breadth and height as 80 cm, 40 cm and 20 cm respectively how many square sheets of paper of side 40 cm would she require?

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation