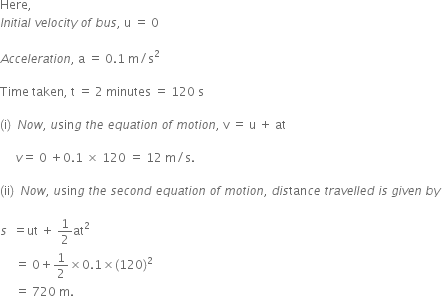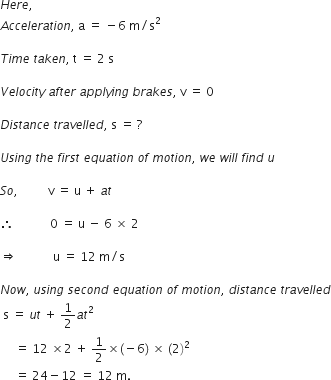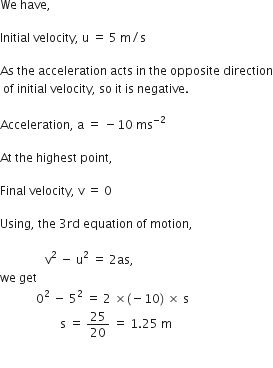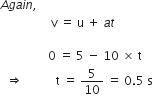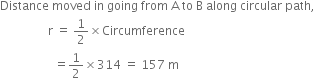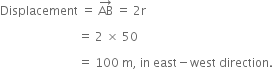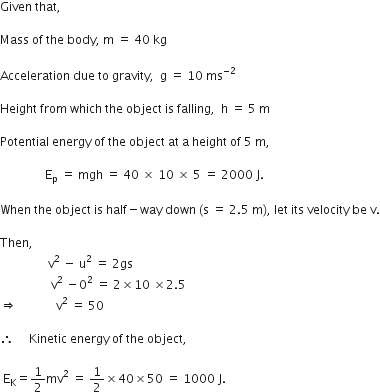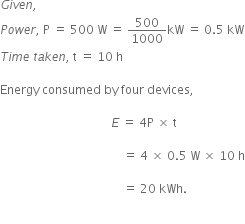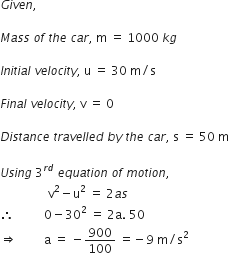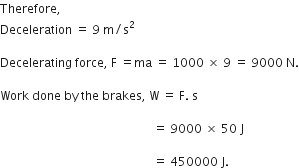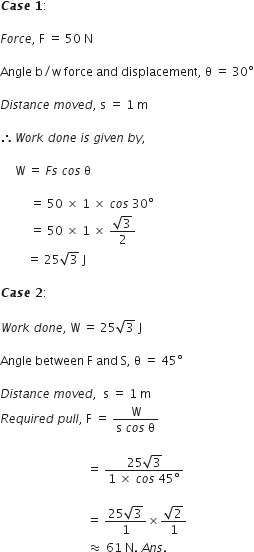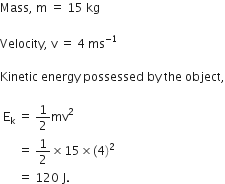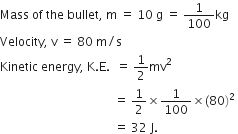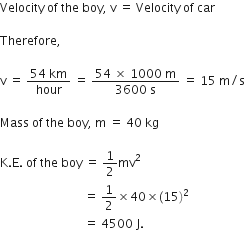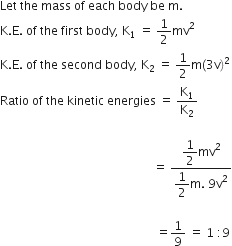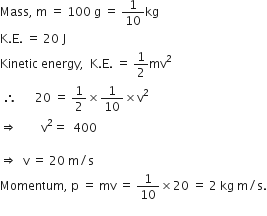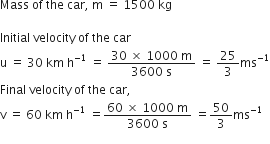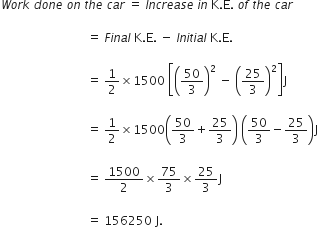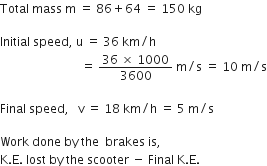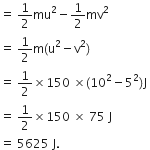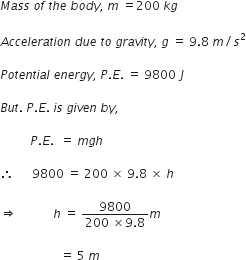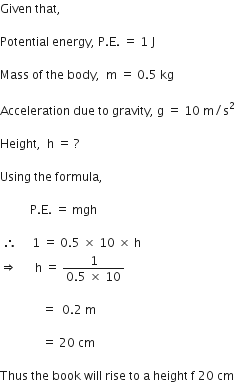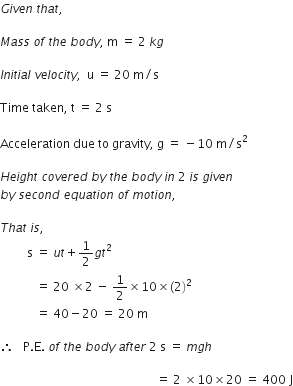Science Chapter 1 Matter In Our Surroundings
Sponsor Area
NCERT Solution For Class 9 About 2.html
Convert the following temperature to Celsius scale.
300K
To change a temperature on the kelvin scale to the celsius scale. Subtract 273 form given temperature.
300 K = 300 - 273 = 27°C
Convert the following temperature to Celsius scale.
573 K
573 K = 573 – 273 = 300°C
Convert the following temperatures to Kelvin scale
25°C
To change a temperature on the celsius to kelvin. Add 273 to given temperature. i.e.,
25°C = 25 + 273 = 298K
For any substance, why does the temperature remain constant during the change of state ?
During the change of state temperature remains constant because the heat given to the matter is used up in changing the state of matter. This is called latent heat.
Suggest a method to liquify atmospheric gases.
Liquefaction of gases is the process by which substances in their gaseous state are converted to the liquid state. When pressure on a gas is increased, its molecules closer together, and its temperature is reduced, which removes enough energy to make it change from the gaseous to the liquid state.
Convert the following temperatures to Kelvin scale.
35°C
To change a temperature on the celsius scale to kelvin scale. Add 273 to given temperature.
35°C = 35 + 273 = 308K
Give reason for the following observations.
Naphthalene balls disappear with time without leaving any solid.
Naphthalene shows the property of sublimation. Evaporation of naphthalene takes place easily and so it disappears during course of time without leaving any solid.
Give reason for the following observations.
We can get the smell of perfume sitting several metres away.
Perfume has high degree of vaporisation and its vapours diffuse into air easily. That is why we can smell perfume sitting several metres away.
What is the physical state of water at
a) 25°C
b)00C
c)1000C
(a)Liquid
(b) Solid and Liquid
(c) Liquid and Vapours
Give two reasons to justify
Water at room temperature is a liquid.
At room temperature water is a liquid because of the following characteristic of liquid:
1) At room temperature, water has no shape but a fixed volume that is, it occupies the shape of the container in which it is kept.
2) Water at room temperature is a liquid because it has fluidity.
Give two reasons to justify
An iron almirah is a solid at room temperature.
An iron almirah is a solid at room temperature because:
1) It has a definite shape and volume.
2) It is rigid at room temperature.
Why is ice at 273K more effective in cooling than water at the same temperature ?
Ice at 273 K is less energetic than water. It is because of the difference in the latent heat of fusion which is present in water at the same temperature in the form of extra energy.
What produces more severe burns, boiling water or steam ?
Steam produces more severe burns than boiling water. This is because steam has more energy than boiling water,present in it in the form of latent heat of vaporization.
8. Name A, B, C, D, E and F in the following diagram showing state change :
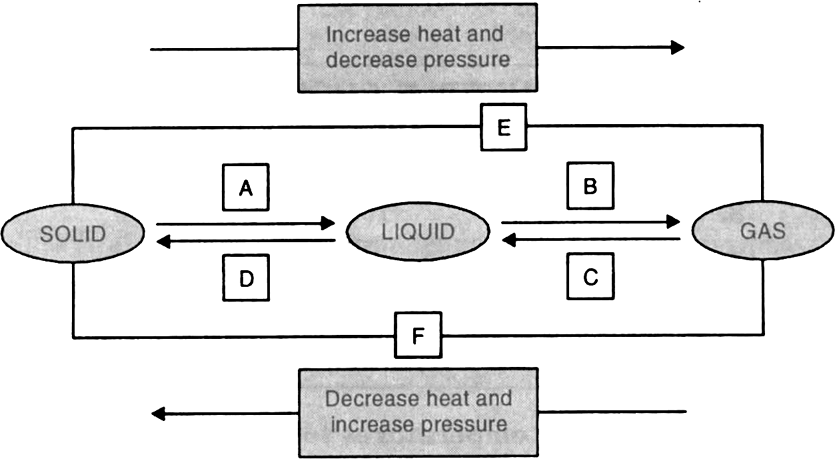
A — Melting
B — Evaporation
C — Liquefaction
D — Fusion
E — Sublimation
F — Solidification
Sponsor Area
Both boiling and evaporation convert a liquid into vapour. What is the difference between the two process
Evaporation is phase transition from liquid to vapour phase. It occur at temperatures below the boiling temperature at given temperature. Evaporation is a surface phenomenon.
Boiling is phase transition from liquid state to gas phase that occurs at or above the boiling point. Boiling is bulk phenomenon.
Define Evaporation
The phenomenon of change of a liquid into vapours at any temperature below its boiling point is called evaporation. For example if Water left in open vessel at room temperature disappears after some time due to evaporation.
Discuss the factors which affect evaporation
There are four factors which affect evaporation.
(a) Surface area. Evaporation is a surface phenomenon. Thus escaping of particles from liquid state to vapour state depends on surface area. Therefore, the rate of evaporation increases with surface area.
(b) Temperature of the system. With increase of surface temperature, the number of particles with larger kinetic energy increases and there is greater chance of escape of particles from liquid to vapour state. Therefore, rate of evaporation increases with temperature.
(c) Wind. More particles of liquid vapour would be carried away from the surface of the liquid with increasing speed of wind. Thus rate of evaporation increases with speed of wind.
(d) Humidity. Humidity is the amount of vapour present in the air. At a given temperature, air cannot hold more than a fixed amount of water vapour. Therefore, the rate of evaporation decreases with increase in the humidity of air.
Why does evaporation causes cooling of a liquid system
Due to evaporation, only high energy particles leave the surface. This results in decrease of average kinetic energy of the particles in the system. Kinetic energy is related to temperature. As a result there is a drop in temperature of the liquid. Thus evaporation causes cooling.
Why do wet clothes kept in shade dry slowly on a rainy day even in summer ?
During rainy day, the humidity of air increases, i.e., air is quite saturated with water vapour or air cannot hold more water vapour. Therefore, rate of evaporation of water from wet clothes decreases. So wet clothes dry slowly in rainy day.
Why do we see water droplets on the outer surface of a glass containing ice-cold water
The air around ice-cold water container contains water vapours which have higher energy than ice-cold water. Therefore, water vapour present in the air loses energy when come in contact with cold water. These are then converted into liquid state, which we see as water droplets.
Why should we wear cotton clothes in summer
In summer we feel hot. The body temperature should remain constant. In order to keep body cool, the water from the body gets evaporated and gets deposited on the body surface as sweat.
Cotton allows better air circulation, which helps in absorbing and removing body moisture caused by sweat. It therefore minimizes fungal breeding by keeping your body dry and cool. Therefore we should wear cotton clothes in summer.
How does our body maintain its temperature during summer
During summer, we perspire more because of the mechanism of our body which keeps us cool. During evaporation, the particle at the surface of the liquid gain energy from body surface and change into vapour phase. In this process the heat energy equal to latent heat of vaporization is absorbed from the body leaving the body cool.
Define (i) Latent heat of fusion and (ii) Latent heat of vaporisation
Latent heat of fusion is defined as the amount of energy required to convert of solid to liquid at 1 atmospheric pressure at constant temperature.
Latent heat of vaporsiation is defined as the amount of heat energy required to convert water to gas phase at 100°C and 1 atmosheric pressure.
Benzene is a liquid. At 80°C, liquid benzene is in equilibrium with its vapors. It is found that particles of benzene vapors are more energetic than particles of liquid benzene. Explain the observation.
Particles of benzene vapors are more energetic because of benzene vapours have gained extra energy in the form of latent heat of vaporisation. Hence it is more energetic.
What is the relation between boiling point of a liquid and the molecular forces of attraction between the particles of a liquid?
Boiling point of liquid depend on the intermolecular force, Stronger the intermolecular forces of attraction, higher would be the boiling point. For example, particles of alcohol have weaker intermolecular forces of attraction than of water particles. This is in conformity with the fact that alcohol boils at lower temperature, of 78°C as compared to boiling point of water which is 100°C.
Change the following temperatures to Kelvin scale.
1) 40°C
2) 80°C
3) 213°C
1) 40°C = 40 +273 = 313K
2) 80°C = 80 +273 =353K
3) 213°C = 213 +273=486K
Why is ice at 273K is less energetic than water at the same temperature
Cooling takes place when heat is removed from a system, in case of ice at 273 K, it will take latent heat from the medium to convert itself into water at 273K there will be a change in physical state, whereas in case of water at 273 K there will be no change in state. Hence lesser energy will be taken from the medium.
What is sublimation ? Give an example with illustration.
Generally matter changes its state on heating from solid to liquid and from liquid to gas. However, there are some substances that change directly from solid state to gaseous state and vice versa. This change of state from solid to gas without changing into liquid state or vice versa is called sublimation. For example, camphor on heating directly changes into vapors. Another example of Sublimation is ammonium chloride.
Illustration:
1) Take some ammonium chloride. Powder it and put in a China dish. Put an inverted funnel over the China dish. Put some cotton plug on the item of the funnel. Now heat the China dish .
2) You will notice fine crystal particles depositing on the inner walls of the funnel. Thus, on heating ammonium chloride is directly converted into ammonium chloride vapours which condense on the inner walls of the China dish.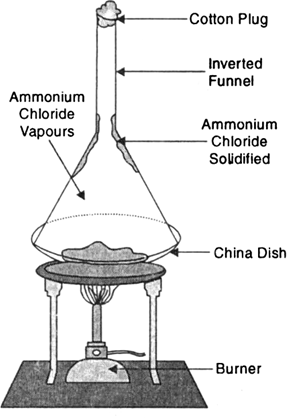
Fig. Sublimation of ammonium chloride.
Select the substances which follow the process of sublimation : Ice, ammonium chloride, salt, naphthalene, ghee, coconut oil, camphor.
Sublimation is the transition of a substance directly from the solid to the gas phase without passing through the intermediate liquid phase.
Ammonium chloride, naphthalene and camphor follow the process of sublimation.
Ghee freezes at room temperature and mustard oil does not (in winter). Which of these has a higher melting point and lower intermolecular forces
Ghee freezes at room temperature and mustard oil does not, it shows that intermolecular forces between particles of ghee are stronger compared to those of mustard oil. Higher the intermolecular forces, higher is the melting point. Therefore, ghee has a higher melting point than that of mustard oil.
Which of the following shows phenomenon of sublimation ? Solid water, solid carbon dioxide, solid alcohol, solid oxygen.
Sublimation is phenomenon in which solid phase is directly converted to liquid phase or vice versa.
Solid carbon dioxide.
What is the effect of temperature and pressure on a gas ?
At a given pressure, reduction of temperature liquefies a gas at some point. At a given temperature, increase of pressure also results in liquifying a gas.
How do you differentiate between a gas and a vapour ?
Vapour phase is not a state of matter. Vapour is a substance in the gas phase at a temperature lower than its critical point. it means that the vapour can be condensed to a liquid by increasing the pressure on it without reducing the temperature.
Gas is the state of matter distinguished from the solid and liquid state. Gas has relatively low density and viscosity, having great expansion and contraction which change with pressure and temperature.
How are particles of matter affected with increasing or reducing pressure on the matter at a given temperature ?
On increasing pressure, particles of a matter come closer and these move apart on reducing pressure at a given temperature. Thus if pressure is increasingly applied on a gas, particles of the gas come closer and closer and eventually the gas may change into liquid and then solid form. Fig. shows three cylinders in which a matter is present as gas, liquid and solid.
Changing state of matter on application of pressure : (a) solid; (b) liquid; (c) gas.
How do you define pressure ?
The pressure is the force per unit area exerted by a gas on the walls of the container. It is measured in atmospheres (atm) or Pascals (Pa) 1 atm = 1.01 x 105 Pa
What is atmospheric pressure ?
The pressure of air in atmosphere is called atmospheric pressure. It is 1 atmosphere at sea level and is also called normal atmospheric pressure.
The unit of pressure is Pascal (Pa). 1 atmosphere = 1.01 × 105 Pa.
Sponsor Area
Define Evaporation.
The phenomenon of change of a liquid into vapours at any temperature below its boiling point is called evaporation. For example if water left in open vessel at room temperature disappears after some time due to evaporation.
Why does evaporation causes cooling of a liquid system ?
Why does a desert cooler cool better on a hot dry day.
On a hot dry day, the rate of evaporation is direcrtly proportional to the temperature and inversely proportional to humidity. Therefore, On the hot dry day the rate of evaporation increase thus causing a cooling effect.
How does the water kept in an earthen pot (matka) become cool during summers ?
Earthen pots have small pores through which the water seeps and evaporation leads to cooling of the water.
Why does our palm feel cold when we put some acetone or petrol or perfume on it ?
Acetone, perfume and petrol are volatile liquids, i.e., they have low boiling points. When kept on palm, they can absorb enough energy from the palm or surroundings and evaporate and leave the palm cool.
Why are we able to sip hot tea or milk faster from a saucer rather than a cup ?
Hot tea or milk cover larger surface area on a saucer and resulting in increase of evaporation. The tea or milk thus cool faster on a saucer and we can sip it more comfortably.
What types of clothes should we wear during summer season ?
We should wear cotton clothes during summer season. Because during summer we perspire more to maintain the temperature of our body. Cotton is a good absorber of water (sweat). It then exposes the water to atmosphere for easy evaporation leaving us dry and cool.
What is plasma ?
Plasma is a state of matter in which the state consists of super energetic and super excited particles. These particles are in the form of ionised gases.
Is it true to say that fluorescent tube contains only plasma ? Explain.
It is not correct to say that fluorescent tube contains only plasma. Inside a fluorescent tube there is helium gas or some other gas. The gas gets ionised, that is, gets charged when electrical energy flows through it.
Why do the sun or the stars glow ?
Sun or the stars glow because at their core the pressure is so high that hydrogen fuses to create helium. This process releases a great amount of energy, which result in growing the sun or stars.
Do all particles or plasma glow similarly ?
The plasma glows with different colours depending on the nature of the containing gas. Neon sign bulb (containing neon gas) glows differently than a fluorescent tube (containing helium gas).
What is the difference between a gas and plasma ?
Gas consists of particles which are neutral and are associated with energies comparable with atmospheric temperature.
Plasma are super energenic particles in the form of ionized gases.
How can matter be classified on the basis of their physical nature ?
Matter can classified in three different states.
solid, liquid and gas.
These states of matter arise due to the variation in the characteristics of the particles of matter.
Which of the following substances is most compressible ?
Carbon dioxide, water, sodium chloride salt.
Carbon dioxide is most compressible becuase of the larger space between the molecule.
Which property of a gas results in study pressure of the gas ?
The constant bombardment of gas particles with the walls of the container of the ?as gives pressure of the gas.
In which of the following substances you expect weakest intermolecular forces ?
Water, methyl alcohol, iron, nitrogen gas.
Nitrogen gas has weakest intermolecular force.
Diffusion takes place fastest when two gases are brought in contact with each other ? Which characteristic of gases is responsible for this behaviour ?
Force of attraction between the gases molecule is very low. Therefore gases are in a state of constant rapid motion in all direction. This characteristic behaviour of gases responsible for diffusion.
Which states of matter take the shape of the containing vessel ?
Liquids and gases states of matter take the shape of the containing vessel depending upon condition.
A glass of water is heavier than when it is empty. What property of matter is signified by this observation ?
it signified that matter has mass.
When a spoon of matter like salt is poured in water. Soon salt disappears. What conclusion you can draw from this observation about the structure of matter ?
It manifest that particles of matter have space between them.
Which one of the following are a matter ?
Chair, air love smell, hate, almonds, thought, cold, cold drinks, smell of perfume
Matter: Chair, air, almonds, cold, drinks.
What name is given to the energy possessed by a particle due to its motion ?
The energy posses by a partcle due to its motion known as Kinetic energy.
Which combination of matter shows almost no diffusion ?
Solid-gas, solid-liquid, gas-gas, liquid-solid, solid-solid, liquid-liquid.
Solid-solid is combination of matter which shows no diffusion.
Which of the following matter has lowest density ?
Water, sugar, salt, ice.
Liquids generally have lower density as compared to solids. Density of water is the maximum at 4°C. The density of ice is less than that of the water. Thus, ice floats on water. Hence ice has lowest density.
State the property of matter that enables aquatic plants and animals survive in water
Diffusion of gases into water helps aquatic plants and animals to survive in water.
How does the rate of diffusion change with temperature ?
Kinetic energy of gas molecule increase with increasing temperature. Hence rate of difussion also increases with temperature.
At 0°C, when ice on heating changes into water, temperature remains constant. What is this heat as disappeared called ?
Latent heat of fusion.
Which of the following two processes is a bulk phenomenon ?
Boiling of a liquid, vaporisation of a liquid.
Boiling of a liquid is a bulk phenomenon.
Name the two parameters which determine the physical state of matter.
Temperature and pressure can determine the physical state of matter.
Which of the following does not influence evaporation of a liquid ?
Surface area, density, amount of liquid, wind speed, temperature of atmosphere.
Amount of liquid does not influence evaportion of a liquid.
What is normal atmospheric pressure ?
Atmospheric pressure at sea level is 1 atmosphere, and is taken as the normal atmospheric pressure. 1 atmosphere = 1.01 × 105 Pa.
Sponsor Area
The stronger the intermolecular force of attraction, the closer the _______________ space.
intermolecular
The state of matter can be changed by changing ____________ or ____________.
temperature
,pressure
Liquids have
Ffixed volume and fixed shape
Fixed shape and no fixed volume
Fixed volume and no fixed shape
Neither fixed volume nor fixed shape
C.
Fixed volume and no fixed shape
Materials existing as liquids have
boiling point and melting point above room temperature
boiling point and melting point below room temperature
- boiling point above room temperature and melting point below room temperature
boiling point and melting point above room temperature
C.
Gases are liquified under
High pressure, High temperature
High pressure, Low temperature
Low pressure, High temperature
Low pressure, Low temperature
B.
High pressure, Low temperature
Gases do not have
High compressibility
- High fluidity
High density
Large volume
C.
High density
Evaporation of a material takes place
Above its boiling point
Above its melting point
Below its boiling point
Below its melting point
C.
Below its boiling point
Particles of a liquid
Are most ordered
Move randomly
Have large intermolecular spaces
Can slip and slid over each other
D.
Can slip and slid over each other
The fluorescent tubes and neon sign bulbs glow because of
presence of charged particles
high density of gases
high temperature
high applied voltage
A.
presence of charged particles
Arrange the following substances in increasing order of forces of attraction between the particles — water, sugar, oxygen.
The intermolecular force of attraction is least in gas, followed by liquid and maximum in gas. Therefore it least in oxygen followed by water and maximum in sugar. Therefore the increasing order :
Oxygen<water<sugar
What do you mean by latent heat?
Latent heat define as the quantity of heat absorbed or released by a substance undergoing a change of state, such as At 0°C, when the ice melts, the temperature of the system does not change though the heat is continuously supplied. The given heat is used up in overcoming the force of intermolecular attraction. This results in the conversion of ice into water. As this heat energy is absorbed by ice without any rise in temperature of the system, this heat is considered as hidden in the system and is known as latent heat.
An athlete completes one round of a circular track of diameter 200 m in 40 s. What will be the distance covered and the displacement at the end of 2 minutes 20 s?
Diameter of circular track (D) = 200 m
Radius of circular track (r) = 200/2=100 m
Time taken by the athlete for one round (t) = 40 s
Distance covered by athlete in one round (s) = 2π r
= 2 × ( 22 / 7 )×100
Speed of the athlete (v) = Distance / Time
= (2 × 2200)/(7 × 40)
= 4400 / 7 × 40
∴ Distance covered in 2 minutes 20
seconds (s) or 140 s
= Speed (s) × Time(t)
= 4400 / (7 × 40) × (2×60 + 20)
= 4400 /( 7 × 40) × 140
= 4400 × 140 /7 × 40
=2200 m
Number of round in 40 s =1 round
Number of round in 140 s =140/40
=3.5 rounds
Joseph jogs from one end A to the other end B of a straight 300 m road in 2 minutes and 30 seconds and then turns around and jogs 100 m back to point C in another 1 minute. What are Joseph’s average speeds and velocities in jogging (a) from A to B and (b) from A to C?
Disatnce covered = 300 m
Time taken = 2 minutes 30 seconds = 2.50 = 150 s
Average speed =
=
Displacement = 300 m
So, average velocity =
=
ii) In the second case, there is motion from A to B to C,
Distance covered = 300+ 100 = 400 m
Displacement = AB - CB = 300 - 100 = 200 m
Time taken = 2.50 + 1.00 = 3.50 min = 3.5060 = 210 sec
So, Average speed =
=
Average velocity =
=
A driver of a car travelling at 52 km h–1 applies the brakes and accelerates uniformly in the opposite direction. The car stops in 5 s. Another driver going at 34 km h–1 in another car applies his brakes slowly and stops in 10 s. On the same graph paper, plot the speed versus time graphs for the two cars. Which of the two cars travelled farther after the brakes were applied?
Initial speed of car A = 52 km/hr
Time at which the car A comes to a stop = 5 s
Initial speed of car B = 34 km/h
Time at which the car B comes to rest = 10 s
Speed versus time graph for two cars: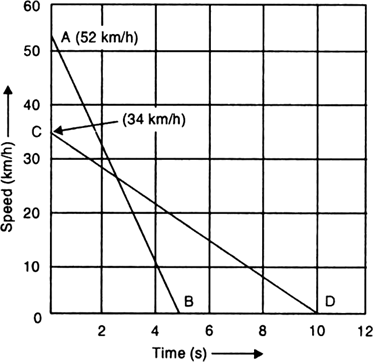
In Fig. AB and CD are the speed-time graphs for the two cars whose initial speeds are 52 km/h and , respectively.
Distance covered by first car before coming to rest is equal to Are of traingle AOB. 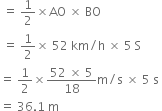
Distance covered by the second car before coming to rest is, 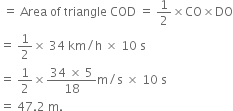
Thus, the second car travels farther than the first car after the brakes are applied.
Fig. shows the distance-time graph of three objects A, B and C. Study the graph and answer the following questions:
(a) Which of the three is travelling the fastest?
(b) Are all three ever at the same point on the road?
(c) How far has C travelled when B passes A?
(d) How far has B travelled by the time it passes C?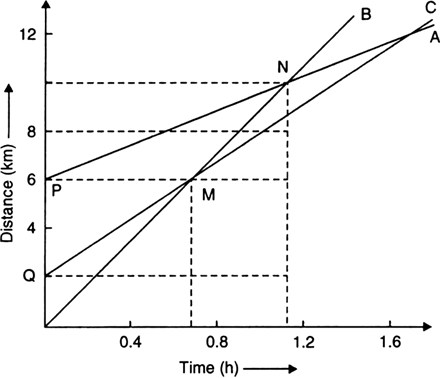

Thus, object B is travelling the fastest.
(ii) No, all three objects do not meet at any point on the road.
(iii) When B passes A at point N (at 1.2 hours), C is at a distance of 8 km from the origin O.
(iv) B passes C at 0.7 hours. During this time B covers distance = 6 km.
Sponsor Area
The speed-time graph for a car is shown is Fig. 
(a) Find how far does the car travel in the first 4 seconds. Shade the area on the graph that represents the distance travelled by the car during the period.
(b) Which part of the graph represents uniform motion of the car?
(a)
![]()

State which of the following situations are possible and give an example of each of these:
(a) a body moving with constant acceleration but with zero velocity.
(b) a body moving in a certain direction with an acceleration in the perpendicular direction.
(a) Even when a body's velocity is zero a body can have acceleration.
For example, when a body is thrown up, at it's highest point veocity is zero. But, the acceleration of the body is equal to acceleration due to gravity.
(b) It is possible to have acceleration in the perpendicular direction for a body moving in a certain direction.
For example, an aeroplane moving horizontally is acted upon by acceleration due to gravity that acts vertically downwards.
Define the terms rest and motion. Give one example for each.
E.g. A table lying in a room is at rest with respect to the walls of the room.
Motion: A body is said to be in motion if it changes its position with respect to its surroundings.
E.g., A car running on the road is in motion with respect to the lamp posts, trees or bus stop on the roadside
Give one example each for directly and indirectly perceivable motions.
(i) Directly perceivable motion: Motion of vehicles moving on a road.
(ii) Indirectly perceivable motion: We perceive the motion of air indirectly by observing the movement of dust, leaves and branches of trees.
Show that rest and motion are relative terms.
Rest and motion are relative terms. this can be illustrated below using the following explanation.
Let's consider for example, a passenger sitting in a moving train. The passenger is at rest relative to other passenger of his compartment. But, the passenger is in motion relative to the outside trees, lamp posts, railway stations, etc.
So, we can see that rest and motion are in respect to relativity.
Describe the various types of motions observed in bodies.
Various types of motion as observed in bodies are:
1. Translatory motion: When a body moves as a whole along a straight or curved path, it is said to be in translatory motion.
Translatory motion is again of two types:
(i) Rectilinear motion: Here a body moves as a whole along a straight path.
For example, a train moving on straight rails has translatory rectilinear motion.
(ii) Curvilinear motion: In this case a body moves as a whole along a curved path.
For example, motion of a bicycle taking a turn along a curved path.
2. Rotatory motion: When a body rotates about a fixed point or axis, it exhibits a rotatory motion.
For example, motion of a flywheel about a shaft.
3. Vibratory or oscillatory motion: When a body moves to and fro about a mean position, the motion is said to be vibratory or oscillatory motion.
For example, the motion of the pendulum of a wall-clock.
4. Complex motion: When the motion of a body may be a combination of more than one types of motion, it is said to be a complex motion.
For example, a ball rolling down an inclined plane has both translatory and rotatory motions.
What is meant by a point object? Give some examples.
Whenever the size of the object is much smaller than the distance it moves in a given time interval, the size of the object can be neglected. The objet can be regraded as point object in such cases.
Examples:
(i) A car covering a distance of 10 km can be treated as a point object.
(ii) Earth can be regarded as a point object for studying its motion around the Sun.
How can we specify the position of an object?
The position of an object can be specified by choosing:
(i) a fixed point called ‘origin’ or reference point, and
(ii) a fixed line passing through the origin, called reference axis.
So the position of an object can be fully described by knowing:
(i) its distance from origin O and
(ii) the angle θ which the line joining the origin O and the object makes with the reference axis.
In Fig. the position of an object located at point P is 6 m from the origin and 30° north of east.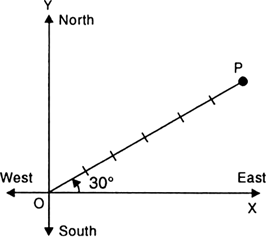
Fig. To specify the position of an object (Scale: 1 cm = 1m).
What are scalar quantities? Give examples.
Physical quantities which require only magnitude and not the direction for their complete description of motion are called ‘scalars’ or ‘scalar quantities’.
For example, distance, speed, time, area, etc. are some of the scalar quantities.
What are vector quantities? Give examples.
Physical quantities which need both magnitude and direction for their complete description of motion are called ‘vectors’ or ‘vector quantities’.
Some examples of vector quantities are displacement, velocity, force, etc.
Classify the following as scalar and vector quantities:
Temperature, mass, volume, speed, displacement, time, distance, velocity, electric charge, acceleration, force, momentum, density, work, weight, energy.
Scalar quantities: Temperature, mass, volume, speed, time, distance, electric charge, density, work and energy.
Vector quantities: Displacement, velocity, acceleration, force, momentum and weight.
What is meant by motion in a straight line ? Give some examples of such a motion.
When the position of a body changes with time, the body is said to be moving in a straight line.
Examples of motion in a straight line or rectilinear motion are:
(i) A bus moving on a straight road,
(ii) A train moving on a straight track,
(iii) A runner running along a straight track,
(iv) A ball moving along a straight path, and
(v) An object falling vertically downwards towards the surface of the earth.
With the help of a suitable example, explain the terms distance and displacement.
In Fig. 8.2, suppose a body moves from position A to B through C.
Then, distance travelled = AC + BC
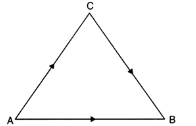
Fig. 8.2
Distance:
i) It is the length of the actual path travelled by a body between its initial and final positions.
ii) Distance is a scalar quantity because it has only magnitude and no direction.
iii) Distance covered is always positive or zero.
iv) Distance describes the total distance moved by an object.
Displacement:
i) The change in the position of an object in a given direction is known as displacement.
ii) It is the shortest distance measured in the direction from the initial to the final position of the body.
iii) Displacement has both magnitude and direction, so it is a vector quantity.
iv) Displacement may be positive, negative or zero.
v) Displacement is used to locate the final position of an object with reference to its initial position at a given time.
vi) The magnitude of displacement is always less than or equal to the distance travelled.
Give some points of differences between distance and displacement.
Differences between distance and displacement are:
|
Distance |
Displacement |
|
1. Distance is the length of the actual path traversed by a body, irrespective of its direction of motion. |
1. Displacement is the shortest distance between the initial and final positions of a body in a given direction. |
|
2. Distance between two given points may be same or different for different paths chosen. |
2. Displacement between two given points is always same. |
|
3. It is a scalar quantity. |
3. It is a vector quantity. |
|
4. Distance covered is always positive. |
4. Displacement covered may be positive, negative or zero. |
An object has moved through a distance, can it have zero displacement? If yes, support your answer with an example.
Yes. Suppose a person throws a ball upwards through height h and catches back
the ball.
Then,
Distance covered by the ball = h + h = 2h
Displacement of the ball = 0.
A farmer moves along the boundary of a square field of side 10 m in 40 s. What will be the magnitude of displacement of the farmer at the end of 2 minutes 20 seconds?
If the farmer starts from point A, then at the end of 2 minutes and 20 seconds (= 140 seconds), he will reach the diagonally opposite corner C.
The magnitude of displacement of the farmer is: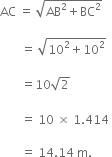
Which of the following is true for displacement?
(a) It can not be zero.
(b) Its magnitude is greater than the distance travelled by the object.
a) Statement is false. Displacement can be zero. If a body starts from a point and then comes back to the same point through the same path, displacement is zero. 
b) The magnitude of the displacement is always less than or equal to the distance travelled by the object.
A particle moves from a point P directly towards another point Q which is at a distance of 10 cm from P. It then comes back to P directly. Calculate:
(i) the total distance travelled; and
(ii) the displacement of the particle.
Given,
Distance between points P and Q = 10 cm
(i) Total distance travelled = PQ + QP
= (10 + 10) cm
= 20 cm.
(ii) Displacement of the particle will be zero, because the particle comes back to the initial position. That is, the initial and final position is same.
A body thrown in the vertically upward direction rises upto a height h and comes back to the position of start.
Calculate:
(i) the total distance travelled by the body; and
(ii) the displacement of the body.
Given, a body thrown vertically upward comes back to it's position of start. The body rise upto a height 'h' when thrown vertically up.
(i) The total distance travelled = h + h = 2h.
(ii) The displacement is zero, because the initial and final positions coincide.
In a long distance race, the athletes were expected to take four rounds of the track such that the line of finish was same as the line of start. Suppose the length of the track was 200 m.
(a) What is the total distance to be covered by the athletes ?
(b) What is the displacement of the athletes when they touch the finish line ?
(c) Is the motion of the athletes uniform or non-uniform ?
(d) Is the displacement of an athlete and the distance moved by him at the end of the race equal ?
Given,
Length of the track = 200 m
Expected rounds athlete are supposed to take = 4
(a) Total distance covered by each athlete = 4 × 200 = 800 m.
(b) As the line of finish is the same as the line of start, so displacement of each athlete = 0.
(c) Motion of the athletes is non-uniform as the speed of the athlete will be changing at each point.
(d) From parts (a) and (b), the distance and displacement of an athlete are not equal at the end of the race.
A particle moves in a circle with O as centre and AO = OB = 5 cm, as radius It starts from A. Calculate:
(i) the distance covered; and
(ii) the displacement, when it reaches B.
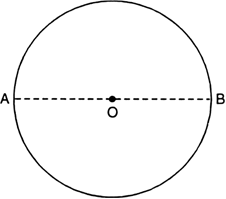
i) The distance covered,
(ii) The displacement = 2 × OB = 2 × 5 = 10 cm, along AB.
A person travels a distance of 1.5 m towards east, then 2.0 m towards south and finally 4.5 m towards east. Find:
(i) the total distance travelled, and
(ii) the total displacement.
Given, a person travels 1.5 m towards east, then 2.0 m towards south and then 4.5 m towards east. 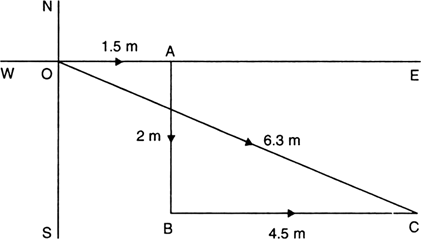
The displacement of 1 m by 1 cm length of a line is rep
The various displacements can be represented as follows: 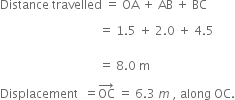
A person moves on a semicircular track of radius 42 m during a morning walk. He starts at one end of the track and reaches the other end. Find the
i) distance covered and
ii) the displacement of the person.
Given,
Radius of the semicircular track, r = 42 m
i) Distance covered is equal to the circumference of the semicircular track = pi * r
= 3.14 *42
= 131.8 m
= 132 m
ii) Displacement of the person = diameter of the semicircle = (42+ 42) = 84 m
A body travels a distance of 8 m from A to B, then moves a distance of 6 m at right angles to AB. What is the total distance travelled ? Find the magnitude of resultant displacement.
Distance travelled from A to B = 8 m
Distance travelled at right angles to AB = 6m
So, total distance covered = 8+6 = 14 m
Displacement = shortest distance covered by the body in any given time.
Therefore, Displacement =
A body moves towards east by a distance of 3 km and turns towards north and moves a distance of 4 km. What is the magnitude of displacement of the body?
Given,
Distance travelled in east direction = 3 km
Towards north = 4 km
The magnitude of the displacement would be the resultant BC.
Therefore, using Pythagoras theorem,
That is, 5 km is the magnitude of displacement.
What is meant by uniform motion ? Give an example.
When an object covers equal distances in equal intervals of time, however small the time interval may be, then the motion of the object is said to be uniform motion.
Consider for example, a bus moves 10 km in the first 15 minutes, 10 km in second 15 minutes, 10 km in third 15 minutes and so on.
Then one can say that the bus is in uniform motion.
What is non-uniform motion? Give some examples.
When an object covers unequal distances in equal intervals of time, the object is said to be in non-uniform motion.
the motions that we see in our daily life are usually examples of non- uniform motion.
For example, if we drop a ball from the roof of a building, we will note that the ball covers 4.9 m in the 1st second, 14.7 m in the 2nd second, 24.5 m in the 3rd second, and so on.
Here, the ball covers increasingly larger distances in successive seconds as it falls down.
Thus, the motion of a freely falling body is non-uniform.
Examples of non-uniform motion are:
(i) A stone dropped from the top of a building.
(ii) A ball thrown vertically upwards.
(iii) The motion of a train as it leaves the station.
(iv) The motion of a bus as it approaches a bus-stop.
(v) The motion of a ball rolling down an inclined plane.
Define the term speed. What are its various units? Is it a scalar or vector quantity?
Speed is defined as the distance travelled by a body per unit time.
Thus,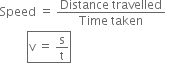
The SI unit of speed is ms-1 whenever the distance covered by body is expressed in metre and time in second.
A smaller unit of speed is cm s-1.
A larger unit of speed is km h-1.
Speed is a scalar quantity because it has only magnitude and no direction.
The speed of a body tells us how fast or how slow the body is moving. But it does not give the direction of motion.
Define uniform and non-uniform speeds.
Uniform speed:
When the speed of an object remains constant with time, that is it does not change in regular intervals of time, the speed is said to be uniform.
That, is if an object covers equal distances in equal intervals of time, the body is moving with a unifrom speed.
E.g., A cyclist is covering 5 km uniformly every 1 hour.
Non-uniform speed:
A body is said to be moving with non-uniform speed when an object covers unequal distances in equal inervals of time.
E.g., A soccer player moving in the football ground.
Define the term average speed.
Average speed is the total distance travelled by a body, divided by the total time taken to cover that distance. Thus,
Average speed = .
Define the term velocity. What is its SI unit ? Is it a scalar or vector quantity?
Velocity is a physical quantity that gives both the speed and direction of motion of the body.
Defintion: Velocity of a body is defined as the displacement produced per unit time. Velocity is also defined as the speed of a body in a given direction.
If s is the distance travelled by a body in a given direction and t is the time taken to travel that distance, then the velocity v is given by,
Velocity = displacement / time = s / t
Velocity is a vector quantity because it requires both magnitude and direction of a body.
When is a body said to have
(i) uniform velocity and
(ii) variable velocity ?
(i) Uniform velocity:
If a body covers equal distances in equal intervals of time in a given direction, the body is moving with a ‘uniform velocity’. The velocity of the body does not change with time. So in uniform velocity, a body moves with uniform speed in a given direction.
For example, light travels with a uniform velocity of 3×10 m/s through vacuum.
(ii) Variable velocity:
When a body travels unequal distances in equal intervals of time, such that its direction changes, or both change, velocity is said to be ‘variable velocity’.
For example, a bus turning at a junction has variable velocity.
Define average velocity when the velocity of a body changes at a nonuniform rate and a uniform rate.
Average velocity:
When the velocity of a body changes at a non-uniform rate, its average velocity is defined as the net displacement covered divided by the total time taken.![]()
When the velocity of a body changes at a uniform rate, then the average velocity is given by the arithmetic mean of initial velocity and final velocity for a given period of time.
![]()
If u is the initial velocity and v is the final velocity, then the average velocity vav is given by,
![]()
Give some points of differences between speed and velocity.
Difference between speed and velocity:
|
Speed |
Velocity |
|
1. Speed is the distance traversed by a body per unit time in any direction. |
1. Velocity is the distance traversed by a body in a given direction. |
|
2. It is a scalar quantity. |
2. It is a vector quantity. |
|
3. It is always positive or zero but never negative. |
3. It may be positive, negative or zero. |
Under what condition is the magnitude of average velocity of an object equal to its average speed?
When an object moves along a straight line in the same direction, its total path length is equal to the magnitude of displacement. Hence, its average speed is equal to the magnitude of average velocity.
What does the odometer of an automobile measure?
The odometer of an automobile measures the distance moved by it.
What does the path of an object look like when it is in uniform motion?
When an object is in uniform motion, the body follows a straight line path.
During an experiment, a signal from a spaceship reached the ground station in five minutes. What was the distance of the spaceship from the ground station ? The signal travels at the speed of light, that is, 3 × 108 ms-1.
Here we have,
time, t = 5 minutes = 300 s,
Speed with which the signal is travelling, v = 3 × 108 ms-1
Now, using the formula, we get
Distance of spaceship, s = vt
= 3 × 108 × 300
= 9 × 1010 m.
The velocity of a car is 18 m/s. Express the velocity in km/h.
Now, the velocity of the car in km/hr is given by,
Arrange the following speeds in increasing order:
(i) Bicycle moving with a speed of 18 km/h.
(ii) A fast runner running with a speed of 7 m/s.
(iii) A car moving with a speed of 2000 m/min.
To compare the various speeds, we first express them in the same units: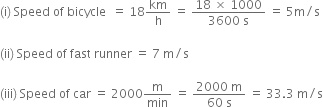
Clearly, Speed of bicycle < Speed of fast runner < Speed of car.
Light travels with a speed of 3 × 108 m/s. How long does the light take to reach earth from the sun which is 1.5 × 1011 m away?
Therefore, time taken to reach Earth from sun is,
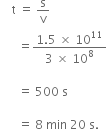
A 100 m long train crosses a 300 m long bridge at a speed of 90 km/hour. How much time will it take to cross the bridge completely?
Length of the train = 100 m
Length of the bridge = 300 m
Distance covered in crossing the bridge completely is, 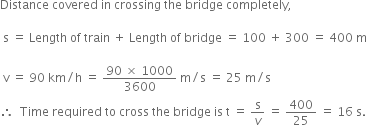
Usha swims in a 90 m pool. She covers 180 m in one minute by swimming from one end to the other and back along a straight path. Find the average speed and average velocity of Usha.
Total distance covered by Usha in 1 min = 180 m.
Displacement of Usha in 1 min = 0 
A cheetah is the fastest land animal and can achieve a peak velocity of 100 km/h upto distances less than 500 m. If a cheetah spots his prey at a distance of 100 m, what is the minimum time it will take to get its prey, if the average velocity attained by it is 90 km/h.
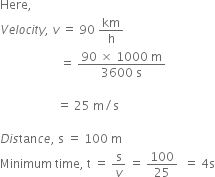
So, the minimum time the cheetah will get it's prey is 4 seconds.
All buses and cars these days are fitted with a speedometer, which shows the velocity of the vehicle. A device called odometer records the distance moved by the vehicle. If the reading on the odometer of a vehicle in the beginning of a trip and after 40 minutes were 1048 km and 1096 km respectively, calculate its average velocity. Will the reading on the speedometer show this velocity when the vehicle is moving? Support your answer with reason.
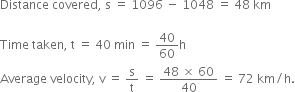
Speedometer will not show this average velocity because it reads instantaueous velocity which may be different from the average velocity.
The average time taken by a normal person to react to an emergency is one fifteenth of a second and is called the ‘reaction time’. If a bus is moving with a velocity of 60 km/h and its driver sees a child running across the road, how much distance would the bus had moved before he could press the brakes ? The reaction time of the people increases when they are intoxicated. How much distance had the bus moved if the reaction time of the driver were ½ s under the influence of alcohol?
Given,
Velocity of the moving bus = 60 km/hr
Distance ravelled by the bus before brakes are applied = ?
During the time of reaction, the velocity remains constant. 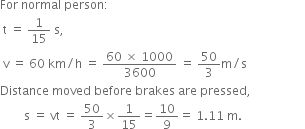
When the driver is under the influence of alcohol, 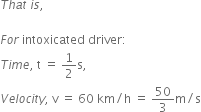
Distance moved before brakes are pressed,
![]()
That is the bus will be travel a lesser distance when the driver is under the influence of alcohol.
A girl had designed a clap switch for a science exhibition that enabled her to switch on or off an alarm just with clapping of hands. While testing her device in a hall, she noticed that once the alarm has sounded, it followed with another one due to echo of the clap, that is, the sound reflected by the walls. She recorded the two soundings of alarm with her tape recorder and found out that time difference. Distance travelled by sound in going towards the walls and on being reflected, in between them is 0.1 s. If the distance of the walls be 15 m, calculate the speed of sound.
Distance travelled by sound in going towards the walls and on being reflected, s = 15+15 = 30 m![<pre>uncaught exception: <b>Http Error #404</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php line 61<br />#0 [internal function]: com_wiris_plugin_impl_HttpImpl_0(Object(com_wiris_plugin_impl_HttpImpl), NULL, 'http://www.wiri...', 'Http Error #404')
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('com_wiris_plugi...', Array)
#2 [internal function]: _hx_lambda->execute('Http Error #404')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(532): call_user_func_array(Array, Array)
#4 [internal function]: haxe_Http_5(true, Object(com_wiris_plugin_impl_HttpImpl), Object(com_wiris_plugin_impl_HttpImpl), Array, Object(haxe_io_BytesOutput), true, 'Http Error #404')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('haxe_Http_5', Array)
#6 [internal function]: _hx_lambda->execute('Http Error #404')
#7 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(27): call_user_func_array(Array, Array)
#8 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(444): com_wiris_plugin_impl_HttpImpl->onError('Http Error #404')
#9 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(458): haxe_Http->customRequest(true, Object(haxe_io_BytesOutput), NULL, NULL)
#10 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(40): haxe_Http->request(true)
#11 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(80): com_wiris_plugin_impl_HttpImpl->request(true)
#12 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#13 {main}</pre>](/application/zrc/images/qvar/SCEN9014900-3.png)
A car travels a certain distance with a speed of 50 km/h and returns with a speed of 40 km/h. Calculate the average speed for the whole journey.
Let the car travel one way distance of x km.
A train moves with a speed of 30 km/h in the first 15 minutes, with another speed of 40 km/h in the next 15 minutes and then with a speed of 60 km/h in the last 30 minutes. Calculate the average speed of the train for this journey.
Distance covered by the train in the first 15 minutes is, 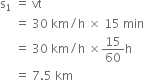

So, average speed of the train for this journey = 47.5 km/hr
A train is moving with a speed of 72 km/h. What is its speed in m/s?
Given,
Velocity = 72 km/hr
So,
Velocity in m/s will be given by,
v =
A train 40 m long passes over a bridge 200 m long at a speed of 36 km/h. How long will it take to pass completely over the bridge?
Length of the train = 40 m = 0.04 km
Length of the bridge = 200 m = 0.2 km
Speed of the train = 36 km/hr
The total time taken by the train to completely pass over the bridge is given by time for the front of the train to travel 200 m at 36 km/hr + time for the back of train to travel 40 m at a speed of 36 km/hr.
Therefore,
Total time taken =
A car covers the first half of the distance between two places at a speed of 40 km/h and the second half at 60 km/h. What is the average speed of the car?
Let, the total distance covered the car be 'd'.
Given,
Speed in the first half = 40 km/hr
Speed in the second half of distance = 60 km/hr
Let the time taken by the car in the first half = t1
Therefore,
Time,
Time taken by car in the second half, t2 =
Now, average speed =
A car travels 270 km in 4.5 hours. Calculate:
(i) its speed;
(ii) how far will it go in 7 hours at this speed; and
(iii) how long will it take to travel 300 km at this speed.
Given,
Distance travelled by the car = 270 km
Total time for travel = 4.5 hours
i) Speed of the car, v =
=
ii) Speed = 60 km/hr
Time taken = 7 hours
Distance travelled =
= 420 km
(iii) Speed = 60 km/hr
Distance to be travelled = 300 km
Time taken =
=
A car goes from a town A to another town B with a speed of 40 km/h and returns back to the town A with a speed of 60 km/h. Calculate the average speed during the whole journey.
Let the total distance travelled to and fro be d
Speed while ging from town A to town B = 40 km/hr
Speed while coming back from town B to town A = 60 km/hr
Time taken to go to town B ,t1 =
t1 =
Time taken to return to town A, t2 =
Average speed =
Define acceleration. Is it a scalar or a vector quantity?
Acceleration is defined as the rate of change of velocity with time.
When the motion is non-uniform, the velocity of a body changes with time. It has different velocities at different instants of time and at different points of it's path.
If the velocity of a body changes from u to v in time t, then
Acceleration is avector quantity and has both magnitude and direction.
When is the acceleration of a body positive?
When the acceleration of the motion is in the same direction as the velocity, acceleration is positive.
E.g., Acceleration of a bus when it just leaves the bus-stop.
What do you mean by the term retardation? Give two examples of such a motion.
When the velocity of a body decreases, its acceleration is negative. Negative acceleration is called ‘retardation’ or ‘deceleration’.
For example, when a stone is thrown upwards, it is under retardation.
Similarly, when a bus approaches a bus-stop, its motion gets retarded.
In both the cases mentioned above the acceleration decreases.
When do you say a body is in
(i) uniform acceleration, and
(ii) variable acceleration?
(i) Uniform acceleration:
When an object travels in a straight line and its velocity changes by equal amounts in equal intervals of time, the object is said to be in ‘uniform acceleration’.
For example, a body falling freely to the ground has a uniform acceleration of 9.8 m/s2 as its velocity increases by 9.8 m/s after every one second.
(ii) Variable acceleration:
When the velocity of an object changes by unequal amounts in equal intervals of time, the object is said to have ‘variable acceleration’.
For example, if the speed of a car travelling along a straight road increases by unequal amounts, then the car is moving with non-uniform acceleration.
Give two examples of uniformly accelerated motions.
Examples of uniformly accelerated motions are:
(i) An object moving with uniform speed along a circular path, has uniform acceleration. In this case the velocity of the object changes continuously due to change in its direction at each point.
(ii) The motion of a ball rolling down an inclined plane is uniformly accelerated.
A bus decreases its speed from 80 km/h to 60 km/h in 5 seconds. Find the acceleration of the bus.

So, the bus is decelerating at a rate of -1.11 m/s2.
What are the equations of motion for a body in linear motion?
When an object moves along a straight line with uniform acceleration, it is possible to relate its velocity, acceleration during motion and the distance covered by it in a certain time interval by a set of equations known as the equations of motion.
A body starts initially with a velocity ‘u’ and is accelerated at constant rate ‘a’. Find an expression for final velocity after time ‘t’.
Or
Establish the relation: v = u + at.
First equation of motion:
Let a body start with initial velocity 'u' and after time t, its velocity becomes v due to uniform acceleration a.
From the definition of acceleration, 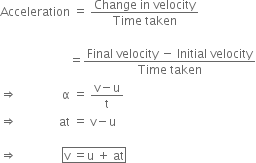
Deduce the expression for the distance travelled by a body moving with uniform acceleration, in a given time.
Second equation of motion gives us the distance travelled by a body moving with uniform acceleration, in a given time.
Suppose the body starts with initial velocity u and due to uniform acceleration a, its final velocity becomes v after time t.
Then,
Average velocity is given by, 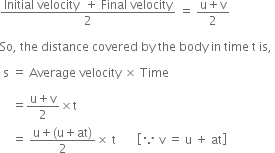

Establish the relation v 2 – u2 = 2as, where ‘u’ is the initial velocity, ‘v’ the final velocity, ‘a’ the uniform acceleration and ‘s’ is the distance covered by the body.
Third equation of motion:
Let a body start with initial velocity u. After covering distance 's' under uniform acceleration 'a', its velocity becomes 'v' in 't' seconds.
Then, ![]()
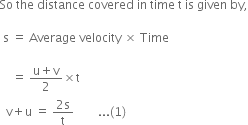
Now, using the first equation of motion:
v = u + at ![]() v - u = at ... (2)
v - u = at ... (2)
Multiplying equations (i) and (ii), we get
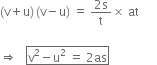
A trolley while going down an inclined plane has an acceleration of 2 m/s2. What will be its velocity in 3 seconds after the start?
![<pre>uncaught exception: <b>Http Error #404</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php line 61<br />#0 [internal function]: com_wiris_plugin_impl_HttpImpl_0(Object(com_wiris_plugin_impl_HttpImpl), NULL, 'http://www.wiri...', 'Http Error #404')
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('com_wiris_plugi...', Array)
#2 [internal function]: _hx_lambda->execute('Http Error #404')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(532): call_user_func_array(Array, Array)
#4 [internal function]: haxe_Http_5(true, Object(com_wiris_plugin_impl_HttpImpl), Object(com_wiris_plugin_impl_HttpImpl), Array, Object(haxe_io_BytesOutput), true, 'Http Error #404')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('haxe_Http_5', Array)
#6 [internal function]: _hx_lambda->execute('Http Error #404')
#7 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(27): call_user_func_array(Array, Array)
#8 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(444): com_wiris_plugin_impl_HttpImpl->onError('Http Error #404')
#9 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(458): haxe_Http->customRequest(true, Object(haxe_io_BytesOutput), NULL, NULL)
#10 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(40): haxe_Http->request(true)
#11 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(80): com_wiris_plugin_impl_HttpImpl->request(true)
#12 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#13 {main}</pre>](/application/zrc/images/qvar/SCEN9014925-3.png)
Thus, velocity of the trolley after 3 sec is 6 m/s.
A body starting from rest travels with uniform acceleration. If it travels 100 m in 5 s, what is the value of acceleration?
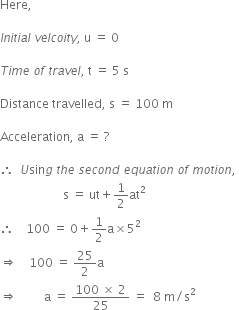
Therefore, the body is accelerating at the rate of 8 m/s2.
A train is travelling at a speed of 90 km/h. The brakes are applied so as to produce a uniform acceleration of - 0.5 m/s2. Find how far the train goes before it stops?

Therefore, distance travelled by the train before it stops = 625 m
What are the uses of graphical study of motion?
Graphical representation of motion is useful to study the nature of motion of bodies. In this type of representation, time is plotted along X-axis while distance or velocity is plotted along Y-axis.
Graphs give more detailed information about the nature of motion than when motion is expressed in a tabular form.
The uses of graphical representaion of motion are:
(i) From distance-time graph the position of the body at any instant of time can be determined.
(ii) Distance covered by the body during particular interval of time can be seen from the graph.
(iii) The velocity of the body at any instant of time can be determined.
(iv) By simply looking at the graph, one can tell whether motion is uniform or not.
(v) Slope of velocity-time graph gives the acceleration of the body.
(vi) Graphs are very useful for comparing the motions of two moving bodies. Distance-time graphs easily tell when and where one body crosses the other body.
What is distance-time graph of a body? Draw distance-time graphs for,
(i) a stationary body,
(ii) a body moving with uniform velocity, and
(iii) a body moving with variable velocity.
Distance-time graph:
It is a graph obtained by plotting distance travelled along Y-axis and time taken along X-axis.
(i) Distance-time graph for stationary body:
The position of a stationary body does not change with time. So distance-time graph for a stationary body is a straight line parallel to time axis, as shown in Fig. 8.7 (a).
(ii) Distance-time graph for uniform velocity:
For a body moving with uniform velocity, the distance travelled is proportional to the time taken. So distance-time graph is a straight line inclined to the time axis, as shown in Fig. 8.7 (b).
(iii) Distance-time graph for variable velocity:
When a body moves with variable velocity, it covers unequal distances in equal intervals of time. So the distance-time graph is not a straight line but it is a curve, as shown in Fig. 8.7 (c). 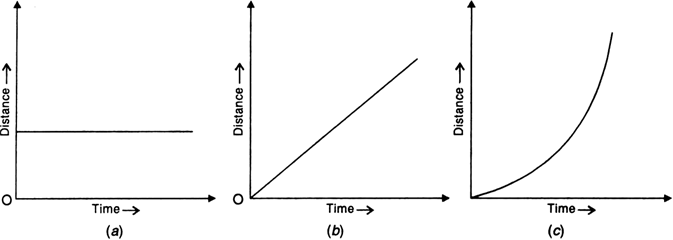
Mention the uses of a distance-time graph.
Distance-time graph can be useful in the following ways:
(i) It tells the position of the body at any instant of time.
(ii) The distance covered by the body during a particular interval of time can be seen from the graph.
(iii) The velocity of the body at any instant of time can be determined.
Show that the slope of distance-time graph gives velocity of the body.
Consider the figure given below: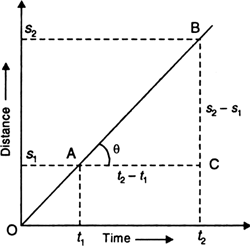
This is a distance-time graph for a body moving with uniform velocity.
Clearly, it covers distances S1 and s2 at times t1 and t2 respectively. 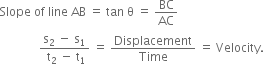
Hence, the slope of the distance-time graph gives velocity of the body.
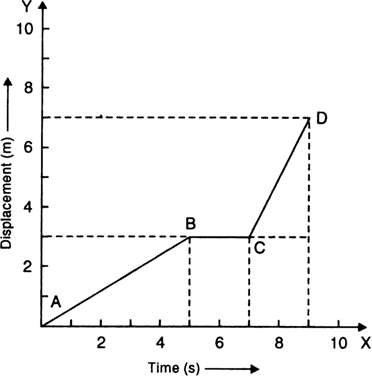
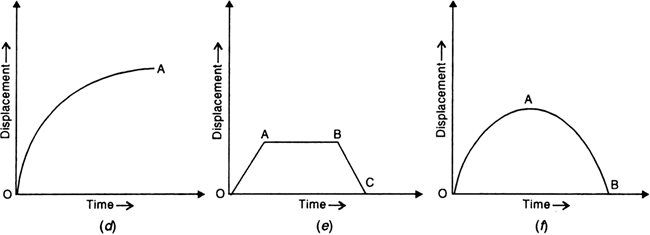
What conclusions do you draw about the motion of a body from the following displacement-time graphs: 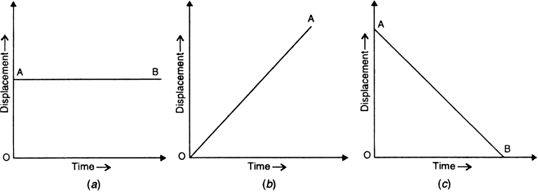
(a) From A to B, the body is at rest.
(b) From O to A, the body is moving with a uniform velocity (positive).
(c) From A to B, the body is moving with a uniform negative velocity.
(d) From O to A, the body has positive variable velocity.
(e) From O to A, the body has uniform positive velocity, from A to B the body has zero velocity and from B to C, the body has uniform negative velocity.
(f) From O to A, the body has variable positive velocity and from A to B, the body has variable negative velocity.
The following table shows the distance travelled by a car, moving with uniform acceleration, in time intervals of two seconds. Draw a distance-time graph for the motion of the car. Indicate whether the motion is uniform or not. ![]()
The distance-time graph for the motion of the car is shown in Fig.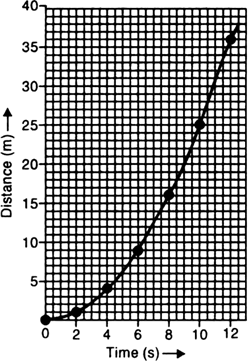
The motion of the car is non-uniform because it is a curved line.
What is velocity-time graph of a body? Draw velocity-time graphs for
(i) a body moving with uniform velocity,
(ii) a body moving with uniform acceleration, and
(iii) a body moving with variable acceleration.
Velocity-time graph
It is the graph obtained by plotting velocity of the body along Y-axis and time along X-axis.
(i) Velocity-time graph for uniform velocity. For a body moving with a constant velocity, the velocity-time graph is a straight line parallel to the time-axis, as shown in Fig. (a).
(ii) Velocity-time graph for uniform acceleration. For a body in uniform acceleration, the increase in velocity is proportional to the time taken. So velocity-time graph is a straight line inclined to the time-axis, as shown in Fig. (b).
(iii) Velocity-time graph for variable acceleration. For a body having variable acceleration, the velocity increases by unequal amounts in equal intervals of time. So velocity-time graph is a curve, as shown in Fig. (c).
Mention the uses of a velocity-time graph.
The use of velocity-time graph are as follows:
(i) To determine the speed of a body at any instant of time.
(ii) To determine the acceleration of a body.
(iii) To determine the total distance travelled by a body in a given time-interval.
Show that the slope of velocity-time graph gives acceleration of the body.
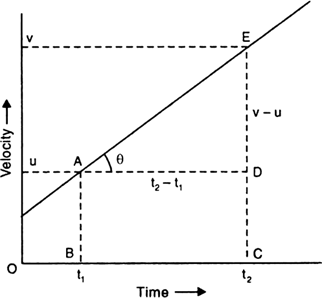
The fig. shows the velocity-time graph for a body in uniform acceleration.
Body has velocities u and v at times t1 and t2respectively.
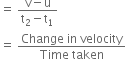
= Acceleration of the body
Hence, the slope of the velocity-time graph gives the acceleration of the body.
Draw velocity-time graph for a body moving with uniform velocity. Hence show that the area under the velocity-time graph gives the distance travelled by the body in a given time interval.
Consider the figure as below. 
Distance covered as area under the velocity-time graph.
In Fig., line PQ is the velocity-time graph of a body moving with a uniform velocity, OP = v.
Area of rectangle ABCD
= AD × AB = OP × AB
= v × (t2 – t1)
= Velocity x time
= Distance travelled in time interval (t2 – t1)
Hence, the area under the velocity-time graph gives the distance travelled by the body in the given time interval.
Draw a velocity-time graph for a body in uniform acceleration. Hence, show that the area under the velocity-time graph gives the distance travelled by the body in the given time interval.
Distance covered as area under the velocity-time graph. 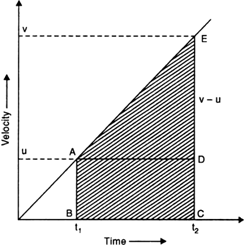
Fig. 8.14: Velocity-time graph for uniform acceleration.
The figure above shows the velocity-time graph for a body in uniform acceleration.
The graph is a straight line inclined to the time-axis.
The body has velocities u and v at times t1 and t2 respectively.
= Average velocity x Time interval
= Distance travelled in the time interval ![]()
Hence, the area under the velocity-time graph gives the distance travelled by the body in the given time interval.
What types of motions are represented by the following velocity-time graphs? 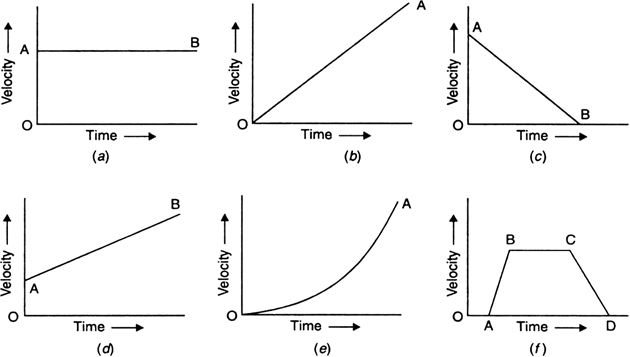
(a) Since the velocity-time graph is a straight line, the body has uniform velocity.
(b) The body has uniform acceleration and its initial velocity is zero because the lne starts from the origin.
(c) The body has some initial velocity and is under uniform retardation.
(d) The body has some initial velocity and uniform acceleration.
(e) The body has zero initial velocity and it has variable acceleration.
(f) The body is at rest from O to A, it has uniform acceleration from A to B, it has uniform velocity from B to C and from C to D, the body is under uniform retardation.
What types of motions are represented by the following velocity-time graphs? 
Fig. (a) represents the velocity-time graph for a body whose velocity is decreasing uniformly with time.
Fig. (b) represents the velocity-time graph of the oscillating motion of body with time.
What is the nature of the distance-time graphs for uniform and non-uniform motion of an object?
The distance-time graph for uniform motion is a straight line inclined with the time axis.
The distance-time graph is a curved line for non-uniform motion.
What can you say about the motion of an object whose distance-time graph is a straight line parallel to the time-axis?
The object is at rest, if the line is parallel to the time-axis.
What can you say about the motion of an object if its speed-time graph is a straight line parallel to the time-axis?
The object is moving with a uniform speed.
What is the quantity which is measured by the area occupied below velocity-time graph?
The area occupied below velocity - time graph is the distance covered by the body in the given time interval.
Derive the equations of motion for uniformly accelerated motion from velocity-time graph.
Equations of motion by graphical method:
Consider an object moving along a straight line with initial velocity 'u' and uniform acceleration a.
Suppose, it travels distance s in time t.
As shown in Fig. 8.19, its velocity-time graph is straight line. 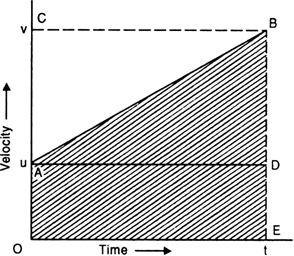
Here,
OA = ED = u
OC = EB = v and
OE = t = AD.
1. Equation for velocity-time relation.
Acceleration is given by slope of velocity-time graph AB
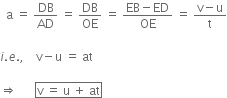
Hence, the first equation of motion is proved.
2. Equation for position-time relation:
From the first part, we have

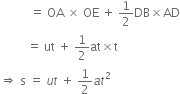
This proves the second equation of motion.
3. Equation for position-velocity relation:
The distance travelled by object in time t is,
s = Area of trapezium OABE
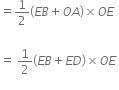
Acceleration, a = slope of velocity-time graph AB.
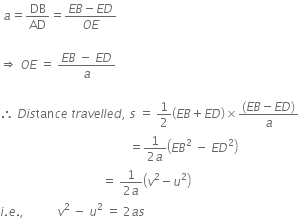
Hence, the third equation of motion is also proved.
A racing car has a uniform acceleration of 4 ms-2. What distance will it cover in 10 seconds after start?
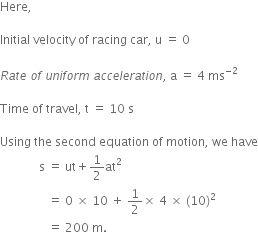
So, distance travelled by the car in 10 seconds = 200 m
Plot the distance-time graph of a body at rest (that is, not moving), at a distance of 100 m from the origin.
For a body at rest, distance-time graph is a straight line parallel to the time-axis.
the graph obtained is shown in the fig.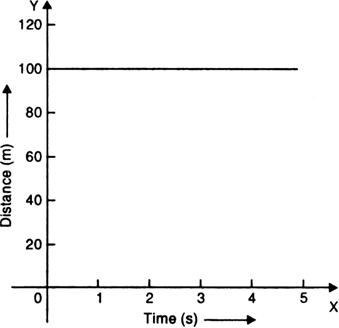
Discuss the graphs A, B and C shown in Fig. 8.21. Compare the total distance travelled and the displacements. Which graph represents a motion in which total displacement is zero?
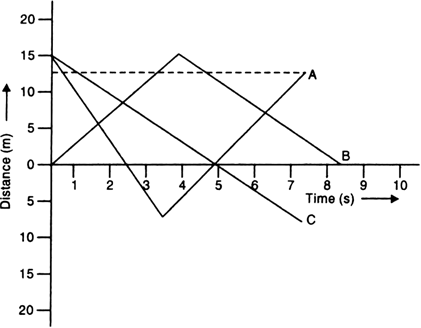

(i) In graph A,
Total distance travelled = 15 + 7.5 + 7.5 + 12.5
= 42.5 m
Graph B,
Total distance travelled = 15 + 15 = 30 m
Graph C,
Total distance travelled in graph C = 15 + 7.5 = 22.5 m.
(ii) Displacement is the shortest distance between the initial and final positions.
∴ Displacement in graph A = 12.5 – 15 = – 2.5 m.
Displacement in graph B = 0 – 0 = 0m. [ Because the object is returning back to the initial point]
Displacement in graph C = – 7.5 - 15 = – 22.5 m.
(iii) In graph B,
Before t = 4 s, the velocity is positive and after t = 4 sec, velocity is negative.
So the acceleration is negative at t = 4 s in graph B.
Plot distance-time graphs of bodies moving with uniform speeds of 4 m/s and 7 m/s. Compare the graphs.
For a body moving with a uniform speed of 4 m/s
For a body moving with a uniform speed of 7 m/s
The graphical representation for the objects moving with uniform speed is a straight line. 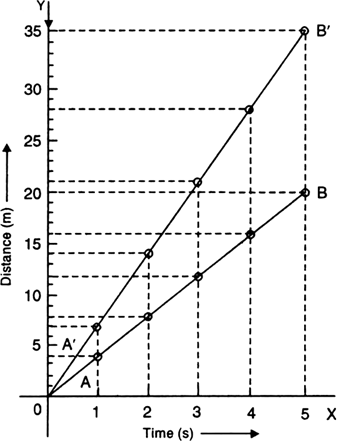
For the body moving with a uniform speed of 7 m/s, the distance-time graph is the straight line A'B'.
Clearly, slope of graph A'B' is more than that of graph AB.
In this figure shows the distance-time graphs of two objects A and B moving with uniform speeds. Which of the two objects is moving faster?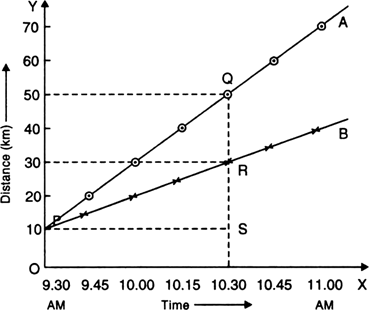
Given, distance-time graph of two objects A and B moving with uniform speed.
Thus we can see that distance-time graph for body A has greater slope.
Hence, object A is moving faster than body B.
The positions of a ball rolling down an inclined plane at the end of each second are given in the following table:
Plot a displacement-time graph for the motion of the ball. Indicate whether the motion is uniform or non-uniform.
The displacement-time graph for the motion of the ball is as shown in Fig. below.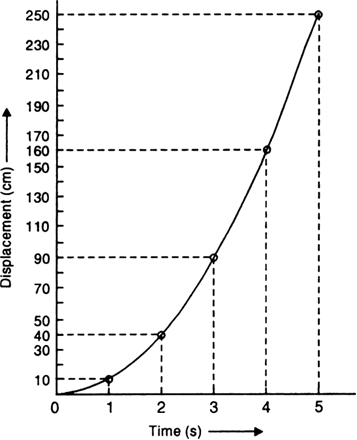
Fig. 8.25. Displacement-time graph for non-uniform motion.
The displacement-time graph is a curve, so motion of the ball is non-uniform.
Fgure 8.26 shows the distance-time graphs of two trains, which start moving simultaneously in the same direction. From the graphs, find:
(i) How much ahead of A is B when the motion starts?
(ii) What is the speed of B?
(iii) When and where will A catch B?
(iv) What is the difference between the speeds of A and B?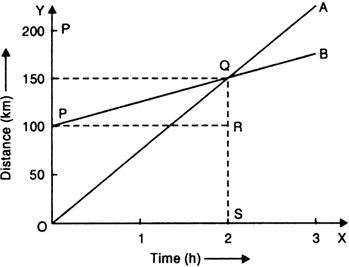
(i) When the motion started, B is ahead of A by distance OP = 100 km![]()
(iii) As it is clear from graphs, A will catch B at point Q, i.e., after 2 hours and at a distance of 150 km.
![]()
The following is the distance-time table of a moving car. 
(i) Use a graph-paper and plot the distance travelled by the car versus time.
(ii) When was the car travelling with the greatest speed ?
(iii) What is the average speed of the car?
(iv) What is the speed between 11.25 a.m. and 11.40 a.m.?
(v) During a part of the journey, the car was forced to slow down to 12 km/h. At what distance did this happen?
(i) The distance-time graph for the motion of the car is as shown in the figure below.
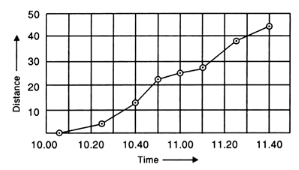
(ii) The car is travelling with maximum speed between 10.40 a.m. and 10.50 a.m.
During this time the distance-time graph has maximum slope.
Here
Speed of the car = ![]()
(iii) Average speed of car between 10.05 a.m. and 11.40 a.m.
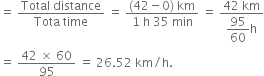
(iv) Speed between 11.25 a.m. and 11.40 a.m.
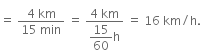
(v) Between 11.00 a.m. to 11.10 a.m., the car was forced to slow down to 12 km/h.
So, this happened at a distance of 26 km.
Plot speed-time graph of bodies moving with uniform speeds of 4 m/s and 7 m/s. Compare the graphs.
When a body is moving with a uniform speed, its speed-time graph is a straight line parallel to time-axis.
In Fig. below, the line AB represents the speed-time graph of a body moving with a uniform speed of 4 m/s, while line A'B' represents the speed-time graph of a body moving with uniform speed of 7 m/s.
The graph A 'B' is at larger distance from time-axis than the graph AB.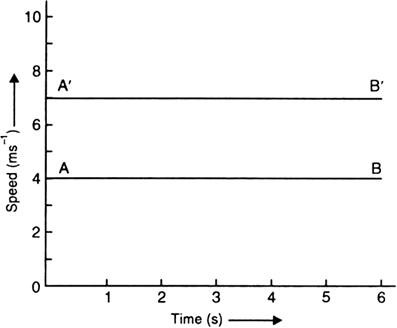
Speed-time graphs for uniform speeds of 4 m/s and 7 m/s.
Both figures are shows the speed-time graphs of two cars (a) and (b) respectively.
Using these graphs answer the following questions:
(i) What is the acceleration of the car (a) and car (b) in the first two hours, in the next two hours and in the last two hours?
(ii) What is the total distance travelled by the two cars?
(iii) What is the average speed of the two cars? 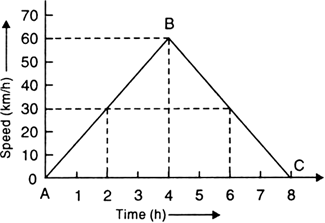
Fig. 8.29
i) Acceleration of car (a) in first two hours is given by,
![]()
Acceleration of car (A) in the next two hours is given by,
![]()
Acceleration of car (a) in the last two hours,
![]()
The negative accelerations means that the car is deccelerating.
ii) Total distance travelled by the car (a) in 8 hours is,
Area of ![]() =
= ![]()
= ![]()
iii) Average speed of the car (a) is,

A body moves from rest from a point A. It moves to another point B in 10 s, the motion being accelerated one and achieves a velocity 60 m/s at B. It then moves on to C with the uniform velocity for 20 s when it is immediately brought to rest. Draw a graph showing the complete motion and calculate the total distance travelled.
Given, a body from rest.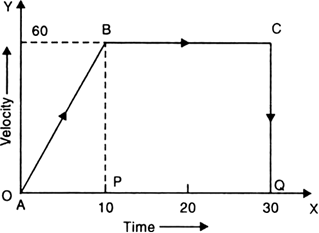
The above figure illustrates the motion of body at different points.
AB represents the accelerated part of motion.
BC represents the uniform motion.
At C, velocity of the body is abruptly made zero (point Q).
Distance travelled during the first 10 s is,
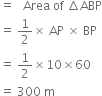
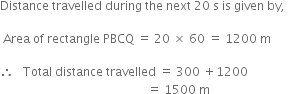
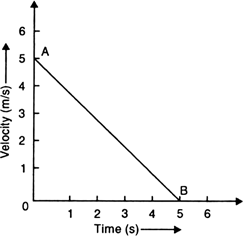
Plot the velocity-time graph of a body whose initial velocity is 5 m/s and is moving with a retardation of 1 m/s2. Calculate the distance covered by it.
AB is the velocity-time graph of a body.
Initial velocity of the body = 5 m/s
The body is moving with a retardation of 1 m/s2 as shown in Fig.
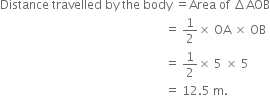
A car accelerates at a constant rate of change of velocity in 5 seconds from 10 m/s to 25 m/s on a highway. What is the acceleration and how far does the car go in this time-interval ? Give a graphical solution.
as shown in the fig. AB is the speed-time graph for the motion of the car.
A body moves with a velocity of 2 m/s for 5 s, then its velocity uniformly increases to 10 m/s in next 5 s. Thereafter its velocity begins to decrease at a uniform rate until it comes to rest after 10 s.
(a) Plot a velocity-time and distance-time graph for the motion of the body.
(b) Mark the portions of the graph to show when the motion of the body is uniform and when it is non-uniform.
(c) From the graph find the total distance moved by the body after 2 s and 12 s and in the last 10 s.
(a) Fig. 8.34 shows the velocity-time graph and Fig. 8.35 shows the distance-time graph for the motion of the body.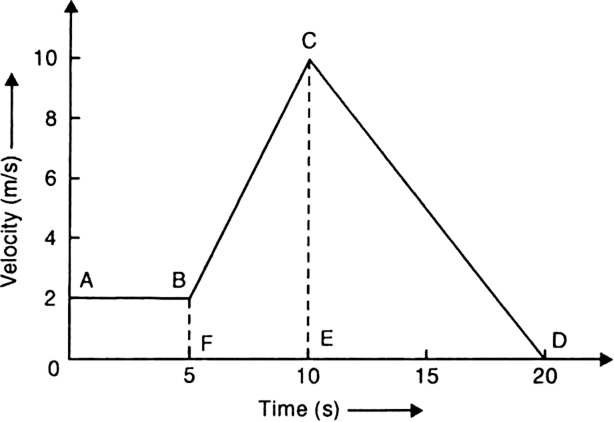
Fig. 8.34. Velocity-time graph.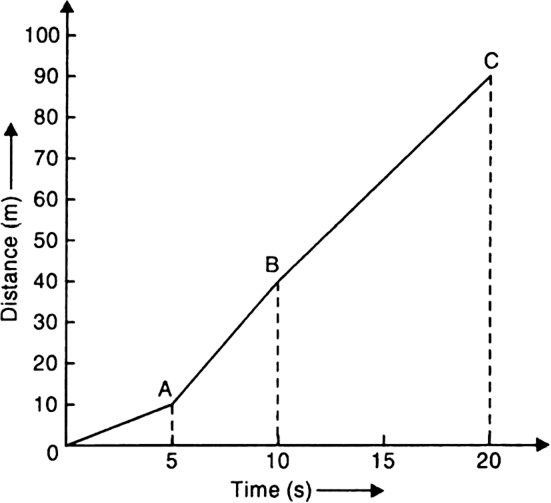
Fig. 8.35. Distance-time graph.
(b) From velocity-time, graph as shown in the fig., we note that the motion is uniform in portion AB and non-uniform in portions BC and CD.
(c) From distance-time graph, we observe the following:
Distance moved after 2 s = 4 m.
Distance moved after 12 s = 50 m.
Distance moved in last 10 s = 90 - 40= 50 m.
What is uniform circular motion? Is this motion accelerated or not? What is the direction of velocity at any point? Give an examples of uniform circular motion.
Uniform circular motion:
when a body moves with a uniform speed along a circular path, it is said to be in uniform circular motion.
The direction of velocity changes at every point but the magnitude of the body remains constant.
Therefore, unifrom circular motion is an example of accelerated motion.
The direction of velocity at any point of the circular path is along the tangent at that point as shown in Fig. below.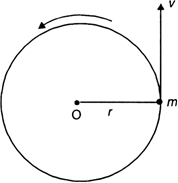
Examples of uniform circular motion:
(i) A cyclist moving along a circular track at constant speed.
(ii) Motion of the moon around the earth.
(iii) Motion of a satellite in circular orbit around the earth.
(iv) Motion of a stone being rotated at the end of a string.
Express the velocity of a body in uniform circular motion in terms of its time period T.
Suppose a body of mass m rotates in a circle of radius r with velocity v.
The rotaing body completes one revolution in time T.
Then,
![<pre>uncaught exception: <b>Http Error #502</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php line 61<br />#0 [internal function]: com_wiris_plugin_impl_HttpImpl_0(Object(com_wiris_plugin_impl_HttpImpl), NULL, 'http://www.wiri...', 'Http Error #502')
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('com_wiris_plugi...', Array)
#2 [internal function]: _hx_lambda->execute('Http Error #502')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(532): call_user_func_array(Array, Array)
#4 [internal function]: haxe_Http_5(true, Object(com_wiris_plugin_impl_HttpImpl), Object(com_wiris_plugin_impl_HttpImpl), Array, Object(haxe_io_BytesOutput), true, 'Http Error #502')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('haxe_Http_5', Array)
#6 [internal function]: _hx_lambda->execute('Http Error #502')
#7 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(27): call_user_func_array(Array, Array)
#8 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(444): com_wiris_plugin_impl_HttpImpl->onError('Http Error #502')
#9 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(458): haxe_Http->customRequest(true, Object(haxe_io_BytesOutput), NULL, NULL)
#10 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(40): haxe_Http->request(true)
#11 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(80): com_wiris_plugin_impl_HttpImpl->request(true)
#12 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#13 {main}</pre>](/application/zrc/images/qvar/SCEN9014977-3.png)
Define the terms angular displacement, angular velocity, time period and frequency in respect of uniform circular motion?
Angular displacement (θ) is the angle swept by the radius in a given time interval.
Mathematically, it is given by
![]()
Angular velocity (ω) is the angle swept out by the radius per unit time is called angular velocity.
![]()
Time period is the time taken for one complete revolution is called .
Frequency is the number of revolutions completed per unit time is called frequency (v).
![]()
Derive a relation between linear velocity and angular velocity?
Consider a particle moving with uniform angular velocity co along a circular path of radius r.
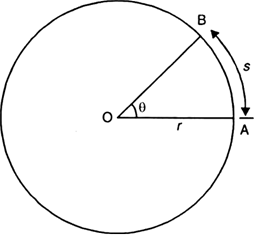
Suppose it moves from A to B to cover distance s along arc AB.
![]()

What is the angular speed of the second’s hand of a clock, assuming that it moves with a constant angular speed. If the length of the second’s hand is 4 cm, calculate the speed of the tip of the second’s hand.
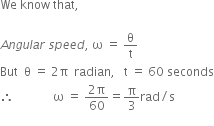
If the tyre of a car has a diameter of 0.8 m and the wheel has an angular velocity of 20 rad/s, what is the speed of the car in m/s?
Given that,
Diameter = 0.8 m.
Therefore, radius (r) = 0.4 m.
Angular velocity, ω = 20 rad/s
![]()
A circular cycle track has a circumference of 314 m with AB as one of its diameter. A cyclist travels from A to B along the circular path with a velocity of constant magnitude 15.7 m/s. Find:
(a) the distance moved by the cyclist.
(b) the displacement of the cyclist if AB represents north-south direction.
(c) the average velocity of the cyclist.
Given, a circular track of circumference 314 m. 


A circular track has a circumference of 3140 m with AB as one of its diameter. A scooterist moves from A to B along the circular path with a uniform speed of 10 m/s. Find
(a) distance covered by the scooterist,
(b) displacement of the scooterist, and
(c) time taken by the scooterist in reaching from A to B.
Circumference of the circular track = 3140 m

Can an object be at rest as well as in motion at the same time?
Rest and motion are relative terms. So, an object may be at rest relative to one object and at the same time it may be in motion relative to another object.
Hence, an object can be at rest as well as in motion relatively at the same time.
Is the motion of the earth visible to us?
The motion of the earth is not visible to us because it is a relative motion.
Although the phenomenon like formation of day and night indicates the motion of the earth about its own axis.
Give two examples of scalar quantities.
Two examples of scalar quantities are mass and volume.
Give two examples of vector quantities.
Examples of vector quantities are velocity and acceleration.
Define the term displacement.
Displacement is the shortest distance travelled by a body in the direction from initial to final position.
Is displacement a scalar quantity?
No, displacement is a vector quantity as it has both magnitude and direction.
If the displacement of a body is zero, is the distance covered by it necessarily zero?
No, it is not necessary that the distance covered by a body is zero when its displacement is zero. Displacement can be zero even when distance is zero.
Can the displacement be greater than the distance travelled by an object?
No, the displacement of an object can be either equal to or less than the distance travelled by the object.
Under what condition will the distance and displacement of a moving object have the same magnitude?
When the object moves along the same straight line in the same fixed direction, distance and displacement are equal.
Two cars moving in opposite directions cover same distance d in one hour. If the cars were moving in north-south direction, what will be their displacement in one hour?
Displacement of one car = d, due south.
Displacement of other car = d, due north.
Ravi told his friend that his house is 1 km towards south from the Main Post Office. Express displacement and the distance moved by the friend from the Post Office when he arrives at Ravi’s house. Mention the reference point chosen.
We have considered Post Office as the reference point or origin.
(i) Distance moved by the friend in going from Post Office to Ravi’s house = 1 km.
(ii) Displacement moved by the friend in going from Post Office to Ravi’s house = 1 km, due south.
A body is moving along a circular path of radius r. What will be the distance and displacement of the body when it completes half a revolution?
A body is moving along a circular path of radius 'r'.

Displacement is a __________ quantity and distance is a __________ quantity.
vector, scalar.
Is speed a vector quantity?
No, speed is a scalar quantity as it possesses only magnitude and not direction.
Which of the following is a scalar quantity?
(i) Moment of a force (ii) power (iii) electric field.
Power is a scalar quantity.
Which of the following is a scalar quantity?
(i) Momentum (ii) acceleration (iii) electric energy.
Electric energy.
Which of the following are vector quantities?
(i) Mass (ii) displacement (iii) speed (iv) velocity.
Displacement and velocity.
Is electric potential a scalar or a vector quantity?
Electric potential is a scalar quantity.
A body is moving with a velocity of 10 m/s. If the motion is uniform, what will be the velocity after 10 s?
Given, that the motion is uniform. Therefore, the velocity will remain the same after 10 seconds. That is 10 m/s.
Can the average speed of a moving body ever be zero?
Speed is a scalar quantity and is always positive. So, it's average speed can never be zero.
What is the angle between two vectors when their sum is maximum?
The angle between two vectors when the sum is maximum is 0°.
What is the angle between two vectors when their sum is minimum?
Angle between two vectors is 180° when their sum is minimum.
Give the name of the physical quantity that corresponds to the rate of change of displacement.
Rate of change of displacement is known as velocity.
Define velocity. What is its SI unit?
The distance travelled by a body per unit time in given direction is called its velocity. The SI unit of velocity is m/s.
What does the speedometer of a car measure—average speed or instantaneous speed?
Instantaneous speed.
What does the reading of the odometer of a vehicle indicate?
Odometer measures the distance moved by the vehicle.
Can the speed of a body vary if its velocity is constant?
When the velocity of a body is constant, speed is also constant.
Can a body have constant speed but variable velocity?
Yes, a body can have constant speed but variable velocity.
For example, a body in uniform circular motion has constant speed but its velocity changes at every point during the course of motion.
Whenever, the direction changes, velcoity changes.
Define the term acceleration.
Rate of change of velocity with time is called as acceleration.
What is acceleration of a body moving with uniform velocity?
For a body moving with uniform velocity, acceleration is zero.
When is a body said to have uniform velocity?
When a body covers equal distances in equal intervals of time, in a given direction, the body is said to be moving with a uniform velocity.
A body is moving with a velocity of 10 m/s. If the motion is uniform, what will be the velocity after 10 s?
We have a body moving with velocity 10 m/s and the motion is a uniform motion.
So, after 10 seconds, the body will move with the same velocity, i.e., 10 m/s.
Give one example of uniformly accelerated motion.
A body falling freely to the ground has a uniform acceleration of 9.8 m/s2 is an example of uniformly accelerated motion.
Define uniform circular motion.
When a body moves along a circular path with uniform speed, the motion is called uniform circular motion.
What can you say about the motion of a body if its distance-time graph is a straight line?
If the distance-time graph is a straight line, the body possesses uniform speed.
What does the slope of a distance-time graph indicate?
The slope of the distance-time graph gives us the speed of the body.
If the distance-time graph is parallel to the time-axis, what can you say about the motion of the body?
If the distance-time graph is parallel to the time axis, the body is at rest.
What does the slope of a speed-time graph indicate?
Slope of a speed-time graph gives us acceleration.
Acceleartion = dv/dt
What do we get from the area between the speed-time graph of a body and the time-axis?
The area between the speed-time graph f a body and time axis measures the distance travelled by the body.
If the velocity-time graph of a body is a line parallel to the time-axis, what would be the acceleration of the body?
Zero, because the body possesses uniform velocity.
A body goes round the sun with constant speed in a circular orbit. Is the motion uniform or accelerated?
The motion of body around the sun in a circular orbit is accelerated.
A satellite goes round the earth in a circular orbit with constant speed. Is the motion accelerated?
Yes, the motion of satellite around the earth in a circular orbit is accelerated.
Why is the motion in a circle at a constant speed called accelerated motion?
The velocity of the rotating body changes continuously due to the change in its direction at every point of its motion. Hence, a circular motion is called an accelerated motion.
A graph drawn between speed and time for a moving body is found to be a straight line parallel to the time-axis. What conclusion can you draw from the graph about the speed of the body?
The body is moving with a constant speed if the speed-time graph is a straight line parallel to the time axis.
What is meant by uniform motion ? Can you think of an example of a body in uniform motion?
If a body covers equal distances in equal intervals of time it is said to be in uniform motion.
For example, if a body in uniform motion covers 100 m in 50 s, then it must cover 10 m in every 5 s, 1.0 m in every 0.5 s, 0.1 m in every 0.05 s and so on.
Can a body have:
(i) a uniform speed, but still have acceleration, and
(ii) a zero velocity, but still have acceleration? Give an example of a each kind?
(i) A body can have acceleration even when it has uniform speed. A body in uniform circular motion has uniform speed but at every point its direction of velocity changes, so its motion is accelerated.
(ii) Yes, a body can have acceleration even when its velocity is zero. When a body is thrown up, at highest point its velocity is zero but it has acceleration equal to acceleration due to gravity.
What can you say about the motion of a body, if its velocity-time graph is a straight line?
Here two possibilities exist:
(i) The body has a uniform velocity, if the velocity-time graph is a straight line parallel to the time-axis.
(ii) If the velocity-time graph is inclined to the time-axis at certain angle, the body has uniform acceleration.
What can you conclude from the following graphs about the state of motion of an object?
(i) Displacement-time graph is parallel to the time-axis
(ii) Velocity-time graph is a straight line making an angle with the time-axis.
The conclusions are:
(i) The body is at rest when the displacement-time graph is parallel to the time axis.
(ii) The body has uniform acceleration when the velocity-time gaph is slightly inclined with the time axis.
What can you say about the motion of a body, if its
(i) Displacement-time graph is a straight line passing through the origin
(ii) Velocity-time graph is parallel to the time-axis?In both cases (i) and (ii), the body is moving with uniform velocity.
A boy goes to post office with uniform velocity, there he posts a letter and comes back home with the same velocity. Draw a graph of distance and time for his velocity.
Distance-time graph for the motion of the boy is shown in the fig. below. 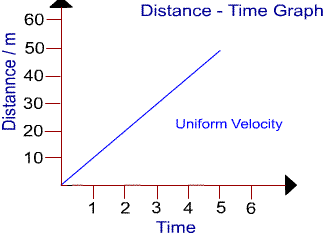
Since, the boy is moving with a uniform velocity, distance-time graph is a straight line.
In this fig. is the distance-time graph of an object. Do you think it represents a real situation? Why?
This distance-time graph does not represent real situation because after 10 hours, the object occupies two different positions simultaneously.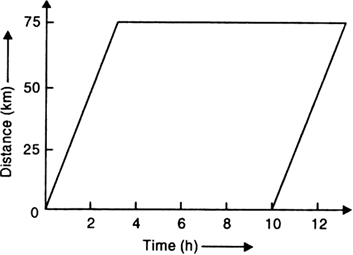
For example, at 10 hours object is at distance 0 km as well as at 75 km which is not physically possible.
A few speed-time graphs for non-uniform motion of objects moving along a straight line are shown in Figs. 8.48(a), (b), (c) and (d).
Tell how the speed is changing with time in each of these graphs? 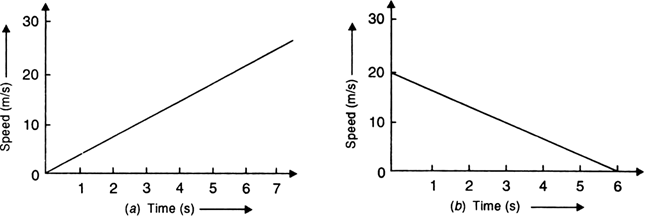
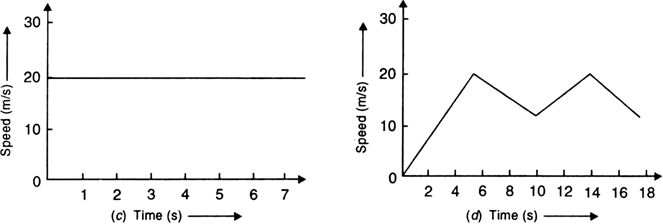
(a) Speed is increasing with time.
(b) Speed is decreasing with time.
(c) Speed is uniform.
(d) Speed is oscillating. That is, it alternately increases and decreases with the passage of time.
The state of motion of an object is represented by the following graphs. What conclusion do you derive about the state of motion of the object in each graph? 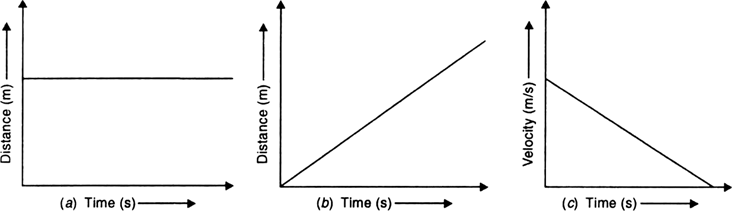
(a) Here, distance-time graph is a straight line. Therefore, the body is at rest.
(b) The body has uniform velocity because distance-time graph is a straight line.
(c) Here, the velocity-time graph has a negative slope. Hence, the body has some initial velocity and is under uniform retardation.
Look at the activities listed below. Reason out whether or not work is done in the light of your understanding of the term ‘work’:
(i) Suma is swimming in a pond.
(ii) A donkey is carrying a load on its back.
(iii) A wind mill is lifting water from a well.
(iv) A green plant is carrying out photosynthesis.
(v) An engine is pulling a train.
(vi) Food grains are getting dried in the sun.
(vii) A sailboat is moving due to wind energy.
(i) Yes, Suma is doing work by pushing water in the backward direction.
(ii) No, because the force exerted by donkey in the upward direction is perpendicular to the horizontal displacement of the load. Hence, no work is done.
(iii) Yes, work is done in lifting water against the force of gravity.
(iv) No, because the leaves of plants remain at rest during photosynthesis.
(v) Yes, engine is doing work in pulling the train. Both the applied force and displacement are in same direction.
(vi) No, because food grains remain at rest.
(vii) Yes, work is done by the wind in moving the sailboat.
An objects thrown at a certain angle to the ground moves in a curved path and falls back to the ground. The initial and the final points of the path of the object lie on the same horizontal line. What is the work done by the force of gravity on the object.
The amount of work done by the force of gravity on the object is zero. This is because the net displacement of the object is in the horizontal direction while the force of gravity acts in the vertical downward direction.
A battery lights a bulb. Describe the energy changes involved in the process.
When a battery lights a bulb, first the battery converts chemical energy into electrical energy. This electrical energy is converted into heat and light.
Certain force acting on a 20 kg mass changes its velocity from 5 ms-1 to 2 ms-1. Calculate the work done by the force.
Given,
Mass, m = 20 kg
Initial velocity, u= 5 ms-1
Final velocity, v= 2 ms-1
Work done = change in K. E.
W = mv2 - mu2
= m ( v2 - u2)
= x 20 x (22 - 52)
= 10 (4-25)
= -10 x 21
= -210 J
Here, the negative sign implies the retarding nature of the applied force.
A mass of 10 kg is at a point A on a table. It is moved to a point B. If the line joining A and B is horizontal, what is the work done on the object by the gravitational force? Explain your answer.
We have,
Mass m kept on table, m = 10 kg
Displacement of mass from A to B is horizontal.
Force of gravitation acts vertically downwards. That is, force acts perpendicular to displacement.
∴ W = Fs cos 90° = 0.
Work done on the object by the gravitaional force is 0.
The potential energy of a freely falling object decreases progressively. Does this violate the law of conservation of energy? Why?
No, the law of conservation of energy is not violated. The loss in potential energy appears as an equal gain in kinetic energy of the object. Hence, the law of conservation of energy remains conserved.
What are the various energy transformations that occur when you are riding a bicycle?
For pulling the bicycle, muscular energy is used. Muscular enrgy is further converted into kinetic energy. A part of the muscular energy is used in doing work against friction on the road. This part of the muscular energy changes into heat.
Does the transfer of energy take place when you push a huge rock with all your might and fail to move it ? Where is the energy you spend going?
While pushing the rock, transfer of muscular energy takes place. This energy is entirely spent in doing work against friction between the rock and the ground.
Since, the rock does not move, no work is done by the body.
A certain household has consumed 250 units of energy during a month. How much energy is this in joules?
Energy consumed by the household = 250 units
1 unit of energy = 1 kWh = 3.6 x 106 J
∴ 250 units of energy = 250 x 3.6 x 106
= 9 x 108 J.
What is the work done by the force of gravity on a satellite moving round the earth? Justify your answer.
When the satellite moves around the earth, the force of gravity acts on it along the radius of its orbit. The direction of motion is along the tangent to the orbit at any point. Thus, force acts perpendicular to displacement. Therefore, the work done on the satellite is zero.
Can there be displacement of an object in the absence of any force acting on it? Think. Discuss this question with your friends and teacher.
Yes, there can be displacement of an object in the absence of any force acting on it.
We know that F = m x a, then m x a = 0 for F = 0
Since mass 'm' cannot be zero, therefore, when force F = 0, then acceleration 'a' = 0. In such a situation, either the object is at rest or it is in uniform motion in straight line. For example, rain drops falling on the earth while the net force on them is zero. There is displacement of the water droplets.A person holds a bundle of hay over his head for 30 minutes and gets tired. Has he done some work or not? Justify your answer.
No work has been done because the bundle of hay remains stationary. That is, the displacement is zero. So, the work done is also zero.
Illustrate the law of conservation of energy by discussing the energy changes, which occur when we draw a pendulum bob to one side and allow it to oscillate. Why does the bob eventually comes to rest? What happens to its energy eventually? Is it a violation of the law of conservation of energy?
Conservation of energy during the oscillations of a simple pendulum. 
Fig. Conservation of energy in a simple pendulum.
i) As shown in the fig. below, a simple pendulum consists of a spherical metal bob suspended by a thread from a fixed support.
ii) As the bob is displaced to end A, it gains potential energy. As it is released from rest, its kinetic energy begins to increase.
iii) At an intermediate position like C, the energy is partly kinetic and partly potential.
iv) At mean position O, the energy is totally kinetic. At the end B, again the energy becomes totally potential. So, total mechanical energy remains constant (= mgh) at all points.
The energy of the body is gradually used in doing work against the force of friction at the point of suspension and also against friction of air. The energy spent is converted into heat. There is no violation of the law of conservation of energy.
Due to decrease in the energy of the bob, its amplitude of oscillation decreases with time and eventually the bob comes to rest.
An object of mass m is moving with a constant velocity v. How much work should be done on the object in order to bring the object to rest?
Work done on the object is equal to the change in kinetic energy of the object.
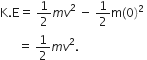
Calculate the work required to be done to stop a car of 1500 kg moving at a velocity of 60 km/h?
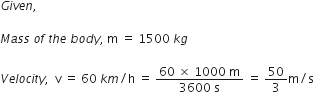
Work required to be done to stop the car,
W = Change in K.E. of the car
In each of the following a force F is acting on an object of mass m. The direction of displacements is from west to east shown by the longer arrow. Observe the diagrams carefully and state whether the work done by the force F is negative, positive or zero.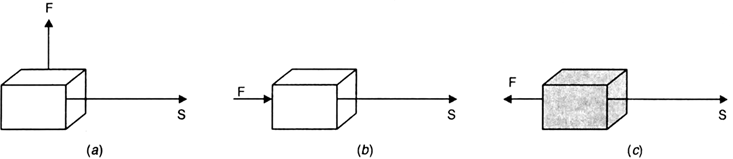
Given,
Force is acting on an object of mass m.
(a) We have,
Force is perpendicular to displacement,
![]()
(b) Here, Force and displacement are in the same direction.
![]()
(c) In this case, Force and s are in opposite direction.
Therefore,

Soni says that the acceleration in an object could be zero even when several forces are acting on it. Do you agree with her? Why?
Yes, the acceleration of the object would be zero when several forces acting on the object add up to give a zero resultant force.
That is,
![]()
A freely falling object eventually stops on reaching the ground. What happens to its kinetic energy on reaching the ground?
When a freely falling object stops on reaching the ground, kinetic energy of the object changes into heat and sound.
Define the term work. State the conditions that need to be satisfied for work to be done. Give some situations in which work is done.
Two conditions need to be satisfied for work to be done are as follows:
(i) Push a pebble lying on a surface. The pebble moves through some distance. Here we apply a force on the pebble and the pebble gets displaced. So, we have done work on the pebble.
(ii) We apply a force to lift a book through a height. The book rises up. We have done work in moving up the book.
(iii) A bullock is pulling a cart. The cart moves. There is a force on the cart and the cart has moved. The bullock has done work on the cart.
How is work done measured when a body moves in the direction of the applied force?
Work done by a constant force when a body moves in the direction of applied force.
As shown in Fig., suppose a force F acts on a body. 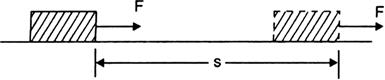
Fig. Work done, when force and displacement are in same direction.
The body moves through a distance s in the direction of the force.
Work done = Force ![]()
i.e., W = F.s
So, work done by a force acting on a body is equal to the magnitude of the force multiplied by the distance moved in the direction of the force.
When is the work done by a force said to be
(i) positive and (ii) negative?
Positive work done is given by,
W = Fs cos 0° = Fs
(i) When a body falls freely under gravity (θ = 0°), the work done by the force of gravity is positive.
Negative work done is given by,
W = Fs cos 180°
= Fs (-1)
= - Fs
Examples:
(i) When a body is lifted up, the work done by the gravitational force is negative. Gravitational force is acting downwards and weight is lifted up.
Name and define the SI unit of work.
The SI unit of work is joule (J).
1 Joule is the amount of work done on an object when a force of 1 N displaces it by 1 m along the line of action of the force.
Thus, 1 joule = 1 newton x 1 metre
1 J = 1 Nm.
Is work done a scalar or vector quantity?
Work done is a scalar quantity because it has only magnitude and no direction.
A force of 7 N acts on an object. The displacement is say 8 m in the direction of the force. Let us take it that the force acts on the object through the displacement. What is the work done in this case?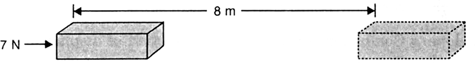
Force acting on the body, F = 7 N
Displacement, s = 8 m
Therefore,
Work done = Force x Displacement
= 7Nx8m
= 56 Nm
= 56 J.
What is the work done when the direction of displacement and the direction of force F acting on a body are perpendicular to each other?
When direction of displacement and direction of force F acting on a body are both perpendicular to each other, work done is zero. The component of the force acting on a body in the direction of its displacement is zero in this case.
Mathematically,
W = Fs cos 90° = 0.
Is it possible that a force is acting on a body but still the work done is zero? Explain giving one example.
OR
What is the work done by a coolie walking on a level road with a load on his head?
Yes, it is possible that a force is acting on a body but the work done is zero.
E.g., Consider a coolie carrying a load on his head across a level road. He exerts an upward force equal to the weight of the load. But the displacement of the load is in the horizontal direction. Thus the angle between force F and displacement s is 0°.
Hence,
W = Fs cos 90° = 0.
Is any work done on a body in uniform circular motion? Justify your answer.
Or
A body is moving along a circular path. How much work is done by the centripetal force?
As shown in the fig. below,
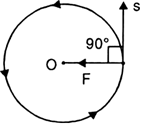
Consider a body being rotated at the end of a string in a circle.
The centripetal force F acts along the radius towards the centre O.
The displacement s acts along the tangent.
Thus, the angle between force F and displacement s is 90°.
Hence,
W = Fs cos 90° = 0.
Thus, no work is done by the centripetal force on a body in uniform circular motion.
When do we say that work is done?
Whenever a force acts on a body and the body is displaced in the direction of the force, work is said to be done.
Write an expression for the work done when a force is acting on an object in the direction of its displacement.
Work done when a force is acting on an object in the direction of its displacement is given by,
Work done = Force x Displacement
Define 1 Joule (J) of work.
One joule of work is done when a force of one newton displaces a body through a distance of 1 metre in its own direction.
A pair of bullocks exerts a force of 140 N on a plough. The field being ploughed is 15 m long. How much work is done in ploughing the length of the field?
We have,
Force exerted, F = 140 N
Displacement, s = 15 m
Therefore,
Work done, W = Fs
= 140 N x 15 m
= 2100 J.
A force of 5 N is acting on an object. The object is displaced through 2 m in the direction of the force, as shown in Fig. 11.5. If the force acts on the object all through the displacement, then what is the work done?
(Textbook Example 11.1)
Consider the object on which the force is acting upon as shown in the fig. below. 
We have,
Force, F = 5 N
Displacement, s = 2 m
Therefore,
Work done, W = Fs = 5N ![]() = 10 Nm = 10 J
= 10 Nm = 10 J
Determine the work done in pushing a cart through a distance of 50 m against the force of friction equal to 150 N.
We have,
Force, F = 150 N
Displacement of the cart, s = 50 m
Work done, W = Fs
= 150 N x 50 m
= 7500 J.
A body of mass 10 kg is displaced through a distance of 2 m under an acceleration of 5 m/s2. Calculate the work done.
Given,
Mass of the body, m - 10 kg
Acceleration, a = 5 m/s2
Displacement, s = 2 m
Therefore,
Work done, W = Fs
Force on the body, F = ma
Therefore,
Work done is given by, W = 50 x 2 J
= 100 J.
A porter lifts a luggage of 15 kg from the ground and puts it on her head 2 m above the ground. Calculate the work done by her on the luggage? Take g - 10 ms-2.
Force applied is equal to the weight of object = mg = 15 x 10 = 150 N
Displacement, s = 1.5 m
Work done, W = Fs = 150 N x 1.5 m
= 225 J.
An object of mass 5 kg is lifted vertically to a height of 2.0 m above the ground. If the acceleration due to gravity at the place is 10 m/s2, what is the amount of work done?
Mass of the object, m = 5 kg
The object is lifted vertically to a height, h = 2 m
Force applied is equal to the weight of object = mg = 5 x 10 = 50 N
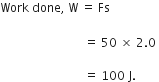
Define the term energy. Give some examples of bodies possessing some energy.
The energy of a body is measured by it's capacity to do certain amount of work. A body does work, implies more energy has been expended.
Some examples of bodies possesing energy are:
(i) When a fast moving cricket ball hits a stationary wicket, it throws away the wicket. The moving ball possesses energy and hence does work on the wicket.
(ii) A hammer raised through a certain height possesses energy. When it falls on a nail placed on a piece of wood, it drives the nail into the wood.
(iii) When a child winds a toy car and place it on the floor, the toy car begins to move. On winding the toy car gains energy and does work in moving against the force of friction.
In the examples given above, different means of doing work is acquired by the object. Hence, these objects are said to posses energy.
How does the energy of an object change when it performs work or work is done on it?
An object loses energy, when work is done by it. When work is done on the object, object gains energy.
How does an object with energy do work?
When an object exerts force on another object, energy is transferred from the former to the latter. The object onto which the enrgy is transferred may start moving as it receives energy and starts moving. Therefore, the first object has the capacity to do some work. This implies, any object that possesses energy can do work.
Is energy a scalar or vector quantity?
Energy is a scalar quantity as it has only magnitude and no direction.
Why are the units of energy the same as those of work ? What is the SI unit of energy?
Energy is measured by the amount of work that a body can do, so units of energy are the same as those of work.
The SI unit of energy is joule (J).
Define 1 J of energy.
One joule of energy is the amount of energy required to do 1 joule of work.
Name a larger unit of energy. How is it related to joule?
A larger unit of energy is kilojoule (kJ).
1 kilojoule = 1000 joule
1 kJ = 1000 J
Name the biggest natural source of energy. Name some other sources of energy also.
The sun is the biggest natural source of energy. We can also get energy from the nuclei of atoms, the interior of the earth and the tides.
Name the different forms of energy.
Different forms of Energy are:
Mechanical energy, sound energy, heat energy, light energy, chemical energy, nuclear energy, electric energy, magnetic energy, solar energy, etc.
What is mechanical energy? What are its two forms?
The energy assosciated with motion and positon of the object is known as mechanical enrgy.
It has two forms :
(i) Kinetic energy and (ii) Potential energy.
What do you understand by kinetic energy of a body? Give some examples.
Kinetic energy:
Kinetic energy is the energy possessed by a body by virtue of its motion. Work is done by a moving object.
The amount of work which a moving object can do before coming to rest is equal to its kinetic energy.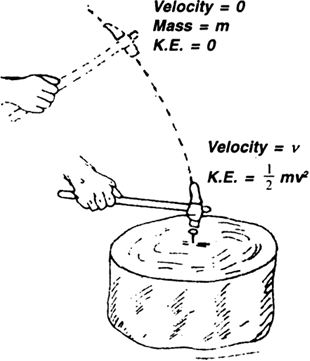
Fig. Conversion of energy into kinetic energy by a hammer.
Examples:
(i) A moving hammer drives a nail into the wood. Being in motion, it has kinetic energy or ability to do work, as shown in Fig. above.
(ii) A fast moving stone can break a window pane. The stone has kinetic energy due to its motion and so it can do work.
(iii) The kinetic energy of air is used to run windmills.
(iv) The kinetic energy of running water is used to run water mills.
(v) A bullet fired from a gun can pierce a target due to its kinetic energy.
Show that the kinetic energy of a body of mass m moving with velocity v is given by![]()
Expression for kinetic energy:
The kinetic energy of a body can be determined by calculating the amount of work required to set the body into motion with the velocity v from its state of rest.
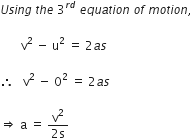
Let m be the mass of the body,
u is the initial velocity of the body,
F = force applied on the body,
a = acceleration produced in the body in the direction of force,
v = final velocity of the body, and
s = distance covered by the body
Now, work done is given by, considering that force and displacement are in the same direction.
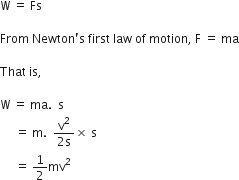
This work done appears as the kinetic energy of the body, given by
![]() , is the kinetic energy of the body.
, is the kinetic energy of the body.
State the factors on which the kinetic energy of a body depends.
Kinetic energy of a body depends upon:
(i) K.E. of a body is directly proportional to its mass.
K.E. ∝ m.
(ii) K.E. of a body is directly proportional to the square of its velocity.
K.E. ∝ v2.
What is the kinetic energy of an object?
Kinetic energy is the energy possessed by an object by virtue of its motion.
Write an expression for the kinetic energy of an object.
The kinetic energy possessed by an object of mass 'm' moving with a uniform velocity 'v' is given by,
Ek = mv2
where,
m is the mass of the object
v is the velocity with which the object is moving.
What happens to the kinetic energy of an object when its velocity is doubled?
The kinetic energy becomes four times its initial value when the velocity of the object is doubled .
Ek ∝ v2
A mass of 10 kg is dropped from a height of 50 cm.
Just as it reaches the ground, does the velocity depend on the mass of the particle? Explain.
The velocity does not depends on the mass of the particle because the acceleration due to gravity under which the particle falls does not depend on mass.
A car is moving with uniform velocities: 18 km/h, 36 km/h, 54 km/h and 72 km/h at some intervals. Calculate the kinetic energy of the boy of 40 kg sitting in the car at these velocities. Plot a graph between the kinetic energy and the velocity. What is the nature of the curve?
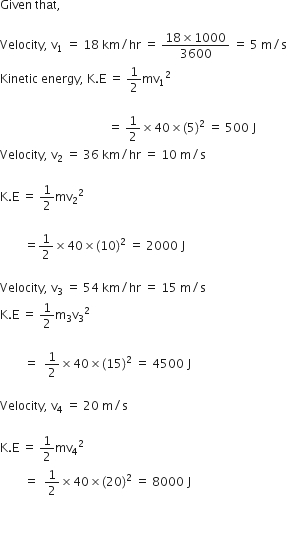
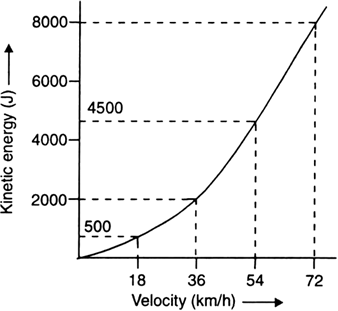
Fig. 11.9. Graph between K.E. and velocity.
The graph between K.E. and velocity is a parabolic curve as shown in the fig. below.
This is because kinetic energy has a direct dependence on square of velocity.
What is meant by potential energy of a body? Give some examples.
Potential energy is the energy possessed by a body by virtue of its position or shape.
Examples of P.E. due to position:
(i) Water stored in dam has potential energy,
(ii) A stone lying on the roof of the building has potential energy.
Examples of P.E. due to shape:
(i) In a toy car, the wound spring possesses potential energy. As the spring is released, its potential energy changes into kinetic energy which moves the toy car.
Fig. 11.10. P.E. stored in a wound spring.
Fig. 11.11. P.E. stored in a stretched bow.
(ii) A stretched bow possesses potential energy. As soon as it is released, it shoots the arrow in the forward direction with a large velocity. The potential energy of the stretched bow gets converted into the kinetic energy of the arrow.
What is gravitational potential energy.
Deduce an expression for the gravitational P.E. of a body of mass m placed at a height h above the ground.
Gravitational potential energy:
The energy of an object increases when it is raised through a certain height above the ground. This is because work is done on it against gravity. The energy present in such an object is called gravitational potential energy.
The amount of work done in raising the object from the ground to that point against gravity gives us the gravitational potential energy.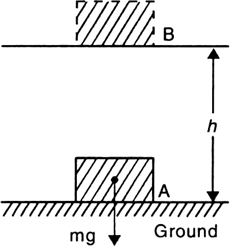
Fig. 11.12. Measurement of P.E.
Expression for potential energy
Consider a body of mass m lying at point A on the earth's surface, where its potential energy is taken as zero.
Weight of object = mg, acting vertically downwards.
In order to lift the body to another position B at a height h, we have to apply a minimum force equal to mg in the upward direction.
So work is done on the body against the force of gravity, is given by
Work done = Force x Displacement
![]() W = Fs
W = Fs
But,
F = mg and s = h,
Therefore,
W = mg x h = mgh
The work done (mgh) on the body is equal to the gain in energy of the body.
This is the potential energy (Ep)) of the body.
Thus,
Ep = mgh
Does the gravitational potential energy of a body depend on the path along which the body is moved ? Illustrate your answer with the help of a suitable example.
Consider a body of mass m being raised to a height h vertically upwards from position A to B, as shown in the fig. below.
In the above fig.
(a) The work done against gravity = mgh.
Suppose the body is taken from position A to B along the path ACDEB, as shown in Fig. (b).
During horizontal motions along paths CD and EB, the force of gravity is perpendicular to displacement, so work done is zero.
Work is done only along vertical paths AC and DE.
Therefore, the net work done = mgh, because AC + DE = h.
Hence, we can see that the work is done against gravity and is independent of the path along which the body is moved.
The work done depends only on the initial and final positions of the body.
That is why, gravitational force is called a conservative force.
Find the energy possessed by an object of mass 10 kg when it is at a height of 6 m above the ground.
(The value of g = 9.8 ms-2).
Given,
Mass of the object, m = 10 kg
Height of the object, h = 6 m
Acceleration due to gravity, g = 9.8 ms-2
Potential energy of the object, Ep = mgh
= 10 x 9.8 x 6 J
= 588 J.
An object of mass 12 kg is at a certain height above the ground. If the gravitational potential energy of the object is 480 J, find the height at which the object is with respect to the ground. Given, g = 10 ms-2.
Therefore, the object is at a height of 4 m from the ground.
A boy weighing 50 kg climbs up a vertical height of 100 m. Calculate the amount of work done by him. How much potential energy does he gain ? Take g = 9.8 m/s2.
Mass of the boy, m = 50 kg
Acceleration due to gravity, g = 9.8 m/s2
Vertical height that the boy climbed up, h = 100 m
Work done by the boy = mgh
= 50 x 9.8 x 100
= 49000 J
= 4.9 x 104 J
Gain in P.E. = Work done = 4.9 x 104 J.
A body of mass 25 kg is raised to the top of a building 10 m high and then dropped freely under gravity (g = 10 m/s2):
(a) Calculate the work done in raising the body to the top of the building.
(b) What is the value of the gravitational potential energy at the top of the building?
(c) By what factor will the gravitational potential energy of the same body increase if it is raised to the top of a multistorey building 30 m high?
(d) When will the kinetic energy of the body be maximum?
Given that,
Mass of the body, m = 25 kg
Height to which the object is rasied up, h = 10 m
Acceleration due to gravity, g = 10 m/s2
(a) Work done = mgh
= 25 x 10 x 10 J
= 2500 J.
(b) Gravitational P.E. = work done = 2500 J
(c) Gravitational P.E. at a height of 30 m is,
P.E= 25 x 30 x 10 J = 7500 J
(d) K.E. of the body will be maximum just before the body strikes the ground.
Two bodies A and B of equal masses are kept at heights of h and 2h, respectively. What will be the ratio of their potential energies?
Let the mass of each body be m.
P.E. of body A = mgh
P.E. of body B = mg. 2h

A man drops a 10 kg rock from the top of a 5 m ladder. What is its kinetic energy when it reaches the ground ? What is its speed just before it hits the ground?
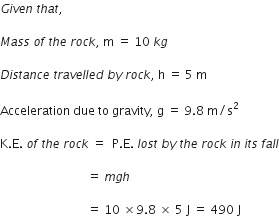
Also,
Kinetic Energy, K.E =
That is,
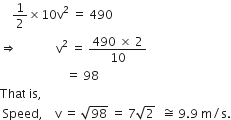
Are various forms of energy inter-convertible?
Yes, energy can be changed from one form to another. The total energy before and after remains the same after conversion of it's forms.
Mention the various energy transformations that take place when we throw a ball.
When we throw a ball, the muscular energy of our body gets converted into the kinetic energy of the ball, thus providing it's motion.
A body is thrown up vertically upwards. Its velocity goes on decreasing. What happens to its kinetic energy as its velocity becomes zero?
When a body is thrown upwards, its kinetic energy gradually changes into potential energy. At the highest point where its velocity becomes zero, whole of the kinetic energy gets converted into potential energy.
What kind of energy transformation takes place when a body is dropped from a certain height. Explain.
When a body is dropped from a certain height, its potential energy gradually changes into kinetic energy. On reaching the ground, the whole of its potential energy gets converted into kinetic energy. But when the ball strikes the ground, the kinetic energy is converted into sound, light and heat.
What kind of energy transformation takes place in the following devices:
(i) Electric heater,
(ii) electric motor,
(iii) dynamo,
(iv) microphone,
(v) headphone,
(vi) hydro-electric power station,
(vii) steam engine,
(viii) solar battery,
(ix) photoelectric cell,
(x) electric cell.
(i) Electric heater: Electrical energy into heat.
(ii) Electric motor: Electrical energy into mechanical energy.
(iii) Dynamo: Mechanical energy into electrical energy.
(iv) Microphone: Sound into electrical energy.
(v) Headphone: Electrical energy into sound.
(vi) Hydroelectric power station: Mechanical energy into electrical energy.
(vii) Steam engine: Heat into mechanical energy.
(viii) Solar battery: Solar energy into electrical energy.
(ix) Photoelectric cell: Light into electrical energy.
(x) Electric cell: Chemical energy into electrical energy.
State the law of conservation of energy. Hence describe the relationship between work and energy.
The law of conservation of energy states that energy can neither be created nor destroyed.
It can only be converted from one form to another.
Work and energy are correlated. Whenever work is done, the object that does work loses energy and the object on which work is done, gains some energy.
For example, when we kick a ball, we lose some energy and the ball gains an equal amount of energy. The energy gained by the ball makes it to move.
Show that when a body is dropped from a certain height, the sum of its kinetic energy and potential energy at any instant during its fall is constant.
Conservation of energy during the free fall of a body.
Let a body of mass m lying at position A be moved to a position B through a height h as shown in the fig. below.
Fig. The free fall of the body is hown below.
The work done on the body is mgh.
The body is at rest at position B.
Therefore,

Explain qualitatively how the total energy of a freely falling body is conserved.
Let us consider an object possesing mass 'm' falling freely from a height 'h'. Initially,
P.E of the body = mgh
K.E of the body = 0 [ body is at rest]
Therefore,
Total energy of the body = mgh+0 = mgh
As the process tails, its potential energy will change into kinetic energy.
At a given instant, v is the velocity of the moving body.
So, K.E of the body =
During the fall, the potential energy would decrease while the kinetic energy would increase. When the object is about to reach the ground, h = 0 and velocity will be maximum. Therefore, the kinetic energy would be maximum and potential energy minimum. However, the total energy of the system, that is, the sum of potential and kinetic energy remains constant.
That is,
Thus, the law of conservation of energy is satisfied.
Explain the term power. Is it a scalar or vector quantity?
The rate of doing work or rate of transfer of enrgy is known as power. If a body does work W in time t, then it's power P is given by,
Power =
Power is a scalar quantity because it is a ratio of two scalarquantities.
At different intervals of time, an agent may perform work. In these cases, average power is the ratio of total energy consumed to the total time taken.
Average power =
Name and define the SI unit of power. Give the bigger power units of power.
The SI unit of power is watt (W).
The power of a body is one watt if it does work at the rate of 1 joule per second.
Also, power is 1 watt when the rate of consumption of energy is 1 Js-1.
1 watt =
Bigger units of power are kilowatt, megawatt and horse power.
1 kilowatt = 1000 watt;
1 kW = 1000 W
1 megawatt = 106 watt;
1 MW = 106 W
1 horse power = 746 watt;
1 H.P. = 746 W.
What is power?
The rate of doing work or the rate of transfer of energy is termed as power.
Define 1 watt of power.
When a body works at the rate of 1 joule per second, the power done is 1 watt.
A lamp consumes 1000 J of electrical energy in 10 seconds. What is its power?
Time taken, t = 10 seconds
Power, P =
Define average power.
Average power of a body is defined as the total energy consumed by it divided by the total time taken.
Average power = Total energy consumed
Total time taken
Name and define the commercial unit of energy. Express it in joules. Where is it used?
Or
Define one kilowatt hour. Express it in joules.
The commercial unit of electric energy is kilowatt-hour (kWh).
One kilowatt hour is defined as the electric energy consumed by an appliance of power 1000 watt in one hour.
1 kWh = 1 kW x 1 h
= 1000 W x 1 h
= 1000 Js-1 x 3600 s
1 kWh = 3600000 J
= 3.6 x 106 J
The electrical energy used in households, industries and commercial establishments is expressed in kilowatt hour.
Electrical energy used is expressed in terms of ‘units’ in our monthly bills.
Here 1 unit means 1 kilowatt hour.
A man does 50 J of work in 5 seconds. What is his power?
Work done, W = 50 J
Time, t = 5 s
Therefore,
Power, P = =
The work done by the heart for each beat is 1 joule. Calculate the power of the heart if it beats 72 times in a minute.
Work done by the heart per beat = 1 J
Work done by the heart in 72 beats, W = 1 x 72
= 72 J
Time Taken, t= 1 min = 60 s
Power, P = =
The heart does 1.5 J of work in each heart beat. How many times per minute does it beat if its power is 2 watt?
Work done during each heartbeat = 1.5 J
Time taken, t = 1 min = 60 s
Power of heartbeat, P = P x t
= 2 Js-1 x 60 s
= 120 J
Number of times heart beats per minute = =
Therefore, the heart beats 80 times per minute.
Calculate the power of a pump which can lift 100 kg of water to store it in a water tank at a height of 19 m in 25 sec. (Take the value of g = 10 m/s2).
Height of the water tank, h = 19 m
Time taken to fill the tank, t = 25 s
Acceleration due to gravity, g = 10 m/s2
Therefore, using the formula,
Power is given by,
P =
Water is falling on the blades of a turbine at the rate of 6 x 103 kg per minute. The height of the fall is 10 m. Calculate the power given to the turbine. Take g = 10 m/s2.
Here,
Mass of water falling on the turbine, m = 6 x 103 kg
Rate at which the water is flowing, t = 1 min = 60 s
Height of the fall, h = 10 m, g = 10 m/s2
So, power given to the turbine, P =
= =10 kW
A woman pulls a bucket of water of total mass 5 kg from a well which is 10 m deep in 10 s. Calculate the power used by her.
Mass of the bucket of water, m = 5 kg
Depth of the well, h = 10 m
Time taken to draw water from the well, t = 10 s
Acceleration due to gravitu, g = 10m/s2
Power is given by, P =
=
Two girls each of weight 400 N climb up a rope through a height of 8 m. We name one of the girls as A and the other as B. Girl A takes 20 seconds while B takes 50 seconds to accomplish this task. What is the power expended by each girl?
Given,
Weight of the girl, mg = 400 N
Height which girl A climbs up, h = 8 m
Time taken, t= 20 s
So, power expended by girl A, P is given by,
(ii) Case 2: Girl B
Given,
Weight of the girl, mg = 400 N
Height which girl B climbs up, h = 8 m
Time taken, t= 50 s
Power expended by girl B is given by,
A boy of mass 50 kg runs up a staircase of 45 steps in 9 seconds. If the height of each step is 15 cm, find his power. Take g = 10 ms-2.
Here we have,
Mass of the body, m = 50 kg
Total number of steps on the staircase = 45
Height of each step = 15 cm
So, height of the staircase, h =
Time taken to climb each step = 9 sec
Now, weight of the boy, mg = 50 x 10 = 500 N
So, power of the boy, P =
What is the power of an engine which supplies 18 kJ of energy per minute?
Energy of the engine, E = 18 kJ
= 18,000 J
Time taken to supply energy, t = 1 min = 60 s
Power, P = , is the required power of the engine.
A tube-well pumps out 2400 kg of water per minute. If water is coming out with a velocity of 3 ms-1, what is power of the pump ? How much work is done, if the pump runs for 10 hours?
Mass of the water being pumped, m = 2400 kg
= 60 s
Velocity with which the water is coming out, v = 3 m/s
Pump runs for 10 hours.
Power of the pump, P =
= = 180 W
A horse exerts a pull on a cart of 300 N so that the horse-cart system moves with a uniform speed 18 km/h on a level road. Calculate the power developed by the horse in watt and also find its equivalent in horsepower.
Speed with which the horse-cart system is moving = 18 km/hr =
Power developed by the horse, P =
Power in terms of horsepower =
An electric bulb of 60 W is used for 6 h per day. Calculate the units of energy consumed in one day by the bulb.
Power of the bulb, P = 60 W = kW = 0.06 kW
Time taken, t = 6 hrs
Therefore,
Energy consumed per day = P
= 0.6 x 6 = 0.36 kWh
= 0.36 units
Calculate the energy consumed by a 100 W refrigerator in 30 days, if it works for 16 hours a day.
The refrigerator works for 16 hours on 30 days.
Power of the refrigerator, P = 100 W = 0.1 kW
Total time, t = 30 x 16 hours
Now, usig the formula for energy, we getEnergy consumed = P x t
= 0.1 kW x 30 x 16 h
= 48 kWh.
A household has a 100 W lamp lighted for 2 hours, two 60 W lamps lighted for 4 hours and an electric fan of 50 W working for 8 hours a day. Calculate the electric units consumed each day.
A 100 W lamp is lighted for two hours.
Two 60 W lamps lighted for 4 hours.
Electric fan of 50 W working for 8 hours a day.
Now, using the formula,
Electric energy consumed by 100 W lamp is,
E= 100 W x 2 h
= 200 Wh
= = 0.20 kWh
Electric energy consumed by two 60 W lamps is,
E= 2 x 60 W x 4 h
= 480 Wh
=
= 0.48 kWh
Electric energy consumed by electric fan is,
E= 50 W x 8 h
= 400 Wh
=
= 0.40 kWh
Thus, total electric energy consumed each day is
T.E = 0.20 + 0.48 + 0.40
= 1.08 kWh
= 1.08 units
A 100 W electric bulb is lighted for 2 hours everyday and five 40 W tubes are lighted for 4 hours everyday. Calculate,
(i) the energy consumed for 60 days and
(ii) the cost of electricity consumed at the rate of Rs. 3 per kWh.
Given,
100 Watt bulb lighted for 2 hours.
Five 40 Watt tubes are lighted for 4 hours everyday.
(i) Energy consumed by a 100 W bulb each day is,
E= 100 W x 2 h
= 200 Wh
= 2001000
= 0.2 kWh
Energy consumed by five 40 W tubes each day,
E = 5 x 40 W x 4 h
= 800 Wh
= 8001000
= 0.8 kWh
Therefore,
Total energy consumed each day = 0.2 + 0.8 = 1.0 kWh
Total energy consumed in 60 days = 1.0 x 60 = 60 kWh
(ii) Cost fo 1 kWh of electricty = Rs. 3
So, cost of 60 kWh = 3 x 60 = Rs. 180.
State the two essential conditions which should be satisfied for work to have been done on an object.
The two conditions to be followed for work done is given below:
(i) a force acts on the body,
(ii) the force has to be applied in the direction of the force.
Define joule.
One joule of work is said to be done when a force of one newton displaces a body through a distance of 1 metre in its own direction.
Moment of force and work done by a force have the same units. Then, what is the difference between them? State at least one point of difference.
Moment of force produces rotatory motion in a body, whereas when a force does work on a body, it produces translatory motion in it.
A coolie is walking on a railway platform with 20 kg load on his head. What is the amount of work done by him? Justify your answer.
Work done is zero because the load does not get displaced from the coolie's head. Hence, the work done is zero.
Therefore, using the formula,
W = Fs cos 90° = 0.
What should be the angle between force and displacement for doing maximum and minimum work?
For maximum work, the angle between force and displacement should be = 0°.
For minimum work, angle between force and displacement = 90°.
A man is holding a suitcase in the state of rest. What is the work done by him?
Work done by the man = 0
Man is in a state of rest and there is no displacement.
Using the formula,
W = Fs cos θ
= F x 0 x cos θ = 0.
What is the amount of work done by a man in pressing a rigid wall with a force of 500 N?
Zero. Because there is no displacement.
What is the work done when a body is moved horizontally along a frictionless surface?
Work done when a body is moved horizontally along a frictionless surface is zero.
In a tug of war, one team is slowly giving way to the other. What work is being done and by whom?
The work is done by the winning team and is equal to the product of resultant force applied by the two teams and the displacement suffered by the losing team.
What is the amount of work done when an artificial satellite revolves around the earth?
An artificial satellite revolves around the earth because of the force of gravity which acts perpendicular to the direction of motion of the satellite.
Therefore, work done is zero when a satellite revolves around the earth.
A boy is running along a circular path with a uniform speed. How much work is done?
Displacement is zero for a circular path because the initial and final point is same. Therefore, the work done is zero.
Does an object in motion have ability to do work?
Yes, an object in motion is capable of doing work because it possesses kinetic energy. Kinetic energy is converted in the form of work done.
Out of energy and acceleration, which one is vector?
Write a formula for the measurement of kinetic energy.1
Kinetic energy of a body, of mass 'm' moving with velocity 'v' is given by,
K.E. = 1/2 mv2.
Write down the expression for gravitational potential energy of a body of mass m placed at a height h above the surface of the earth.
Gravitational P.E. = mgh
where,
m is the mass of the body,
g is the accelaration due to gravity, and
h is the height of the object.
The speed of a car increases four times. What is the increase in its kinetic energy?
Kinetic energy of a moving body is given by,
K.E. ∝ v2.
So, when the speed of car increases 4 times, kinetic energy becomes 16 times of it's initial value.
A body is thrown vertically upward. Its velocity goes on decreasing. What happens to its kinetic energy as its velocity becomes zero?
As the velocity of the body becomes zero when it is thrown vertically upwards, whole kinetic energy gets converted into potential energy. That is, its kinetic energy becomes zero.
Name the form of energy which a wound up watch spring possesses.
Since the body is in a state of rest, it posses potential energy.
Give one example of potential energy due to position.
Water stored in the reservoir of a dam possesses potential energy.
Give an example where a body possesses both kinetic energy and potential energy.
An aeroplane flying at a height has both potential energy and kinetic energy.
Give an example where a body has potential energy due to change of shape.
When a bow is stretched, due to it's change of shape there is a potential energy.
Does a man standing at rest on a moving car possess kinetic energy?
The man sitting inside the car shares the motion of the car. Hence, he posses kinetic energy.
Can a body have momentum without possessing energy?
Any body which has a momentum is in motion. And a moving body has kinetic energy.
Can the kinetic energy of an object be negative?
A kinetic energy of a moving body cannot be negative because both m and v2 are always positive.
Can the potential energy of an object be negative?
When force involved on the bodies are attractive, then potential energy is negative.
Does the potential energy of a spring decrease or increase when it is compressed?
When a spring is compressed, work is done on it and hence the potential energy increases.
An electric cell converts one form of energy into another. Name two forms.
An electric cell converts chemical energy into electrical energy.
So the two forms are:
1. Chemical energy
2. Electrical energy
Name the instrument which transforms electrical energy into mechanical energy.
Electric motor transforms electrical energy into mechanical energy.
What energy transformation takes place when an electric bulb is switched on?
When an electric bulb is switched on, electric energy changes into light and heat.
State the energy transformation in an electric fan.
In an electrical fan, electric energy is converted into mechanical energy.
A bullet strikes a target. The bullet stops but a certain portion of the target is burnt. What is the main energy transformation that has taken place?
When the bullet hits a target, kinetic energy of the bullet gets converted into heat.
What kind of energy transformation takes place at thermal power station?
In a thermal power station, heat energy is converted into electrical energy.
What kind of energy transformation takes place at hydro-electric power plant?
In a hydro-electric power plant, the potential energy of falling water changes into kinetic energy which then changes into electrical energy.
Write relation between Si unit of energy and 1 kWh.
Relation between SI unit of energy and 1 kWh is given by,
1 kWh = 3.6 x 106 J.
Joule is the SI unit of energy.
How much work is done when we push an immovable stone? Justify.
Work done is zero because the distance moved by the immovable stone in the direction of force is zero.
Discuss whether or not work is done in the following cases:
(i) When we twist a wire.
(ii) When we press a football.
(iii) When we push a table.
(iv) When a person carries a hand bag and walks on a level road.
(v) When a person holds a book in his hand and keeps it stationary.
(i) Twisting a wire changes it's shape. So, work is done against internal forces of cohesion between the molecules of the wire.
(ii) The volume of a football changes when we press it. So, work is done against the pressure of the gas inside the bladder of the football.
(iii) Work is done against the force of friction between the legs of the table and the floor, when we push a table between the legs of the table and the floor.
(iv) No work is done in this case. The force the person is applying against the weight of the bag is acting vertically upwards and his motion is in the horizontal direction.Thus, no motion in the direction of the force is applied.
(v) In this case, though the force is constantly being applied, there is no displacement and hence work done is zero.
Explain by an example that a body may possess energy even when it is not in motion.
Consider a stone which is lying on the roof. The stone which is at rest, has a potential energy. The stored potential energy in it is used to lift the stone against the force of gravity.
The stone has a capacity to do an equal amount of work, when it is allowed to fall.
Can you say if the following objects have energy ? If they do, identify whether the energy is kinetic, potential or combination of the two:
(i) A ceiling fan which has been switched off.
(ii) A man climbing a hill.
(iii) A flying bird.
(iv) Water in the reservoir of a dam.
(v) A spring expanded beyond its normal shape.
(vi) A rubber band lying on a table.
(vii) A stretched rubber band lying on the ground.
The enrgy possesed by the object are as given below:
(i) Potential energy
(ii) both kinetic and potential energy
(iii) both kinetic and potential energy
(iv) potential energy
(v) potential energy
(vi) potential energy and
(vii) potential energy
How is energy stored in a watch?
When a watch is winded, work is done in compressing the spring which is stored in it as potential energy. As the spring expands, it does work and moves the hands of the watch.
Why does a driver speed up his vehicle when he moves up a hill?
When a vehicle is moving up the hill, its kinetic energy gradually changes into potential energy. So, to move it up further, it needs more of kinetic energy which is obtained by increasing the speed of the vehicle.
If a body moves along a frictionless path, its energy remains always the same. Why?
A body does not experience any resisting force, while moving ina frictionless surface. Therefore, no work is done by the body. Hence, it's energy remains constant.
Which has greater effect on the kinetic energy of an object : doubling the mass or doubling the velocity?
Kinetic energy is directly proportional to the square of the velocity.
K.E. ∝ v2 and
K.E. ∝ m
Therefore, doubling the velocity has greater effect on the kinetic energy of the object than doubling its mass.
Define kinetic energy and potential energy. Write an expression for the kinetic energy of a body of mass m moving with a velocity v. Find the kinetic energy of a body of mass 40 kg moving with a velocity 15 m/s.
Kinetic energy: Energy possessed by a body by virtue of its motion is called its kinetic energy.
Mathematically, kinetic energy is expressed as,
K.E =
where,
m is the mass of the moving body,
v is the velocity of the body.
Potential energy: Energy possessed by a body by virtue of its position or shape is called its potential energy.
For a body of mass m lying at a height h above the ground level, gravitaional potential energy is given by,
P.E = mgh
Given,
Mass of the body, m = 40 kg
Velocity of the body, v = 15 m/s
So, K. E. = 1 mv2 = 1 x 40 x (15)2 = 4500 J.
2 2
When an arrow is shot, where from the arrow will acquire its kinetic energy?
A stretched bow possesses potential energy due to the change in its shape. The bow is released to shoot an arrow. The potential energy of the bow is converted into the kinetic energy of the arrow.
What change should be affected in the velocity of a body to maintain the same kinetic energy if its mass is increased four times?
Kinetic energy of a body is given by,
K.E. = mv2. ... (1)
From equation (1) we can say that if mass is increased four times, the velocity must be reduced to half to maintain the same kinetic energy.
A boy and girl do the same work in 5 minutes and 10 minutes respectively. Which of these two has more power and why?
Power is given by,
That is, power and time are inversely proportional to each other.
Here, in the given case, as the boy takes less time to do the same work as compared to the girl, so power of the boy is more than that of the girl.
Why do we say that a lift delivers more power in taking a man up than that delivered by the man climbing stairs through the same height?
Power is given by,
As the lift takes less time in taking the man up, so it delivers more power.
Water at the bottom of water-fall is warmer than at the top. Why?
When water is falling from a height, the mechanical energy (K.E. + P.E.) of the falling water is converted into heat energy. Therefore, because of the heat energy the temperature of water at the bottom of water-fall increases.
Our hands become warm when we rub them against each other. Why?
Work is done against the force of friction between the hands, when we rub our hands against each other. The work done, which is the mechanical energy is converted into heat energy. So, our hands get warm.
The head of nail becomes warm when it is hammered into a plank of wood. Explain the series of energy transformations that have taken place.
When the moving hammer strikes the head of the nail, the kinetic energy of the moving hammer is converted into heat energy. As a resukt of the heat energy, the temperature of head of the nail increases.
In a thermal power station, coal is used for the generation of electricity. Mention how energy changes from one form to another before it is transformed into electrical energy?
Energy transformations in a thermal power station is as follows:
The heat energy produced due to combustion of coal converts water into steam. The heat energy of steam is converted into mechanical energy when it turns blades of a turbine. The mechanical energy so obtained is converted into electrical energy by the generators.
A girl sits and stands repeatedly for 5 minutes. Draw a graph to show the variation of potential energy of her body with time.
Consider the sitting position of the girl as the position of zero potential energy.
Let,
h = position of centre of gravity while standing above the sitting position.
m = mass of the girl.
Potential energy while standing = + mgh
P.E while sitting = zero.
There is no acceleration or deceleration while standing and sitting.
Given that, sitting and standing is repeated after every minute.
The graph for the repeated motion is shown below: 
Distinguish between work, energy, and power. State the SI units for each of these quantities.
When a force acts on a body and the body moves in the direction of the force, work is done.
SI unit of work is joule.
The ability of a body to do work is known as energy.
SI unit of energy is Joule.
The rate of doing work is called power.
SI unit of power is watt.
Work done is measured by
mass x velocity
mass x acceleration
force x distance
force x time
C.
force x distance
wound watch spring has
no energy stored in it
mechanical P.E. stored in it
mechanical K.E. stored in it
electrical energy stored in it.
B.
mechanical P.E. stored in it
When the speed of a moving object is doubled, its
acceleration is doubled
weight is doubled
kinetic energy is doubled
kinetic energy increases four times
D.
kinetic energy increases four times
When a body is projected into space, there is an increase in its
kinetic energy
potential energy
momentum
mass
B.
potential energy
When the speed of a moving object is doubled, its
acceleration is doubled
weight is doubled
kinetic energy is doubled
kinetic energy increases four times.
D.
kinetic energy increases four times.
No work is done when
a nail is plugged into a wooden board
a box is pushed along a horizontal floor
there is no component of force parallel to the direction of motion
there is no component of force normal to the direction of force
C.
there is no component of force parallel to the direction of motion
Potential energy of your body is minimum when you
are standing
are sitting on a chair
are sitting on the ground
lie down on the ground
D.
lie down on the ground
Give reason for the following observation:
The smell of hot sizzling food reaches you several meters away, but to get the smell from cold food you can have to go close.
The rate of diffusion is very high in case of gases. The particle of hot sizzling food mixes with the particles of air and reaches us several meters away. In case of cold food the food particles do not mix with the particles of air easily. The temperature increases the rate of diffusion. Hence we have to go close to it get the smell.
A diver is able to cut through water in a swimming pool. Which property of matter does this observation show?
This shows that liquids are compressible. The intermolecular space between the particles of liquid is greater as compared to the solids. Hence when the diver into water the particles of water to get compressed.
What are the characteristics of the particles of matter?
(i) Particles of matter are continuously moving, that is they possess kinetic energy.
(ii) Particles of matter intermix on their own with other. They do so by getting into the spaces between the particles.
The mass per unit volume of a substance is called (density = mass/volume).
Arrange the following in order of increasing density- air, exhaust from chimney, honey, water, chalk, cotton, and iron.
The given substance in the increasing order of their densities can be represented as:
Air< Exhaust form chimney< Cotton< Water< Honey< Chalk<Iron.
Tabulate the differences in the characteristics of states of matter.
|
S.No |
Solid state |
Liquid state |
Gaseous state |
|
1 |
Definite shape and volume |
No definite shape. Liquids attain the shape of the vessel in which they kept. |
Gases have neither a definite shape nor a definite volume. |
|
2. |
There is little space between the particles of solid. |
These particles have a greater space between them. |
The space between gas particles is the greatest. |
|
3. |
Incompressible |
Compressible |
Highly compressible |
|
4. |
These particles attract each other very strongly |
The force of attraction between liquid particles is less than solid particles |
The force of attraction is least between gaseous particles.
|
|
5. |
Rigid |
These particles move freely |
Gaseous particles are in a continuous, random motion. |
|
|
|
|
|
Comment upon the following: rigidity, compressibility, fluidity, filling a gas container, shape, kinetic energy, and density,
Rigidity: Rigidity is property shown by solids. It relates to tendency of solids to resist any change in their shape when an external force is applied. If enough force is applied solids may breaks but do not change their shapes, liquids are not at all rigid as they change their shape.
Compressibility: compressibility means reduction in the volume of a substance on applying pressure. Solids and liquid are incompressible. This is because there is very empty space between the particles of solids and liquids. For example, you cannot fill more petrol in your car petrol tank even if you apply pressure. On the other hand, gases are easily compressible on applying pressure. It is because there are large empty space between the particles of gases.
Fluidity: fluidity is a property shown by liquids and gases. It means tendency to flow. Liquid and gases can change their shapes when a force is applied externally. This is the reverse of rigidity.
Filling a gas container; a gas container can be filled with a large amount of gas when an external pressure is applied on a gas while filling. In the gas container, the gas particles are compressed into a small volume.
Shape: solids have definite shapes and definite boundaries. Liquid and gases do not have fixed shapes. They acquire the shape of the container in which they are kept.
Kinetic energy: kinetic energy is also called energy of motion since particles of matter always remaining motion, they have kinetic energy.
In solids, the particles are bound to each other with strong inter particle forces of attraction, they have least kinetic energy. In liquid, the particles are less tightly bound to each other as the interparticles force of attraction is lesser then in case of solid particle. The K.E of solid particles and hence the particles of liquid of liquid can move more freely. In gases, the particle are bound by very weak forces of attraction. Gas particles can, therefore move almost freely and have a much higher value of kinetic energy. Also temperature increase, kinetic energy of particles of all kinds of matter increases.
Density: density is mass per unit volume. Density means how compact a substance is. Solid, because their particles are tightly packed, occur smaller volume and have greater densities. Gases have particles which can move around freely and therefore they can occupy more volume therefore, gases have least density.
Give reasons:
A gas fills completely the vessel in which it is kept.
This is because the gases have large inter-particle spaces and the inter-particle attraction force is very weak. The gaseous particle can move freely into the empty spaces of another gas as particles of gas have very high kinetic energy. This property of gases is called diffusion. A gas can mix with any other gas easily and move rapidly from one part of vessel to another part of vessel. Therefore, gas particles can spread easily and fill the whole vessel.
Give reasons:
A gas exerts pressure on the walls of the container.
Particles of gas move randomly in all directions at high speed. As a result, the particles hit each other and also hit the walls of the container with a force. Therefore, gas exerts pressure on the walls of the container.
Give reasons:
A wooden table should be called a solid.
A wooden table has a definite shape and volume. It is very rigid and cannot be compressed i.e., it has the characteristics of a solid. Hence, a wooden table should be called a solid.
Give reasons:
We can easily move our hand in air but to do the same through a solid block of wood we need a karate expert.
Particles of air have large spaces between them. On the other hand, wood has little space between its particles. Also, it is rigid. For this reason, we can easily move our hands in air, but to do the same through a solid block of wood, we need a karate expert.
Convert the following temperature to celsius scale:
(a) 300 K. (b) 573 K.
The conversation factor for temperature in celsius scale to kelvin scale is:
Temperature in kelvin = 273 + Temperature in celsius
Temperature of celsius = Temperature in kelvin - 273
(a) 300 K = 300 - 273 = ![]()
(b) 573 K = 573 - 273 = ![]()
What is the physical state of water at:
![]()
(a) The physical state of water above ![]() is gaseous. It exists in the form of steam at
is gaseous. It exists in the form of steam at ![]() .
.
(b) Water at exactly ![]() starts boiling at 1 atmospheric pressure. At this temperature, water exists in two states liquid as gaseous.
starts boiling at 1 atmospheric pressure. At this temperature, water exists in two states liquid as gaseous.
For any substance, why does the temperature remain constant during the change of state?
During change of state, heat energy is absorbed and used for conversion of one physical state to another. Heat absorbed increase the kinetic energy of particles to overcome the interparticle forces of attraction.
Suggest a method to liquefy atmospheric gases.
In liquid, the particles are closer to each other and have lower kinetic energy than gases. When pressure is applied to gas particles they move closer and loose K.E. and thus change to their liquid state. It is possible to liquefy any gas. i.e., convert gas into liquid by increasing the pressure and decreasing the temperature.
Mock Test Series
Sponsor Area
Sponsor Area








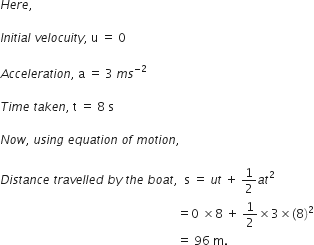
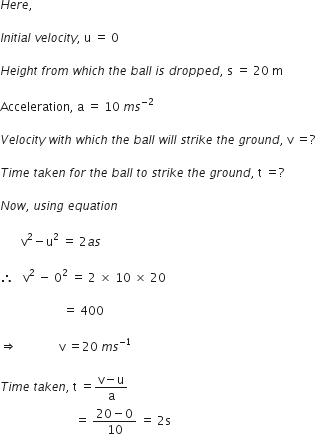


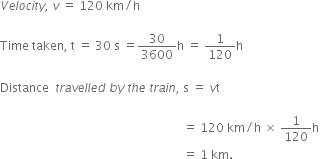
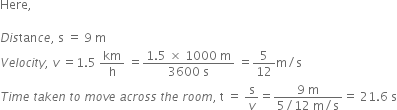


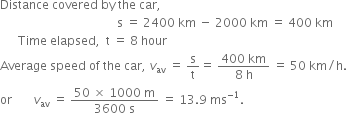

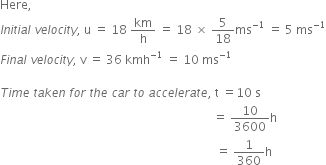
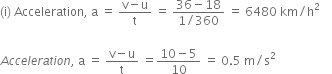
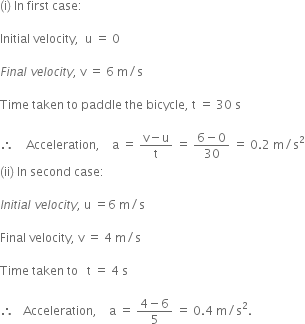
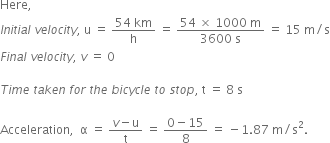
![<pre>uncaught exception: <b>Http Error #404</b><br /><br />in file: /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php line 61<br />#0 [internal function]: com_wiris_plugin_impl_HttpImpl_0(Object(com_wiris_plugin_impl_HttpImpl), NULL, 'http://www.wiri...', 'Http Error #404')
#1 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('com_wiris_plugi...', Array)
#2 [internal function]: _hx_lambda->execute('Http Error #404')
#3 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(532): call_user_func_array(Array, Array)
#4 [internal function]: haxe_Http_5(true, Object(com_wiris_plugin_impl_HttpImpl), Object(com_wiris_plugin_impl_HttpImpl), Array, Object(haxe_io_BytesOutput), true, 'Http Error #404')
#5 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/php/Boot.class.php(769): call_user_func_array('haxe_Http_5', Array)
#6 [internal function]: _hx_lambda->execute('Http Error #404')
#7 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(27): call_user_func_array(Array, Array)
#8 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(444): com_wiris_plugin_impl_HttpImpl->onError('Http Error #404')
#9 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/haxe/Http.class.php(458): haxe_Http->customRequest(true, Object(haxe_io_BytesOutput), NULL, NULL)
#10 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/HttpImpl.class.php(40): haxe_Http->request(true)
#11 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/lib/com/wiris/plugin/impl/TextServiceImpl.class.php(80): com_wiris_plugin_impl_HttpImpl->request(true)
#12 /home/config_admin/public/felixventures.in/public/application/css/plugins/tiny_mce_wiris/integration/service.php(19): com_wiris_plugin_impl_TextServiceImpl->service('mathml2accessib...', Array)
#13 {main}</pre>](/application/zrc/images/qvar/SCEN9014926-2.png)