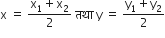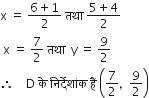गणित Chapter 7 निर्देशांक ज्यामिति
Sponsor Area
NCERT Solution For Class 10 गणित गणित
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए:
(2, 3), (4, 1)
माना बिंदु A(2, 3) और B(4, 1) है।
A और B के बीच की दूरी 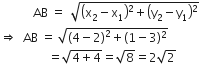
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए:
(– 5, 7), (– 1, 3)
A और B के बीच की दूरी
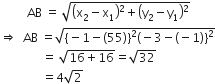
बिंदुओं के निम्नलिखित युग्मों के बीच की दूरियाँ ज्ञात कीजिए:
(a, b), (– a, – b)
माना बिंदु A(a, b) और B(-a, -b) है।
A और B के बीच की दूरी
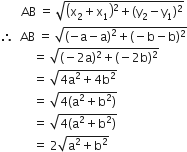
बिंदुओं (0, 0) और (36, 15) के बीच की दूरी ज्ञात कीजिए। क्या अब आप अनुच्छेद 7.2 में दिए दोनों शहरों A और B के बीच की दूरी ज्ञात कर सकते हैं?
A और B के बीच की दूरी
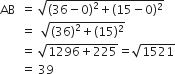
दोनों शहरों के बीच की दूरी 39km होगी।
निर्धारित कीजिए कि क्या बिंदु (1, 5), (2, 3) और (-2, -11) संरेखी हैं।
माना बिंदु A(1, 5), B(2, 3) और C(-2, -11) हैं।
बिंदुओं के बीच की दूरी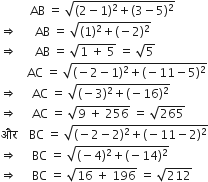
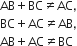
जाँच कीजिए कि क्या बिंदु (5, -2), (6, 4) और (7, -2) एक समद्विबाहु त्रिभुज के शीर्ष हैं।
बिंदुओं के बीच की दूरी
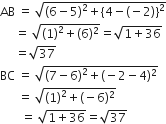
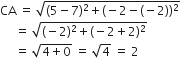
अत: AB = BC
इसलिए यह एक समद्विबाहु त्रिभुज है।
किसी कक्षा में, चार मित्र बिंदुओं A, B, C और D पर बैठे हुए हैं, जैसाकि आकृति में दर्शाया गया है। चंपा और चमेली कक्षा के अंदर आती हैं और कुछ मिनट तक देखने के बाद, चंपा चमेली से पूछती है, 'क्या तुम नहीं सोचती हो कि ABCD एक वर्ग है?' चमेली इससे सहमत नहीं है। दूरी सूत्र का प्रयोग करके, बताइए कि इनमें कौन सही है।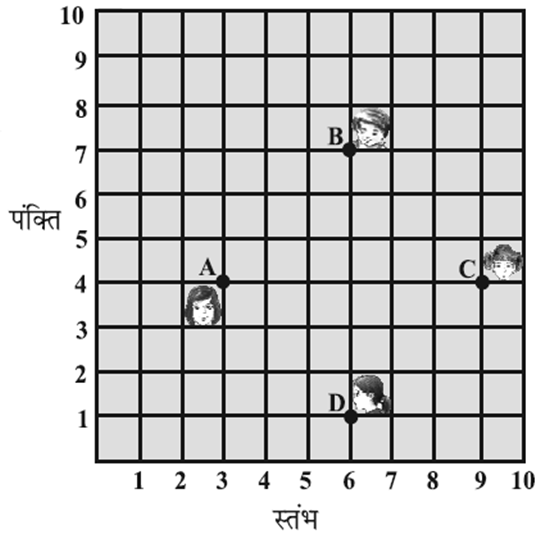
बिंदु A=(3, 4), B=(6, 7), C=(9, 4) तथा D=(6,1)
वर्ग में चारों भुजाएँ बराबर तथा समकोण होती हैं। (या विकर्ण बराबर होते हैं)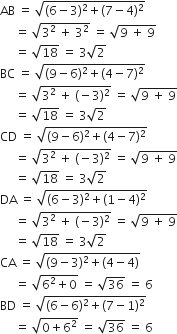
AB = BC = CD = DA तथा AC = BD
अत: ABCD एक वर्ग है अर्थात चम्पा ने ठीक कहा।
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(-1, -2), (1, 0), (-1, 2), (-3, 0)
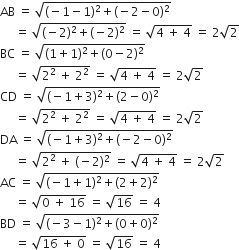
यहाँ AB = BC = CD = DA तथा AC = BD
अत: चतुर्भुज वर्ग होगा।
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(–3, 5), (3, 1), (0, 3), (–1, – 4)
माना A=(–3, 5), B=(3, 1), C=(0, 3), D=(–1, – 4)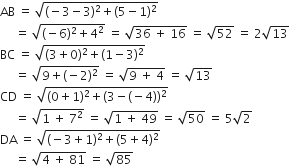
यहाँ 
अत: यह चतुर्भुज है जिसकी भुजाएँ बराबर नहीं हैं।
निम्नलिखित बिंदुओं द्वारा बनने वाले चतुर्भुज का प्रकार (यदि कोई है तो) बताइए तथा अपने उत्तर के लिए कारण भी दीजिए:
(4, 5), (7, 6), (4, 3), (1, 2)
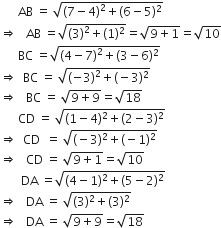

 चतुर्भुज की सामने की भुजाएँ समान है
चतुर्भुज की सामने की भुजाएँ समान है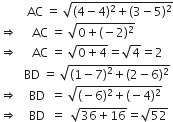
यहाँ AB=CD, BC=DA
चतुर्भुज जिसकी भुजाएँ बराबर हैं। सम्मुख भुजाएँ बराबर हैं। चतुर्भुज एक समांतर चतुर्भुज है।
x-अक्ष पर वह बिंदु ज्ञात कीजिए जो (2, -5) और (-2, 9) से समदूरस्थ हैं।
माना बिंदु P के निर्देशांक (x, 0) हैं।
माना बिंदु हैं A(2, -5) और B(—2, 9)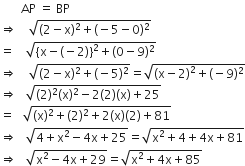
x2 - 4x + 29 = x2 + 4x + 85
⇒ -4x - 4x = 85 - 29
⇒ -8x = 56⇒ x = -7
इसलिए, बिंदु होगा = (-7, 0)
y का वह मान ज्ञात कीजिए, जिसके लिए बिंदु P(2, -3) और Q(10, y) के बीच की दूरी 10 मात्रक है।
दिया है: P(2, -3), Q( 10, y) और PQ = 10 मात्रक
अब, PQ2 = (10)2 = 100
⇒ (10 - 2)2 + {y - (-3)}2 = 100
⇒ (8)2 + (y + 3)2 = 100
⇒ 64 + y2 + 6y + 9 = 100
⇒ y2 + 6y - 27 = 0
⇒ y2 + 9y - 3y - 27 = 0
⇒ y(y + 9) - 3(y + 9) = 0
⇒ (y + 9) (y - 3) = 0
⇒ y + 9 = 0
या y - 3 = 0
⇒ y = - 9
या y = 3
⇒ y = -9, 3
अत: y का मान होगा = -9 या 3
यदि Q(0, 1) बिंदुओं P(5, -3) और R(x, 6) से समदूरस्थ है, तो x का मान ज्ञात कीजिए। दूरियाँ QR और PR भी ज्ञात कीजिए।
P(5, -3), R(x, 6), Q(0, 1)
यह भी दिया है कि,
PQ = RQ
⇒ PQ2 = RQ2
⇒ (0 - 5)2 + {1 - (-3)}2
= (0 - x)2 + (1 - 6)2
⇒ 25 + 16 = x2 + 25
⇒ x2 = 16
⇒ x = ±4
अत: R के निर्देशांक होंगे R(± 4, 6)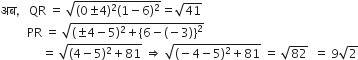
x और y में एक ऐसा संबंध ज्ञात कीजिए कि बिंदु (x, y) बिंदुओं (3, 6) और (-3, 4) से समदूरस्थ हो।
माना P(x, y), Q(3, 6) तथा R(-3, 4)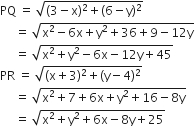
दिया है PQ = PR
⇒ PQ2 = PR2
= x2+y2-6x-12y+45
= x2+y2+6x-8y+25
⇒ 12x+4y-20=0
⇒ 3x+y-5=0
उस बिंदु के निर्देशांक ज्ञात कीजिए, जो बिंदुओं (-1, 7) और (4, 3) को मिलाने वाले रेखाखंड को 2:3 के अनुपात में विभाजित करता है।
x1 = -1, y1 = 7
x2 = 4, y2 = -3
m1 = 2, m2 = 3
माना बिंदु P(x, y)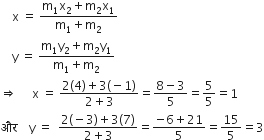
अत: निर्देशांक = (1, 3)
बिंदुओं (4, -1) और (-2, 3) को जोड़ने वाले रेखाखंड को सम-त्रिभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।

माना P और Q रेखाखंड AB को सम-त्रिभाजित करते हैं।
AP = PQ = QB = 1
(i) P, AB को 1:2 में बाँटता है
x1 = 4, y1 = -1
x2 = -2, y2 = -3
m1 = 1, m2 = 2
∴ P के निर्देशांक होंगे (x3, y3)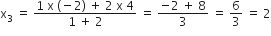
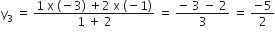
(ii) यहाँ Q, AB को 2:1 में बाँटता है
x1 = 4, y1 = -1
x2 = 2, y2 = -3
m1 = 2, m2 = 1
∴ Q के निर्देशांक होंगे (x4, y4)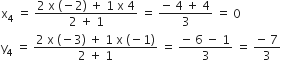
अत: 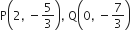
आपके स्कूल में खेल-कूद क्रियाकलाप आयोजित करने के लिए, एक आयताकार मैदान abcd में, चूने से परस्पर 1m की दूरी पर पंक्तियाँ बनाई गई हैं। AD के अनुदिश परस्पर 1m की दूरी पर 100 गमले रखे गए हैं, जैसा कि आकृति में दर्शाया गया है। निहारिका दूसरी पंक्ति में AD के 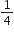 भाग के बराबर की दूरी दौड़ती है और वहाँ एक हरा झंडा गाड़ देती है। प्रीत आठवीं पंक्ति में AD के
भाग के बराबर की दूरी दौड़ती है और वहाँ एक हरा झंडा गाड़ देती है। प्रीत आठवीं पंक्ति में AD के  भाग के बराबर की दूरी दौड़ती है और वहाँ एक लाल झंडा गाड़ देती है। दोनों झंडों के बीच की दूरी क्या है? यदि रश्मि को एक नीला झंडा इन दोनों झंडों को मिलाने वाली रेखाखंड पर ठीक आधी दूरी (बीच में) पर गाड़ना हो तो उसे अपना झंडा कहाँ गाड़ना चाहिए?
भाग के बराबर की दूरी दौड़ती है और वहाँ एक लाल झंडा गाड़ देती है। दोनों झंडों के बीच की दूरी क्या है? यदि रश्मि को एक नीला झंडा इन दोनों झंडों को मिलाने वाली रेखाखंड पर ठीक आधी दूरी (बीच में) पर गाड़ना हो तो उसे अपना झंडा कहाँ गाड़ना चाहिए?
हरे झंडे के निर्देशांक = 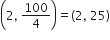
और लाल झंडे के निर्देशांक = 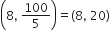
दोनों झंडों के बीच की दूरी
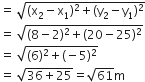
नीले झंडे की स्थिति: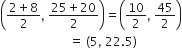
Sponsor Area
बिंदुओं (-3, 10) और (6, -8) को जोड़ने वाले रेखाखंड को बिंदु (-1, 6) किस अनुपात में विभाजित करता है।
माना बिंदु P(-1, 6), Q(-3, 10) और R(6, -8) को मिलाने वाली रेखा को m:1 में विभाजित करता है।
P के निर्देशांक होंगे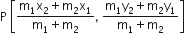
यहाँ,
x1 = -3, y1 = 10
x2 = 6, y2 = -8
m1 = m, m2 = 1
इसलिए, P के निर्देशांक होंगे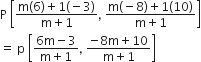
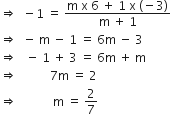
2 : 7
वह अनुपात ज्ञात कीजिए जिसमें बिंदुओं A(1, -5) और B(-4, 5) को मिलाने वाला रेखाखंड x-अक्ष से विभाजित होता है। इस विभाजन बिंदु के निर्देशांक भी ज्ञात कीजिए।
माना x-अक्ष पर स्थिति O बिंदु के निर्देशांक (x, 0) हैं,
माना यह m:1 में विभाजित करता है, y निर्देशांक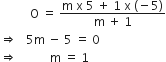
अत: अनुपात = 1:1
x निर्देशांक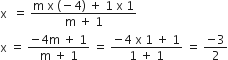
अभीष्ट निर्देशांक (x, 0) = 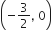
यदि बिंदु (1, 2), (4, y), (x, 6) और (3, 5) इसी क्रम में लेने पर, एक समांतर चतुर्भुज के शीर्ष हो तो x और y ज्ञात कीजिए।
समांतर चतुर्भुज के विकर्णों के मध्य-बिंदु समान होते हैं।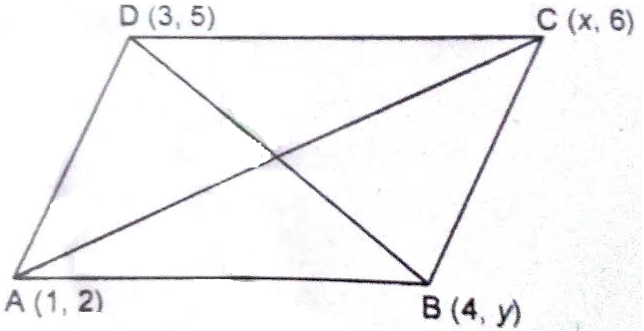
AC का मध्य-बिंदु = 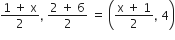
BD का मध्य-बिंदु = 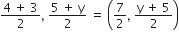
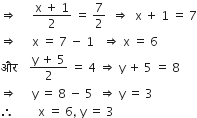
बिंदु A के निर्देशांक ज्ञात कीजिए, जहाँ AB एक वृत्त का व्यास है जिसका केंद्र (2, -3) है तथा B के निर्देशांक (1, 4) हैं।

माना A के निर्देशांक (x, y) हैं। O, AB का मध्य बिंदु है और वृत्त का केंद्र है।
O के निर्देशांक होंगे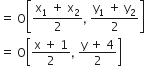
O के निर्देशांक दिए हैं (2, -3)
अत: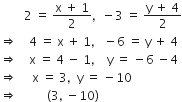
यदि A और B क्रमश: (-2, -2) और (2, -4) हो तो बिंदु P के निर्देशांक ज्ञात कीजिए ताकि 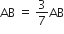 हो और P रेखाखंड AB पर स्थित हो।
हो और P रेखाखंड AB पर स्थित हो।
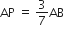
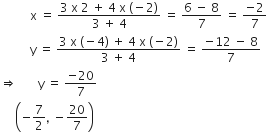
बिंदुओं A(-2, 2) और B(2, 8) को जोड़ने वाले रेखाखंड AB को चार बराबर भागों में विभाजित करने वाले बिंदुओं के निर्देशांक ज्ञात कीजिए।
(i) P बिंदु के लिए:
![]()
यहाँ, m1 = 1, m2 = 3
x1 = -2, y2 = 2
x2 = 2, y2 = 8
P के निर्देशांक:
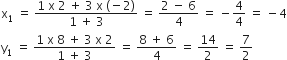
P(x1, y1) = 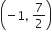
Q बिंदु के लिए:![]()
यहाँ m1 = 2, m2 = 2
x1 = -2, y1 = 2
x2 = 2, y2 = 8
Q के निर्देशांक:
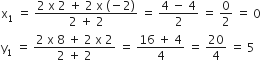
Q(x1, y1) = (0, 5)
R बिंदु के लिए:![]()
यहाँ, m1 = 3, m2 = 1
x1 = -2, y1 = 2
x2 = 2, y2 = 8
R के निर्देशांक:
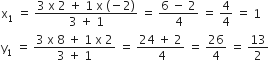
R(x1, y1) = 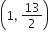
एक समचतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष, इसी क्रम में, (3, 0), (4, 5), (-1, 4) और (-2, -1) हैं। [संकेत: समचतुर्भुज का क्षेत्रफल = 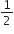 (उसके विकर्णों का गुणनफल)]
(उसके विकर्णों का गुणनफल)]

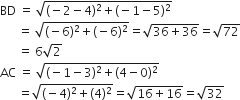
अब, समचतुर्भुज ABCD का क्षेत्रफल
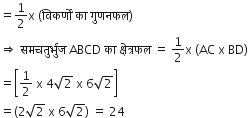
अत: समचतुर्भुज ABCD का क्षेत्रफल = 24 वर्ग इकाई
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं:
(2, 3), (–1, 0), (2, – 4)
बिंदु दिए हैं: A(2, 3), B(-1, 0), C(2, -4)
यहाँ,
x1 = 2, y1 = 3
x2 = -1, y2 = 0
x3 = 2, y3 = -4
∆ABC का क्षेत्रफल
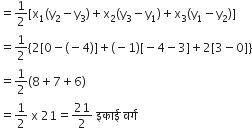
उस त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष हैं:
(–5, –1), (3, –5), (5, 2)
बिंदु दिए हैं: A(-5, -1), B(3, -5) C(5, 2)
यहाँ,
x1 = -5, y1 = -1
x2 = 3, y2 = -5
x3 = 5, y3 = 2
∆ABC का क्षेत्रफल
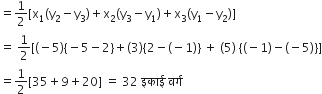
निम्नलिखित में से प्रत्येक में k का मान ज्ञात कीजिए ताकि तीनों बिंदु सरेखी हों:
(7, –2), (5, 1), (3, k)
तीन बिंदु यदि रेखीय हैं, तो
या  का क्षेत्रफल
का क्षेत्रफल

अब,  का क्षेत्रफल
का क्षेत्रफल
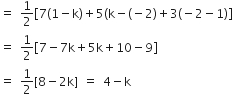

निम्नलिखित में से प्रत्येक में k का मान ज्ञात कीजिए ताकि तीनो बिंदु संरेखी हों:
(8, 1), (k, – 4), (2, –5)
मान लीजिए दिए हुए बिंदु A(8, 1), B(K, -4) और C(2, -5).
यहाँ, हमें प्राप्त हैं:
x1 = 8, y1 = 1
x2 = K, y2 = -4
तथा x3 = 2, y3 = -5
अब, ∆ABC का क्षेत्रफल 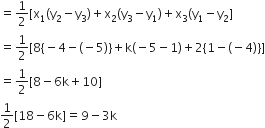
यदि तीन बिंदु संरेखी हैं तो त्रिभुज का क्षेत्रफल = 0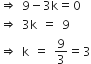
शीर्षों (0, -1), (2, 1) तथा (0, 3) वाले त्रिभुज की भुजाओं के मध्य-बिंदु से बनने वाले त्रिभुज का क्षेत्रफल ज्ञात कीजिए। इस क्षेत्रफल को दिए हुए त्रिभुज के क्षेत्रफल के साथ अनुपात ज्ञात कीजिए।
माना  हैं जिसमें A = (0, -1), B = (2, 1) तथा C = (0, 3)।
हैं जिसमें A = (0, -1), B = (2, 1) तथा C = (0, 3)।
माना AB का मध्य-बिंदु P, BC का मध्य-बिंदु Q तथा CA का मध्य-बिंदु R है।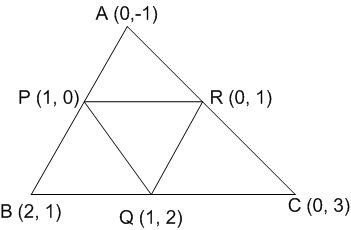
∴ मध्य-बिंदु = 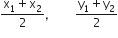
∴ P के निर्देशांक = 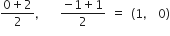
Q के निर्देशांक = 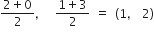
R के निर्देशांक = 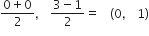
 का क्षेत्रफल =
का क्षेत्रफल = 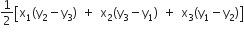
 का क्षेत्रफल =
का क्षेत्रफल = 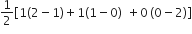
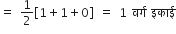 ...(i)
...(i)
 का क्षेत्रफल
का क्षेत्रफल
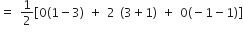
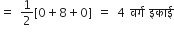 ...(ii)
...(ii) 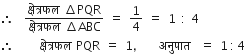
उस चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष इसी कर्म में (– 4, – 2), (– 3, – 5), (3, – 2) और (2, 3).
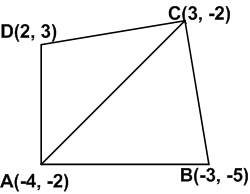
∆ABC का क्षेत्रफल:
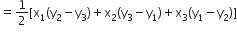
यहाँ हमें प्राप्त हैं,
x1 = -4, y1 = -2
x2 = -3, y2 = -5
x3 = 3, y3 = -2
अब, ∆ABC का क्षेत्रफल:
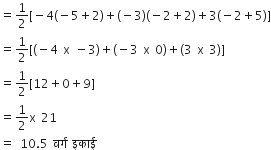
हम जानते हैं, ∆ACD का क्षेत्रफल: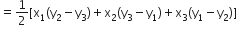
यहाँ हमें प्राप्त हैं,
x1 = -4, y1 = -2
x2 = 3, y2 = -2
x3 = 2, y3 = 3
अब, ∆ACD का क्षेत्रफल: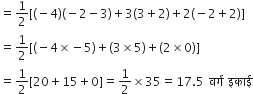
अत: चतुर्भुज ABCD का क्षेत्रफल = ∆ABC का क्षेत्रफल + ∆ACD का क्षेत्रफल
= (10.5 + 17.5) वर्ग इकाई
= 28 वर्ग इकाई
कक्षा IX में आपने पढ़ा है (अध्याय 9, उदाहरण 3) कि किसी त्रिभुज की एक माध्यिका उसे बराबर क्षेत्रफलों वाले दो त्रिभुजों में विभाजित करती है। उस त्रिभुज ABC के लिए इस परिणाम का सत्यापन कीजिए जिसके शीर्ष A(4, – 6), B(3, –2) और C(5, 2) हैं।
यहाँ, हमें प्राप्त हैं:
x1 = 4, y1 = -6
x2 = 3, y2 = -2
और x3 = 5, y3 = 2
∴ ∆ABC का क्षेत्रफल:
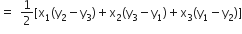
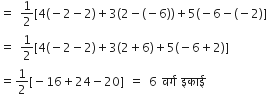
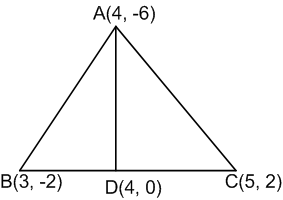
माना D, भुजा AB का मध्य-बिंदु है। अत:AD त्रिभुज, की माध्यिका होगी।
बिंदु D के निर्देशांक होंगे
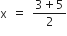 तथा
तथा 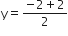
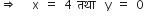
∆ABD में A = (4, -6), B =(3, -2) तथा D = (4, 0)
अत: ∆ABD का क्षेत्रफल: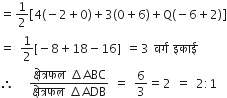
अत:किसी त्रिभुज की माध्यिका, उस त्रिभुज को बराबर क्षेत्रफल के दो भागों में बाँटती है।
बिंदुओं A(2, -2) और B(3, 7) को जोड़ने वाले रेखाखंड को रेखा 2x + y - 4 = 0 जिस अनुपात में विभाजित करती है उसे ज्ञात कीजिए।
मान लीजिए A(2, -2) और B(3, 7) को जोड़ने वाले रेखाखंड को रेखा 2x + y - 4 = 0 को m:1 में विभाजित करती हैं।![]()
विभाजन सूत्र के प्रयोग से:
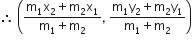
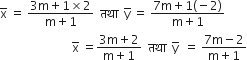
चूँकि 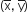 रेखा 2x + y - 4 पर स्थित हैं,
रेखा 2x + y - 4 पर स्थित हैं,
अत: 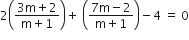
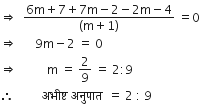
x तथा y में संबंध ज्ञात कीजिए यदि बिंदु (x, y), (1, 2) तथा (7, 0) संरेखी हैं।
 का क्षेत्रफल:
का क्षेत्रफल: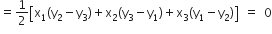
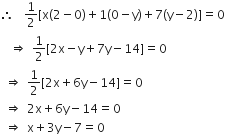
बिंदुओं (6, -6) (3, -7) तथा (3, 3) से गुजरने वाले वृत के केंद्र ज्ञात कीजिए।
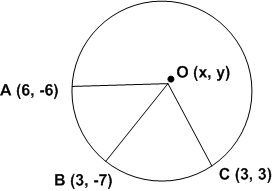
माना वृत्त का केंद्र O(x, y) हैं।
तब, OA = OB = OC
[वृत की त्रिज्या]
⇒ (OA)2 = (OB)2 = (OC)2 ....(i)
समीकरण (i) के प्रयोग से हमे प्राप्त होता हैं,
OA2 = OB2
⇒ (x - 6)2 + (y + 6)2
= (x - 3)2 + (y + 7)2
(x - 6)2 + (y + 6)2 = (x - 3)2 + (y + 7)2
⇒x2 - 12x + 36 + y2 + 12y + 36
= x2 — 6x + 9 + y2 + 14y + 49
⇒ 6x + 2y = 14
⇒ 3x + y = 7 ...(ii)
फिर से, हमे प्राप्त हैं
(OB)2 = (OC)2
⇒ (y + 7)2 = (y - 3)2
⇒ y2 + 49 + 14y = y2 + 9 - 6y
⇒ 20y = 9 - 49
⇒ 20y = 40
⇒ y = -2 ...(iii)
समीकरण (ii) तथा (iii) के प्रयोग से
हमे प्राप्त होता हैं x = 3
अतः वृत्त का केंद्र = (3, -2)
किसी वर्ग के दो सम्मुख शीर्ष (–1, 2) और (3, 2) हैं। वर्ग के अन्य दोनों शीर्ष ज्ञात कीजिए।

तब, AB = BC
⇒ AB2 = BC2
⇒ (x + 1)2 + (y - 2)2 = (x - 3)2 + (y - 2)2
⇒ x2 + 2x + 1 + y2 - 4y + 4 = x2 - 6x + 9 + y2 - 4y + 4
⇒ 8x = 8
⇒ x = 1 में समकोण
में समकोण  है। [∵ ∠B = 90°]
है। [∵ ∠B = 90°]
AB2 + BC2 = AC2 (पाइथागोरस प्रमेय)
⇒ (x + 1)2 + (y - 2)2 + (x - 3)2 + (y - 2)2 = (3 + 1)2 + (2 - 2)2
⇒ x2 + 2x + 1 + y2 - 4y + 4 + x2 - 6x + 9 + y2 - 4y + 4 = 16
⇒ 2x2 + 2y2 - 4x - 8y + 2 = 0
(2 से भाग करने पर)
⇒ x2 + y2 - 2x - 4y + 1 = 0
समीकरण (1) से x का मान समीकरण (2) में प्रतिस्थापित करने पर हमें प्राप्त होता हैं।
⇒ 1 + y2 - 2 - 4y + 1 = 0
⇒ y(y - 4) = 0
⇒ y = 0, 4
अत:वर्ग वांछित शीर्ष (1, 0) और (1, 4) हैं।
कृष्णागर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयातकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1 m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकर घास लगा हुआ लॉन है। इस भूखंड की अंदर एक त्रिभुजाकर घास लगा हुआ लॉन है, जैसाकि आकृति 7.14 में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में फलों के पौधें के बीज बोने हैं।
(i) A को मूलबिंदु मानते हुए, त्रिभुज के शीर्षों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो के शीर्षों के निर्देशांक क्या होंगे?
साथ ही उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
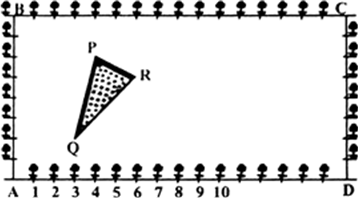
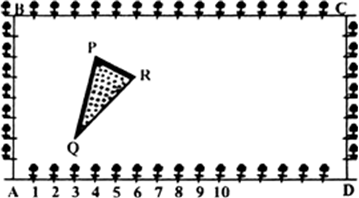
(i) यदि आकृति में A मूल बिंदु हैं, तो
P के निर्देशांक (4, 6) हैं।
Q के निर्देशांक (3, 2) हैं।
R के निर्देशांक (6, 5) हैं।
∆PQR का क्षेत्रफल
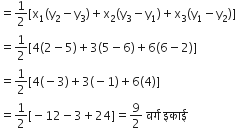
(ii) यदि आकृति में C मूल बिंदु हैं, तो
P के निर्देशांक (12, 2) हैं।
Q के निर्देशांक (13, 6) हैं।
R के निर्देशांक (10, 3) हैं।
∆PQR का क्षेत्रफल 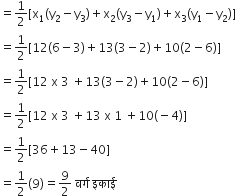
अत: दोनों स्थिति में क्षेत्रफल बराबर हैं।
एक त्रिभुज ABC के शीर्ष A(4, 6) B(1, 5) और C(7, 2) हैं। भुजाओं AB और AC को क्रमश: D और E पर प्रतिच्छेद करते हुए एक रेखा इस प्रकार खींची गई हैं कि 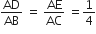 है। Δ ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना Δ ABC के क्षेत्रफल से कीजिए।
है। Δ ADE का क्षेत्रफल परिकलित कीजिए और इसकी तुलना Δ ABC के क्षेत्रफल से कीजिए।
चूँकि 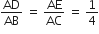 , अत: बिंदु D तथा E, AB तथा AC को 1:3 में विभाजित करता है।
, अत: बिंदु D तथा E, AB तथा AC को 1:3 में विभाजित करता है।
बिंदु के निर्देशांक
सूत्र: 

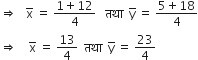
 D के निर्देशांक हैं
D के निर्देशांक हैं 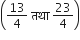
बिंदु E के निर्देशांक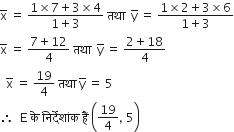
अब त्रिभुज का क्षेत्रफल
सूत्र:
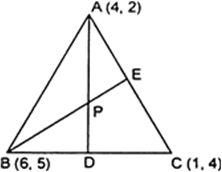
मान लीजिए A(4, 2), B(6, 5) और C(1, 4) एक त्रिभुज ABC के शीर्ष हैं।
AD पर स्थित ऐसे बिंदु P के निर्देशांक ज्ञात कीजिए, कि AP : PD = 2 : 1 हों।
बिंदु P, AD को 2 : 1 में विभक्त करता है।
अत : P के निर्देशांक 
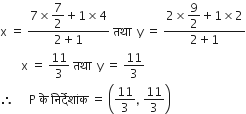
Sponsor Area
मान लीजिए A(4, 2), B(6, 5) और C(1, 4) एक त्रिभुज ABC के शीर्ष हैं।
माध्यिकाओं BE तथा CF ऐसे बिंदु Q तथा R के निर्देशांक ज्ञात कीजिए कि AP:PB = 2 : 1 हों।
E, AC का मध्य-बिंदु है।
अत: के निर्देशांक 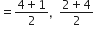
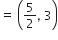
Q, BE को 2 : 1 में बाँटता है। अत: Q के निर्देशांक
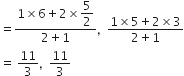
बिंदु F, AE का मध्य-बिंदु है।
अत: F के निर्देशांक 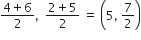
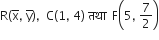 को मिलाने वाली रेखा को 2:1 में बाँटता है।
को मिलाने वाली रेखा को 2:1 में बाँटता है।
अत: R के निर्देशांक = 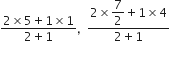
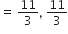
अत: Q तथा R के निर्देशांक 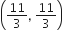 तथा
तथा 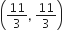 हैं।
हैं।
आप क्या देखते हैं? वह बिंदु जो तीनों माध्यिकाओं का सार्वनिष्ठ है उस त्रिभुज का केन्द्रक कहलाता है और वह प्रत्येक माध्यिका को 2 :1 के अनुपात में विभाजित करता है।
हम देखते हैं कि P, Q तथा R के निर्देशांक समान हैं। अत:P, Q, R से समान बिंदु हैं जिसे केन्द्रक कहते हैं।
मान लीजिए A(4, 2), B(6, 5) और C(1, 4) एक त्रिभुज ABC के शीर्ष हैं।
यदि A(x1, y1), B(x2, y2) और C(x3, y3)  के शीर्ष हैं तो इस त्रिभुज के केन्द्रक के निर्देशांक ज्ञात कीजिए।
के शीर्ष हैं तो इस त्रिभुज के केन्द्रक के निर्देशांक ज्ञात कीजिए।
यदि A(x1, y1), B(x2, y2) तथा (x3, y3) शीर्ष बिंदु हैं तो केन्द्रक के निर्देशांक होंगे:
बिंदुओं A(-1, -1), B(-1, 4) C(5, 4) और D (5, -1) से एक आयत ABCD बनता है। P,Q,R तथा S क्रमश:AB, BC, CD तथा DA के मध्य बिंदु हैं। क्या यह एक आयत है? क्या यह एक समचतुर्भुज है? सकारण उतर दीजिए।
चूँकि P, A(-1, -1) तथा B(-1, 4) का मध्य बिंदु है।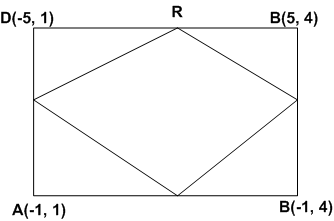
Q, B(-1, 4) तथा C(5, 4) का मध्य बिंदु है।
R, C (5, 4), D(5, -1) का मध्य बिंदु है।
तथा S, D(5, -1) तथा A(-1, -1) का मध्य बिंदु है।
अत: 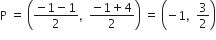
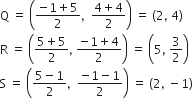
अत: लम्बाई 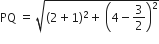
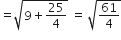
लम्बाई 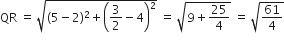
लम्बाई RS = 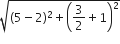
= 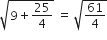
लम्बाई PS = 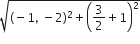
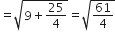
यहाँ PQ = QR = RS = SP
अत: PQRS एक समचतुर्भुज (रोम्बस) है।
बिंदु P का x-निर्देशांक उसके y-निर्देशांक का दुगुना है। यदि बिंदु Q(2, -5) तथा R(-3, 6) से समदूरस्थ है, तो P के निर्देशांक ज्ञात कीजिए।
माना कि बिंदु P (2K, K), Q(2, -5), R(-3, 6)
![]()
PQ = PR ........ [दिया है
PQ2 = PR2 ... दोनों तरफ वर्ग करने पर
(2K - 2)2 + (K + 5)2 = (2K + 3)2 + (K-6)2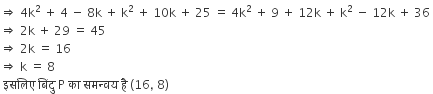
Tips: -
एक बिंदु P(x, y) की भूल बिंदु से दूरी ज्ञात कीजिए।
दिया हुआ बिंदु P (x,y) है
मूल बिंदु) O (0,0) है
दूरी सूत्र का उपयोग करके
वह अनुपात ज्ञात कीजिए जिसमें बिंदु P (4, m), बिंदुओं A (2, 3) तथा B(6, -3) को मिलाने वाले रेखाखण्ड को विभाजित करता है। अतः m का मान ज्ञात कीजिए।
मान लीजिए बिंदु P (4, m) रेखा खंड विभाजित करता है
अनुपात A (2, 3) और B (6, -3) अनुपात K: 1 में शामिल हों
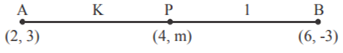
बिंदु के समन्वय,
लेकिन बिंदु P के समन्वय को (4, m) के रूप में दिया जाता है
Mock Test Series
Sponsor Area
Sponsor Area