गणित Chapter 14 सांख्यिकी
Sponsor Area
NCERT Solution For Class 10 गणित गणित
विद्यार्थियों के एक समूह द्वारा अपने पर्यावरण संचेतना अभियान के अंतर्गत एक सर्वेक्षण किया गया, जिसमें उन्होंने एक मोहल्ले के 20 घरों में लगे हुए पौधों से संबंधित निम्नलिखित आँकड़े एकत्रित किए। प्रति घर माध्य पौधों की संख्या ज्ञात कीजिए।
| पौधों की संख्या | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12 | 12-14 |
| घरों की संख्या | 1 | 2 | 1 | 5 | 6 | 2 | 3 |
माध्य ज्ञात करने के लिए अपने किस विधि का प्रयोग किया और क्यों?
|
पौधों की संख्या |
घरों की संख्या (fi) |
वर्ग चिह्न (xi) |
fixi |
|
0-2 |
1 |
1 |
1 |
|
2-4 |
2 |
3 |
6 |
|
4-6 |
1 |
5 |
5 |
|
6-8 |
5 |
7 |
35 |
|
8-10 |
6 |
9 |
54 |
|
10-12 |
2 |
11 |
22 |
|
12-14 |
3 |
13 |
39 |
|
योग |
Σfi = 20 |
|
यहाँ पर, दिया गया हैं,
 = 162
= 162अत:
माध्य
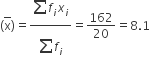
यहाँ पर माध्य ज्ञात करने के लिए हमने प्रत्यक्ष विधि का प्रयोग किया है क्योंकि xi व fi के संख्यात्मक मान छोटे हैं।
किस फैक्ट्री के श्रमिकों की दैनिक मज़दूरी के निम्नलिखित बंटन पर विचार कीजिए:
| दैनिक मज़दूरी (रुपयों में) | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| श्रमिकों की संख्या | 12 | 14 | 8 | 6 | 10 |
यहाँ पर माना कल्पित माध्य (a) = 150
तथा वर्ग-माप (h) = 20 तब 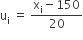
| वर्ग अंतराल | बारंबारता (fi) | वर्ग चिह्न (xi) | ui = 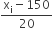 |
fiui |
| 100 - 120 | 12 | 110 | -2 | -24 |
| 120 - 140 | 14 | 130 | -1 | -14 |
| 140 - 160 | 8 | 150 | 0 | 0 |
| 160 - 180 | 6 | 170 | 1 | 6 |
| 180 - 200 | 10 | 190 | 2 | 20 |
| योग |  |
 |
माध्य
 =
= 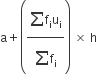
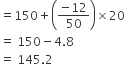
अत: माध्य दैनिक मज़दूरी = ₹ 145.20
निम्नलिखित बंटन एक मोहल्ले के बच्चों के दैनिक जेबखर्च दर्शाता है। माध्य जेबखर्च 18 रु है। लुप्त बारंबारता f ज्ञात कीजिए:
|
दैनिक जेब भत्ता |
11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| बच्चों की संख्या | 7 | 6 | 9 | 13 | f | 5 | 4 |
यहाँ पर माना कलिप्त माध्य (a) = 18
तथा वर्ग-माप (h) = 2 तो 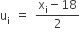
| वर्ग-अंतराल | बारंबारता (fi) | वर्ग चिह्न (xi) | 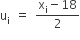 |
 |
| 11-13 | 7 | 12 | -3 | -21 |
| 13-15 | 6 | 14 | -2 | -12 |
| 15-17 | 9 | 16 | -1 | -9 |
| 17-19 | 13 | 18 | 0 | 0 |
| 19-21 | f | 20 | 1 | f |
| 21-23 | 5 | 22 | 2 | 10 |
| 23-25 | 4 | 24 | 3 | 12 |
| योग | 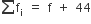 |
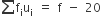 |
अब, माध्य
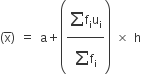
 18 = 18 +
18 = 18 + 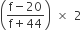

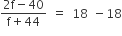
 2f - 40 = 0 x (f + 44)
2f - 40 = 0 x (f + 44)


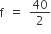
= 20
अत: लुप्त बारंबारता (f) = 20
किसी अस्पताल में, एक डॉक्टर द्वारा 30 महिलाओं की जाँच की गई और उनके ह्रदय स्पंदन (beat) की प्रति मिनट संख्या नोट करके नीचे दर्शाए अनुसार संक्षिप्त रूप में लिखी गई। एक उपयुक्त विधि चुनते हुए, इन महिलाओं के ह्रदय स्पंदन की प्रति मिनट माध्य संख्या ज्ञात कीजिए:
| ह्रदय स्पंदन की प्रति मिनट संख्या | 65-68 | 68-71 | 71-74 | 74-77 | 77-80 | 80-83 | 83-86 |
| महिलाओं की संख्या | 2 | 4 | 3 | 8 | 7 | 4 | 2 |
यहाँ पर माना कल्पित माध्य (a) = 75.5
तथा वर्ग-माप (h) = 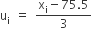
| वर्ग अंतराल | बारंबारता | वर्ग चिह्न | 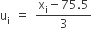 |
 |
| 65-68 | 2 | 66.5 | -3 | -6 |
| 68-71 | 4 | 69.5 | -2 | -8 |
| 71-74 | 3 | 72.5 | -1 | -3 |
| 74-77 | 8 | 75.5 | 0 | 0 |
| 77-80 | 7 | 78.5 | 1 | 7 |
| 80-83 | 4 | 81.5 | 2 | 8 |
| 83-86 | 2 | 84.5 | 3 | 6 |
| योग |  |
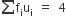 |
अब, माध्य
 =
= 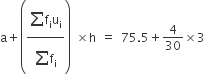
= 75.5 + 0.4 = 75.9
अत: महिलाओं की माध्य ह्रदय स्पंदन गति 75.9 प्रति मिनट है।
किसी फुटकर बाज़ार में, फल विक्रेता पेटियों में रखे आम बेच रहे थे। इन पेटियों में आमों की संख्याएँ भिन्न-भिन्न थीं। पेटियों की संख्या के अनुसार, आमों का बंटन निम्नलिखित था-
| आमों की संख्या | 50-52 | 53-55 | 56-58 | 59-61 | 62-64 |
| पेटियों की संख्या | 15 | 110 | 135 | 115 | 25 |
यहाँ पर,
माना कल्पित माध्य (a) = 57
तथा वर्ग-माप (h) = 3
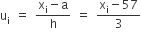
| वर्ग-अंतराल | बारंबारता (fi) | वर्ग चिह्न (xi) | 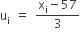 |
fiui |
| 50-52 | 15 | 51 | -2 | -30 |
| 53-55 | 110 | 54 | -1 | -110 |
| 56-58 | 135 | 57 | 0 | 0 |
| 59-61 | 115 | 60 | 1 | 115 |
| 62-64 | 25 | 63 | 2 | 50 |
| योग |  |
 |
अब माध्य
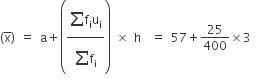
= 57 + 0.1875 = 57.1875
अत: एक पेटी में रखे आमों की माध्य संख्या = 57.19
हमने माध्य ज्ञात करने के लिए पग-विचलन विधि का उपयोग किया है।
निम्नलिखित सारणी किसी मोहल्ले के परिवारों में भोजन पर हुए दैनिक व्यय को दर्शाती है:
| दैनिक व्यय (रुपयों में) | 100-150 | 150-200 | 200-250 | 250-300 | 300-350 |
| परिवारों की संख्या | 4 | 5 | 12 | 2 | 2 |
यहाँ पर माना कलिप्त माध्य (a) = 225
तथा वर्ग-माप (h) = 50
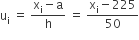
| वर्ग-अंतराल | बारंबारता (f1) | वर्ग- चिह्न (xi) | 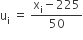 |
 |
| 100-150 | 4 | 125 | -2 | -8 |
| 150-200 | 5 | 175 | -1 | -5 |
| 200-250 | 12 | 225 | 0 | 0 |
| 250-300 | 2 | 275 | 1 | 2 |
| 300-350 | 2 | 325 | 2 | 4 |
| योग |  |
 |
अब, माध्य

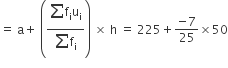

अत: भोजन पर हुआ माध्य दैनिक व्यय = 211 रु
वायु में सल्फर डाइ-ऑक्साइड (SO2) की सांद्रता (भाग प्रति मिलियन में) को ज्ञात करने के लिए, एक नगर के 30 मोहल्ले से आँकड़े एकत्रित किए गए, जिन्हें नीचे प्रस्तुत किया गया है:
| SO2 की सांद्रता | बारंबारता |
| 0.00 - 0.04 | 4 |
| 0.04 - 0.08 | 9 |
| 0.08 - 0.12 | 9 |
| 0.12 - 0.16 | 2 |
| 0.16 - 0.20 | 4 |
| 0.20 - 0.24 | 2 |
यहाँ पर प्रत्यक्ष विधि द्वारा माध्य ज्ञात करेंगे:
| SO2 की सांद्रता | बारंबारता  |
वर्ग चिह्न  |
 |
| 0.00 − 0.04 | 4 | 0.02 | 0.08 |
| 0.04 − 0.08 | 9 | 0.06 | 0.54 |
| 0.08 − 0.12 | 9 | 0.10 | 0.90 |
| 0.12 − 0.16 | 2 | 0.14 | 0.28 |
| 0.16 − 0.20 | 4 | 0.18 | 0.72 |
| 0.20 − 0.24 | 2 | 0.22 | 0.44 |
| योग |  |
 = 2.96 = 2.96 |
अब, माध्य
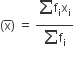
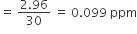
अत: वायु में SO2 की सांद्रता का माध्य = 0.099 ppm
किसी कक्षा अध्यापिका ने पूरे सत्र के लिए अपनी कक्षा के 40 विद्यार्थियों की अनुपस्थिति निम्नलिखित रूप में रिकॉर्ड (record) की। एक विद्यार्थी जितने दिन अनुपस्थित रहा उनका माध्य ज्ञात कीजिए:
| दिनों की संख्या | 0−6 | 6−10 | 10−14 | 14−20 | 20−28 | 28−38 | 38−40 |
| विद्यार्थियों की संख्या | 11 | 10 | 7 | 4 | 4 | 3 | 1 |
यहाँ पर प्रत्यक्ष विधि द्वारा माध्य ज्ञात करेंगे:
| दिनों की संख्या | विद्यार्थियों की संख्या  |
वर्ग- चिह्न  |
 |
| 0−6 | 11 | 3 | 33 |
| 6−10 | 10 | 8 | 80 |
| 10−14 | 7 | 12 | 84 |
| 14−20 | 4 | 17 | 68 |
| 20−28 | 4 | 24 | 96 |
| 28−38 | 3 | 33 | 99 |
| 38−40 | 1 | 39 | 39 |
| योग |  |
 |
अब, माध्य
 =
= 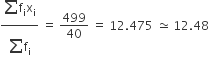
अत: माध्य अनुपस्थिति = 12.48 दिन
निम्नलिखित सारणी नगरों की साक्षरता दर (प्रतिशत में) दर्शाती है। माध्य साक्षरता दर ज्ञात कीजिए:
| साक्षरता दर (% में) | 45−55 | 55−65 | 65−75 | 75−85 | 85−95 |
| नगरों की संख्या | 3 | 10 | 11 | 8 | 3 |
यहाँ पर, माना कलिप्त माध्य (a) = 70
तथा वर्ग-माप (h) = 10
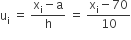
| साक्षरता दर (% में) | बारंबारता  |
वर्ग-चिह्न (xi) | 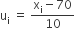 |
 |
| 45−55 | 3 | 50 | −2 | −6 |
| 55−65 | 10 | 60 | −1 | −10 |
| 65−75 | 11 | 70 | 0 | 0 |
| 75−85 | 8 | 80 | 1 | 8 |
| 85−95 | 3 | 90 | 2 | 6 |
| योग |  |
 |
माध्य
 =
= 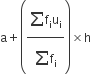
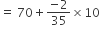
= 70 − 0.57 = 69.43
अत: माध्य साक्षरता दर = 69.43%
निम्नलिखित सारणी किस अस्पताल में एक विशेष वर्ष में भर्ती हुए रोगियों की आयु को दर्शाती है:
| आयु (वर्षों में) | 5−15 | 15−25 | 25−35 | 35−45 | 45−55 | 55−65 |
| रोगियों की संख्या | 6 | 11 | 21 | 23 | 14 | 5 |
यहाँ पर, अधिकतम वर्ग बारंबारता 23 है तथा इसका बारंबारता संगत वर्ग 35 - 45 है। बहुलक वर्ग = 35 - 45
बहुलक वर्ग = 35 - 45
बहुलक वर्ग की निम्न सीमा (l) = 35
वर्ग-माप (h) = 10
बहुलक वर्ग की बारंबारता (f1) = 23
बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता (f0) = 21
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 14
अत: बहुलक = 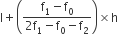
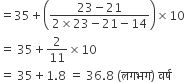
माध्य ज्ञात करने के लिए - माना कलिप्त माध्य (a) = 30
वर्ग-माप (h) = 10
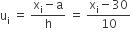
| वर्ग-अंतराल | बारंबारता(fi) | वर्ग चिह्न (xi) | 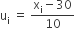 |
 |
| 5−15 | 6 | 10 | −2 | −12 |
| 15−25 | 11 | 20 | −1 | −11 |
| 25−35 | 21 | 30 | 0 | 0 |
| 35−45 | 23 | 40 | 1 | 23 |
| 45−55 | 14 | 50 | 2 | 28 |
| 55−65 | 5 | 60 | 3 | 15 |
| योग |  |
 |
अब, माध्य
 =
= 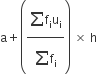
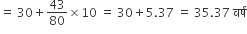
अत: अस्पताल में भर्ती अधिकतम रोगी 36.8 वर्ष आयु (लगभग) के हैं जबकि औसतन अस्पताल में भर्ती किए गए रोगियों की आयु 35.37 वर्ष है।
निम्नलिखित आँकड़े बिजली उपकरणों के प्रेशित जीवनकाल (घंटों में) की सूचना देते हैं:
| जीवनकाल (घंटों में) | 0−20 | 20−40 | 40−60 | 60−80 | 80−100 | 100-120 |
| बारंबारता | 10 | 35 | 52 | 61 | 38 | 29 |
यहाँ पर अधिकतम वर्ग बारंबारता 61 है तथा इस बारंबारता का संगत वर्ग 60−80 है। बहुलक वर्ग = 60−80
बहुलक वर्ग = 60−80
बहुलक वर्ग की निम्न सीमा (l) = 60
वर्ग-माप (h) = 20
बहुलक वर्ग की बारंबारता (f1) = 61
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 52
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 38
अब बहुलक 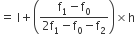
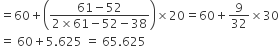
अत: दिए आँकड़ों के उपकरणों का बहुलक जीवनकाल 65.625 घंटे है।
निम्नलिखित आँकड़े किसी गाँव के 200 परिवारों के कुल मासिक घरेलू व्यय के बंटन को दर्शाते हैं। इन परिवारों का बहुलक मासिक व्यय ज्ञात कीजिए। साथ ही, माध्य मासिक व्यय भी ज्ञात कीजिए।
| व्यय रुपयों में | परिवारों की संख्या |
| 1000 - 1500 | 24 |
| 1500 - 2000 | 40 |
| 2000 - 2500 | 33 |
| 2500 - 3000 | 28 |
| 3000 - 3500 | 30 |
| 3500 - 4000 | 22 |
| 4000 - 4500 | 16 |
| 4500 - 5000 | 7 |
यहाँ पर अधिकतम वर्ग बारंबारता 40 है तथा इस बारंबारता का संगत वर्ग 1500 - 2000 है। बहुलक वर्ग = 1500 - 2000
बहुलक वर्ग = 1500 - 2000
बहुलक वर्ग की निम्न सीमा (l) = 1500
वर्ग-माप (h) = 500
बहुलक वर्ग की बारंबारता (f1) = 40
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 24
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 33
अब बहुलक = 
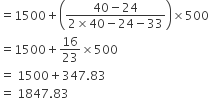
अत: परिवारों का बहुलक मासिक व्यय = ₹ 1847.83
माध्य मासिक व्यय के लिए -
माना कलिप्त माध्य (a) = 2750
वर्ग माप(h) = 500
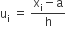
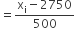
| वर्ग अंतराल | बारंबारता(fi) | वर्ग चिह्न (xi) | 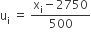 |
 |
| 1000-1500 | 24 | 1250 | -3 | -72 |
| 1500-2000 | 40 | 1750 | -2 | -80 |
| 2000-2500 | 33 | 2250 | -1 | -33 |
| 2500-3000 | 28 | 2750 | 0 | 0 |
| 3000-3500 | 30 | 3250 | 1 | 30 |
| 3500-4000 | 22 | 3750 | 2 | 44 |
| 4000-4500 | 16 | 4250 | 3 | 48 |
| 4500-5000 | 7 | 4750 | 4 | 28 |
| योग |  |
 |
अब माध्य
 =
= 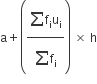
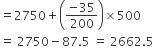
अत: परिवार का माध्य मासिक व्यय = ₹ 2662.5
निम्नलिखित बंटन भारत के उच्चतर माध्यमिक स्कूलों में, राज्यों के अनुसार, शिक्षक-विद्यार्थी अनुपात को दर्शाता है। इन आँकड़ों के बहुलक और माध्य ज्ञात कीजिए। दोनों मापकों की व्याख्या कीजिए।
| प्रति शिक्षक विद्यार्थियों की संख्या | राज्य/संघीय क्षेत्रों की संख्या |
| 15−20 | 3 |
| 20−25 | 8 |
| 25−30 | 9 |
| 30−35 | 10 |
| 35−40 | 3 |
| 40−45 | 0 |
| 45−50 | 0 |
| 50−55 | 2 |
यहाँ पर अधिकतम वर्ग बारंबारता 10 है तथा इस बारंबारता का संगत वर्ग 30−35 है।  बहुलक वर्ग = 30 - 35
बहुलक वर्ग = 30 - 35
बहुलक वर्ग की निम्न सीमा (l) = 30
वर्ग माप (h) = 5
बहुलक वर्ग की बारंबारता (f1) = 10
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 9
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 3
अब बहुलक 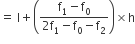
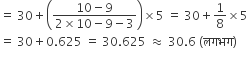
माध्य के लिए:
माना कलिप्त माध्य (a) = 32.5
वर्ग माप (h) = 5
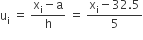
| वर्ग अंतराल | बारंबारता | वर्ग चिह्न (xi) | 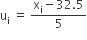 |
 |
| 15−20 | 3 | 17.5 | −3 | −9 |
| 20−25 | 8 | 22.5 | −2 | −16 |
| 25−30 | 9 | 27.5 | −1 | −9 |
| 30−35 | 10 | 32.5 | 0 | 0 |
| 35−40 | 3 | 37.5 | 1 | 3 |
| 40−45 | 0 | 42.5 | 2 | 0 |
| 45−50 | 0 | 47.5 | 3 | 0 |
| 50−55 | 2 | 52.5 | 4 | 8 |
| योग |  |
 |
माध्य
 =
= 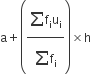
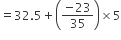
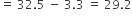
अत: अधिकांश राज्यों/U.T. में छात्र और अध्यापक का अनुपात 30.6 है तथा औसतन छात्र व अध्यापक अनुपात 29.2 है।
दिया हुआ बंटन विश्व के कुछ श्रेष्ठतम बल्लेबाज़ों द्वारा एकदिवसीय अंतर्राष्ट्रीय क्रिकेट मैचों में बनाए गए रनों को दर्शाता है:
| बनाए गए रन | बल्लेबाज़ों की संख्या |
| 3000−4000 | 4 |
| 4000−5000 | 18 |
| 5000−6000 | 9 |
| 6000−7000 | 7 |
| 7000−8000 | 6 |
| 8000−9000 | 3 |
| 9000−10000 | 1 |
| 10,000 −11,000 | 1 |
यहाँ पर अधिकतम वर्ग बारंबारता 18 है तथा इस बारंबारता का संगत वर्ग 4000−5000 है। बहुलक वर्ग = 4000−5000
बहुलक वर्ग = 4000−5000
बहुलक वर्ग की निम्न सिमा (l) = 4000
वर्ग माप (h) = 1000
बहुलक वर्ग की बारंबारता (f1) = 18
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 4
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 9
अब बहुलक = 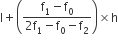
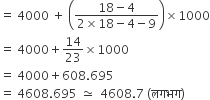
अत: दिए गए आँकड़ों का बहुलक = 4608.7 (लगभग)
एक विद्यार्थी ने एक सड़क के किसी स्थान से होकर जाती हुई कारों की संख्याएँ नोट की और उन्हें नीचे दी हुई सारणी के रूप में व्यक्त किया। सारणी में दिया प्रत्येक प्रेक्षण 3 मिनट के अंतराल में उस स्थान से होकर जाने वाली कारों की संख्याओं से सम्बंधित है। ऐसे 100 अंतरालों पर प्रेक्षण लिए गए। इन आँकड़ों का बहुलक ज्ञात कीजिए।
| कारों की संख्या | 0−10 | 10−20 | 20−30 | 30−40 | 40−50 | 50−60 | 60−70 | 70−80 |
| बारंबारता | 7 | 14 | 13 | 12 | 20 | 11 | 15 | 8 |
यहाँ पर अधिकतम वर्ग बारंबारता है तथा इस बारंबारता का संगत वर्ग 40−50 है। बहुलक वर्ग = 40−50
बहुलक वर्ग = 40−50
बहुलक वर्ग की निम्न संख्या (l) = 40
वर्ग-माप (h) = 10
बहुलक वर्ग की बारंबारता (f1) = 20
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 12
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 11
अब बहुलक = 
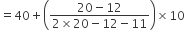
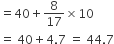
अत: दिए गए आँकड़ों का बहुलक = 44.7 कारें
निम्नलिखित बारंबारता बंटन किसी मोहल्ले के 68 उपभोक्ताओं की बिजली की मासिक खपत दर्शाता है। इन आँकड़ों के माध्यक, माध्य और बहुलक ज्ञात कीजिए। इनकी तुलना कीजिए।
| मासिक खपत (इकाइयों में) | उपभोक्ताओं की संख्या |
| 65−85 | 4 |
| 85−105 | 5 |
| 105−125 | 13 |
| 125−145 | 20 |
| 145−165 | 14 |
| 165−185 | 8 |
| 185−205 | 4 |
माध्यक के लिए -
| मासिक खपत (इकाइयों में) | उपभोक्ताओं की संख्या(f) | संचयी बारंबारता (cf) |
| 65−85 | 4 | 4 |
| 85−105 | 5 | 9 |
| 105−125 | 13 | 22 |
| 125−145 | 20 | 42 |
| 145−165 | 14 | 56 |
| 165−185 | 8 | 64 |
| 185−205 | 4 | 68 |
| योग | n = 68 |
यहाँ पर n = 68
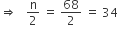 जो की वर्ग अंतराल 125−145 में आता है।
जो की वर्ग अंतराल 125−145 में आता है। अत: माध्यक वर्ग = 125−145
माध्यक वर्ग की निम्न सीमा (l) = 125
वर्ग माप (h) = 20
माध्यक वर्ग के ठीक पहले वर्ग की संचयी बारंबारता (cf) = 22
माध्यक वर्ग की बारंबारता (f) = 20
अब माध्यक =
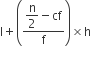
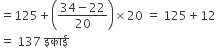
माध्य के लिए-
माना कलिप्त माध्य (a) = 135
वर्ग माप (h) = 20

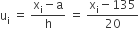
| वर्ग-अंतराल | बारंबारता (fi) | वर्ग चिह्न (xi) | 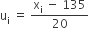 |
 |
| 65−85 | 4 | 75 | −3 | −12 |
| 85−105 | 5 | 95 | −2 | −10 |
| 105−125 | 13 | 115 | −1 | −13 |
| 125−145 | 20 | 135 | 0 | 0 |
| 145−165 | 14 | 155 | 1 | 14 |
| 165−183 | 8 | 175 | 2 | 16 |
| 183−205 | 4 | 195 | 3 | 12 |
| योग |  |
 |
अब माध्य
 =
= 

बहुलक के लिए - यहाँ पर अधिकतम वर्ग बारंबारता 20 है तथा इस बारंबारता का संगत वर्ग 125−145 है।
 बहुलक वर्ग = 125−145
बहुलक वर्ग = 125−145बहुलक वर्ग की निम्न सीमा (l) = 125
वर्ग माप (h) = 20
बहुलक वर्ग की बारंबारता (f1) = 20
बहुलक वर्ग से ठीक पहले वाले वर्ग की बारंबारता (f0) = 13
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 14
बहुलक =
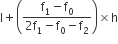
=
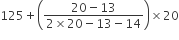
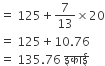
यहाँ पर दिए गए आँकड़ों के लिए तीनों मापक लगभग समान हैं।
यदि नीचे दिए हुए बंटन का माध्यक 28.5 हो तो x और y के मान ज्ञात कीजिए:
| वर्ग अंतराल | बारंबारता |
| 0−10 | 5 |
| 10−20 | x |
| 20−30 | 20 |
| 30−40 | 15 |
| 40−50 | y |
| 50−60 | 5 |
| योग | 60 |
यहाँ पर दिया गया है - माध्यक = 28.5; n = 60
| वर्ग अंतराल | बारंबारता (f) | संचयी बारंबारता (cf) |
| 0−10 | 5 | 5 |
| 10−20 | x | 5 + x |
| 20−30 | 20 | 25 + x |
| 30−40 | 15 | 40 + x |
| 40−50 | y | 40 + x + y |
| 50−60 | 5 | 45 + x + y |
| योग | n = 60 |
क्योंकि माध्यक 28.5 दिया है इसलिए माध्यक वर्ग = 20−30
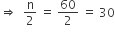
माध्यक वर्ग की निम्न सीमा (l) = 20
वर्ग माप (h) = 10
माध्यक वर्ग के ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 5 + x
माध्यक वर्ग की बारंबारता (f) = 20
हमे जानते हैं कि माध्यक =
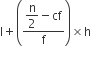

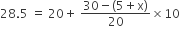

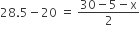
 8.5 x 2 = 25 − x
8.5 x 2 = 25 − x x = 25−17 = 8
x = 25−17 = 8अब 45 + x + y = 60
 45 + 8 + y = 60
45 + 8 + y = 60 y = 60−53
y = 60−53= 7
Sponsor Area
एक जीवन बीमा एजेंट 100 पॉलिसी धारकों की आयु के बंटन के निम्नलिखित आँकड़े ज्ञात करता है। माध्यक आयु परिकलित कीजिए, यदि पॉलिसी केवल उन्ही व्यक्तियों को दी जाती है, जिनकी आयु 18 वर्ष या उससे अधिक हो, परन्तु 60 वर्ष से कम हो।
| आयु (वर्षों में) | पॉलिसी धारकों की संख्या |
| 20 से कम | 2 |
| 25 से कम | 6 |
| 30 से कम | 24 |
| 35 से कम | 45 |
| 40 से कम | 78 |
| 45 से कम | 89 |
| 50 से कम | 92 |
| 55 से कम | 98 |
| 60 से कम | 100 |
| आयु (वर्षों में) | बारंबारता (f) | संचयी बारंबारता (cf) |
| 15−20 | 2 | 2 |
| 20−25 | 4 | 6 |
| 25−30 | 18 | 24 |
| 30−35 | 21 | 45 |
| 35−40 | 33 | 78 |
| 40−45 | 11 | 89 |
| 45−50 | 3 | 92 |
| 50−60 | 6 | 98 |
| 55−60 | 2 | 100 |
| योग | n = 100 |
यहाँ पर, n = 100
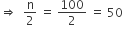 जो वर्ग-अंतराल 35−40 में आता है।
जो वर्ग-अंतराल 35−40 में आता है। अत: अत:माध्यक वर्ग = 35−40
अब माध्यक वर्ग की निम्न सीमा (l) = 35
वर्ग-माप (h) = 5
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 45
माध्यक वर्ग की बारंबारता (f) = 33
माध्यक =
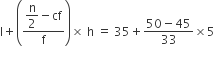
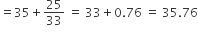
अत: माध्यक आयु = 35.76 वर्ष
एक पौधे की 40 पत्तियों की लंबाइयाँ निकटतम मिलीमीटरों में मापी जाती हैं तथा प्राप्त आँकड़ों को निम्नलिखित सारणी के रूप में निरूपित किया जाता है:
| लंबाई (mm में) | पत्तियों की संख्या |
| 118−126 | 3 |
| 127−135 | 5 |
| 136−144 | 9 |
| 145−153 | 12 |
| 154−162 | 5 |
| 163−171 | 4 |
| 172−180 | 2 |
यहाँ पर माध्यक ज्ञात करने के लिए, आँकड़ों को सतत वर्ग अंतरालों में बदलना पड़ेगा, क्योंकि सूत्र में वर्ग अंतरालों को सतत माना गया है, जो निम्नलिखित होंगे:
| लंबाई (mm में) | पत्तियों की संख्या (बारंबारता) (f) | संचयी बारंबारता (cf) |
| 117.5−126.5 | 3 | 3 |
| 126.5−135.5 | 5 | 8 |
| 135.5−144.5 | 9 | 17 |
| 144.5−153.5 | 12 | 29 |
| 153.5−162.5 | 5 | 34 |
| 162.5−171.5 | 4 | 38 |
| 171.5−180.5 | 2 | 40 |
| योग | n = 40 |
n = 40

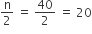 जो की वर्ग-अंतराल 144.5−153.5 में आता है।
जो की वर्ग-अंतराल 144.5−153.5 में आता है। अत: माध्यक वर्ग = 144.5−153.5
अब माध्यक वर्ग की निम्न सीमा (l) = 144.5
वर्ग-माप (h) = 9
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 17
माध्यक वर्ग की बारंबारता (f) = 12
माध्यक =
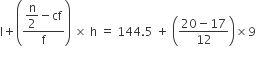
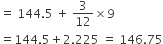
अत: पत्तियों की माध्यक लम्बाई = 146.75 mm
निम्नलिखित सारणी 400 नियॉन लैम्पों के जीवनकालों (life time) को प्रदर्शित करती है:
| जीवन काल (घंटों में) | लैम्पों की संख्या |
| 1500 - 2000 | 14 |
| 2000 - 2500 | 56 |
| 2500 - 3000 | 60 |
| 3000 - 3500 | 86 |
| 3500 - 4000 | 74 |
| 4000 - 4500 | 62 |
| 4500 - 5000 | 48 |
एक लैंप का माध्यक जीवनकाल ज्ञात कीजिए।
| जीवनकाल (घंटों में) | लैम्पों की संख्या (f) | संचयी बारंबारता (cf) |
| 1500 - 2000 | 14 | 14 |
| 2000 - 2500 | 56 | 70 |
| 2500 - 3000 | 60 | 130 |
| 3000 - 3500 | 86 | 216 |
| 3500 - 4000 | 74 | 290 |
| 4000 - 4500 | 62 | 352 |
| 4500 - 5000 | 48 | 400 |
| योग | n = 400 |
यहाँ पर n = 400

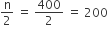 जो कि वर्ग-अंतराल 3000 - 3500 में आता है।
जो कि वर्ग-अंतराल 3000 - 3500 में आता है।अत: माध्यक वर्ग = 3000 - 3500
अब माध्यक वर्ग की निम्न सीमा (l) = 3000
वर्ग-माप (h) = 500
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 130
माध्यक वर्ग की बारंबारता (f) = 86
माध्यक =
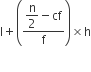
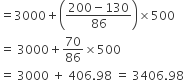
अतः दिए गए लैम्पों का माध्यक जीवनकाल = 3406.98 घण्टे
एक स्थानीय टेलीफ़ोन निर्देशिका से कुलनाम लिए गए और उनमें प्रयुक्त अंग्रेज़ी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारंबारता बंटन प्राप्त हुआ:
| अक्षरों की संख्या | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| कुलनामों की संख्या | 6 | 30 | 40 | 16 | 4 | 4 |
| अक्षरों की संख्या | कुलनामों की संख्या बारंबारता (f) | संचयी बारंबारता (cf) |
| 1−4 | 6 | 6 |
| 4−7 | 30 | 36 |
| 7−10 | 40 | 76 |
| 10−13 | 16 | 92 |
| 13−16 | 4 | 96 |
| 16−19 | 4 | 100 |
| योग | n = 100 |
यहाँ पर n = 100

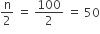 जो कि वर्ग-अंतराल 7−10 में आता है।
जो कि वर्ग-अंतराल 7−10 में आता है।अत: माध्यक वर्ग = 7−10
अब माध्यक वर्ग की निम्न सीमा (l) = 7
वर्ग माप (h) = 3
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 36
माध्यक वर्ग की बारंबारता (f) = 40
माध्यक =
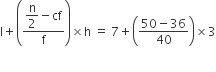
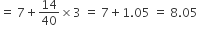
∴ माध्य
 =
= 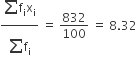
बहुलक के लिए - यहाँ पर अधिकतम वर्ग बारंबारता 40 है तथा इस बारंबारता का संगत वर्ग 7−10 है।
 बहुलक वर्ग = 7−10
बहुलक वर्ग = 7−10बहुलक वर्ग की निम्न सीमा (l) = 7
वर्ग माप (h) = 3
बहुलक वर्ग की बारंबारता (f1) = 40
बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता (f0) = 30
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 16
बहुलक =
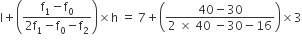
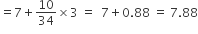
अतः माध्यक = 8.05, माध्य = 8.32 व बहुलक = 7.88
नीचे दिया हुआ बंटन एक कक्षा के 30 विद्यार्थियों के भार दर्शा रहा है। विद्यार्थियों का माध्यक भार ज्ञात कीजिए।
| भार (किलोग्राम में) | 40-45 | 45-50 | 50-55 | 55-60 | 60-65 | 65-70 | 70-75 |
| विद्यार्थियों की संख्या | 2 | 3 | 8 | 6 | 6 | 3 | 2 |
| भार (किलोग्राम में) | विद्यार्थियों की संख्या (बारंबारता) (f) | संचयी बारंबारता (cf) |
| 40 - 45 | 2 | 2 |
| 45 - 50 | 3 | 5 |
| 50 - 55 | 8 | 13 |
| 55 - 60 | 6 | 19 |
| 60 - 65 | 6 | 25 |
| 65 - 70 | 3 | 28 |
| 70 - 75 | 2 | 30 |
| योग | n = 30 |
यहाँ पर n = 30
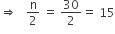 जो कि वर्ग-अंतराल 55−60 में आता है।
जो कि वर्ग-अंतराल 55−60 में आता है। अत: माध्यक वर्ग = 55−60
अब माध्यक वर्ग कि निम्न सीमा (l) = 55
वर्ग-माप (h) = 5
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 13
माध्यक वर्ग की बारंबारता (f) = 6
माध्यक
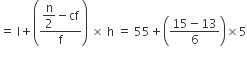
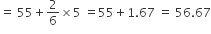
अत: विद्यार्थियों का माध्यक भार = 56.67 किलोग्राम
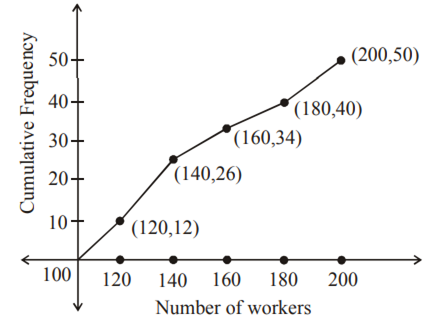
निम्नलिखित बंटन किसी फैक्ट्री के श्रमिकों की दैनिक आय दर्शाता है:
'उपरोक्त बंटन को एक कम प्रकार' के संचयी बारंबारता बंटन में बदलिए और उसका तोरण खींचिए।
दी गई बारंबारता बंटन को एक कम प्रकार की संचयी बारंबारता बंटन सारणी में बदलने पर प्राप्त होगा-
| दैनिक आय (रुपयों में) | संचयी बारंबारता |
| 120 से कम | 12 |
| 140 से कम | 26 (14+12) |
| 160 से कम | 34 (26+8) |
| 180 से कम | 40 (34+6) |
| 200 से कम | 50 (40+10) |
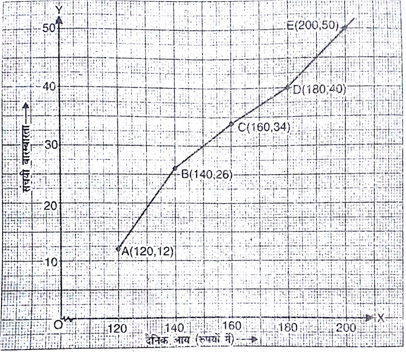
किसी कक्षा के 35 विद्यार्थियों की मेडिकल जांच के समय, उनके भार निम्नलिखित रूप में रिकॉर्ड किए गए: 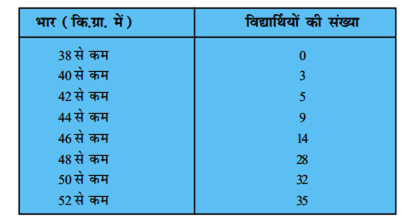
उपरोक्त आँकड़ों के 'लिए कम प्रकार का तोरण' खींचिए। इसके बाद माध्यक भार ज्ञात कीजिए।
बिंदुओं A(38, 0), B(40, 3), C(42, 5), D(44, 9), E(46, 14), F(48, 28), G(50, 32) व H(52, 35) को ग्राफ पेपर पर अंकित कर इन्हें मुक्त हाथ से मिलाकर कम प्रकार का तोरण प्राप्त कीजिए। 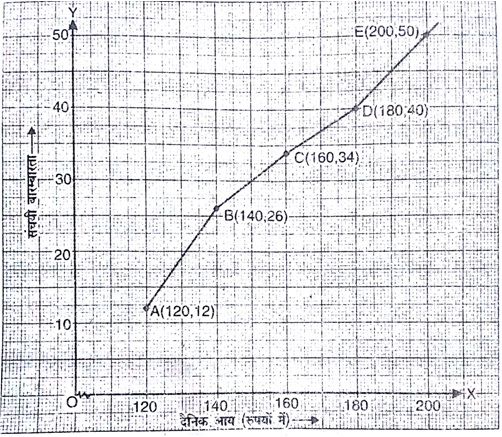
ग्राफ पेपर पर 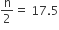 के विरुद्ध x निर्देशांक 47 प्राप्त होता है। इसलिए दी गई सारणी का माध्यक 47 है।
के विरुद्ध x निर्देशांक 47 प्राप्त होता है। इसलिए दी गई सारणी का माध्यक 47 है।
निम्नलिखित सारणी किसी गाँव के 100 फार्मों में हुआ प्रति हेक्टेयर(ha) गेहूँ का उत्पादन दर्शाते हैं:
इस बंटन को 'अधिक के प्रकार के' बंटन में बदलिए और फिर उनका तोरण खींचिए।
दी गई बारंबारता सारणी से अधिक के प्रकार के बंटन की सारणी होगी:
| उत्पादन (kg/ha) | संचयी बारंबारता |
| 50 के बराबर या अधिक | 100 |
| 55 के बराबर या अधिक | 98 |
| 60 के बराबर या अधिक | 90 |
| 65 के बराबर या अधिक | 78 |
| 70 के बराबर या अधिक | 54 |
| 75 के बराबर या अधिक | 16 |
अब हम ग्राफ पेपर पर बिंदुओं A(50, 100), B(55, 98), C(60, 90), D(65, 78), E(70, 54) और F(75, 16) की आलेखित कर निम्न तोरण प्राप्त होते हैं। 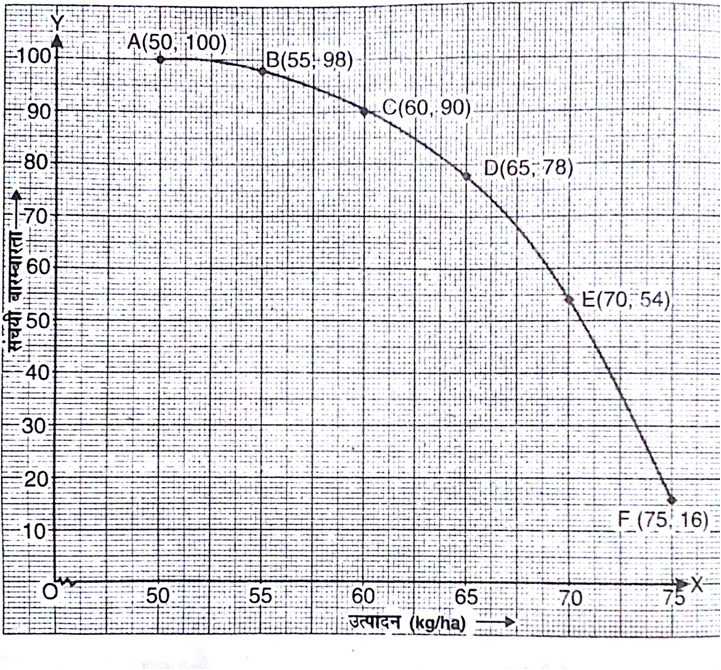
नीचे दी गई तालिका में 280 व्यक्तियों के वेतन दिखाए गए हैं
| वेतन हजार में | व्यक्तियों की संख्या |
| 5-10 | 49 |
| 10-15 | 133 |
| 15-20 | 63 |
| 20-25 | 15 |
| 25-30 | 6 |
| 30-35 | 7 |
| 35-40 | 4 |
| 40-45 | 2 |
| 45-50 | 1 |
डेटा के औसत वेतन की गणना करें।
| वेतन हजार में | व्यक्तियों की संख्या (F) | Cumulative Frequency (f) |
| 5 -10 | 49 | 49 |
| 10-15 | 133 | 182 |
| 15-20 | 63 | 245 |
| 20-25 | 15 | 260 |
| 25-30 | 6 | 266 |
| 30-35 | 7 | 273 |
| 35-40 | 4 | 277 |
| 40-45 | 2 | 279 |
| 45-50 | 1 | 280 |
निम्न बंटन का माध्य 18 है वर्ग की बारंबारता f ज्ञात कीजिए
| वर्ग | 11-13 | 13-15 | 15-17 | 17-19 | 19-21 | 21-23 | 23-25 |
| बारंबारता | 3 | 6 | 9 | 13 | f | 5 | 4 |
| Class | Mid values xi | Frequency fi | di = xi -18 | fiui | |
| 11-13 | 12 | 3 | -6 | -3 | 9 |
| 13-15 | 14 | 6 | -4 | -2 | -12 |
| 15-17 | 16 | 9 | -2 | -1 | -9 |
| 17-19 | 18 | 13 | 0 | 0 | 0 |
| 19-21 | 20 | f | 2 | 1 | f |
| 21-23 | 22 | 5 | 4 | 2 | 10 |
| 23-25 | 24 | 4 | 6 | 3 | 12 |
| Σfi = 40 +f |
निम्न बंटन किसी फैक्ट्री के 50 कर्मचारियों की दैनिक आय दर्शाता है :
| दैनिक आय | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| कर्मचारियों की संख्या | 12 | 14 | 8 | 6 | 10 |
उपरोक्त बंटन को एक क्रम प्रकार के संचयी बारंबारता बंटन में बदलिए उसका तोरण खींचिए।
| Daily income | Frequency | Income less than | cumulative frequency |
| 100-120 | 12 | 120 | 12 |
| 120-140 | 14 | 140 | 26 |
| 140-160 | 8 | 160 | 34 |
| 160-180 | 6 | 180 | 40 |
| 180-200 | 10 | 200 | 50 |
Mock Test Series
Sponsor Area
Sponsor Area