Question
एक स्थानीय टेलीफ़ोन निर्देशिका से कुलनाम लिए गए और उनमें प्रयुक्त अंग्रेज़ी वर्णमाला के अक्षरों की संख्या का निम्नलिखित बारंबारता बंटन प्राप्त हुआ:
| अक्षरों की संख्या | 1-4 | 4-7 | 7-10 | 10-13 | 13-16 | 16-19 |
| कुलनामों की संख्या | 6 | 30 | 40 | 16 | 4 | 4 |
Solution
माध्यक के लिए:
यहाँ पर n = 100

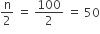 जो कि वर्ग-अंतराल 7−10 में आता है।
जो कि वर्ग-अंतराल 7−10 में आता है।
अत: माध्यक वर्ग = 7−10
अब माध्यक वर्ग की निम्न सीमा (l) = 7
वर्ग माप (h) = 3
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 36
माध्यक वर्ग की बारंबारता (f) = 40
माध्यक =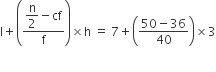
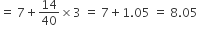
∴ माध्य =
= 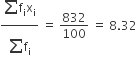
बहुलक के लिए - यहाँ पर अधिकतम वर्ग बारंबारता 40 है तथा इस बारंबारता का संगत वर्ग 7−10 है।
 बहुलक वर्ग = 7−10
बहुलक वर्ग = 7−10
बहुलक वर्ग की निम्न सीमा (l) = 7
वर्ग माप (h) = 3
बहुलक वर्ग की बारंबारता (f1) = 40
बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता (f0) = 30
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 16
बहुलक =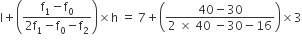
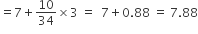
अतः माध्यक = 8.05, माध्य = 8.32 व बहुलक = 7.88
| अक्षरों की संख्या | कुलनामों की संख्या बारंबारता (f) | संचयी बारंबारता (cf) |
| 1−4 | 6 | 6 |
| 4−7 | 30 | 36 |
| 7−10 | 40 | 76 |
| 10−13 | 16 | 92 |
| 13−16 | 4 | 96 |
| 16−19 | 4 | 100 |
| योग | n = 100 |
यहाँ पर n = 100

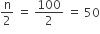 जो कि वर्ग-अंतराल 7−10 में आता है।
जो कि वर्ग-अंतराल 7−10 में आता है।अत: माध्यक वर्ग = 7−10
अब माध्यक वर्ग की निम्न सीमा (l) = 7
वर्ग माप (h) = 3
माध्यक वर्ग से ठीक पहले वाले वर्ग की संचयी बारंबारता (cf) = 36
माध्यक वर्ग की बारंबारता (f) = 40
माध्यक =
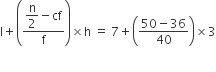
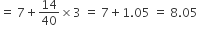
∴ माध्य
 =
= 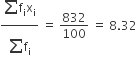
बहुलक के लिए - यहाँ पर अधिकतम वर्ग बारंबारता 40 है तथा इस बारंबारता का संगत वर्ग 7−10 है।
 बहुलक वर्ग = 7−10
बहुलक वर्ग = 7−10बहुलक वर्ग की निम्न सीमा (l) = 7
वर्ग माप (h) = 3
बहुलक वर्ग की बारंबारता (f1) = 40
बहुलक वर्ग से ठीक पहले वर्ग की बारंबारता (f0) = 30
बहुलक वर्ग के ठीक बाद में आने वाले वर्ग की बारंबारता (f2) = 16
बहुलक =
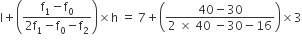
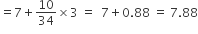
अतः माध्यक = 8.05, माध्य = 8.32 व बहुलक = 7.88



