Mathematics Chapter 11 Constructions
Sponsor Area
NCERT Solution For Class 9 About 2.html
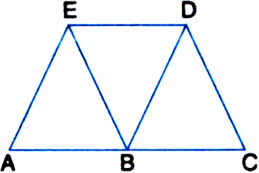
Which of the following figures lie on the same base and between the same parallels. In such a case, write the common base and the two parallels.
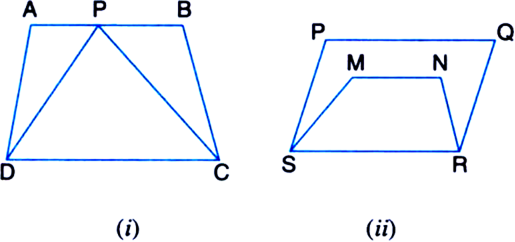
(i) ΔPDC and quadrilateral ABCD lie on the same base DC and between the same parallels DC and AB.
(iii) ΔTRQ and parallelogram SRQP lie on the same base RQ and between the same parallels RQ and SP.
(v) Quadrilaterals APCD and ABQD lie on the same base AD and between the same parallels AD and BQ.
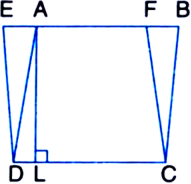
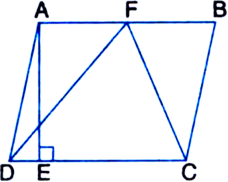
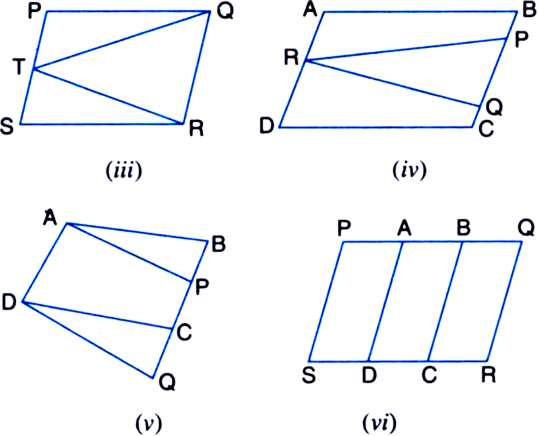
In figure, ABCD is a parallelogram, AE ⊥ DC and CF ⊥ AD. If AB = 16 cm, AE = 8 cm and CF = 10 cm, find AD.
ar(parallelogram ABCD) = AB x AE = 16 x 8 cm2
= 128 cm2 ...(1)
ar(parallelogram ABCD) = AD x CF
= AD x 10 cm2 ...(2)
From (1) and (2), we get
AD X 10 = 128![]()
![]() ad = 12.8 cm
ad = 12.8 cm
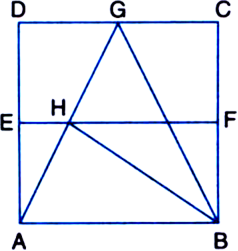
If E, F, G and H are respectively the mid-points of the sides of a parallelogram ABCD, show that ar(EFGH) = ![]() ar(ABCD).
ar(ABCD).
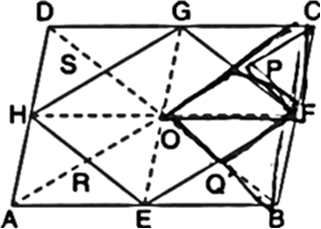
To Prove: ar(EFGH) =
ar(ABCD).
Construction: Join OF, OG, OH and OE. Also, join AC and BD.
Proof: In ΔBCD,
∵ F and G are the mid-points of BC and DC respectively.
∴ FG || BD ...(1)
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side
In ΔBAD,
∵ E and H are the mid-points of AB and AD respectively.
EH || BD ...(2)
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side
From (1) and (2),
EH || FG ...(3)
Similarly, we can prove that
EF || HG ...(4)
From (3) and (4),
Quadrilateral EFGH is a parallelogram
| A quadrilateral is a parallelogram if its opposite sides are equal
∵ F is the mid-point of CB and O is the mid-point of CA
FO || BA
In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side and is half of it ⇒ FO || CG ...(5)
V BA || CD (opposite sides of a parallelogram are parallel)
∴ BA || CG
and 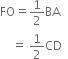
∵ Opposite sides of a parallelogram are equal = CG ...(6)
| ∵ G is the mid-point of CD In view of (5) and (6),
Quadrilateral OFCG is a parallelogram
∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel and are of
equal length
∵ OP = PC
| ∵ Diagonals of a || gm bisect each other
∵ ΔOPF and ∵CPF have equal bases
(∵ OP = PC) and have a common vertex F Their altitudes are also the same ar(ΔOPF) = ar(ΔCPF)
Similarly, ar(ΔOQF) = ar(ΔBQF)
Adding, we get
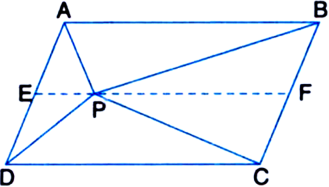
ar(ΔOPF) + ar(ΔOQF) = ar(ΔCPF) + ar(ΔBQF) ⇒ ar(|| gm OQFP) = ar(ΔCPF) + ar(ΔBQF) ....(7)
Similarly,
ar(|| gm OPGS) = ar(⇒GPC) + ar(⇒DSG) ...(8)
ar(|| gm OSHR) = ar(ΔDSH) + ar(ΔHAR)
ar(|| gm OREQ) = ar(ΔARE) + ar(ΔEQB) ...(10)
Adding the corresponding sides of (7), (8), (9) and (10), we get
ar(|| gm EFGH) = {ar(ACPF} + ar(ΔGPC)}
+ {ar(ΔDSG) + ar(ΔDSH)} + {ar(ΔHAR) + ar(ΔARE)} + (ar(ΔBQF) + ar(ΔEQB)}
= ar(ΔFCG) + ar(ΔGDH) + ar(ΔHAE) + ar(ΔEBF)
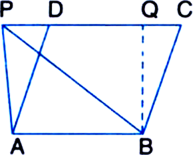
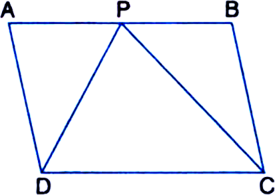
P and Q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(ΔAPB) = ar{ΔBQC).
To Prove: ar(ΔAPB) = ar(ΔBQC).
Proof: ∵ ΔAPB and || gm ABCD are on the same base AB and between the same parallels AB and DC.
∵ ΔBQC and || gm ABCD are on the same base BC and between the same parallels BC and AD.
From (1) and (2),
ar(ΔAPB) = ar(ΔBQC).
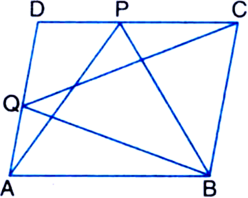
In figure, P is a point in the interior of a parallelogram ABCD. Show that:
(1) ar(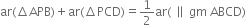
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD). [CBSE 2012 (March)]
[Hint. Through P, draw a line parallel to AB.]
To Prove : (i)
ar(|| gm ABCD)
(ii) ar(ΔAPD) + ar(ΔPBC) = ar(ΔAPB) + ar(ΔPCD).
Construction: Through P, draw a line EF parallel to AB.
Proof: (i) EF || AB ...(1) | by construction
∵ AD || BC
∵ Opposite sides of a parallelogram are parallel
∴ AE || BF ...(2)
In view of (1) and (2),
Quadrilateral ABFE is a parallelogram
A quadrilateral is a parallelogram if its opposite sides are parallel
Similarly, quadrilateral CDEF is a parallelogram
∵ ΔAPB and || gm ABFE are on the same base AB and between the same parallels AB and EF.
∵ ΔPCD and || gm CDEF are on the same base DC and between the same parallels DC and EF.
Adding (3) and (4), we get ar(ΔAPB) + ar(ΔPCD)
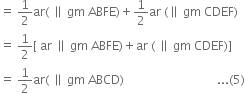
(ii) ar(ΔAPD) + ar(ΔPBC)
= ar(|| gm ABCD) – [ar(ΔAPB) + ar(ΔPCD)] = 2 [ar(ΔAPB) + ar(ΔPCB)] – [ar(ΔAPB) + ar(ΔPCD)]
= ar(ΔAPB) + ar(ΔPCD).
In figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that: 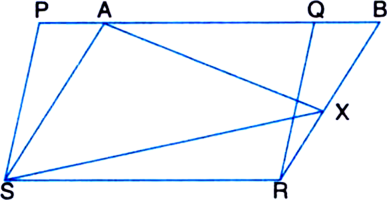
(i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
Given: PQRS and ABRS are parallelograms and X is any point on side BR.
To Prove: (i) ar(|| gm PQRS) = ar(|| gm ABRS)
(ii) ![]()
Proof: (i) In ΔPSA and ΔQRB,
∠SPA = ∠RQB ...(1)
Corresponding angles from PS || QR and transversal PB
∠PAS = ∠QBR ...(2)
Corresponding angles from AS || BR and transversal PB
∠PSA = ∠QRB ...(3)
| Angle sum property of a triangle Also, PS = QR ...(4)
| Opposite sides of || gm PQRS In view of (1), (3) and (4),
ΔPSA ≅ ΔQRB ...(5)
| By ASA Rule ∴ ar(ΔPSA) = ar(ΔQRB) ...(6)
| ∴ Congruent figures have equal areas Now, ar(|| gm PQRS) = ar(ΔPSA)
+ ar(|| gm AQRS) = ar(ΔQRB) + ar(|| gm AQRS)
| Using (6)
= ar(|| gm ABRS)
(ii) ∵ ΔAXS and || gm ABRS are on the same base AS and between the same parallels AS and BR.
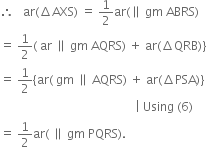
A farmer was having a field in the form of a parallelogram PQRS. She took any point A on RS and joined it to points P and Q. In how many parts the fields is divided? What are the shapes of these parts? The farmer wants to sow wheat and pulses in equal portions of the field separately. How should she do it?
∴ Their altitudes are same. Let it be x. Then,
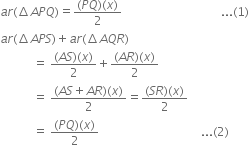
∵ SR = PQ (opposite sides of parallelogram are equal)
Therefore, either the farmer should sow wheat in ΔAPQ and pulses in the other two triangles APS and AQR or pulses in ΔAPQ and wheat in the other two triangles APS and AQR.
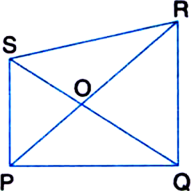
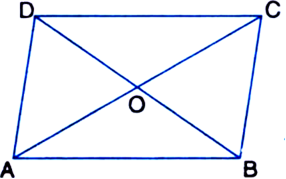
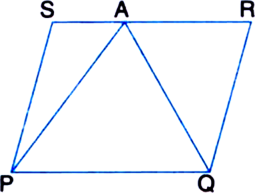
The diagonals of a parallelogram ABCD intersect at a point O. Through O, a line is drawn to intersect AD at P and BC at Q. Show that PQ divides the parallelogram into two parts of equal area.
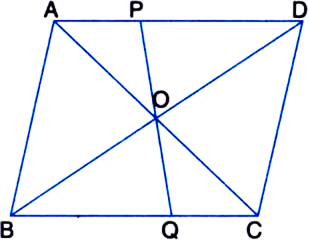
To Prove: ar(□PDCQ) = ar(□PQBA). Proof: ∵ AC is a diagonal of || gm ABCD ∴ ar(ΔABC) = ar(ΔACD)
In ΔAOP and ΔCOQ,
AO = CO
| ∵ Diagonals of a parallelogram bisect each other
∠AOP = ∠COQ
| Vertically opposite angles ∠OAP = ∠OCQ
| Alternate interior angles ∴ ΔAOP = ΔCOQ
| By ASA Congruence Rule ∴ ar(ΔAOP) = ar(ΔCOQ)
| ∵ Congruent figures have equal areas ⇒ ar(ΔAOP) + ar(□OPDC)
= ar(ΔCOQ) + ar(□OPDC)
⇒ ar(ΔACD) = ar(□PDCQ)
⇒ 1/2 ar(|| gm ABCD) = ar(□PDCQ)
| From (1) ⇒ ar(□PQBA) = ar(□PDCQ)
⇒ ar(□PDCQ) = ar(□PQBA).
Prove that of all parallelograms of which the sides are given, the parallelogram which is a rectangle, has the greatest area.
Given: A parallelogram ABCD whose sides are given.
To Prove: The area of the parallelogram ABCD is the greatest when it is a rectangle.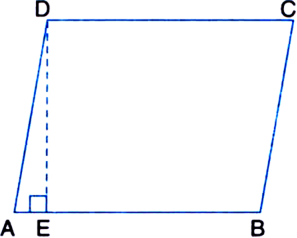
Construction: Draw DE ⊥ AB.
Proof: ar(|| gm ABCD)
= Base x Corresponding altitude = AB x DE
When parallelogram ABCD is a rectangle, then its area = AB x DA
| ∵ Then ∠DAB = 90° as such DA will be the altitude
In right triangle DEA,
∠DEA > ∠DAE
DA > DE
∵ Side opposite to greater angle of a triangle is longer ∴ ar(rectangle ABCD) > ar(|| gm ABCD)
i.e., the area of the parallelogram ABCD is the greatest when it is a rectangle.
In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).
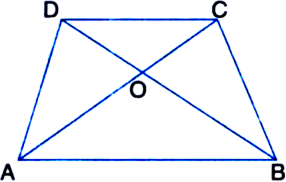
Given: Diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O.
To Prove: ar(ΔAOD) = ar(ΔBOC)
Proof: ∵ ΔADB and ΔACB are on the same base AB and between the same parallels AB and DC ∴ ar(ΔADB) = ar(ΔACB)
∵ Two triangles on the same base and between the same parallels are equal in area ⇒ ar(ΔADB) – ar(ΔAOB)
= ar(ΔACB) – ar(ΔAOB)
| Subtracting ar(ΔAOB) from both sides Δ ar(ΔAOD) = ar(ΔBOC)
Parallelograms on the same base and between same parallels are equal in area. Prove this.
Given: Two parallelograms ABCD and EFCD, on the same base DC and between the same parallels AF and DC.
To Prove: ar(ABCD) = ar(EFCD)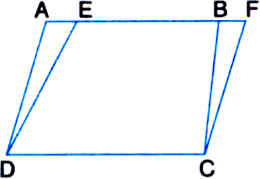
Proof: In ΔADE and ΔBCF,
∠DAE = ∠CBF ...(1)
Corresponding angles
(∵ AD || BC and a transversal AF intersects them)
∠AED = ∠BFC ...(2)
Corresponding angles (∵ ED || FC and a transversal AF intersects them)
∴ ∠ADE = ∠BCF ...(3)
| Angle sum property of a triangle Also AD = BC ...(4)
Opposite sides of the parallelogram ABCD
∴ ΔADE ≅ ΔBCF | By ASA congruence rule, using (1), (3) and (4) ∴ ar(ΔADE) = ar(ΔBCF)
| ∵ Congruent figures have equal areas ⇒ ar(ΔADE) + ar(EDCB)
= ar(ΔBCF) + ar(EDCB)
| Adding ar(EDCB) to both sides ⇒ ar(ABCD) = ar(EFCD)
So, parallelograms ABCD and EFCD are equal in area.
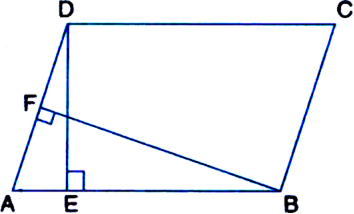
In figure, AD is median of triangle ABC, E is the mid-point of AD and F is the mid-point of AE.
Prove that 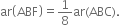
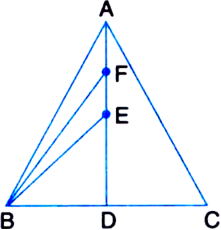
Proof :
V A median of a triangle divides it into two triangles of equal areas
∵ E is the mid-point of AD
∴ BE is a median of ΔABD
∴ ar(ΔBED) = ar(ΔBEA) = 1/2 ar(ΔABD)
∵ A median of a triangle divides it into two triangles of equal areas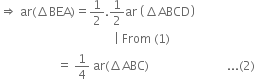
∵ F is the mid-point of AE ∴ BF is a median of ΔABE![]()
[ ![]() A median of a triangle divides it into two triangles of equal areas]
A median of a triangle divides it into two triangles of equal areas]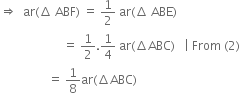
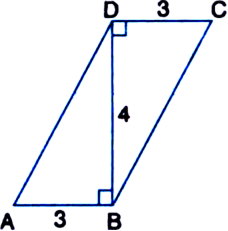
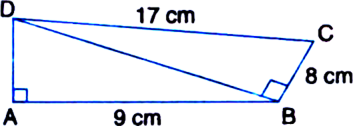
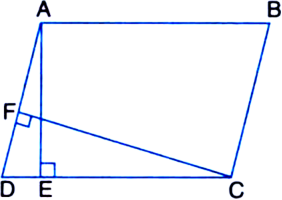
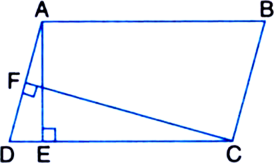
ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

Given: ABCD is a quadrilateral and BD is one of its diagonals.
To Prove: ABCD is a parallelogram and to determine its area.
Proof: ∠ABD = ∠BDC (= 90°) | Given But these angles form a pair of equal alternate
interior angles for lines AB, DC and a transversal BD AB || DC
Also, AD = DC (= 3 cm) | Given
Hence, quadrilateral ABCD is a parallelogram. A quadrilateral is a parallelogram if its one pair of opposite sides are parallel and equal Now,
ar(||gm ABCD) = Base x corresponding altitude
= 3x4 = 12 cm2
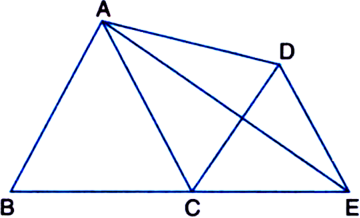
In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).
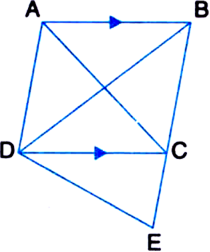
Given: AB || DC in the given figure.
To Prove: ar(BDE) = ar(ACED)
Proof: ∵ ΔADC and ΔBDC are on the same base DC and between the same parallels AB and DC ∴ ar(ΔADC) = ar(ΔBDC)
⇒ ar(ΔADC) + ar(ΔDCE)
= ar(ΔBDC) + ar(ΔDCE)
| Adding ar(ΔDCE) to both sides ⇒ ar(ACED) = ar(BDE)
⇒ ar(BDE) = ar(ACED)
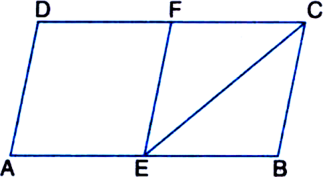
In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)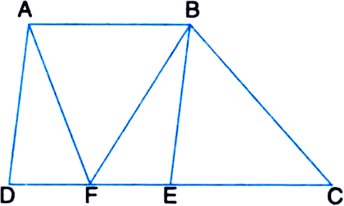
Given: ABCD is a parallelogram in which DE = EC To Prove: area (ABF) = area (BEC)
Proof: AB = DE
| Opposite sides of a parallelogram DE = EC | Given
∴ AB = EC Also, AB || DE
| Opposite sides of a parallelogram ⇒ AB || DC
Now, ΔABF and ΔBEC are on equal bases AB and EC and between the same parallels AB and DC
∴ ar(ΔABF) = ar(ΔBEC)
Areas of triangles on the same bases and between the same parallels are equal in. Prove it.
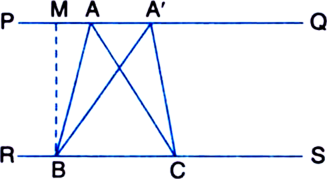
Draw BM ⊥ PQ. Then,
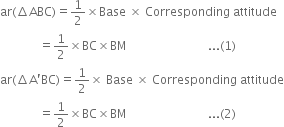
From (1) and (2), we get
ar(AABC) = ar(ΔA'BC)
Hence, ΔABC and ΔA'BC are equal in area.
Prove that the area of a trapezium is equal to half of the product of its height and sum of parallel sides.
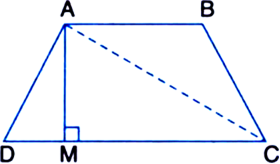
To Prove: ar(trapezium ABCD)
Construction: Join AC Proof: ar(trapezium ABCD)
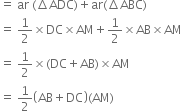
Sponsor Area
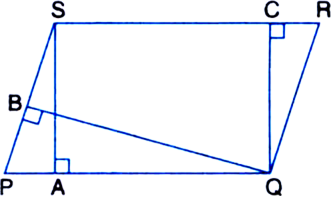
In the figure, PQRS is a parallelogram with PQ = 12 cm, altitudes corresponding to PQ and SP are respectively 8 cm and 10 cm. Find SP.
Solution not provided.
Ans. 9.6 cm
In a parallelogram ABCD, AB = 8 cm. The altitudes corresponding to sides AB and AD are respectively 4 cm and 5 cm. Find measure of AD.
Solution not provided.
Ans. 6.4 cm
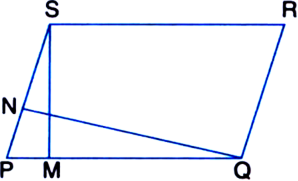
In the given figure:
(a) name the two triangles on the same base AB and between the same parallels.
(b) name a triangle and a parallelogram on the same base BC and between the same parallels.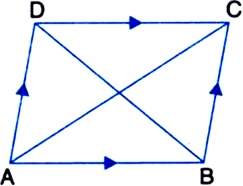
Solution not provided.
Ans. (a) ΔDAB, DCAB
(b) ΔDAB, 11 gm ABCD
In the given figure, ABC and DBC are triangles on the same base and between parallel lines l and m. If AB = 3 cm, BC = 5 cm, ∠A = 90°, find area of ΔDBC.
Solution not provided.
Ans. 7.5 cm2
In the figure, ar (ΔABE) = 50 cm2. Find the area of the parallelogram ABCD. Give reasons.
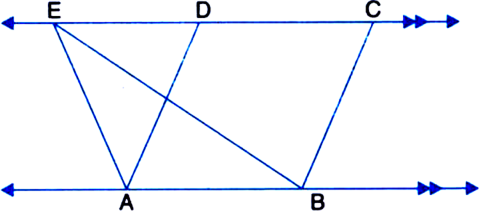
Solution not provided.
Ans. 100 cm2
If the area of parallelogram (shown in figure) is 80 cm2, then find area of ΔADP.
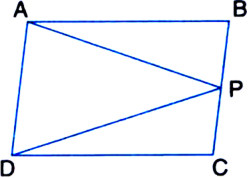
Solution not provided.
Ans. 40 cm2
In the figure, ABP is a line and BD || PC. Prove that ar(quad. ABCD) = ar(ΔAPD)
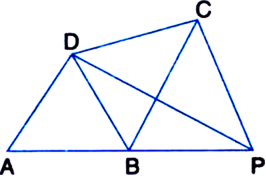
Solution not provided.
In the figure, PQRS and EFRS are two parallelograms. Show that area of  area of parallelogram PQRS.
area of parallelogram PQRS.
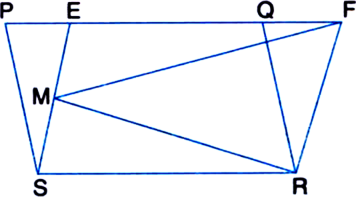

Solution not provided.
In the figure, ABCD is a parallelogram. AB = 12 cm, DM = 6 cm and BN = 9 cm. Find the length of AD.

Solution not provided.
Ans. 8 cm
In the figure, ABCD is a parallelogram. P is a point on AB produced and DN ⊥ AB. If AB = 8 cm and DN = 3 cm. Find the area of ΔCPD.
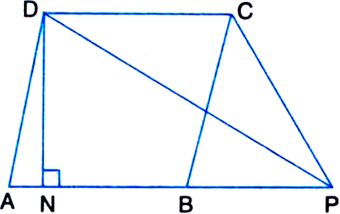
Solution not provided.
Ans. 12 cm2
ABCD is a parallelogram in which BC is produced to E such that CE = BC (see figure). AE intersects CD at F. Prove that ar(ΔBFC) 
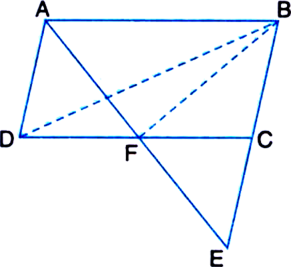
Solution not provided.
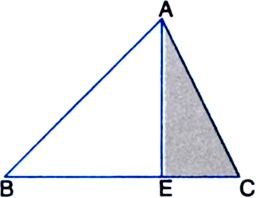
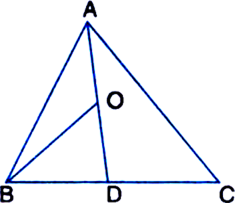
In figure, E is any point on median AD of a ΔABC. Show that ar(ΔABE) = ar(ΔACE).
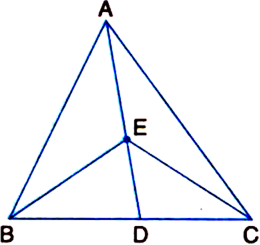
Given: E is any point on median AD of a ΔABC.
To Prove: ar(ΔABE) = ar(ΔACE).
Proof: In ΔABC,
∵ AD is a median. ∴ ar(ΔABD) = ar(ΔACD) ...(1)
∵ A median of a triangle divides it into two triangles of equal areas
In ΔEBC,
∵ ED is a median.
∴ ar(ΔEBD) = ar(ΔECD) ...(2)
∵ A median of a triangle divides it into two triangles of equal areas Subtracting (2) from (1), we get ar(ΔABD) – ar(ΔEBD)
= ar(ΔACD) – ar(ΔECD)
⇒ ar(ΔABE) = ar(ΔACE).
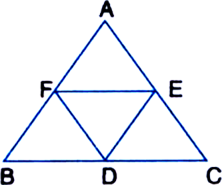
In a triangle ABC, E is the midpoint of median AD. Show that 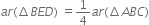
Proof: In ΔABC,
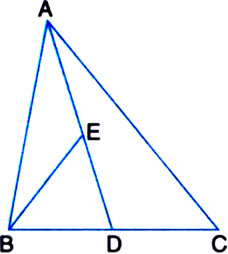
∵ AD is a median.
(1)
∵ A median of a triangle divides it into two triangles of equal areas.
In ΔABD,
∵ BE is a median.
∵ A median of a triangle divides it into two triangles of equal areas

Show that the diagonals of a parallelogram divide it into four triangles of equal area.
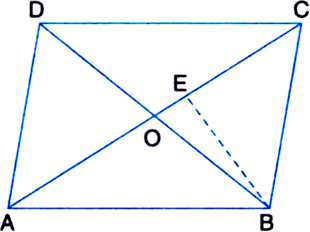
To Prove: ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA). Construction: Draw BE ⊥ AC.
Proof: ∵ ABCD is a parallelogram ∴ OA = OC and OB = OD
| ∵ Diagonals of a parallelogram bisect each other
Now,

But OA = OC
∴ ar(ΔOAB) = ar(ΔOBC) ...(1)
Similarly,
ar(ΔOBC) = ar(ΔOCD) ...(2)
and, ar(ΔOCD) = ar(ΔODA) ...(3)
From (1), (2) and (3), ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA).
In figure, ABC and ABD are two triangles on the same base AB. If line-segment CD is bisected by AB at O. Show that ar(AABC) = ar(ΔABD).
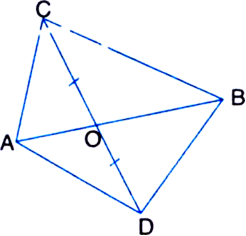
Given: ABC and ABD are two triangles on the same base AB. Line segment CD is bisected by AB at O.
To Prove: ar(ΔABC) = ar(ΔABD).
Proof: ∵ Line segment CD is bisected by AB
at O.
∴ OC = OD BO is a median of ΔBCD and AO is a median of ΔACD
∵ BO is a median of ΔBCD
∴ ar(ΔOBC) = ar(ΔOBD) ...(1)
∵ A median of a triangle divides it into two triangles of equal areas
∵ AO is a median of ΔACD
∴ ar(ΔOAC) = ar(ΔOAD) ...(2)
∵ A median of a triangle divides it into two triangles of equal areas
Adding (1) and (2), we get ar(ΔOBC) + ar(ΔOAC)
= ar(ΔOBD) + ar(ΔOAD)
⇒ ar(ΔABC) = ar(ΔABD).
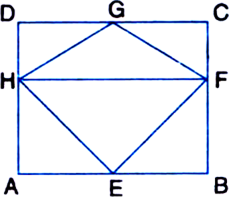
D, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC. Show that:
(i) BDEF is a parallelogram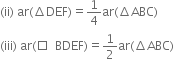
Given: D, E and F are respectively the midpoints of the sides BC, CA and AB of a ΔABC.
To Prove: (i) □BDEF is a parallelogram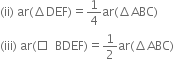
Proof: (i) In ΔABC,
∵ F is the mid-point of side AB and
E is the mid-point of side AC.
∴ EF || BC
∵ In a triangle, the line segment joining the mid-points of any two sides is parallel to the third side.
⇒ EF || BD ...(1)
Similarly, ED || BF ...(2)
In view of (1) and (2),
□ BDEF is a parallelogram.
∵ A quadrilateral is a parallelogram
if its opposite sides are parallel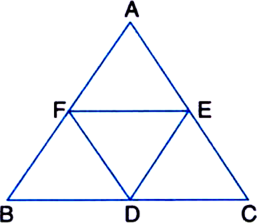
(ii) As in (i), we can prove that
□AFDE and □FDCE are parallelograms.
∵ FD is a diagonal of || gm BDEF.
ar(ΔFBD) = ar(ΔDEF) ...(3) Similarly, ar(ΔDEF) = ar(ΔFAE) ...(4) and, ar(ΔDEF) = ar(ΔDCE) ...(5)
From (3), (4) and (5), we have ar(ΔFBD) = ar(ΔDEF)
= ar(ΔFAE) = ar(ΔDCE) ...(6)
∵ ΔABC is divided into four non-overlapping triangles ΔFBD, ΔDEF, ΔFAE and ΔDCE.
∴ ar(ΔABC) = ar(ΔFBD) + ar(ΔDEF) + ar(ΔFAE) + ar(ΔDCE) = 4 ar(ΔDEF) | From (6)
⇒ ar(ΔDEF) = 1/2 ar(ΔABC). ...(7)
4
(iii) ar(□BDEF)
= ar(ΔFBD) + ar(ΔDEF)
= ar(ΔDEF) + ar(ΔDEF)
| From (3)
= 2 ar(ΔDEF)
In figure, diagonals AC and BD of quadrilateral ABCD intersect at O such that OB = OD. If AB = CD, then show that:
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.
[Hint. From D and B, draw perpendiculars to AC.]
Given: Diagonals AC and BD of a quadrilateral ABCD intersect at O such that OB = OD. To Prove: If AB = CD, then
(i) ar(ΔDOC) = ar(ΔAOB)
(ii) ar(ΔDCB) = ar(ΔACB)
(iii) DA || CB or ABCD is a parallelogram.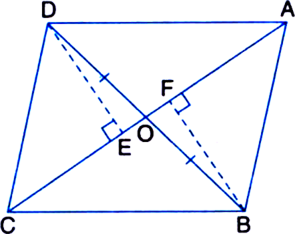
Construction: Draw DE ⊥ AC and BF ⊥ AC.
Proof: (iii) In ΔADB,
∵ AO is a median
∴ ar(ΔAOD) = ar(ΔAOB) ...(1)
∵ A median of a triangle divides it into two triangles of equal areas
In ΔCBD,
∵ CO is a median.
ar(ΔCOD) = ar(ΔCOB) ...(2)
∵ A median of a triangle divides it into two triangles of equal areas
Adding (1) and (2), we get ar(ΔAOD) + ar(ΔCOD)
= ar(ΔAOB) + ar(ΔCOB)
⇒ ar(ΔACD) = ar(ΔACB)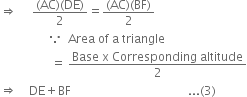
In right Δs DEC and BFA,
Hyp. DC = Hyp. BA | given
DE = BF | From (3)
∴ ΔDEC ⊥ ABFA | R.H.S. Rule
∴ ∠DCE = ∠BAF | C.P.C.T.
But these angles form a pair of equal alternate interior angles.
∴ DC || AB ...(4)
∵ DC = AB and DC || AB ∴ □ABCD is a parallelogram.
∵ A quadrilateral is a parallelogram if a pair of opposite sides are parallel and equal DA || CB
| ∵ Opposite sides of a || gm are parallel (i) ∵ ABCD is a parallelogram
∴ OC = OA ...(5)
Diagonals of a parallelogram bisect each other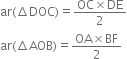
∵ DE = BF | From (3)
and OC = OA | From (5)
∴ ar(ΔDOC) = ar(ΔAOB).
(ii) From (i),
ar(ΔDOC) = ar(ΔAOB)
Δ ar(ΔDOC) + ar(ΔOCB)
= ar(ΔAOB) + ar(ΔOCB)
| Adding equal areas on both sides ⇒ ar(ΔDCB) = ar(ΔACB).
Sponsor Area
D and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC). Prove that DE || BC.
Given: D and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔEBC).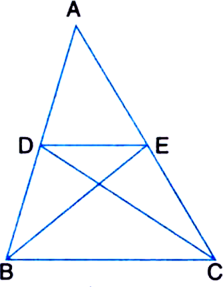
To Prove: DE || BC.
Proof: ∵ ΔDBC and ΔEBC are on the same base BC and have equal areas.
Their altitudes must be the same.
∴ DE || BC.
8. XY is a line parallel to side BC of a triangle ABC. If BE || AC and CF || AB meet XY at E and F respectively, show that ar(ΔABE) = ar(ΔACF).
Given: XY is a line parallel to side BC of a triangle ABC. BE || AC and CF || AB meet XY at E and F respectively.
To Prove: ar(ΔABE) = ar(ΔACF).
Proof: ∵ XY || BC | given
and CF || BX | ∵ CF || AB (given)
∴ □BCFX is a || gm
A quadrilateral is a parallelogram if its opposite sides are parallel
∴ BC = XF
| Opposite sides of a parallelogram are equal ⇒ BC = XY + YF ...(1)
Again,
∵ XY || BC | given
and BE || CY | ∵ BE || AC (given)
∴ □BCYE is a parallelogram
A quadrilateral is a parallelogram if its opposite sides are parallel
∴ BC = YE
| Opposite sides of a parallelogram are equal
⇒ BC = XY + XE ...(2)
From (1) and (2),
XY + YF = XY + XE
⇒ YF = XE
⇒ XE = YF ...(3)
∵ ΔAEX and ΔAYF have equal bases (∵ XE = YF) on the same line EF and have a common vertex A.
∴ Their altitudes are also the same.
∴ ar(ΔAEX) = ar(ΔAFY) ...(4)
∵ ΔBEX and ΔCFY have equal bases (∵ XE = YF) on the same line EF and are between the same parallels EF and BC (∵ XY || BC).
∴ ar(ΔBEX) = ar(ΔCFY) ...(5)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
Adding the corresponding sides of (4) and (5), we get
ar(ΔAEX) + ar(ΔBEX) = ar(ΔAFY) + ar(ΔCFY)
⇒ ar(ΔABE) = ar(⇒ACF).
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar(||gm ABCD) = ar(||gm PBQR).
[Hint. Join AC and PQ. Now compare ar(ACQ) and ar(APQ)].
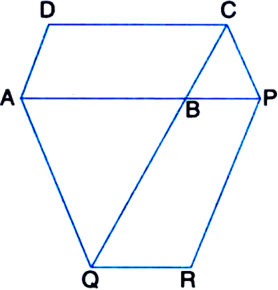
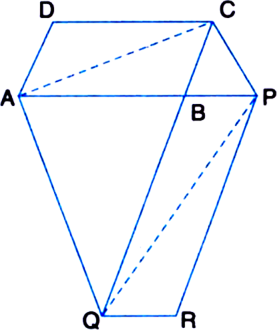
To Prove: ar(|| gm ABCD) = ar(|| gm PBQR). Construction: Join AC and PQ.
Proof: ∵ AC is a diagonal of || gm ABCD![]()
![]() PQ is a diagonal of
PQ is a diagonal of ![]() gm BQRP
gm BQRP![]()
∵ ΔACQ and ΔAPQ are on the same base AQ and between the same parallels AQ and CP. ar(ΔACQ) = ar(ΔAPQ)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area
⇒ ar(ΔACQ) – ar(ΔABQ)
= ar(ΔAPQ) – ar(ΔABQ)
| Subtracting the same areas from both sides ⇒ ar(ΔABC) = ar(ΔBPQ)![]()
| From (1) and (2)
⇒ ar(|| gm ABCD) = ar(|| gm PBQR).
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
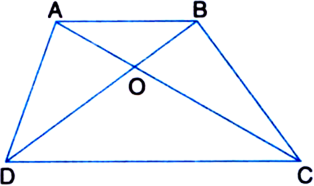
To Prove: ar(ΔAOD) = ar(ΔBOC).
Proof: ∵ ΔABD and ΔABC are on the same base AB and between the same parallels AB and DC.
∴ ar(ΔABD) = ar(ΔABC)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔABD) – ar(ΔAOB)
= ar(ΔABC) – ar(ΔAOB)
| Subtracting the same areas from both sides ⇒ ar(ΔAOD) = ar(ΔBOC).
In figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE). 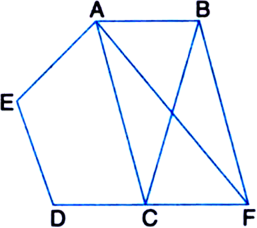
Given: ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.
To Prove: (i) ar(ΔACB) = ar(ΔACF)
(ii) ar(□AEDF) = ar(ABCDE).
Proof: (i) ∵ ΔACB and ΔACF are on the same base AC and between the same parallels AC and
BF. [∵ AC || BF (given)]
∴ ar(ΔACB) = ar(ΔACF)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
(ii) From (i),
ar(ΔACB) = ar(ΔACF)
⇒ ar(ΔACB) + ar(□AEDC)
= ar(ΔACF) + ar(□AEDC)
| Adding the same areas on both sides ⇒ ar(ABCDE) = ar(□AEDF)
⇒ ar(□AEDF) = ar(ABCDE).
A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the comers to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Let ABCD be the plot of land of the shape of a quadrilateral. Let the portion ADE be taken over by the Gram Panchayat of the village from one comer D to construct a Health Centre.
Join AC. Draw a line through D parallel to AC to meet BC produced in P. Then Itwaari must be given the land ECP adjoining his plot so as to form a triangular plot ABP as then
ar(ΔADE) = ar(ΔPEC).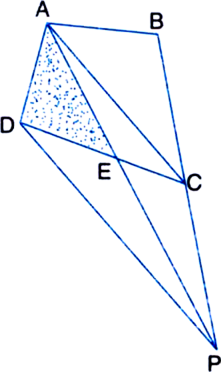
Proof: ∵ ΔDAP and ΔDCP are on the same base DP and between the same parallels DP and AC.
∴ ar(ΔDAP) = ar(ΔDCP)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
⇒ ar(ΔDAP) – ar(ΔDEP)
= ar(ΔDCP) – ar(ΔDEP)
| Subtracting the same areas from both sides
⇒ ar(ΔADE) = ar(ΔPCE)
⇒ ar(ΔDAE) + ar(□ABCE)
= ar(ΔPCE) + ar(□ABCE)
| Adding the same areas to both sides
⇒ ar(□ABCD) = ar(ΔABP).
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
[Hint. Join CX.]
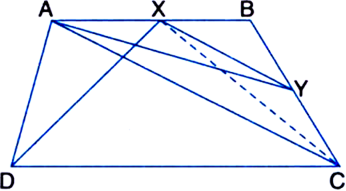
To Prove: ar(ΔADX) = ar(ΔACY).
Construction: Join CX.
Proof: ∵ ΔADX and ΔACX are on the same base AX and between the same parallels AB and DC.
∴ ar(ΔADX) = ar(ΔACX) ...(1)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ∵ ΔACX and ΔACY are on the same base AC and between the same parallels AC and XY.
∴ ar(ΔACX) = ar(ΔACY) ...(2)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area From (1) and (2), we get ar(ΔADX) = ar(ΔACY).
In figure, AP || BQ || CR. Prove that ar(ΔAQC) = ar(ΔPBR).
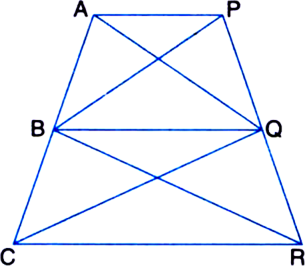
Given: AP || BQ || CR.
To Prove: ar(ΔAQC) = ar(ΔPBR).
Proof: #8757; ΔABAQ and ΔBPQ are on the same base BQ and between the same parallels BQ and AP. ∴ ar(ΔBAQ) = ar(ΔBPQ) ...(1)
V Two triangles on the same base (or equal bases) and between the
same parallels are equal in area ∵ ΔBCQ and ΔBQR are on the same base BQ and between the same parallels BQ and CR.
∴ ar(ΔBCQ) = ar(ΔBQR) ...(2)
V Two triangles on the same base (or equal bases) and between the
same parallels are equal in area Adding the corresponding sides of (1) and (2), we get
ar(ΔBAQ) + ar(ΔBCQ)
= ar(ΔBPQ) + ar(ΔBQR)
⇒ ar(ΔAQC) = ar(ΔPBR).
Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(ΔAOD) = ar(ΔBOC). Prove that ABCD is a trapezium.
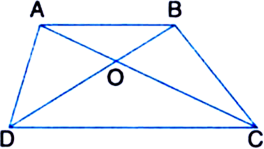
To Prove: □ABCD is a trapezium.
Proof: ar(ΔAOD) = ar(ΔBOC)
⇒ ar(ΔAOD) + ar(ΔAOB)
= ar(ΔBOC) + ar(ΔAOB)
| Adding the same areas on both sides
⇒ ar(ΔABD) = ar(ΔABC)
But ΔABD amd ΔABC are on the same base
AB.
∴ ΔABD and ΔABC will have equal corresponding altitudes.
ΔABD and ΔABC will lie between the same parallels.
∴ AB || DC
∴ [□ABCD is a trapezium.
A quadrilateral is a trapezium if exactly one pair of opposite sides is parallel
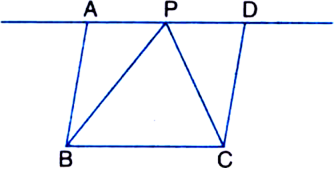
Infigure, ar(ΔDRC) = ar(ΔDPC) and ar(ΔBDP) = ar(ΔARC). Show that both the quadrilateral ABCD and DCPR are trapeziums.
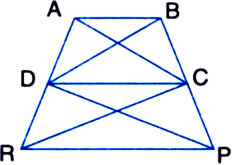
Given: ar(ΔDRC) = ar(ΔDPC) and ar(ΔBDP) = ar(ΔARC).
To Prove: Both the quadrilaterals ABCD and DCPR are trapeziums.
Proof: ar(ΔDRC) = ar(ΔDPC) ...(1)
| Given
But ΔDRC and ΔDPC are on the same base DC.
∴ ΔDRC and ΔDPC will have equal corresponding altitudes.
∴ ΔDRC and ΔDPC will lie between the same parallels.
∴ DC || RP
∴ □ DCPR is a trapezium.
A quadrilateral is a trapezium if exactly one pair of opposite sides are parallel Again. ar(ΔBDP) = ar(ΔARC)
⇒ ar(ΔBDC) + ar(ΔDPC)
= ar(ΔADC) + ar(ΔDRC)
⇒ ar(ΔBDC) = ar(ΔADC) | Using (1) But ΔBDC and ΔADC are on the same base DC.
∴ ΔBDC and ΔADC will have equal corresponding altitudes.
∴ ΔBDC and ΔADC will lie between the same parallels.
AB || DC
∴ □ABCD is a trapezium.
A quadrilateral is a trapezium if exactly one pair of opposite sides is parallel
Show that the area of a rhombus is half the product of the lengths of its diagonals.
Or
Prove that the area of a rhombus is equal to half the rectangle contained by its diagonals.
Let ABCD be a rhombus whose diagonals are AC and BD.
Then,
Area of rhombus ABCD
= Area of ΔABD + Area of ΔCBD![]()
∵ Diagonals of a rhombus are perpendiculars to each other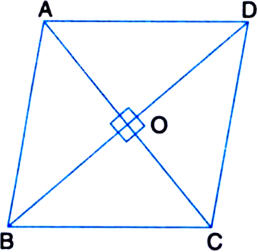
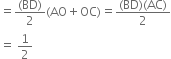
Product of the lengths of its diagonals.
Given two points A and B and a positive real number k. Find the locus of a point P such that ar(ΔPAB) = k.
Given: Two points A and B and a positive real number k.
To find: The locus of a point P such that ar(ΔPAB) = k.
Construction: Draw PM ⊥ AB.
Determination: Let PM = h
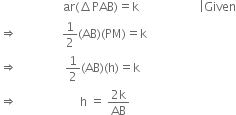
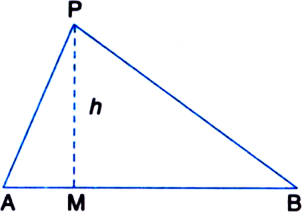
∵ Points A and B are given.
∴ AB is fixed.
Also, k being a positive real number k is fixed. ∴ h is a fixed positive real number.
∴ The locus of P is a line parallel to the line
AB at a fixed distance
Show that the line segment joining the mid-points of a pair of opposite sides of a parallelogram divides it into two equal parallelograms.
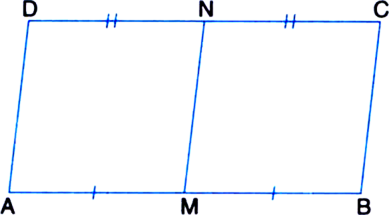
To Prove: ar(|| gm AMND) = ar(|| gm MBCN). Proof: ∵ ABCD is a || gm
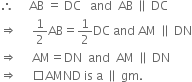
Similarly, we can prove that □MBCN is a parallelogram.
∵ || gm AMND and || gm MBCN are on equal bases AM and MB (∵ M is the mid-point of AB) and between the same parallels AB and DC.
∴ ar(|| gm AMND) = ar(|| gm MBCN).
In an equilateral triangle, O is any point is the interior of the triangle and perpendiculars are drawn from O to the sides. Prove that the sum of these perpendicular line segments is constant.
Given: ABC is an equilateral triangle. O is any point in the interior of the triangle. Perpendiculars OD, OE and OF are drawn from 0 on the sides BC, AB and AC respectively of ΔABC.
To Prove: OD + OE + OF = constant
Construction: Join O to A, B and C. Draw AH
⊥ BC.
Proof: ∵ ΔABC is an equilateral triangle AB = BC = CA![]()
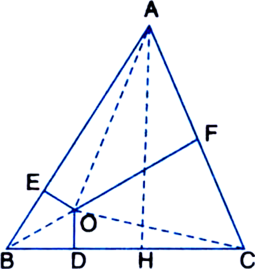
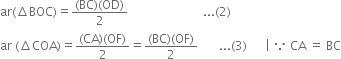
Adding (1), (2) and (3), we get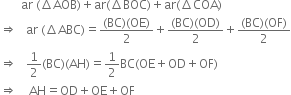
⇐ OD + OE + OF = AH which is constant for a given triangle.
ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar (ΔABC) = ar (ΔABD).
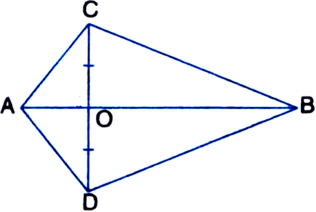
Given: ΔABC and ΔABD are two triangles on the same base AB. Line segment CD is bisected by AB at O.
To Prove: ar(ABC) = ar(ABD)
Proof: ∵ Line segment CD is bisected by AB at O
∴ CO = DO
⇒ O is the mid-point of CD.
⇒ AO is a median of ΔACD and BO is a median of ΔBCD
∵ AO is a median of ΔACD
∴ ar(ΔAOC) = ar(Δ AOD) ... (1)
∵ A median of a triangle divides it into
two triangles of equal areas
∵ BO is a median of ΔBCD ar(ΔBOC) = ar(ΔBOD) ...(2)
∵ A median of a triangle divides it into
two triangles of equal areas
Adding (1) and (2), we get ar(ΔAOC) + ar(ΔBOC)
= ar(ΔAOD) + ar(ΔBOD)
⇒ ar(ΔABC) = ar(ΔABD)
ΔABC and ΔABD are two triangles on the same base AB. If line segment CD is bisected by AB at O, show that ar (ΔABC) = ar (ΔABD).
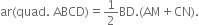
Given: BD is one of the diagonals of a quadrilateral ABCD. AM and CN are perpendiculars from A and C respectively on BD.
To Prove: ar(quad. ABCD)![]()
Proof: ar(quad ABCD)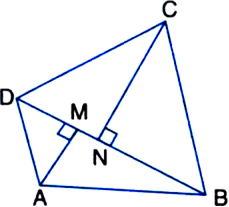
![]()
| ![]() Area of a triangle =
Area of a triangle = ![]() x Base X Corresponding altitude
x Base X Corresponding altitude![]()
ABCD is a parallelogram whose diagonals intersect at O. If P is any point on BO, prove that
(i) ar(ΔADO) = ar(ΔCDO)
(ii) ar(ΔABP) = ar(ΔCBP)
Given: ABCD is a parallelogram whose diagonals intersect at O. P is any point on BO.
To Prove:
(i) ar(ΔADO) = ar(ΔCDO) (ii) ar(ΔABP) = ar(ΔCBP)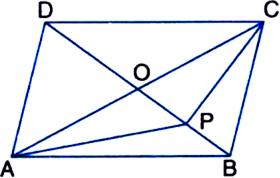
Proof:
(i) ∵ Diagonals of a parallelogram bisect each other
∴ AO = OC
⇒ O is the mid-point of AC
DO is a median of ΔDAC
ar(ΔADO) = ar(ΔCDO)
∵ A median of a triangle divides it into two triangles of equal areas
(ii) ∵ BO is a median of ΔBAC
∴ ar(ΔBOA) = ar(ΔBOC) ...(1)
∵ A median of a triangle divides it into two triangles of equal areas ∵ PO is a median of ΔPAC
∴ ar(ΔPOA) = ar(ΔPOC) ...(2)
∵ A median of a triangle divides it into two triangles of equal areas Subtracting (2) from (1), we get ar(ΔBOA) – ar(ΔPOA) = ar(ΔBOC) – ar(ΔPOC) ⇒ ar(ΔABP) = ar(ΔCBP)
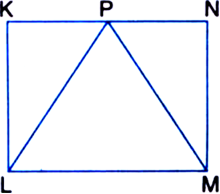
In the given figure, ΔABC is right angled at B, and BD is its median. E is the mid-point of BD. If AB = 6 cm, AC = 10 cm, calculate area of ΔBEC.
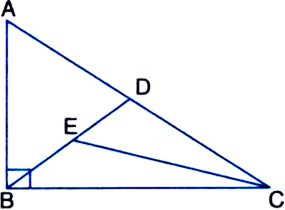
In right triangle ABC,
AB2 + BC2 = AC2
| By Pythagoras theorem ⇒ 62 + BC2 = 102
⇒ BC = 8 cm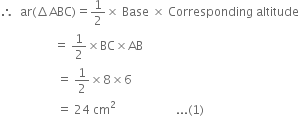
∵ BD is a median of ΔABC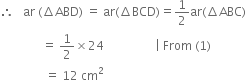
∵ A median of a triangle divides it into two triangles of equal areas ⇒ ar(ΔBCD) = 12 cm2 ...(2)
∵ E is the mid-point of BD ∴ CE is a median of ΔBCD![]()
∵ A median of a triangle divides it into two triangles of equal areas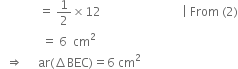
In the given figure, ΔABC is right angled at A and AD is its median. BA is produced to E such that BA = AE. ED is joined. If AB = 6 cm, BC = 10 cm, find ar(ΔBED).
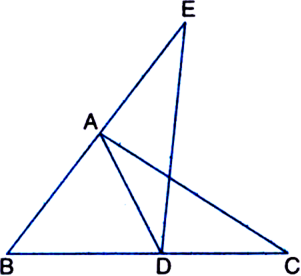
In right triangle BAC,
AB2 + AC2 = BC2
| By Pythagoras Theorem
⇒ 62 + AC2 = 102 ⇒ AC = 8 cm
∵ AD is a median of ΔABC ∴ ar(ΔABD) = ar(ΔACD)
∵ A median of a triangle divides it into two triangles of equal areas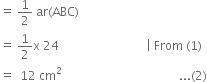
∵ BA = AE ∴ A is the mid-point of BE ∴ DA is a median of ΔBDE![]()
∵ A median of a triangle divides it into two triangles of equal areas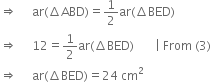
The medians of ΔABC intersect at G. Prove that
ar(ΔAGB) = ar(ΔAGC) = ar(ΔBGC) ![]()
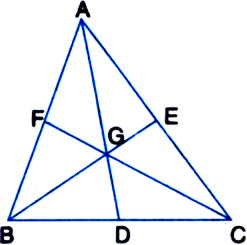
Given: The medians AD, BE and CF of ΔABC intersect at G.
To Prove: ar(ΔAGB) = ar(ΔAGC) ![]()
Proof: In ΔABC,
∵ AD is a median
∵ ar(ΔABD) = ar(ΔACD) ...(1)
A median of a triangle divides it into two triangles of equal areas
In ΔGBC,
∵ GD is a median ∴ ar(ΔGBD) = ar(ΔGCD) ...(2)
A median of a triangle divides it into two triangles of equal areas Subtracting (2) from (1), we get
ar(ΔABD) – ar(ΔGBD)
= ar(ΔACD) – ar(ΔGCD)
⇒ ar(ΔGAB) = ar(ΔGAC) ...(3)
Similarly, we can show that ar(ΔGAB) = ar(ΔGBC) ...(4)
From (3) and (4), we get ar(ΔGAB) = ar(ΔGAC) = ar(ΔGBC)
But,
ar(ΔGAB) + ar(ΔGAC) + ar(ΔGBC)
= ar(ΔABC)
⇒ 3 ar(ΔAGB) = ar(⇒ABC)
Triangles ABC and DBC are on the same base BC with vertices A and D on opposite sides of BC such that ar (ΔABC) = ar(ΔDBC). Show that BC bisects AD.
Given: Triangles ABC and DBC are on the same base BC with vertices A and D on opposite sides of BC such that ar(ΔABC) = ar(ΔDBC).
To Prove: BC bisects AD.
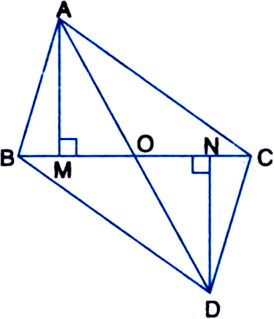
Proof: ar(ΔABC) = ar(ΔDBC) | Given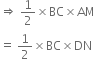
| Area of a triangle = ![]() x Base x Corresponding altitude
x Base x Corresponding altitude![]() AM = DN ...(1)
AM = DN ...(1)
In ΔAMO and ΔDNO,
AM = DN | From (1)
∠AMN = ∠DNO | Each = 90°
∠AOM = ∠DON
| Vertically opposite angles ∴ ΔAMO ⊥ ΔDNO
| AAS congruence rule ∴ AO = DO | CPCT
⇒ BC bisects AD.
Show that a median of a triangle divides it into two triangles of equal areas.
Solution not provided.
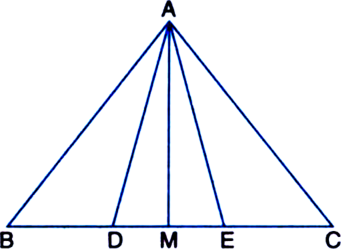
X and Y are the mid-points of the sides AB and AC respectively of a ΔABC M is any point on its base BC, Prove that 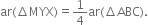
Solution not provided.
D and E are points on sides AB and AC respectively of ΔABC such that ar(ΔDBC) = ar(ΔABC). Prove that DE || BC.
Solution not provided.
In the given figure, ABCD is a parallelogram. BE⊥AD. If BE= 14 cm and AD = 8 cm, find the area of ΔDBC.
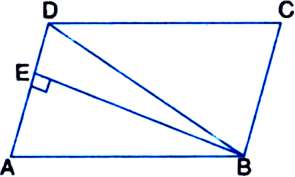
Solution not provided.
Ans. 56 cm2
In the given figure, AD is the median of ΔABC. Prove that ar(ΔABD) = art(ΔACD)
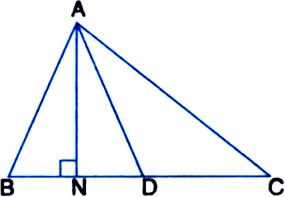
Solution not provided.
ABCD is a parallelogram with area 80 sq. cm. The diagonals AC and BD intersect at O. P is the mid-point of OA. Calculate ar(ΔBOP).
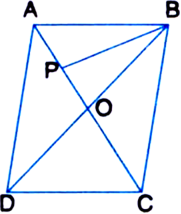
Solution not provided.
Ans. 10 cm2
D is the mid-point of side BC of ΔABC and E is the mid-point of BD. If O is the mid-point of AE, then prove that 
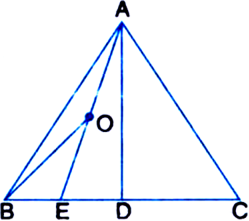
Solution not provided.
The diagonals of a quadrilateral ABCD intersect at O (see figure). Prove that if BO = OD, then ar(ΔABC) = ar(ΔADC).
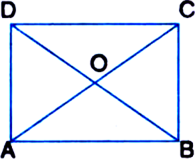
Solution not provided.
In the figure, the vertex A of ΔABC is joined to a point D on the side BC. The mid-point of AD is  .
.
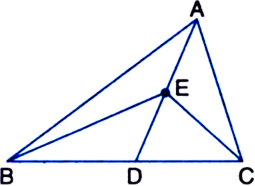
Solution not provided.
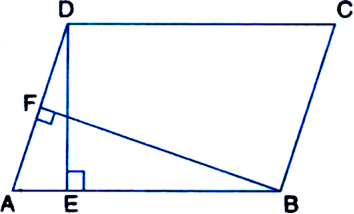
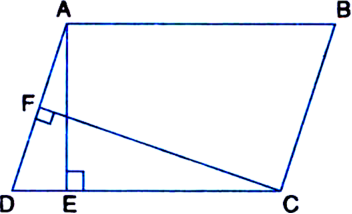
Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.
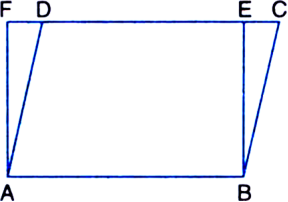
To Prove: The perimeter of the parallelogram ABCD is greater than that of rectangle ABEF.
Proof: Let ABCD be the parallelogram and ABEF be the rectangle on the same base AB and between the same parallels AB and FC. Then, perimeter of the parallelogram ABCD = 2(AB + AD) and, perimeter of the rectangle ABEF = 2(AB + AF).
In ΔADF,
∵ ∠AFD = 90°
∴ ∠ADF is an acute angle. (< 90°)
| Angle sum property of a triangle
∴ ∠AFD > ∠ADF ∴ AD > AF
Side opposite to greater angle of a triangle is longer ∴ AB + AD > AB + AF
∴ 2(AB + AD) > 2(AB + AF)
∴ Perimeter of the parallelogram ABCD > Perimeter of the rectangle ABEF.
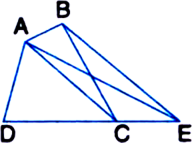
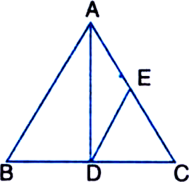
In figure, D and E are two points on BC such that BD = DE = EC. Show that ar(ΔABD) = ar(ΔADE) = ar(ΔAEC). [CBSE 2012 (March)]
Can you now answer the question that you have left in the ‘Introduction’, of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?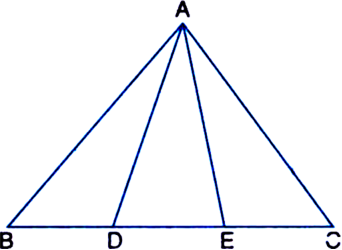
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]

∵ BD = DE = EC ∴ From (1), (2) and (3), ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
Yes, the field of Budhia has been actually divided into three parts of equal area.
In figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).

Given: ABCD, DCFE and ABFE are parallelograms.
To Prove: ar(ΔADE) = ar(ΔBCF).
Proof: ∵ ABCD is a || gm
∴ AB || DC ...(1)
| Opposite sides of a || gm are ||
∵ DCFE is a || gm
∴ DC || EF ...(2)
| Opposite sides of a || gm are ||
From (1) and (2),
AB || EF ...(3)
∵ ABCD is a || gm
∴ AD = BC ...(4)
| Opposite sides of a || gm are equal
∵ ΔADE and ΔBCF are on equal bases (∵ AD = BC) and between the same parallels AB and EF.
□∴ ar(ΔADE) = ar(ΔBCF).
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in areas
In figure, ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. If AQ intersect DC at P, show that ar(ΔBPC) = ar(ΔDPQ).
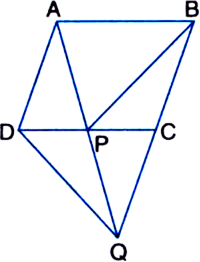
[Hint. Join AC.]
Given: ABCD is a parallelogram and BC is produced to a point Q such that AD = CQ. AQ intersects DC at P.
To Prove: ar(ΔBPC) = ar(ΔDPQ).
Construction: Join AC.
Proof: ∵ ΔQAC and ΔQDC are on the same base QC and between the same parallels AD and QC.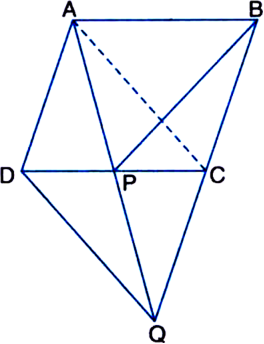
∴ ar(ΔQAC) = ar(ΔQDC) ...(1)
Two triangles on the same base (or equal bases) and between the same parallels are equal in areas
⇒ ar(ΔQAC) – ar(ΔQPC)
= ar(ΔQDC) – ar(ΔQPC)
| Subtracting the same areas from both sides
⇒ ar(ΔPAC) = ar(ΔQDP) ...(2)
∵ ΔPAC and ∵PBC are on the same base PC and between the same parallels AB and DC.
∵ ar(∵PAC) = ar(∵PBC) ...(3)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area
From (2) and (3),
ar(ΔPBC) = ar(ΔQDP)
⇒ ar(ΔBPC) = ar(ΔDPQ).
In figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that:
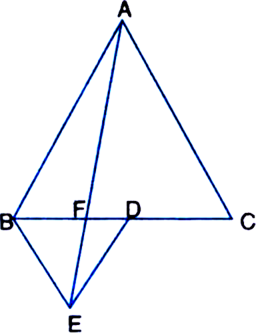
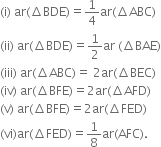
Given: ABC and BDE are two equilateral triangles such that D is the mid-point of BC. AE intersects BC at F.![]()
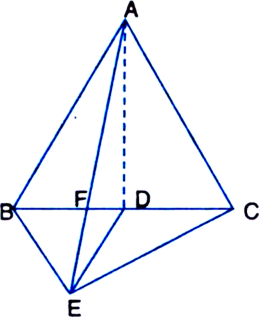
Proof: ∵ ΔABC is an equilateral triangle. ∴ ∠ABC = ∠BCA = ∠CAB = 60° ...(1)
∵ ΔBDE is an equilateral triangle.
∴ ∠BDE = ∠DEB = ∠EBD = 60° ...(2) ∠ABE + ∠BED
= ∠ABD + ∠EBD + ∠BED = 60°+ 60°+ 60°= 180°
∴ AB || DE ...(3)
∵ Sum of consecutive interior angles on
the same side of a transversal is 180° ∠EBA + ∠BAC
= ∠EBD + ∠DBA + ∠BAC = 60° + 60° + 60° = 180°
∴ AC || BE ...(4)
∵ Sum of consecutive interior angles on the same side of the transversal is 180°
∵ ΔCBA and ΔCEA are on the same base AC and between the same parallels.
∴ ar(ΔCBA) = ar(ΔCEA)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔABC) = ar(ΔCDA) + ar(ΔCED) + ar(ΔADE) ...(5)
In ΔABC,
∵ AD is a median.
![]()
∵ A median of a triangle divides it into two triangles of equal area
In ΔEBC,
∵ ED is a median.![]()
∵ A median of a triangle divides it into two triangles of equal area ∵ ΔDEA and ΔDBE are on the same base DE and between the same parallels AB and DE.
∴ ar(ΔDEA) = ar(ΔDBE) ...(8)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area
Using (6), (7) and (8), (5) gives
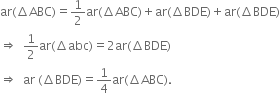
(ii) ∵ ΔBAE and ΔBCE are on the same base BE and between the same parallels BE and AC.
∴ ar(ΔBAE) = ar(ΔBCE)
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in
area
⇒ ar(ΔBAE) = 2 ar(ΔBDE)
| From (7)
![]()
(iii) 2 ar(ΔBEC) = 2.2 ar(ΔBDE)
| From (7)
= 4 ar(ΔBDE) = ar(ΔABC).
| Form (i)
(iv) ∵ ΔEBO and ΔEAD are on the same base ED and between the same parallels AB and DE.
∴ ar(ΔEBD) = ar(ΔEAD).
∵ Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔEBD) – ar(ΔEFD)
= ar(ΔEAD) – ar(ΔEFD)
| Subtracting the same areas from both sides ⇒ ar(ΔBFE) = ar(ΔAFD).
∵ Bases of ΔBDE and ΔABD are the same.![]()
ar (ΔBEF) = ar(ΔAFD) ...(10) | From (iv)![]() Altuitude of
Altuitude of ![]() Altitude of
Altitude of ![]() | From (9)
| From (9)![]() Altitude of
Altitude of ![]() Altitude of
Altitude of ![]()
From (10) and (11),
BF = 2FD ...(12)
In ΔBFE and ΔFED,
∵ BF = 2FD and, alt (ΔBFE) = alt (ΔFED) ar(ΔBFE) = 2 ar(ΔFED).
(vi) Let the altitude of ΔABD be h.
Then, altitude of ![]()
![]()
Now, ![]()
From (13) and (14), we obtain,
![]()
Diagonals AC and BD of a quadrilateral ABCD intersect each other at P. Show that ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).
[Hint From A and C, draw perpendiculars to DD.]
Given: Diagonals AC and BD of a quadrilateral ABCD intersect each other at P.
To Prove: ar(ΔAPB) x ar(ΔCPD) = ar(ΔAPD) x ar(ΔBPC).
Construction: From A and C, draw perpendiculars AE and CF respectively to BD.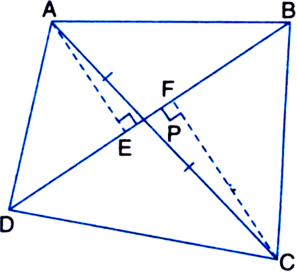
Proof: ar(AAPB) x ar(ACPD)
From (1) and (2),
ar(ΔAPB) x ar(ΔCPD)
= ar(ΔAPD) x ar(ΔBPC).
P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the mid-point of AP. Show that:
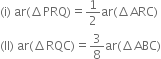
(iii) ar(ΔPBQ) = ar(ΔARC).
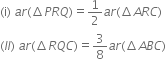
(iii) ar(ΔPBQ) = ar(ΔARC). Construction: Join AQ and CP.
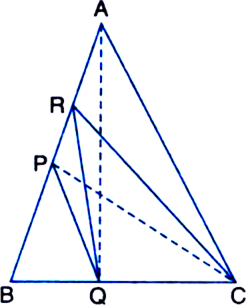
Proof: (i) ar(ΔPRQ) = ar(ΔARQ)
(∵ a median of a A divides it into triangles of equal area)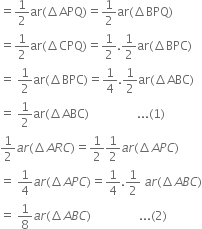
From (1) and (2), we have![]()
(ii) ar(ΔRQC) = ar(ΔRBQ) (Δ a median of a A divides it into triangles of equal areas) = ar(ΔPRQ) + ar(ΔBPQ)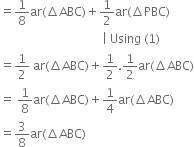
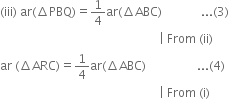
From (3) and (4),
ar(ΔPBQ) = ar(ΔARC).
Sponsor Area
In figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:
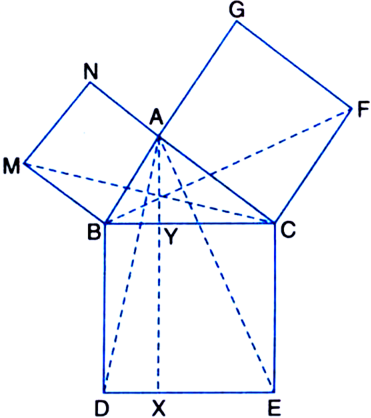
(i) ΔMBC ≅ ΔABD
(ii) ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ΔABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(ΔFCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG).
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.
Given: In figure, ABC is a right angle triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y.
To Prove: (i) ΔMBC ≅ ΔABD (ii) ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ABMN)
(iv) ΔFCB ≅ ΔACE
(v) ar(CYXE) = 2 ar(ΔFCB)
(vi) ar(CYXE) = ar(ACFG)
(vii) ar(BCED) = ar(ABMN) + ar(ACFG) Proof: (i) In ΔMBC and ΔABD,
MB = AB ...(1)
| Sides of a square BC = BD ...(2)
| Sides of a square ∠MBA = ∠CBD | Each = 90°
⇒ ∠MBA + ∠ABC = ∠CBD + ∠ABC
[adding ∠ABC to both sides] ⇒ ∠MBC = ∠ABD ...(3)
In view of (1), (2) and (3),
ΔMBC = ΔABD.
| By Congruence SAS Rule
(ii) ar(BYXD) = 2 ar(ΔABD)
⇒ ar(BYXD) = 2 ar(ΔMBC).
(iii) ar(BYXD) = 2ar(ΔABD) ar(ABMN) = 2ar(ΔMBC) = 2ar(ΔABD)
| From (i)
∴ ar(BYXD) = ar(ABMN).
(iv) In ΔFCB and ΔACE,
FC = AC | Sides of a square
CB = CE | Sides of a square
∠FCA = ∠BCE | Each = 90°
⇒ ∠FCA + ∠ACB = ∠BCE + ∠ACB
(Adding the same on both sides) ⇒ ∠FCB = ∠ACE ∴ ΔFCB ≅ ΔACE.
| SAS Congruence Rule
(v) ar(CYXE) = 2ar(ΔACE) = 2ar(ΔFCB)
| From (iv) ∵ ΔFCB ≅ ΔACE ∴ ar(ΔFCB) = ar(ΔACE) Congruent As have equal areas
(vi) ar(CYXE) = 2ar(ΔACE) = 2ar(ΔFCB) ar(ACFG) = 2ar(ΔFCB) ∴ ar(CYXE) = ar(ACFG).
(vii) ar(BCED) = ar(CYXE) + ar(BYXD)
= ar(ACFG) + ar(ABMN) = ar(ABMN) + ar(ACFG).
In figure, if AD is a median of ΔABC, then

-
ar(ΔABD) = ar(ΔADC)
-
ar(ΔABD) > ar(ΔADC)
-
ar(ΔABD) < ar(ΔADC)
-
ar(ΔABD) = 1/3 ar(ΔABC)
A.
ar(ΔABD) = ar(ΔADC)Sponsor Area
Mock Test Series
Sponsor Area
Sponsor Area