Question
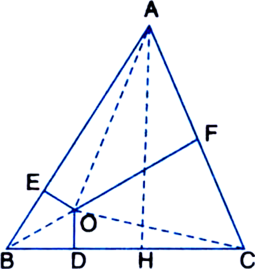
In an equilateral triangle, O is any point is the interior of the triangle and perpendiculars are drawn from O to the sides. Prove that the sum of these perpendicular line segments is constant.
Solution
Given: ABC is an equilateral triangle. O is any point in the interior of the triangle. Perpendiculars OD, OE and OF are drawn from 0 on the sides BC, AB and AC respectively of ΔABC.
To Prove: OD + OE + OF = constant
Construction: Join O to A, B and C. Draw AH
⊥ BC.
Proof: ∵ ΔABC is an equilateral triangle AB = BC = CA![]()
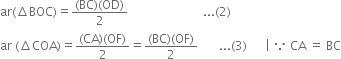
Adding (1), (2) and (3), we get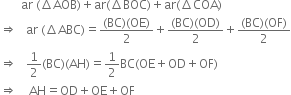
⇐ OD + OE + OF = AH which is constant for a given triangle.