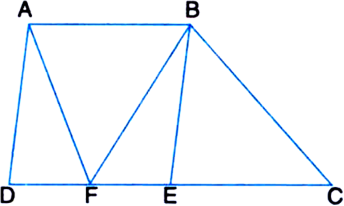
In figure, D and E are two points on BC such that BD = DE = EC. Show that ar(ΔABD) = ar(ΔADE) = ar(ΔAEC). [CBSE 2012 (March)]
Can you now answer the question that you have left in the ‘Introduction’, of this chapter, whether the field of Budhia has been actually divided into three parts of equal area?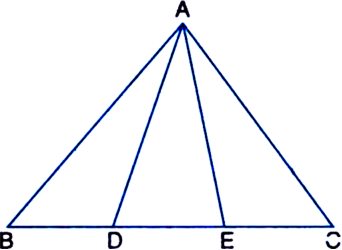
[Remark: Note that by taking BD = DE = EC, the triangle ABC is divided into three triangles ABD, ADE and AEC of equal areas. In the same way, by dividing BC into n equal parts and joining the points of division so obtained to the opposite vertex of BC, you can divide ΔABC into n triangles of equal areas.]
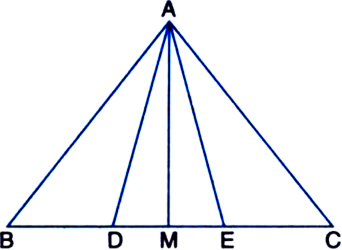

∵ BD = DE = EC ∴ From (1), (2) and (3), ar (ΔABD) = ar (ΔADE) = ar (ΔAEC)
Yes, the field of Budhia has been actually divided into three parts of equal area.