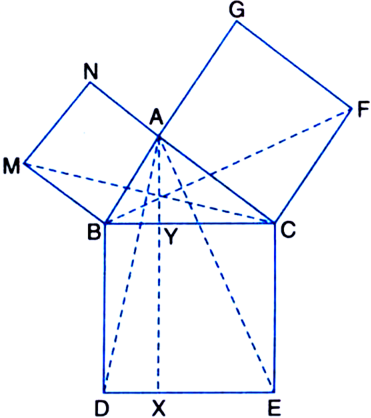
In figure, ABC is a right triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y. Show that:

(i)    ΔMBC ≅ ΔABD
(ii)    ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ΔABMN)
(iv)    ΔFCB ≅ ΔACE
(v)    ar(CYXE) = 2 ar(ΔFCB)
(vi)    ar(CYXE) = ar(ACFG)
(vii)    ar(BCED) = ar(ABMN) + ar(ACFG).
Note: Result (vii) is the famous Theorem of Pythagoras. You shall learn a simpler proof of this theorem in Class X.

Given: In figure, ABC is a right angle triangle right angled at A. BCED, ACFG and ABMN are squares on the sides BC, CA and AB respectively. Line segment AX ⊥ DE meets BC at Y.
To Prove: (i) ΔMBC ≅ ΔABD (ii) ar(BYXD) = 2 ar(ΔMBC)
(iii) ar(BYXD) = ar(ABMN)
(iv)    ΔFCB ≅ ΔACE
(v)    ar(CYXE) = 2 ar(ΔFCB)
(vi)    ar(CYXE) = ar(ACFG)
(vii)    ar(BCED) = ar(ABMN) + ar(ACFG) Proof: (i) In ΔMBC and ΔABD,
MB = AB    ...(1)
| Sides of a square BC = BD    ...(2)
| Sides of a square ∠MBA = ∠CBD    | Each = 90°
⇒ ∠MBA + ∠ABC = ∠CBD + ∠ABC
[adding ∠ABC to both sides] ⇒ ∠MBC = ∠ABD    ...(3)
In view of (1), (2) and (3),
ΔMBC = ΔABD.
| By Congruence SAS Rule
(ii)    ar(BYXD) = 2 ar(ΔABD)
⇒ ar(BYXD) = 2 ar(ΔMBC).
(iii)    ar(BYXD) = 2ar(ΔABD) ar(ABMN) = 2ar(ΔMBC) = 2ar(ΔABD)
| From (i)
∴ ar(BYXD) = ar(ABMN).
(iv)    In ΔFCB and ΔACE,
FC = AC    | Sides of a square
CB = CE    | Sides of a square
∠FCA = ∠BCE    | Each = 90°
⇒ ∠FCA + ∠ACB = ∠BCE + ∠ACB
(Adding the same on both sides) ⇒ ∠FCB = ∠ACE ∴ ΔFCB ≅ ΔACE.
| SAS Congruence Rule
(v)    ar(CYXE) = 2ar(ΔACE) = 2ar(ΔFCB)
| From (iv) ∵ ΔFCB ≅ ΔACE ∴ ar(ΔFCB) = ar(ΔACE) Congruent As have equal areas
(vi) ar(CYXE) = 2ar(ΔACE) = 2ar(ΔFCB) ar(ACFG) = 2ar(ΔFCB) ∴ ar(CYXE) = ar(ACFG).
(vii) ar(BCED) = ar(CYXE) + ar(BYXD)
= ar(ACFG) + ar(ABMN) = ar(ABMN) + ar(ACFG).