Question
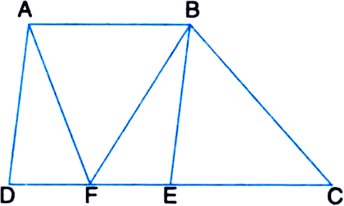
In a triangle ABC, E is the midpoint of median AD. Show that 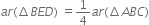
Solution
Given: In a triangle ABC, E is the midpoint of median AD.

Proof: In ΔABC,
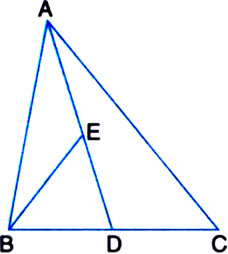
∵ AD is a median.


∵ A median of a triangle divides it into two triangles of equal areas

Proof: In ΔABC,

∵ AD is a median.
(1)
∵ A median of a triangle divides it into two triangles of equal areas.
In ΔABD,
∵ BE is a median.
∵ A median of a triangle divides it into two triangles of equal areas