Question
ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ΔADX) = ar(ΔACY).
[Hint. Join CX.]
Solution
Given: ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y.
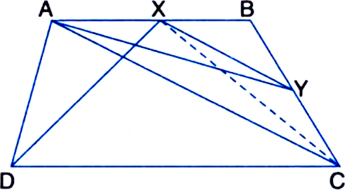

To Prove: ar(ΔADX) = ar(ΔACY).
Construction: Join CX.
Proof: ∵ ΔADX and ΔACX are on the same base AX and between the same parallels AB and DC.
∴ ar(ΔADX) = ar(ΔACX) ...(1)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ∵ ΔACX and ΔACY are on the same base AC and between the same parallels AC and XY.
∴ ar(ΔACX) = ar(ΔACY) ...(2)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area From (1) and (2), we get ar(ΔADX) = ar(ΔACY).