Question
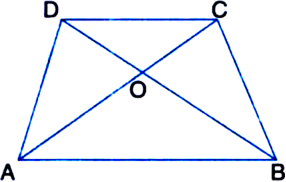
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O. Prove that ar(ΔAOD) = ar(ΔBOC).
Solution
Given: Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at O.
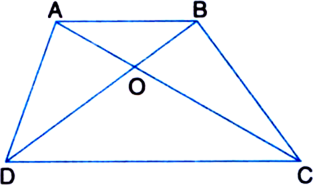

To Prove: ar(ΔAOD) = ar(ΔBOC).
Proof: ∵ ΔABD and ΔABC are on the same base AB and between the same parallels AB and DC.
∴ ar(ΔABD) = ar(ΔABC)
Two triangles on the same base (or equal bases) and between the same parallels are equal in area ⇒ ar(ΔABD) – ar(ΔAOB)
= ar(ΔABC) – ar(ΔAOB)
| Subtracting the same areas from both sides ⇒ ar(ΔAOD) = ar(ΔBOC).