Question
Given two points A and B and a positive real number k. Find the locus of a point P such that ar(ΔPAB) = k.
Solution
Given: Two points A and B and a positive real number k.
To find: The locus of a point P such that ar(ΔPAB) = k.
Construction: Draw PM ⊥ AB.
Determination: Let PM = h
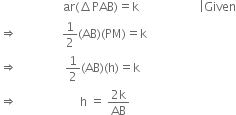
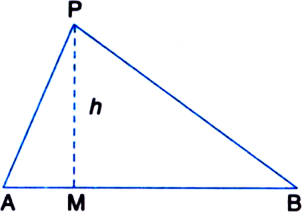
∵ Points A and B are given.
∴ AB is fixed.
Also, k being a positive real number k is fixed. ∴ h is a fixed positive real number.
∴ The locus of P is a line parallel to the line
AB at a fixed distance