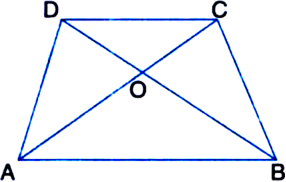
Question
P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the mid-point of AP. Show that:
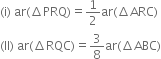
(iii) ar(ΔPBQ) = ar(ΔARC).
Solution
Given: P and Q are respectively the midpoints of sides AB and BC of a triangle ABC and R is the mid-point of AP.
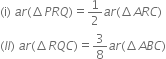
(iii) ar(ΔPBQ) = ar(ΔARC). Construction: Join AQ and CP.
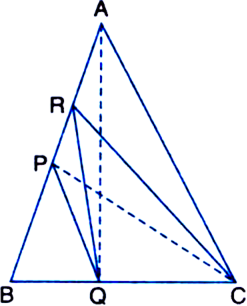
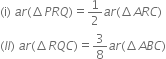
(iii) ar(ΔPBQ) = ar(ΔARC). Construction: Join AQ and CP.

Proof: (i) ar(ΔPRQ) = ar(ΔARQ)
(∵ a median of a A divides it into triangles of equal area)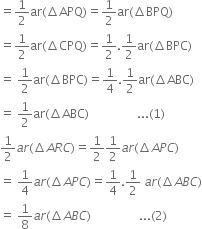
From (1) and (2), we have![]()
(ii) ar(ΔRQC) = ar(ΔRBQ) (Δ a median of a A divides it into triangles of equal areas) = ar(ΔPRQ) + ar(ΔBPQ)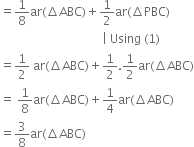
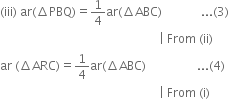
From (3) and (4),
ar(ΔPBQ) = ar(ΔARC).