Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Solution

Given: Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas.

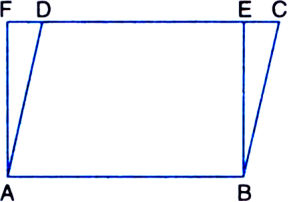
To Prove: The perimeter of the parallelogram ABCD is greater than that of rectangle ABEF.
Proof: Let ABCD be the parallelogram and ABEF be the rectangle on the same base AB and between the same parallels AB and FC. Then, perimeter of the parallelogram ABCD = 2(AB + AD) and, perimeter of the rectangle ABEF = 2(AB + AF).

In ΔADF,
∵ ∠AFD = 90°
∴ ∠ADF is an acute angle. (< 90°)
| Angle sum property of a triangle
∴ ∠AFD > ∠ADF ∴ AD > AF
Side opposite to greater angle of a triangle is longer ∴ AB + AD > AB + AF
∴ 2(AB + AD) > 2(AB + AF)
∴ Perimeter of the parallelogram ABCD > Perimeter of the rectangle ABEF.

Some More Questions From Constructions Chapter

For Daily Free Study Material Join wiredfaculty

Constructions

Parallelogram ABCD and rectangle ABEF are on the same base AB and have equal areas. Show that the perimeter of the parallelogram is greater than that of the rectangle.

Some More Questions From Constructions Chapter

Prove that of all parallelograms of which the sides are given, the parallelogram which is a rectangle, has the greatest area.

In the figure, diagonals AC and BD of a trapezium ABCD with AB || CD intersect each other at O. Show that ar(Δ AOD) = ar(Δ BOC).

Parallelograms on the same base and between same parallels are equal in area. Prove this.

ABCD is a quadrilateral and BD is one of its diagonals as shown in figure. Show that ABCD is a parallelogram and find its area.

In the given figure, AB | | DC. Show that ar(BDE) = ar(ACED).

In the given figure, ABED is a parallelogram in which DE = EC. Show that area (ABF) = area (BEC)

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction