Question
Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Solution
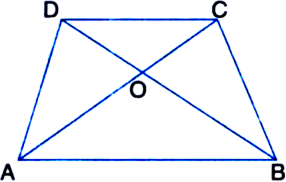
Given: ABCD is a parallelogram whose diagonals AC and BD intersecting at O divide it into four trianlges ΔOAB, ΔOBC, ΔOCD and ΔODA.
To Prove: ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA). Construction: Draw BE ⊥ AC.
Proof: ∵ ABCD is a parallelogram ∴ OA = OC and OB = OD
| ∵ Diagonals of a parallelogram bisect each other
Now,


To Prove: ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA). Construction: Draw BE ⊥ AC.
Proof: ∵ ABCD is a parallelogram ∴ OA = OC and OB = OD
| ∵ Diagonals of a parallelogram bisect each other
Now,

But OA = OC
∴ ar(ΔOAB) = ar(ΔOBC) ...(1)
Similarly,
ar(ΔOBC) = ar(ΔOCD) ...(2)
and, ar(ΔOCD) = ar(ΔODA) ...(3)
From (1), (2) and (3), ar(ΔOAB) = ar(ΔOBC)
= ar(ΔOCD) = ar(ΔODA).